MP Board Class 12th Physics Important Questions Chapter 10 तरंग-प्रकाशिकी

Students get through the MP Board Class 12th Physics Important Questions Chapter 10 तरंग-प्रकाशिकी which are most likely to be asked in the exam.

MP Board Class 12th Physics Important Questions Chapter 10 तरंग-प्रकाशिकी

अति लघु उत्तरीय प्रश्न 

प्रश्न 1.
एक तरंगाग्र के दो बिन्दुओं में कितना कलांतर होता है ?
उत्तर:
शून्य।

प्रश्न 2.
पतली फिल्म (द्रवों की सतह पर) ने रंग का कारण क्या है ?
उत्तर:
व्यतिकरण।

प्रश्न 3.
प्रकाश के व्यतिकरण के लिए किस प्रकार के स्रोतों की आवश्यकता होती है ?
उत्तर:
कला संबद्ध स्रोतों की।

प्रश्न 4.
विवर्तन प्रतिरूप प्राप्त करने के लिए स्लिट का द्वारक कितना होना चाहिए?
उत्तर:
प्रकाश के तरंगदैर्घ्य की कोटि का।

प्रश्न 5.
यंग के द्विस्लिट प्रयोग में फ्रिज चौड़ाई का सूत्र लिखिए।
उत्तर:
β = \(\frac{\mathrm{D} \lambda}{d}\)
जहाँ D स्लिट से पर्दे की दूरी, λ प्रकाश की तरंगदैर्घ्य एवं d स्लिटों से बीच की दूरी है।

प्रश्न 6.
ध्रुवण कोण पर परावर्तित किरण एवं अपवर्तित किरण के बीच कितना कोण बनता है ?
उत्तर:
90°.

प्रश्न 7.
ध्रुवण की घटना कौन-सी तरंगें प्रदर्शित करती हैं ?
उत्तर:
अनुप्रस्थ तरंगें।

प्रश्न 8.
क्रासित पोलेरॉइड का क्या अर्थ है ?
उत्तर:
उन दो पोलेरॉइडों को क्रासित पोलेरॉइड कहते हैं जिसके पारित: अक्ष परस्पर लम्बवत् होते हैं।

प्रश्न 9.
जब दूर से आते हुए प्रकाश के मार्ग में एक छोटा-सा वृत्तीय अवरोध दिया जाता है तो अवरोध की छाया के केन्द्र में चमकीला धब्बा दिखायी देता है। क्यों ? (NCERT)
उत्तर:
जब दूर से आते हुए प्रकाश के मार्ग में एक छोटा-सा वृत्तीय अवरोध रख दिया जाता है तो इसके किनारे पर प्रकाश का विवर्तन हो जाता है। विवर्तित तरंगें छाया के केन्द्र में संपोषी व्यतिकरण उत्पन्न करती है अतः केन्द्र में चमकीला धब्बा दिखायी देता है।

प्रश्न 10.
अनुदैर्ध्य तरंगों में ध्रुवण नहीं होता है। क्यों?
उत्तर:
अनुदैर्ध्य तरंगों में माध्यम के कण तरंग संचरण की ही दिशा में होते हैं अतः अनुदैर्ध्य तरंगों में ध्रुवण नहीं होता है।

लघु उत्तरीय प्रश्न

प्रश्न 1.
तरंगों के अध्यारोपण का सिद्धान्त क्या है ?
उत्तर:
अध्यारोपण का सिद्धान्त – जब दो या दो से अधिक तरंगें माध्यम के किसी बिन्दु पर एक साथ पहुँचती हैं तो परिणामी विस्थापन उन तरंगों द्वारा उत्पन्न अलग-अलग विस्थापनों के सदिश योग के बराबर होता है।

यदि n तरंगें किसी बिन्दु पर एक साथ पहुँचती हैं तथा प्रत्येक तरंग के कारण उस बिन्दु का विस्थापन क्रमशः \(\overrightarrow{y_{1}}, \overrightarrow{y_{2}}, \overrightarrow{y_{3}}\), ………… हों, तो अध्यारोपण के सिद्धान्त से उस बिन्दु का परिणामी विस्थापन
\vec{y}=\overrightarrow{y_{1}}+\overrightarrow{y_{2}}+\overrightarrow{y_{3}}+……

प्रश्न 2.
प्रकाश के व्यतिकरण से आप क्या समझते हैं ?

अथवा

प्रकाश के व्यतिकरण की परिभाषा एवं प्रकार लिखिए।
उत्तर:
प्रकाश का व्यतिकरण – जब समान आवृत्ति की दो प्रकाश तरंगें किसी माध्यम में एक ही दिशा में गमन करती हैं तो उनके अध्यारोपण के फलस्वरूप प्रकाश की तीव्रता में परिवर्तन हो जाता है। इस घटना को प्रकाश का व्यतिकरण कहते हैं।
प्रकार – व्यतिकरण दो प्रकार के होते हैं-

1. संपोषी व्यतिकरण और
2. विनाशी व्यतिकरण।

प्रश्न 3.
समझाइये कि व्यतिकरण की घटना ऊर्जा संरक्षण के नियम के अनुकूल है।

अथवा

दो तरंगों के व्यतिकरण होने में कुछ बिन्दुओं की ऊर्जा शून्य हो जाती है। क्या इस ऊर्जा का क्षय हो जाता है ?
उत्तर:
व्यतिकरण की घटना में व्यतिकरण तरंगों की कुल ऊर्जा नियत रहती है। इसमें ऊर्जा का केवल पुनर्वितरण होता है। न्यूनतम तीव्रता के स्थान पर जितनी ऊर्जा विलुप्त होती है, उतनी ही अतिरिक्त ऊर्जा अधिकतम तीव्रता के स्थान पर प्रकट हो जाती है। अत: व्यतिकरण की घटना ऊर्जा संरक्षण के नियम के अनुकूल है।

प्रश्न 4.
कला सम्बद्ध स्रोत क्या है ? दो स्रोतों के कला सम्बद्ध होने के लिए शर्ते लिखिए।
उत्तर:
कला सम्बद्ध स्रोत-ऐसे स्रोतों को कला सम्बद्ध स्रोत कहते हैं, जिनसे निकलने वाली तरंगों की आवृत्तियाँ समान होती हैं तथा कलान्तर नियत (अथवा शून्य) होता है। प्रकाश स्रोतों के कला सम्बद्ध होने के लिए निम्न शर्ते हैं-

1. दोनों स्रोतों की आवृत्तियाँ बराबर हों।
2. कलान्तर शून्य अथवा नियत हो।

प्रश्न 5.
यंग के द्विस्लिट प्रयोग में यदि एकवर्णी प्रकाश का तरंगदैर्ध्य बढ़ा दिया जाये तो फ्रिज चौड़ाई पर क्या प्रभाव पड़ेगा?
उत्तर:
सूत्र, फ्रिंज चौड़ाई β = \(\frac{\lambda D}{d}\) से स्पष्ट है कि
यदि D व d नियत हों, तो β ∝ λ
अर्थात् यदि प्रकाश का तरंगदैर्घ्य λ बढ़ा दिया जाये, तो फ्रिंज चौड़ाई β का मान बढ़ जायेगा।

प्रश्न 6.
यदि कला सम्बद्ध प्रकाश स्रोतों के बीच की दूरी कम कर दी जाये तो फ्रिंज चौड़ाई पर क्या प्रभाव पड़ेगा?
उत्तर:
फ्रिंज चौड़ाई बढ़ जायेगी। (क्योंकि β ∝ \(\frac{\mathrm{1}}{d}\) )

प्रश्न 7.
यंग के द्विस्लिट प्रयोग में यदि पर्दे को स्लिट से दूर हटाया जाये, तो क्या प्रभाव पड़ेगा?
उत्तर:
सूत्र β = \(\frac{\lambda \mathrm{D}}{d}\) से, β ∝ D.
अतः पर्दे को स्लिट से दूर हटाने पर फ्रिंज की चौड़ाई बढ़ जायेगी।

प्रश्न 8.
यंग के द्विस्लिट प्रयोग में फ्रिंज चौड़ाई पर क्या प्रभाव पड़ेगा, यदि यह प्रयोग वायु के स्थान पर जल में किया जाये ?
उत्तर:
फ्रिज चौड़ाई β = \(\frac{\lambda \mathrm{D}}{d}\) से स्पष्ट है कि यदि D और d नियत हों, तो β ∝ λ
चूँकि जल में प्रकाश का तरंगदैर्घ्य λ का मान कम हो जाता है, अत: फ्रिंज चौड़ाई β का मान कम हो जायेगा।

प्रश्न 9.
यंग के द्विस्लिट प्रयोग में व्यतिकरण फ्रेंजों पर क्या प्रभाव पड़ेगा, यदि एकवर्णी प्रकाशस्रोत श्वेत प्रकाश-स्रोत से प्रतिस्थापित किया जाता है ?

अथवा

यंग के द्विस्लिट प्रयोग में श्वेत प्रकाश का उपयोग करने पर केवल श्वेत और अदीप्त फ्रिंज प्राप्त होती हैं। क्या यह कथन सत्य है ? क्यों ?
उत्तर:
श्वेत प्रकाश सात रंगों से बना होता है। जब एकवर्णी प्रकाश-स्रोत श्वेत प्रकाश-स्रोत से प्रतिस्थापित कर दिया जाता है तो केन्द्रीय चमकीली फ्रिंज की स्थिति सभी रंगों के लिए एक ही होती है। अतः केन्द्रीय फ्रिंज श्वेत होती है। अन्य चमकीली फ्रिजों की स्थिति भिन्न-भिन्न रंगों के लिए भिन्न-भिन्न होती है। अतः अन्य फ्रिजें रंगीन बनती हैं। बैंगनी रंग का तरंगदैर्घ्य λ सबसे कम तथा लाल रंग का तरंगदैर्घ्य सबसे अधिक होता है। अत: बैंगनी रंग की फ्रिंज की कोणीय चौड़ाई सबसे कम तथा लाल रंग की प्रिंज की कोणीय चौड़ाई सबसे अधिक होती है। अत: प्रत्येक फ्रिज का वह किनारा जो केन्द्रीय फ्रिंज की ओर होता है, बैंगनी तथा दूसरा किनारा लाल दिखाई देता है।

प्रश्न 10.
यंग के द्विस्लिट प्रयोग में व्यतिकरण फ्रिंजों पर क्या प्रभाव पड़ेगा यदि इनमें से एक स्लिट को बन्द कर दिया जाये ?
उत्तर:
ऐसा करने से व्यतिकरण प्रतिरूप के स्थान पर विवर्तन प्रतिरूप प्राप्त होगा। फ्रिन्जे समदूरस्थ नहीं होंगी तथा इनकी तीव्रता क्रमशः घटती जायेगी।

प्रश्न 11.
जब नीचे उड़ता हुआ वायुयान ऊपर से गुजरता है, तो कभी-कभी टी.वी. स्क्रीन का चित्र कुछ हिलते हुए दिखाई देता है, क्यों?
उत्तर:
नीचे उड़ता हुआ वायुयान टी. वी. सिग्नल को परावर्तित कर देता है। सीधे आने वाले सिग्नल और परावर्तित सिग्नल में व्यतिकरण हो जाता है, जिससे चित्र कुछ हिलते हुए दिखाई देते है।

प्रश्न 12.
साबुन के बुलबुले रंगीन दिखाई देते हैं, क्यों?
उत्तर:
बुलबुले की ऊपरी सतह और निचली सतह से परावर्तित किरणें एक-दूसरे के साथ व्यतिकरण
करती हैं। संपोषी व्यतिकरण और विनाशी व्यतिकरण का बनना तरंगदैर्ध्य पर निर्भर करता है। श्वेत प्रकाश सात – रंगों से मिलकर बना होता है। अत: बुलबुला रंगीन दिखाई देता है।

प्रश्न 13.
प्रकाश के विवर्तन से आप क्या समझते हैं ?

अथवा

प्रकाश के विवर्तन की परिभाषा तथा प्रकार लिखिए।

अथवा

प्रकाश के विवर्तन कितने प्रकार के होते हैं ? इनके उदाहरण दीजिए। (कोई एक)
उत्तर:
जब प्रकाश किसी छोटे छिद्र से होकर गुजरता है या उसके मार्ग में कोई महीन वस्तु (अवरोध) जैसे-बाल, तार इत्यादि आ जाती है, तो प्रकाश किनारे पर मुड़ जाता है।

तीक्ष्ण धार वाले किनारों पर प्रकाश के इस प्रकार के मुड़ने की घटना को प्रकाश का विवर्तन कहते हैं।
प्रकार – विवर्तन दो प्रकार का होता है-

1. फ्रेनेल विवर्तन,
2. फ्रॉनहॉफर विवर्तन।

उदाहरण-

1. फ्रेनेल विवर्तन- ऋजुकोर द्वारा प्राप्त विवर्तन।
2. फ्रॉनहॉफर विवर्तन- एकल स्लिट द्वारा प्राप्त विवर्तन।

प्रश्न 14.
प्रकाश सरल रेखा में संचरित होता हुआ प्रतीत होता है, क्यों?
उत्तर:
क्योंकि प्रकाश का तरंगदैर्घ्य कम होता है।

प्रश्न 15.
विवर्तन प्रतिरूप प्राप्त करने के लिए स्लिट के द्वारक और तरंगदैर्ध्य में क्या सम्बन्ध होना चाहिए?
उत्तर:
स्लिट के द्वारक को प्रकाश के तरंगदैर्घ्य के क्रम का होना चाहिए।

प्रश्न 16.
ऊँचे अवरोध के दोनों ओर खड़े व्यक्ति एक-दूसरे को देख नहीं सकते किन्तु एक-दूसरे की आवाज सुन सकते हैं। क्यों ?
(NCERT)
उत्तर:
तरंगों के विवर्तन के लिए यह आवश्यक है कि अवरोध का आकार तरंग की तरंगदैर्घ्य की कोटि का होना चाहिए। ध्वनि का तरंगदैर्घ्य अवरोध के आकार का कोटि का होता है। अत: ध्वनि तरंगें विवर्तित होकर व्यक्तियों तक पहुँच जाती है और वे एक-दूसरे की आवाज सुन लेते हैं।

प्रकाश का तरंगदैर्घ्य बहुत कम होता है। जबकि अवरोध का द्वारक बहुत अधिक है अत: प्रकाश तरंगें विवर्तित नहीं हो पातीं। फलस्वरूप वे एक-दूसरे को देख नहीं पाते।

प्रश्न 17.
प्रकाश के ध्रुवण से आप क्या समझते हैं ?
उत्तर:
प्रकाश तरंग द्वारा तरंग संचरण की दिशा के चारों ओर सममिति की कमी को प्रदर्शित करना प्रकाश का ध्रुवण कहलाता है।

प्रश्न 18.
समतल ध्रुवित और अध्रुवित (सामान्य) प्रकाश में अन्तर लिखिए। (कोई दो)

अथवा

समतल ध्रुवित प्रकाश किसे कहते हैं ?
उत्तर:
समतल ध्रुवित और अध्रुवित (सामान्य) प्रकाश में अन्तर-

समतल ध्रुवित प्रकाश	अधुवित प्रकाश
1. इस प्रकाश में विद्युत् वेक्टर के कम्पन तरंग संचरण की दिशा के लम्बवत् तल में केवल एक ही दिशा में होते हैं।	इस प्रकाश में विद्युत् वेक्टर के कम्पन तरंग संचरण की दिशा के लम्बवत् तल में प्रत्येक दिशा में समान रूप से अर्थात् समरूप होते हैं ।
2. यदि इस प्रकाश को पोलेरॉइड में से गुजारा जाये तथा पोलेरॉइड को प्रकाश किरणों के परितः घुमाया जाये तो प्रकाश की तीव्रता विशेष स्थितियों में अधिकतम तथा विशेष स्थितियों में न्यूनतम होती है।	यदि इस प्रकाश को पोलेरॉइड में से गुजारा जाये तथा पोलेरॉइड को प्रकाश किरणों के परितः घुमाया जाये तो प्रकाश की तीव्रता में कोई परिवर्तन नहीं होता।

प्रश्न 19.
ध्रुवण की परिभाषा लिखिए। किस प्रकार की तरंग में ध्रुवण की घटना नहीं होती।
उत्तर:
परिभाषा के लिए लघु उत्तरीय प्रश्न 17 देखिए। अनुदैर्ध्य तरंगों में ध्रुवण की घटना नहीं होती है।

प्रश्न 20.
प्रकाश तरंगें ध्रुवित हो सकती हैं, किन्तु ध्वनि तरंगें नहीं, क्यों?

अथवा

ध्रुवण किस प्रकार की तरंगों में संभव है ?
उत्तर:
ध्रुवण की घटना केवल अनुप्रस्थ तरंगों में ही सम्भव है। प्रकाश तरंगें अनुप्रस्थ एवं ध्वनि तरंगें तरंगदैर्ध्य तरंगें होती हैं। अतः प्रकाश तरंगें ध्रुवित हो सकती हैं, ध्वनि तरंगें नहीं।

प्रश्न 21.
ध्वनि तरंगों की प्रकृति अनुप्रस्थ नहीं होती है। प्रमाण दीजिए।
उत्तर:
ध्वनि तरंगों में ध्रुवण की घटना सम्भव नहीं है। ध्रुवण की घटना केवल अनुप्रस्थ तरंगों में ही होती है, तरंगदैर्घ्य तरंगों में नहीं। इससे सिद्ध होता है कि ध्वनि तरंगों की प्रकृति अनुप्रस्थ नहीं होती।

प्रश्न 22.
व्यतिकरण और विवर्तन की परिघटनाओं से ध्रुवण की परिघटना किस प्रकार भिन्न है ?
उत्तर:
व्यतिकरण और विवर्तन की परिघटनाएँ अनुप्रस्थ और अनुदैर्ध्य दोनों प्रकार की तरंगों में होती हैं जबकि ध्रुवण की परिघटना केवल अनुप्रस्थ तरंगों में ही होती है।

प्रश्न 23.
X – किरणों, ध्वनि तरंगों और रेडियो तरंगों में किन-किन तरंगों का ध्रुवण सम्भव है और क्यों?
उत्तर:
X – किरणों और रेडियो तरंगों का ध्रुवण सम्भव है, क्योंकि ये अनुप्रस्थ तरंगें हैं।

प्रश्न 24.
ध्रुवण कोण से क्या तात्पर्य है ? किसी पारदर्शी माध्यम के लिए यह किन-किन कारकों पर निर्भर करता है ?
उत्तर:
ध्रुवण कोण – आपतन कोण के उस न्यूनतम मान को, जिसके लिए परावर्तित प्रकाश पूर्णत: ध्रुवित होता है, ध्रुवण कोण कहते हैं। किसी पारदर्शी माध्यम के लिए ध्रुवण कोण
(i) माध्यम के अपवर्तनांक और
(ii) आपतित प्रकाश के तरंगदैर्ध्य पर निर्भर करता है।

प्रश्न 25.
बुस्टर का नियम क्या है ?
उत्तर:
इस नियमानुसार, किसी माध्यम का अपवर्तनांक μ ध्रुवण कोण i_p की स्पर्शज्या (tangent) के बराबर होता है। सूत्र के रूप में, μ = tan i_p.

प्रश्न 26.
धूप के चश्मे जो पोलेरॉइड के बने होते हैं, रंगीन काँच से बने चश्मों की अपेक्षा अधिक उपयोगी होती हैं, क्यों?
उत्तर:
वस्तुओं से परावर्तित प्रकाश आंशिक समतल ध्रुवित होता है। पोलेरॉइड आंशिक ध्रुवित प्रकाश के क्षैतिज कम्पनों को काट देता है। फलस्वरूप प्रकाश की चकाचौंध समाप्त हो जाती है। रंगीन काँच से बने चश्मे प्रकाश की चकाचौंध को दूर नहीं कर पाते।

प्रश्न 27.
यंग के द्विस्लिट प्रयोग का महत्व बताइये।
उत्तर:

• यह प्रकाश के व्यतिकरण को प्रदर्शित करने वाला पहला प्रयोग था।
• इस प्रयोग से यह सिद्ध होता है कि प्रकाश तरंग के रूप में संचरित होता है। केवल प्रकाश का तरंग सिद्धान्त ही व्यतिकरण की संतोषप्रद व्याख्या कर सकता है।

प्रश्न 28.
यंग के द्विस्लिट प्रयोग में फ्रिंज की चौड़ाई किन-किन बातों पर निर्भर करती हैं, केवल नाम लिखिए।
उत्तर:
सूत्र β = \(\frac{\lambda \mathrm{D}}{d}\) के अनुसार फ्रिंज की चौड़ाई

1. प्रकाश के तरंगदैर्घ्य λ
2. कला-सम्बद्ध स्रोतों से पर्दे के बीच की दूरी D तथा
3. कला-सम्बद्ध स्रोतों के बीच की दूरी d पर निर्भर करती है।

प्रश्न 29.
साबुन के बुलबुले की पतली फिल्म पर या पानी की सतह पर तेल की बूंद की पतली फिल्म पर श्वेत प्रकाश डालने पर सुन्दर रंग दिखाई पड़ते हैं। कारण बताइए।

अथवा

साबुन का बुलबुला रंगीन दिखाई पड़ता है। कारण स्पष्ट कीजिए।
उत्तर:
जब सूर्य का प्रकाश पतली फिल्म (जिसकी मोटाई प्रकाश के तरंगदैर्घ्य की कोटि की होती है) पर आपतित होता है तो इसका कुछ भाग फिल्म के ऊपरी पृष्ठ से परावर्तित हो जाता है तथा शेष भाग उसके अन्दर प्रवेश करके निचले पृष्ठ से परावर्तित होता है। दोनों पृष्ठों से परावर्तित इन प्रकाश तरंगों में व्यतिकरण होता है । चूँकि श्वेत प्रकाश सात रंगों से बना होता है, परावर्तित तरंगों के व्यतिकरण के कारण फिल्म रंगीन दिखाई देती है।

प्रश्न 30.
तरंग प्रकाशिकी का सिद्धान्त क्या है ?

अथवा

हाइगन का तरंग सिद्धान्त क्या है ?

अथवा

प्रकाश का तरंग सिद्धान्त क्या है ?
उत्तर:
प्रकाश का तरंग सिद्धान्त-सन् 1678 में हॉलैण्ड के वैज्ञानिक क्रिश्चियन हाइगन (Christian Huyghen) ने प्रकाश संचरण से सम्बन्धित तरंग सिद्धान्त का प्रतिपादन किया था जो निम्नलिखित हैं-

• सम्पूर्ण ब्रह्माण्ड में काल्पनिक माध्यम ईथर व्याप्त है। यह भारहीन तथा समांगी होता है। इसका घनत्व बहुत ही कम तथा प्रत्यास्थता बहुत अधिक होती है।
• जब किसी स्रोत से प्रकाश ऊर्जा निकलती है तो ईथर में तरंगें उत्पन्न हो जाती हैं और इस प्रकार तरंगों के द्वारा प्रकाश का संचरण होता है।
• ये तरंगें सभी दिशाओं में अत्यधिक वेग (3 × 10⁸ मीटर/सेकण्ड) से चलती हैं।
• विभिन्न रंगों का आभास तरंगदैर्ध्य में अन्तर के कारण होता है।
• प्रारम्भ में प्रकाश तरंग को अनुदैर्ध्य माना गया था, किन्तु बाद में ध्रुवण की व्याख्या करने के लिए इसे अनुप्रस्थ माना गया।

प्रश्न 31.
पोलेरॉइड क्या है ? पोलेरॉइड का वर्णन निम्न बिन्दुओं के आधार पर कीजिए। (अ) कार्य विधि, (ब) कोई दो उपयोग।
उत्तर:
पोलेरॉइड समतल ध्रुवित प्रकाश उत्पन्न करने की एक सरल व सस्ती युक्ति है।
कार्यविधि – जब साधारण प्रकाश पोलेरॉइड पर आपातेत होता है तो उसके वे ही वैद्युत वेक्टर पोलेरॉइड में से निकल पाते हैं जिनके कम्पन क्रिस्टलों के अक्ष के समान्तर होते हैं । इस प्रकार पोलेरॉइड से निर्गत प्रकाश समतल-ध्रुवित प्रकाश होता है।

पोलेरॉइड के उपयोग – पोलेरॉइट के उपयोग निम्नलिखित हैं-

1. प्रकाश की चकाचौंध दूर करने में।
2. रात्रि के समय आमने-सामने के दो वाहनों को सुरक्षित पार करने में।
3. धातुओं के प्रकाशीय गुणों के अध्ययन में।
4. ध्रुवित प्रकाश के संसूचन में।
5. पोलेरॉइड कैमरा और फोटोग्राफी में।
6. तीन विमा वाले चित्रों को देखने में,
7. वायुयान और ट्रेन में प्रवेश करने वाले प्रकाश की तीव्रता को नियंत्रित करने में।

प्रश्न 32.
यदि ध्रुवण कोण 30° हो, तो माध्यम का अपवर्तनांक कितना होगा?
उत्तर:
ब्रुस्टर के नियम से,
माध्यम का अपवर्तनांक µ = tan i_p
या µ = tan 30°, [दिया है : i_p = 30° ]
∴ µ = \(\frac{1}{\sqrt{3}}\)

प्रश्न 33.
परिभाषित कीजिये(अ) कम्पन तल, (ब) ध्रुवण तल।
उत्तर:
(अ) कम्पन तल – कम्पन तल वह तल होता है जिसमें समतल ध्रुवित प्रकाश के विद्युत् वेक्टर …. के कम्पन और प्रकाश संचरण की दिशा स्थित होती है।

(ब) ध्रुवण तल – ध्रुवण तल वह तल होता है जो कम्पन तल के लम्बवत् होता है तथा जिसमें प्रकाश संचरण की दिशा स्थित होती है।
प्रकाश संचरण की दिशा

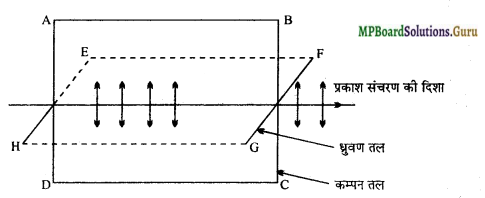
ABCD – कम्पन तल, EFGH – ध्रुवण तल।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
हाइगन का द्वितीयक तरंगिकाओं का सिद्धान्त समझाइए।
उत्तर:

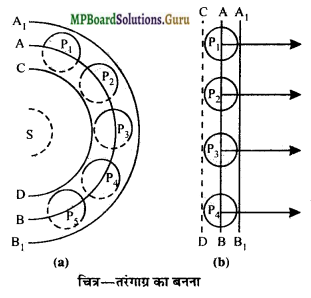
हाइगन का द्वितीयक तरंगिकाओं का सिद्धान्त-

• तरंगाग्र का प्रत्येक बिन्दु तरंग-स्रोत का कार्य करता है, जिससे नई तरंगें उत्पन्न होती हैं। इन तरंगों को द्वितीयक तरंगिकाएँ कहते हैं।
• द्वितीयक तरंगिकाएँ मूल तरंग के वेग से ही आगे बढ़ती हैं।
• किसी भी क्षण इन द्वितीयक तरंगिकाओं पर बाहर की ओर खींचा गया अन्वालोप (Envelop) उस क्षण पर नये तरंगाग्र की स्थिति को प्रदर्शित करता हैं।

मानलो S एक बिन्दु प्रकाश-स्रोत है। AB किसी क्षण पर उससे उत्पन्न गोलाकार तरंगाग्र का एक भाग है। t समय पश्चात् इस तरंगाग्र की स्थिति क्या होगी,यह ज्ञात करना है।

हाइगन के अनुसार, तरंगाग्र AB का प्रत्येक बिन्दु तरंग-स्रोत की भाँति कार्य करेगा। अत: इस तरंगाग्र AB पर कुछ बिन्दु P, P₁, P₂, P₃,P₄. … लो।

इन बिन्दुओं से उत्पन्न तरंगिकाओं के द्वारा t समय में तय की गई दूरी = νt, जहाँ ν तरंगिकाओं (अर्थात् तरंग) का वेग है।

अत: P₁, P₂, P₃, P₄,….. को केन्द्र मानकर νt त्रिज्या के गोले खींचो। इन गोलों के बाहर की ओर खींचा गया अन्वालोप या आवरण A₁B₁ नवीन तरंगाग्र को प्रदर्शित करता है। यह नवीन तरंगाग्र भी गोलाकार होगा, चित्र (a)। इसी तरह चित्र (b) में समतल तरंगाग्र का बनना प्रदर्शित किया गया है। पूर्ववर्ती तरंगाग्र AB पर द्वितीयक तरंगिकाओं के जनक बिन्दु P₁, P₂, P₃, P₄,… लिये गये हैं तथा नवीन तरंगाग्र A₁B₁ का बनना प्रदर्शित किया गया है। ध्यान रहे एक और अन्वालोप CD का निर्माण किया जा सकता है, किन्तु यह किरणों के बढ़ने की विपरीत दिशा में है। अतः इसे तरंगाग्र नहीं कहा जा सकता।

प्रश्न 2.
तरंगाग्र से आप क्या समझते हैं ? यह कितने प्रकार का होता है ?
उत्तर:
तरंगाग्र – जब किसी प्रकाश-स्रोत से प्रकाश तरंगें । निकलती हैं तो माध्यम में किसी क्षण विशेष पर वह सतह जिस पर सभी समान कला में होते हैं, तरंगाग्र कहलाती है। तरंगाग्र तीन प्रकार के होते है-
(i) गोलीय तरंगाग्र – जब प्रकाश-स्रोत, बिन्दु समान होता है तो स्रोत से सीमित दूरी पर जो तरंगाग्र बनता है, उसे गोलीय तरंगाग्र कहते हैं।

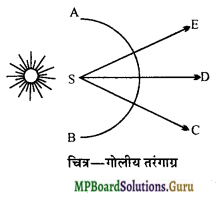
(ii) बेलनाकार तरंगाग्र – जब प्रकाश-स्रोत रेखावत् हो तो इस स्रोत से सीमित दूरी पर स्थित तरंगाग्र को बेलनाकार तरंगाग्र कहते हैं।

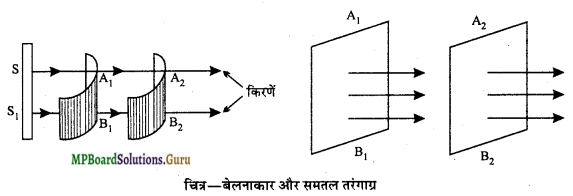
(iii) समतल तरंगाग्र – प्रकाश-स्रोत चाहे बिन्दुवत् हो या सरल रेखावत् उससे अनन्त दूरी पर स्थित तरंगाग्र को समतल तरंगाग्र कहते हैं।

प्रश्न 3.
प्रकाश का व्यतिकरण क्या है ? इसके लिए आवश्यक शर्ते लिखिए।

अथवा

प्रकाश के व्यतिकरण के लिए आवश्यक शर्ते लिखिए।
उत्तर:
प्रकाश का व्यतिकरण-लघु उत्तरीय प्रश्न क्रमांक 2 देखिए।
प्रकाश के व्यतिकरण के लिए आवश्यक शर्ते-

1. दोनों तरंगों की आवृत्तियाँ समान होनी चाहिए।
2. दोनों तरंगों के आयाम लगभग समान होने चाहिए।
3. दोनों तरंगों को एक ही दिशा में गमन करना चाहिए।
4. दोनों स्रोत एक-दूसरे के निकट हों।
5. दोनों प्रकाश-स्रोत अत्यन्त संकीर्ण हों।
6. तरंगों का कलान्तर नियत हो।
7. प्रकाश-स्रोत एकवर्णी होने चाहिए।
8. यदि प्रकाश तरंगें ध्रुवित हों, तो उनके ध्रुवण तल समान होने चाहिए।

प्रश्न 4.
प्रकाश के व्यतिकरण से आप क्या समझते हैं ? संपोषी और विनाशी व्यतिकरण को परिभाषित कर इनके लिए आवश्यक प्रतिबंध लिखिए।
उत्तर:

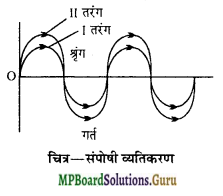
प्रकाश का व्यतिकरण – लघु उत्तरीय प्रश्न क्रमांक 2 देखिए।
संपोषी व्यतिकरण – जब समान आवृत्ति की दो तरंगें किसी बिन्दु पर समान कला में अध्यारोपित होती हैं अर्थात् जब दोनों
तरंगों के शृंग या गर्त एक साथ पड़ते हैं, तो उस बिन्दु पर परिणामी तीव्रता (अथवा आयाम) अधिकतम होती है। इस प्रकार के व्यतिकरण को संपोषी व्यतिकरण कहते हैं।

प्रतिबन्ध – दोनों तरंगों के मध्य कलान्तर शून्य अथवा π का समगुणक होना चाहिए अर्थात् दोनों तरंगों को समान
चित्र–संपोषी व्यतिकरण कला में होना चाहिए।

सूत्र के रूप में कलान्तर Φ = 2n. π, जहाँ n=0, 1, 2, 3,………..
विनाशी व्यतिकरण – जब समान आवृत्ति की दो तरंगें किसी बिन्दु पर विपरीत कला में अध्यारोपित होती हैं, अर्थात् जब एक तरंग का श्रृंग दूसरी तरंग के गर्त पर या इसके विपरीत पड़ती है, तो उस बिन्दु पर परिणामी तीव्रता (अथवा आयाम) न्यूनतम होती है। इस प्रकार के व्यतिकरण को विनाशी व्यतिकरण कहते हैं।

प्रतिबन्ध – दोनों तरंगों के मध्य कलान्तर को π का विषम गुणक होना चाहिए अर्थात् दोनों तरंगों को विपरीत कला में होना चाहिए।
सूत्र के रूप में कलान्तर Φ = (2n – 1)π , जहाँ n = 1, 2, 3, ……

प्रश्न 5.
ऋजुकोर द्वारा प्रकाश का विवर्तन किस प्रकार होता है ? तीव्रता वितरण आरेख भी बनाइए।

अथवा

ऋजुकोर द्वारा प्रकाश के विवर्तन का वर्णन निम्न बिन्दुओं के आधार पर कीजिए- …
(i) प्रायोगिक व्यवस्था,
(ii) प्रेक्षण,
(iii) तीव्रता वितरण आरेख।
उत्तर:

(i) प्रायोगिक व्यवस्था – चित्र में S एक संकीर्ण स्लिट है जो एकवर्णी प्रकाश-स्रोत से प्रदीप्त किया गया है। स्लिट S के सामने तीक्ष्ण ऋजु कोर (सीधी कोर) वाला एक अवरोध AB इस प्रकार रखा गया है कि उसकी कोर स्लिट के समान्तर रहे। अवरोध AB से कुछ दूरी पर उसके समान्तर एक पर्दा XY रखा गया है। चित्र में WW’ एक बेलनाकार तरंगाग्र है।

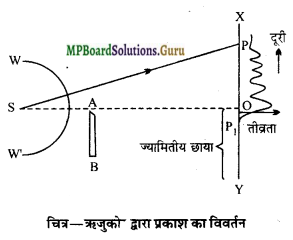
(ii) प्रेक्षण – ज्यामितीय प्रकाशिकी के अनुसार पर्दे XY के बिन्दु O के ऊपर प्रकाश की तीव्रता एकसमान होनी चाहिये, क्योंकि इस भाग में प्रकाश किरणें बिना किसी रुकावट के सीधे पहुँच जाती हैं।

बिन्दु O के नीचे ज्यामितीय छाया में पूर्णतः अन्धकार होना चाहिये, क्योंकि इस भाग में प्रकाश किरणें अवरोध AB द्वारा रोक ली जाती हैं, किन्तु ऐसा नहीं होता। वास्तव में निम्न प्रतिरूप प्राप्त होता है-

(a) ज्यामितीय छाया वाले भाग OY में भी कुछ प्रकाश पहुँच जाता है जिसकी तीव्रता तेजी से कम होती जाती है और O से कुछ ही दूरी पर बिन्दु P₁ पर तीव्रता शून्य हो जाती है। इस प्रकार बिन्दु P₁ के पश्चात् ही पूर्ण अन्धकार होता है।

(b) प्रदीप्त क्षेत्र OX में कोर की लम्बाई के समान्तर दीप्त और अदीप्त फ्रिन्जें दिखाई देती हैं। बिन्दु O के ऊपर जाने पर फ्रिन्जों की चौड़ाई कम होती जाती है, साथ-ही-साथ दीप्त फ्रिन्जों की तीव्रता घटती जाती है और अदीप्त फ्रिन्जों की तीव्रता बढ़ती जाती है। अन्त में बिन्दु P के ऊपर फ्रिन्जें समाप्त हो जाती हैं और प्रकाश की तीव्रता एकसमान दिखाई देती है।

(iii) तीव्रता वितरण आरेख – चित्र के दायीं ओर ज्यामितीय छाया और प्रदीप्त क्षेत्र में तीव्रता वितरण आरेख प्रदर्शित किया गया है।

प्रश्न 6.
प्रकाश के व्यतिकरण एवं विवर्तन में कोई चार अंतर लिखिये।
उत्तर – प्रकाश के व्यतिकरण और विवर्तन में अन्तर

व्यतिकरण	विवर्तन
1. दो कला-सम्बद्ध स्रोतों से आने वाली तरंगों के अध्यारोपण के कारण व्यतिकरण प्रतिरूप बनता है।	1. एक ही स्रोत के विभिन्न भागों से आने वाली  तरंगों के अध्यारोपण के कारण विवर्तन प्रतिरूप बनता है।
2. सभी दीप्त बैण्डों की तीव्रता एकसमान होती है।	2. केन्द्रीय उच्चिष्ठ की तीव्रता अधिकतम होती है। शेष द्वितीयक उच्चिष्ठों की तीव्रता क्रमशः घटती जाती है।
3. व्यतिकरण फ्रिजों की चौड़ाई प्रायः एकसमान होती है।	3. केन्द्रीय उच्चिष्ठ की चौड़ाई अन्य द्वितीयक उच्चिष्ठों की चौड़ाई की दुगुनी होती है।
4. न्यूनतम तीव्रता के बिन्दु पूर्णतः काले होते हैं। अतः विपर्यास अच्छा होता है।	4. न्यूनतम तीव्रता के बिन्दु पूर्णत: काले नहीं होते। अत: विपर्यास अच्छा नहीं होता।

प्रश्न 7.
प्रकाश तरंगें अनुप्रस्थ प्रकृति की होती हैं। इसे सिद्ध करने के लिए एक प्रयोग का वर्णन कीजिए।
उत्तर:
इसे सिद्ध करने के लिए दो पोलेरॉइड A और B लेते हैं। सर्वप्रथम दोनों पोलेरॉइडों को इस प्रकार रखते हैं कि उनके अक्ष परस्पर समान्तर हों।

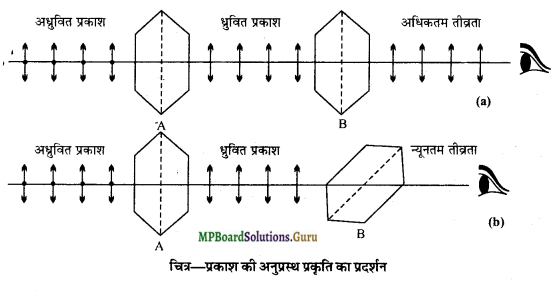
इस स्थिति में B से देखने पर निर्गत प्रकाश की तीव्रता अधिकतम होती है। अब A को स्थिर रखकर B को उसके ही तल में क्रमश: घुमाते जाते हैं। ऐसा करने से निर्गत प्रकाश की तीव्रता क्रमशः कम होने लगती है और जब पोलेरॉइट B का अक्ष पोलेरॉइड A के अक्ष के लम्बवत् हो जाता है तो निर्गत प्रकाश की तीव्रता न्यूनतम हो जाती है जिससे लगभग अँधेरा छा जाता है। इसके आगे पोलेरॉइड B को और घुमाने पर प्रकाश की तीव्रता क्रमशः बढ़ने लगती है तथा जब उसका अक्ष A के अक्ष के समान्तर हो जाता है, तो निर्गत प्रकाश की तीव्रता पनः अधिकतम हो जाती है।

इससे यह सिद्ध होता है कि प्रकाश-तरंगों में अनुप्रस्थ कम्पन होते हैं । यदि प्रकाश-तरंगों में अनुदैर्ध्य कम्पन होते तो निश्चित रूप से क्रिस्टल B को घुमाने पर प्रकाश की तीव्रता में कोई परिवर्तन नहीं होता। इस प्रकार प्रकाश-तरंग अनुप्रस्थ तरंग होती है।

प्रश्न 8.
परावर्तन द्वारा प्रकाश के ध्रुवण की घटना को समझाइए।
उत्तर:

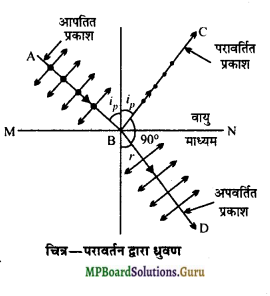
जब साधारण प्रकाश किसी पारदर्शी माध्यम जैसे – काँच आदि के पृष्ठ से परावर्तित होता है तो वह आंशिक रूप से समतल ध्रुवित हो जाता है। आपतन कोण के मान को बढ़ाने पर आपतन कोण के एक विशेष मान के लिए परावर्तित प्रकाश पूर्णतः समतल ध्रुवित हो जाता है । आपतन कोण के इस मान को ध्रुवण कोण कहते हैं।

चित्र में AB आपतित प्रकाश, BC परावर्तित प्रकाश तथा BD अपवर्तित प्रकाश है।
MN वायु और माध्यम का पृथक्कारी पृष्ठ या परावर्तक पृष्ठ है। जब प्रकाश ध्रुवण कोण i_p पर आपतित होता है, तो BC के अनुदिश परावर्तित प्रकाश पूर्णतः समतल ध्रुवित प्रकाश होता है। समतल धूवित प्रकाश के कम्पन कागज के तल के लम्बवत् होते हैं। अतः इन्हें बिन्दुओं द्वारा प्रदर्शित किया गया है। BD दिशा में अपवर्तित प्रकाश आंशिक रूप से ध्रुवित होता है।

व्याख्या अध्रुवित प्रकाश में विद्युत् वेक्टरों को दो आयताकार घटकों में वियोजित किया जा सकता है-
(1) आपतन तल के समान्तर और
(2) आपतन तल के लम्बवत्।

इन्हें चित्र में बिन्दुओं और तीरों के द्वारा प्रदर्शित किया गया है। जब प्रकाश-तरंग परावर्तक पृष्ठ पर पहुँचती है तो उसके इलेक्ट्रॉन इन दोनों दिशाओं में कम्पन करने लगते हैं। ध्रुवण कोण पर परावर्तित और अपवर्तित तरंगें परस्पर लम्बवत् होती हैं।

आपतन तल के समान्तर कम्पन परावर्तित तरंग के अनुदिश होते हैं । अत: ये कम्पन परावर्तित प्रकाश की दिशा में अनुप्रस्थ तरंगें उत्पन्न नहीं कर सकते। अतः परावर्तित तरंग में विद्युत् वेक्टर आपतन तल के लम्बवत् तल में कम्पन करते हैं। इस प्रकार परावर्तित प्रकाश पूर्णतः समतल ध्रुवित होता है। इसे चित्र में बिन्दुओं से प्रदर्शित किया गया है। अपवर्तित प्रकाश पूर्णतः ध्रुवित नहीं होता।

प्रश्न 9.
ब्रुस्टर का नियम क्या है ? सिद्ध कीजिए कि धुवण-कोण पर आपतित होने पर परावर्तित किरणें तथा अपवर्तित किरणें परस्पर लम्बवत् होती हैं ?
उत्तर:
ब्रुस्टर का नियम – लघु उत्तरीय प्रश्न क्रमांक 25 देखिए।
चित्र – परावर्तन द्वारा ध्रुवण-दीर्घ उत्तरीय प्रश्न क्रमांक 8 देखिए।
मानलो कोई प्रकाश किरण µ अपवर्तनांक वाले माध्यम के पृष्ठ पर ध्रुवण कोणत i_p पर आपतित होती है।
तब स्नेल के नियमानुसार,
µ = \(\frac{\sin i_{p}}{\sin r}\) ……….(1)
जहाँ r = अपवर्तन कोण
परन्तु µ = tan i_p ………..(2)
समी. (1) और (2) से,
tan i_p = \(\frac{\sin i_{p}}{\sin r}\)
या \(\frac{\sin i_{p}}{\cos i_{p}}=\frac{\sin i_{p}}{\sin r}\)
या cos i_p = sin r
या sin (90° – i_p) = sin r
या 90° – i_p = r
या i_p + r = 90°
उपर्युक्त प्रश्न के चित्र से स्पष्ट है कि
i_p + r + ∠CBD = 180°
या 90° + ∠CBD = 180°
∴ ∠CBD = 90°
अतः परावर्तित किरणें तथा अपवर्तित किरणें परस्पर लम्बवत् होती हैं।

प्रश्न 10.
प्रकाश के ध्रुवण से क्या तात्पर्य है ? प्रकीर्णन द्वारा ध्रुवण क्यों हो जाता है ? समझाइए।
उत्तर:

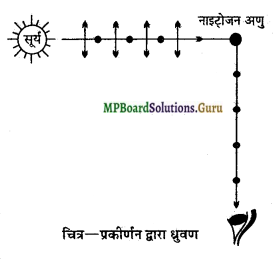
प्रकाश का ध्रुवण – प्रकाश का ध्रुवण उस घटना को कहते हैं, जिसमें प्रकाश के विद्युत्-वेक्टर प्रकाश संचरण की दिशा के लम्बवत् तल में एक ही दिशा में कम्पन करते हैं, प्रत्येक दिशा में सममित नहीं होते। दूसरे शब्दों में, प्रकाश तरंग द्वारा तरंग संचरण की दिशा के चारों ओर सममिति की कमी को प्रदर्शित करना प्रकाश का ध्रुवण कहलाता है।

प्रकीर्णन द्वारा ध्रुवण – यह पाया गया है कि सूर्य का प्रकाश वायुमण्डल के अणुओं द्वारा प्रकाणत हो जाता है। इस प्रकीर्णन के कारण सूर्य का प्रकाश ध्रुवित हो जाता है।

कीर्णन द्वारा ध्रुवण की व्याख्या निम्न प्रकार से की जा सकती है-
संलग्न चित्र में नाइट्रोजन अणु द्वारा आपतित प्रकाश का दो लम्बवत् दिशाओं में प्रकीर्णन द्वारा ध्रुवण प्रदर्शित किया गया है। आपतित प्रकाश अध्रुवित प्रकाश होता है, जिसमें विद्युत्-वेक्टर आपतित प्रकाश के लम्बवत् तल में हर सम्भव दिशा में कम्पन कर सकते हैं । इन समस्त कम्पनों को दो आयताका, घटकों में वियोजित किया जा सकता है-
(i) कागज के तल के समान्तर इन्हें तीरयुक्त रेखा से प्रदर्शित किया गया है।
(ii) कागज के तल के लम्बवत् इन्हें बिन्दुओं से प्रदर्शित किया गया है।
जब प्रकाश तरंग नाइट्रोजन के अणु पर आपतित होती है तो अणु के इलेव न इन दो लम्बवत् दिशाओं में कम्पन करने लगते हैं।

कागज के तल के समान्तर कम्पन प्रेक्षक के अनुदिश होते हैं । अत: ये कम्पन प्रेक्षक की दिशा में अनुप्रस्थ तरंग उत्पन्न नहीं कर सकते। इस प्रकार प्रेक्षक की आँख में प्रवेश करने वाला प्रकाश समतल ध्रुवित होता है, जिसके कम्पन कागज के तल के लम्बवत् होते हैं।

प्रश्न 11.
पोलेरॉइड क्या है ? इसकी बनावट, कार्य-विधि एवं उपयोग लिखिए।
उत्तर:
समतल ध्रुवित प्रकाश उत्पन्न करने वाली सरल व सस्ती युक्ति को पोलेरॉइड कहते हैं।
बनावट – इसमें एक फिल्म होती है जिसे काँच की दो प्लेटों के बीच रखा जाता है। इस फिल्म को बनाने के लिए नाइट्रो सेल्यूलोज की एक पतली शीट पर कार्बनिक यौगिक हरपेथाइट या आयडोक्वीनाइन सल्फेट के अति सूक्ष्म आकार के क्रिस्टल इस प्रकार फैलाकर रखे जाते हैं कि सभी क्रिस्टलों के अक्ष एक-दूसरे के समान्तर रहें।

जब साधारण प्रकाश पोलेरॉइड पर आपतित होता है तो उसके वे ही वैद्युत वेक्टर पोलेरॉइड में से निकल पाते हैं जिनके कम्पन क्रिस्टलों के अक्ष के समान्तर होते हैं। इस प्रकार पोलेरॉइड से निर्गत प्रकाश समतल-ध्रुवित प्रकाश होता है।


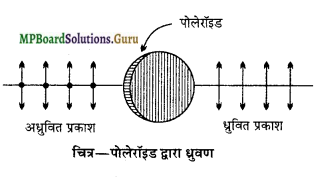
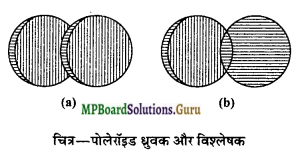
जब दोनों पोलेरॉइड एक-दूसरे के समान्तर होते हैं, तो पहले पोलेरॉइड (जिसे ध्रुवक कहते हैं) से निर्गत प्रकाश दूसरे पोलेरॉइड (जिसे विश्लेषक कहते हैं) से भी निर्गत हो जाता है, किन्तु जब वे एक-दूसरे के लम्बवत् होते हैं, तो पहले पोलेरॉइड
में निर्गत प्रकाश दूसरे पोलेरॉइड द्वारा अवरुद्ध हो जाता है। फलस्वरूप निर्गत प्रकाश की तीव्रता शून्य होती है। इस स्थिति में दोनों पोलेरॉइड क्रॉसित (Crossed) कहलाते हैं।

पोलेरॉइड के उपयोग –

1. प्रकाश की चकाचौंध दूर करने के लिए सनग्लासेस में।
2. मोटर कार के विंड स्क्रीन तथा हेडलाइट के कवर ग्लास पर पोलेरॉइड लगा दिये जाते हैं। पोलेरॉइडों के अक्ष ऊर्ध्वाधर से-45° के कोण पर झुके रहते हैं।
3. वायुयान और ट्रेन में प्रवेश करने वाले प्रकाश की तीव्रता को नियन्त्रित करने में।
4. तीन विमा वाले चित्रों को देखने में।
5. धातुओं के प्रकाशीय गुणों का अध्ययन करने में।

प्रश्न 12.
पोलेरॉइड क्या है ? समतल ध्रुवित प्रकाश पोलेरॉइड से कैसे प्राप्त करेंगे? आप समतल ध्रुवित प्रकाश और अधुवित प्रकाश में कैसे विभेद करेंगे?
उत्तर:
पोलेरॉइड – लघु उत्तरीय प्रश्न क्रमांक 31 देखिये।
सामान्य प्रकाश जो सीधे प्रकाश स्रोत से आपतित होती है उसे पहले पोलेरॉइड पर आपतित करते हैं। जो प्रकाश पोलेरॉइड से निर्गत होती है वह समतल ध्रुवित प्रकाश होती है। प्रकाश की ध्रुवित व अध्रुवित की पहचान के लिये पहले प्रकाश को पोलेरॉइड पर आपतित करते हैं।

यदि पोलेरॉइड को घुमाने से उससे निर्गत प्रकाश की तीव्रता में परिवर्तन होता है तो पोलेरॉइड पर आपतित प्रकाश ध्रुवित प्रकाश होगा और यदि निर्गत प्रकाश की तीव्रता में कोई परिवर्तन न हो तो पोलेरॉइड में आपतित प्रकाश अध्रुवित प्रकाश होगा।

प्रश्न 13.
प्रकाश के व्यतिकरण के द्वि-स्लिट प्रयोग में प्रकाश की अधिकतम तथा न्यूनतम तीव्रता के लिए शर्ते ज्ञात कीजिए।

अथवा

दो तरंगों के व्यतिकरण के लिए सैद्धान्तिक रूप से संपोषी एवं विनाशी व्यतिकरण के लिए प्रतिबन्ध ज्ञात कीजिए।

अथवा

प्रकाश के व्यतिकरण से आप क्या समझते हैं ? दो तरंगें जिनके आयाम a₁ व a₂ तथा कोणीय आवृत्ति ω है, अध्यारोपित होती हैं। संपोषी और विनाशी व्यतिकरण की स्थिति में तीव्रता ज्ञात कीजिए।
उत्तर:
व्यतिकरण – लघु उत्तरीय प्रश्न क्रमांक 2 देखिए।
मानलो एक ही आवृति की दो तरंगें एक ही दिशा में गमन कर रही हैं। उनके समी. निम्नलिखित हैं-
y₁ = a₁ sin ωt …..(1)
y₁ = a₁ sin (ωt + Φ) ……(2)
जहाँ a₁ और a₂ उनके आयाम तथा θ उनके मध्य कलान्तर है।
प्रत्येक तरंग की आवृत्ति υ = \(\frac{\omega}{2 \pi}\)
यदि दोनों तरंगें माध्यम के किसी बिन्दु पर एक साथ पहुंचे तो अध्यारोपण के सिद्धान्त से,
या y = y₁ + y₂
या y = a₁ sin ωt + a₂ sin(ωt + Φ)
या y = a₁ sin ωt + a₂ sin ωt cos Φ + a₂ cosωt sinΦ
या y = (a₁ + a₂ cos Φ)sin ωt + a₂ sinΦ cos ωt …….(3)
अब मानलो
a₁ + a₂ cos Φ = Rcos θ …….(4)
a₂ sinΦ = Rsin θ ………(5)
जहाँ R और θ नये नियतांक हैं।
समी. (3) में मान रखने पर,
y = R cos θ sin ωt + Rsin θ cos ωt
या y = R sin (ωt + θ) ……….(6)
समी. (6) परिणामी तरंग को प्रदर्शित करता है, जिसका स्वरूप अध्यारोपित तरंगों के समान ही है। अतः R परिणामी आयाम होगा।
समी. (4) और (5) को वर्ग करके जोड़ने पर,

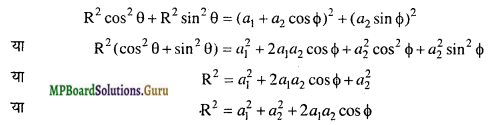
तीव्रता I आयाम R के वर्ग के अनुक्रमानुपाती होती है।
परिणामी तीव्रता I = K(a₁² + a₂² + 2a₁a₂ cos Φ)
जहाँ K एक आनुपातिक नियतांक है।
समी. (7) से स्पष्ट है कि परिणामी तीव्रता दोनों तरंगों के कलान्तर पर निर्भर करती है।

संपोषी व्यतिकरण के लिए शर्त – समी. (7) से स्पष्ट है कि अधिकतम तीव्रता के लिए,
cos Φ = 1
या Φ = 2nπ = 2πn, (जहाँ n = 0, 1, 2, 3, 4, ……..)
अत: जिन बिन्दुओं पर व्यतिकरण करने वाली तरंगें समान कला में मिलती हैं अर्थात् उनके मध्य कलान्तर 0 या π का सम गुणक होता है, उन बिन्दुओं पर परिणामी तीव्रता अधिकतम होती है।
इस प्रकार, I_max = K(a₁² + a₂² + 2a₁ – 1₂)
= K(a₁ + a₂)²
यदि संपोषी व्यतिकरण के लिए पथान्तर Δ हो, तो
Δ = \(\frac{\lambda}{2 \pi}\) × Φ
= \(\frac{\lambda}{2 \pi}\) × 2nπ

= 2n × \(\frac{\lambda}{2}\) = 0 या \(\frac{\lambda}{2}\) का सम गुणक।
विनाशी व्यतिकरण के लिए शर्त – समी. (7) से स्पष्ट है कि न्यूनतम तीव्रता के लिए,
cos Φ = -1
या Φ = (2n-1)π, (जहाँ n = 1, 2, 3, …….)
अतः जिन बिन्दुओं पर व्यतिकरण करने वाली तरंगें विपरीत कला में मिलती हैं या उनके मध्य कलान्तर T का विषम गुणक होता है, उन बिन्दुओं पर परिणामी तीव्रता न्यूनतम होती है।
इस प्रकार,
I_min = K(a₁² + a₂² + 2a₁ – a₂)
= K(a₁ – a₂)²
यदि विनाशी व्यतिकरण के लिए तरंगों के बीच पथान्तर Δ हो, तो
Δ = \(\frac{\lambda}{2 \pi}\) × Φ
= \(\frac{\lambda}{2 \pi}\)(2n – 1)π
= (2n – 1) \(\frac{\lambda}{2}=\frac{\lambda}{2}\)का विषम गुणक।
संपोषी व्यतिकरण की स्थिति में परिणामी तीव्रता के लिए व्यंजक-
समी. (7) में cos Φ = 1 रखने पर,
I = K(a₁² + a₂² + 2a₁a₂) = K(a₁ + a₂)²
यदि a₁ = a₂ = a हो, तो
I = K(a + a)² या I = 4Ka².
विनाशी व्यतिकरण की स्थिति में परिणामी तीव्रता के लिए व्यंजक-
समी. (7) में cos Φ = -1 रखने पर,
I = K(a₁² + a₂² – 2a₁a₂) = K(a₁ – a₂)²
यदि a₁ = a₂ = a हो, तो
I = K(a – a)² = 0.

प्रश्न 14.
यंग के द्विस्लिट प्रयोग में फ्रिंज चौड़ाई के लिए व्यंजक व्युत्पन्न कीजिये।
उत्तर:

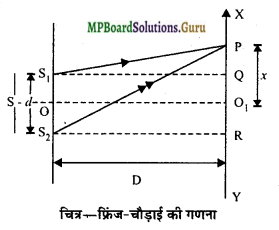
मानलो S एक स्लिट है जो एकवर्णी प्रकाश स्रोत से प्रकाशित है। S₁ और S₂ एक-दूसरे के समीप दो स्लिटें हैं जो S के समान्तर हैं तथा S से बराबर दूरी पर स्थित हैं। अत: S₁ और S₂ दो कला-सम्बद्ध स्रोत की तरह कार्य करेंगे।

मानलो S₁S₂ = d
मानलो दोनों स्रोतों S₁ और S₂ से D दूरी पर एक पर्दा XY है, जिस पर व्यतिकरण फ्रिजें बनती हैं।

पर्दे पर बिन्दु O₁, दोनों स्रोतों S₁ और S₂ से बराबर दूरी पर है। अतः इस बिन्दु पर दोनों स्रोतों से चलकर पहुंचने ts, वाली तरंगों के मध्य पथान्तर शून्य होगा। फलस्वरूप बिन्दु O₁ पर तीव्रता अधिकतम होगी ।
मानलो पर्दे पर बिन्दु0, सेx दूरी पर एक बिन्दु P है।
S₁ और S₂ से पर्दे XY पर S₁Q और S₂R लम्ब डालो।। मानलो S₁ और S₂ का मध्य बिन्दु O है। तब S,O और O₁ एक ही रेखा पर होंगे।
चित्र में,
PQ = O₁P- O₁Q = O₁P – OS₁ = x – \(\frac{d}{2}\)
तथा PR = O₁P+O₁R = O₁P+OS₂ = x + \(\frac{d}{2}\)
समकोण ΔPQS₁ में,
S₁P² = S₁Q² + PQ²
इसी तरह समकोण Δ PRS₂ में,

परन्तु S₂P = S₁P = D (लगभग) (क्योंकि व्यवहार में बिन्दु P बिन्दु D₁ के अत्यन्त निकट होता है।)
∴ S₂P – S₁P = \(\frac{2 x d}{2 \mathrm{D}}\)
अर्थात् पथान्तर S₂P-S₁P = \(\frac{x d}{\mathrm{D}}\) …….(1)

(i) दीप्त फ्रिन्जें (Bright Fringes) – अधिकतम तीव्रता के लिए व्यतिकरण करने वाली तरंगों के मध्य पथान्तर \(\frac{\lambda}{2}\) का समगुणक होता है।
∴ पथान्तर \(\frac{x d}{\mathrm{D}}=2 n \cdot \frac{\lambda}{2}\)
या \(\frac{x d}{\mathrm{D}}\) = nλ
∴ x = \(\frac{n \lambda \mathrm{D}}{d}\) …….(2)
जहाँ n = 0, 1, 2, 3, …
समीकरण (2) में n = 0 रखने पर केन्द्रीय दीप्त फ्रिन्ज की स्थिति प्राप्त होती है। इसे शून्य-क्रम फ्रिज कहते हैं।
n = 1, 2, 3, … रखने पर क्रमशः प्रथम, द्वितीय, तृतीय, ……दीप्त फ्रिन्जों की स्थितियाँ प्राप्त होती हैं।

(ii) अदीप्त फ्रिन्जे (Dark Fringes) – न्यूनतम तीव्रता के लिए व्यतिकरण करने वाली तरंगों के मध्य पथान्तर \(\frac{\lambda}{2}\) का विषम गुणक होता है।
∴ पथान्तर = \(\frac{x d}{\mathrm{D}}\)(2n – 1)\(\frac{\lambda}{2}\) (जहाँ n = 1, 2, 3 …)
या x = \(\frac{(2 n-1) \lambda . \mathrm{D}}{2 d}\) …..(3)
समी. (3) में n = 1, 2, 3, …… रखने पर क्रमश: प्रथम, द्वितीय, तृतीय, … अदीप्त फ्रिन्जों की स्थितियाँ प्राप्त होती हैं।
यदि केन्द्रीय फ्रिंज से n वीं एवं (n + 1) वीं दीप्त फ्रिजों की दूरियाँ क्रमश: x_n और x_n+1 हों, तो समी. (2) से,
x_n = \(\frac{n \lambda \mathrm{D}}{d}\)
तथा x_n+1 = \(\frac{(n+1) \lambda \mathrm{D}}{d}\)
अत: दो क्रमागत दीप्त फ्रेजों के बीच की दूरी अर्थात्-अदीप्त फ्रिंज की चौड़ाई,
x_n+1 – x_n = \(\frac{(n+1) \lambda D}{d}-\frac{n \lambda D}{d}=\frac{\lambda D}{d}\) …..(4)
इस तरह यदि केन्द्रीय फ्रिंज O से n वीं और (n+ 1) वीं अदीप्त फ्रिन्जों की दूरियाँ क्रमश: x_n औरx_n+1 हों, तो
x_n = \(\frac{(2 n-1) \mathrm{D} \lambda}{2 d}\)
तथा x_n+1 = \(\frac{(2 n+1) \mathrm{D} \lambda}{2 d}\)
अतः दो क्रमागत अदीप्त फ्रिन्जों के बीच की दूरी अर्थात् दीप्त फ्रिंज की चौड़ाई,
x_n+1 – x_n = \(\frac{(2 n+1) \mathrm{D} \lambda}{2 d}-\frac{(2 n-1) \mathrm{D} \lambda}{2 d}\)
\(=\frac{\mathrm{D} \lambda}{d}\) …..(5)
समी. (4) और (5) से स्पष्ट है कि दीप्त और अदीप्त फ्रिन्जों की चौड़ाई एकसमान होती है।
इस तरह फ्रिंज चौड़ाई = \(\frac{\mathrm{D} \lambda}{d}\) यही अभीष्ट व्यंजक है।

प्रश्न 15.
मेलस का नियम लिखिए तथा समझाइए।
उत्तर:
मेलस का नियम -“जब एक पूर्ण समतल ध्रुवित प्रकाश पुंज किसी विश्लेषक पर आपतित होता है तो निर्गत प्रकाश की तीव्रता ध्रुवक और विश्लेषक के पारित अक्षों (Pass axis) के बीच के कोण की कोज्या के वर्ग के अनुक्रमानुपाती होती है।”

यदि विश्लेषक पर आपतित प्रकाश की तीव्रता I₀ तथा उससे निर्गत प्रकाश की तीव्रता I तथा ध्रुवक एवं विश्लेषक के पारित अक्षों के बीच का कोण θ हो तो मेलस के नियम के अनुसार,
I ∝ cos² θ
I = I₀ cos² θ

व्युत्पत्ति – माना ध्रुवक का पारित अक्ष OP तथा विश्लेषक का पारित अक्ष OA है। माना OP तथा OA के बीच का कोण θ तथा ध्रुवक से निर्गत प्रकाश का OP के अनुदिश आयाम a है। आयाम a को दो घटकों में वियोजित किया जा सकता है-
(i) a cos θ विश्लेषक के पारित अक्ष के अनुदिश OA दिशा में
(ii) a sin θ विश्लेषक के पारित अक्ष के लम्बवत् OB दिशा में
इन दो घटकों में से केवल a cos θ घटक ही विश्लेषक से निर्गत होता है। अतः विश्लेषक से निर्गत प्रकाश की तीव्रता

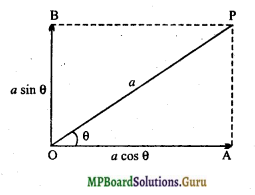
I ∝ (a cos θ)²
या I = Ka²cos²θ
जहाँ K एक आनुपातिक नियतांक है
या I = I₀ = cos² θ,I₀ = Ka²
अतः . I ∝ cos² θ.

आंकिक प्रश्न

प्रश्न 1.
वायुसे काँच में संक्रमण के लिए ब्रुस्टर कोण क्या है ? (काँच का अपवर्तनांक 1.5) (NCERT)
उत्तर:
दिया- μ = 1.5
सूत्र μ = tan i_p
∴ 1.5 = tan i_p
or
i_p = tan^-1(1.5) = 56.4°.

प्रश्न 2.
यंग के द्विस्लिट प्रयोग से फ्रिज चौड़ाई 4 मिमी हैं तो केन्द्रीय फ्रिन्ज से तृतीय अदीप्त फ्रिज की दूरी ज्ञात कीजिए।
उत्तर:
दिया है – β = 4 मिमी = 4 × 10^-3 मीटर
तृतीय अदीप्त फ्रिज के लिए n = 3
सूत्र – x_n = \(\left(\frac{2 n-1}{2}\right) \frac{\lambda D}{d}\)
mis \(\frac{\lambda D}{d}\) = β
∴ x_n = \(\left(\frac{2 n-1}{2}\right)\) β
x_n = \(\left(\frac{2 \times 3-1}{2}\right)\)4 × 10^-3 मीटर
या x_n = 10 × 10^-3 मीटर
या x_n = 10 मिमी।

प्रश्न 3.
एक पारदर्शक माध्यम का ध्रुवण कोण 60° है, तो निम्न को ज्ञात कीजिए-
(i) माध्यम का अपवर्तनांक।
(ii) अपवर्तन कोण।
उत्तर:
(i) दिया है i_p = 60°
तो ब्रुस्टर के नियम से, tan i_p = μ
या μ = tan 60°
या μ = 1.732.

(ii) ध्रुवण कोण पर आपतन के लिए,
i_p + r = 90°
जहाँ पर r = अपवर्तन कोण
मान रखने पर, 60 + r = 90°
r = 90° – 60°
r = 30°

प्रश्न 4.
यंग के प्रयोग में दोनों स्लिटों से पर्दे की दूरी 2 मीटर है। 6000Å तरंगदैर्घ्य का प्रकाश उन पर आपतित होता है
(i) यदि फ्रिंजों की चौड़ाई 2 मिमी हो, तो दोनों स्लिटों के बीच की दूरी ज्ञात कीजिए।
(ii) यदि आपतित प्रकाश का तरंगदैर्घ्य बदलकर 4800Å कर दिया जाता है, तो फ्रिजों की चौड़ाई ज्ञात कीजिए।
उत्तर:
दिया है- D = 2 मीटर, λ = 6000Å = 6000 × 10^-10 मीटर
(i) β = 2 मिमी = 2 × 10^-3 मीटर
सूत्र – β = \(\frac{\lambda \mathrm{D}}{d}\) से,
d = \(\frac{\lambda \mathrm{D}}{β}\) में मान रखने पर,
d = \(\frac{6000 \times 10^{-10} \times 2}{2 \times 10^{-3}}\)
या d = 6000 × 10^-7 = 6 × 10^-4
या d = 0.6 मिमी।

(ii) λ = 4800Å = 4800 × 10^-10 मीटर
उत्तर
सूत्र– β = \(\frac{\lambda \mathrm{D}}{d}\) में मान रखने पर,
β = \(\frac{4800 \times 10^{-10} \times 2}{6 \times 10^{-4}}\) =1600 × 10^-6
या β = 1.6 × 10^-4
या β = 1.6 मिमी।

वस्तुनिष्ठ प्रश्न
1. सही विकल्प चुनकर लिखिए

प्रश्न 1.
तरंगें एक स्थान से दूसरे स्थान तक संचरण करती हैं-
(a) द्रव्य
(b) आयाम
(c) ऊर्जा
(d) तरंगदैर्घ्य।
उत्तर:
(c) ऊर्जा

प्रश्न 2.
प्रकाश की तरंग प्रकृति का प्रमाण निम्न परिघटना से नहीं मिलता-
(a) व्यतिकरण
(b) विवर्तन
(c) ध्रुवण
(d) प्रकाश विद्युत प्रभाव।
उत्तर:
(d) प्रकाश विद्युत प्रभाव।

प्रश्न 3.
प्रकाश के व्यतिकरण में ऊर्जा-
(a) नष्ट हो जाती है
(b) पुनर्वितरित हो जाती है
(c) उत्पन्न हो जाती है
(d) इनमें से कोई नहीं।
उत्तर:
(b) पुनर्वितरित हो जाती है

प्रश्न 4.
निम्न में से कौन-सी परिघटना प्रकाश तरंगों में होती है किन्तु ध्वनि तरंगों में नहीं-
(a) अपवर्तन
(b) विवर्तन
(c) व्यतिकरण
(d) ध्रुवण।
उत्तर:
(a) अपवर्तन

प्रश्न 5.
प्रकाश के दो स्रोतों को कला-सम्बद्ध कहा जाता है जबकि उनके द्वारा उत्पादित तरंगों के-
(a) तरंगदैर्घ्य समान हों
(b) आयाम समान हों
(c) तरंगदैर्घ्य समान हों तथा कलान्तर नियत हों
(d) आयाम तथा तरंगदैर्घ्य समान हों।
उत्तर:
(c) तरंगदैर्घ्य समान हों तथा कलान्तर नियत हों

प्रश्न 6.
किसी बिन्दु पर दो तरंगें निम्न समीकरणों द्वारा निरूपित की जाती हैं-
E₁ = E₀ sinωt तथा E₂ = E₀ (sinωt + Φ). इस बिन्दु पर विनाशी व्यतिकरण उत्पन्न होगा यदि-
(a) Φ = 0
(b) Φ = π/2
(c) Φ = π
(d) Φ = 2π.
उत्तर:
(c) Φ = π

प्रश्न 7.
यंग के द्वि-स्लिट व्यतिकरण प्रयोग में यदि दोनों स्लिटों के बीच की दूरी एक-तिहाई कर दी जाती है तो फ्रिंज चौड़ाई होगी-
(a) \(\frac { 1 }{ 3 }\) गुनी
(b) 3 गुनी
(c) \(\frac { 1 }{ 9 }\) गुनी
(d) 9 गुनी।
उत्तर:
(b) 3 गुनी

प्रश्न 8.
यंग के प्रयोग में यदि दोनों स्लिटों के बीच की दूरी आधी तथा स्लिट और पर्दे के बीच की दूरी दुगुनी कर दी जाती है तो फ्रिज-चौड़ाई हो जायेगी-
(a) आधी
(b) एक-चौथाई
(c) दुगुनी
(d) चार गुनी।
उत्तर:
(d) चार गुनी।

प्रश्न 9.
यंग के द्विस्लिट प्रयोग में केन्द्रीय फ्रिंज की तीव्रता I है। एक स्लिट को बन्द कर देने पर इस स्थान पर तीव्रता I₀ हो जाती है। कौन-सा सम्बन्ध सत्य है-
(a) I = I₀
(b) I = 2I₀
(c) I = 4I₀
(d) I व I₀ में कोई सम्बन्ध नहीं है।
उत्तर:
(a) I = I₀

प्रश्न 10.
यदि y = usinωt और y₂ = 3sin\(\left(\omega t+\frac{\pi}{3}\right)\) द्वारा निरूपित दो तरंगें एक बिन्दु पर व्यतिकरण करती हैं। परिणामी तरंग का आयाम होगा लगभग
(a) 7
(b) 6
(c) 3
(d) 3.5
उत्तर:
(b) 6

प्रश्न 11.
यंग के द्वि-स्लिट प्रयोग में दीप्त और अदीप्त फ्रेिंजों की तीव्रताओं का अनुपात 4 : 1है। कला-सम्बद्ध स्रोतों के आयामों का अनुपात होगा-
(a) 4 : 1
(b) 3 : 1
(c) 2 : 1
(d) 1 : 1.
उत्तर:
(c) 2 : 1

प्रश्न 12.
प्रकाश का ध्रुवण सिद्ध करता है-
(a) प्रकाश का कणिका सिद्धान्त
(b) प्रकाश की अनुप्रस्थ तरंग प्रकृति
(c) प्रकाश की क्वाण्टम प्रकृति
(d) प्रकाश की अनुदैर्ध्य तरंग प्रकृति।
उत्तर:
(b) प्रकाश की अनुप्रस्थ तरंग प्रकृति

प्रश्न 13.
चश्मों में पोलेराइडों का उपयोग किया जाता है-
(a) फैशन के लिए
(b) चश्मे पर आपतित प्रकाश को काटने के लिए
(c) प्रकाश के ध्रुवण के लिए
(d) तरंग प्रकृति की जाँच करने के लिए।
उत्तर:
(c) प्रकाश के ध्रुवण के लिए

प्रश्न 14.
दो तरंगों के विस्थापन समीकरण y₁ = asinωt तथा y₂ = acos ωt हैं। दूसरी तरंग के सापेक्ष पहली तरंग की कला कितनी होगी-
(a) π से आगे
(b) π से पीछे
(c) π/2 से पीछे
(d) π/2 से आगे।
उत्तर:
(c) π/2 से पीछे

प्रश्न 15.
साबुन के रंगहीन घोल (बुलबुला) को श्वेत प्रकाश में देखने पर वह रंगीन दिखाई देता है। इसका । कारण है-
(a) परावर्तन
(b) अपवर्तन
(c) व्यतिकरण
(d) विवर्तन।
उत्तर:
(c) व्यतिकरण

2. रिक्त स्थानों की पूर्ति कीजिए

1. प्रकाश से संबंधित कणिका सिद्धान्त ………… ने दिया था।
उत्तर:
सर आइजक न्यूटन

2. व्यतिकरण में ………… का पुनर्वितरण होता है।
उत्तर:
ऊर्जा

3. संपोषी व्यतिकरण के लिए तरंगों के मध्य कलान्तर ………. होता है।
उत्तर:
2nπ

4. प्रकाश से संबंधित तरंग सिद्धान्त ……….. ने दिया था।
उत्तर:
हाइगन

5. प्रकाश के व्यतिकरण को प्रदर्शित करने वाला पहला प्रयोग ………. था।
उत्तर:
यंग का द्विस्लिट

6. यंग के द्विस्लिट प्रयोग में फ्रिन्ज चौड़ाई ……….. के व्युत्क्रमानुपाती होती है।।
उत्तर:
स्लिटों के मध्य दूरी

7. साबुन का बुलबुला रंगहीन प्रकाश में भी …………. की घटना के कारण रंगीन दिखाई देता है।
उत्तर:
व्यतिकरण

8. यदि 4 और 5 आयाम वाले प्रकाश के मध्य व्यतिकरण की घटना हो तो दीप्त और अदीप्त फ्रिन्जों की तीव्रता का अनुपात ……….. होता है।
उत्तर:
81 : 1

9. यदि ध्रुवण कोण i_p हो तो माध्यम का अपवर्तनांक ………… होता है।
उत्तर:
tan i_p

10. ध्रुवण कोण की स्थिति में किसी पारदर्शी माध्यम से अपवर्तित किरण और परावर्तित किरण के बीच कोण………………… होता है।
उत्तर:
90°

11. पोलेराइड से निर्गत प्रकाश ………… होता है।
उत्तर:
समतल ध्रुवित

12. एकल स्लिट द्वारा विवर्तन ………. विवर्तन का उदाहरण है।
उत्तर:
फ्रॉनहॉफर

13. ज्यामिति छाया में प्रकाश के अतिक्रमण की घटना को ………… कहते हैं।
उत्तर:
विवर्तन

14. कलासम्बद्ध स्रोतों के प्रकाश तरंगों के मध्य कलान्तर समय के साथ ………… रहता है।
उत्तर:
अपरिवर्तित

15. ………. दूरी से अधिक दूरी पर स्लिट से निर्गत प्रकाश का फैलाव स्लिट की चौड़ाई के बराबर होता है।
उत्तर:
फ्रेनेल

16. बादलों का स्पष्ट छायाचित्र खींचने के लिए कैमरे के लेंस के आगे ………………. लगा रहता है।
उत्तर:
पोलेरॉइड

17. प्रकाश स्रोत से असीमित दूरी पर निर्मित तरंगाग्र ………. तरंगाग्र होता है।
उत्तर:
समतल

3. उचित संबंध जोडिए
(A)

स्तम्भ ‘अ’	स्तम्भ ‘ब’
1. द्विस्लिट प्रयोग	(a) विवर्तन
2. ऋजुकोर द्वारा विवर्तन	(b) अनुप्रस्थ तरंग
3. ब्रुस्टर का नियम	(c) यंग
4. उच्चिष्ठ एवं निम्निष्ठ	(d) μ = tan i<sub>p</sub>
5. ध्रुवण	(e) फ्रेनेल विवर्तन।

उत्तर:
1. (c) यंग
2. (e) फ्रेनेल विवर्तन
3. (d) μ = tan i_p
4. (a) विवर्तन
5. (b) अनुप्रस्थ तरंग

(B)

स्तम्भ ‘अ’	स्तम्भ ‘ब’
1. यंग के प्रयोग में फ्रिज चौड़ाई	(a) \(\frac{\lambda}{2}\)
2 संपोषी व्यतिकरण के लिए पथान्तर	(b) \(\frac{2 \lambda D}{d}\)
3. विनाशी व्यतिकरण के लिए पथान्तर	(c) \(\frac{\lambda D}{d}\)
4. एकल स्लिट द्वारा विवर्तन में केन्द्रीय उच्चिष्ठ की चौड़ाई	(d) λ

उत्तर:
1. (c) \(\frac{\lambda D}{d}\)
2. (d) λ
3. (a) \(\frac{\lambda}{2}\)
4. (b) \(\frac{2 \lambda D}{d}\)

(C)

स्तम्भ ‘अ’	स्तम्भ ‘ब’
1. प्रकाश का कणिका सिद्धान्त	(a) हाइगेन
2. प्रकाश का तरंग सिद्धान्त	(b) व्यतिकरण
3. ज्यामितीय छाया में प्रकाश का अतिक्रमण	(c) न्यूटन
4. ऊर्जा का पुनर्वितरण	(d) विवर्तन
5. द्वितीयक तरंगिकाओं का सिद्धान्त	(e) मैक्सवेल।

उत्तर:
1. (c) न्यूटन
2. (e) मैक्सवेल
3. (d) विवर्तन
4. (b) व्यतिकरण
5. (a) हाइगेन

(D)

स्तम्भ ‘अ’	स्तम्भ ‘ब’
1. समतल तरंगाग्र	(a) Φ = 2nπ
2. फ्रिन्ज चौड़ाई (β)	(b) μ = tan i<sub>p</sub>
3. ब्रुस्टर का नियम	(c) पोलेरॉइड
4. समतल ध्रुवित प्रकाश उत्पन्न करने वाली युक्ति	(d) \(\frac{\lambda \mathrm{D}}{d}\)
5. सम्पोषी व्यतिकरण	(e) अनंत पर प्रकाश स्रोत।

उत्तर:
1. (e) अनंत पर प्रकाश स्रोत
2. (d) \(\frac{\lambda \mathrm{D}}{d}\)
3. (b) μ = tan i_p
4. (c) पोलेरॉइड
5. (a) Φ = 2nπ