In this article, we share MP Board Class 12th Maths Book Solutions Chapter 2 Inverse Trigonometric Functions Ex 2.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Solutions Chapter 2 Inverse Trigonometric Functions Ex 2.1
![]()
Find the principal values of the following.
Question 1.
sin-1\(\frac { -1 }{ 2 }\)
Solution:

Question 2.
cos-1\(\left(\frac{\sqrt{3}}{2}\right)\)
Solution:

Question 3.
cosec-1(2)
Solution:
The principal values branch of cosec-1 is

![]()
Question 4.
tan-1(-\(\sqrt{3}\))
Solution:
The principal values branch of tan-1 is
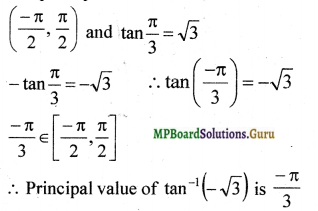
Question 5.
cos-1\(\frac { – 1 }{ 2 }\)
Solution:
The principal values branch of cos-1 is [0, π]

Question 6.
tan-1(-1)
Solution:
The principal values branch of tan-1 is

Question 7.
sec-1\(\left(\frac{2}{\sqrt{3}}\right)\)
Solution:
The principal values branch of sec-1 is

![]()
Question 8.
cot-1(\(\sqrt{3}\))
Solution:
The principal values branch of cot-1 is [0, π]
cot\(\frac { π }{ 6 }\) = \(\sqrt{3}\), \(\frac { π }{ 6 }\) ∈ [0, π]
∴ Priciapal value of cot-1\(\sqrt{3}\) is \(\frac { π }{ 6 }\)
Question 9.
cos-1\(\left(\frac{-1}{\sqrt{2}}\right)\)
Solution:
The principal values branch of cos-1 is [0, π]

Question 10.
cosec-1(\(\sqrt{-2}\))
Solution:
The principal values branch of cosec-1 is

![]()
Question 11.
tan-1(1) + cos-1(\(\frac { – 1 }{ 2 }\)) + sin-1(\(\frac { – 1 }{ 2 }\))
Solution:
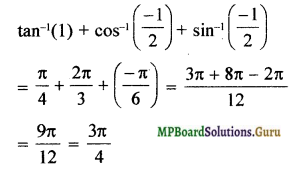
Question 12.
cos-1(\(\frac { 1 }{ 2 }\)) + 2 sin-1(\(\frac { 1 }{ 2 }\))
Solution:
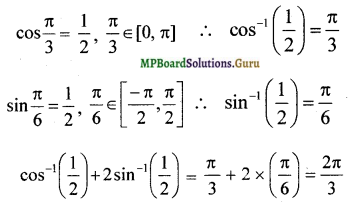
Question 13.
If sin-1 x = y, then
a. 0 ≤ y ≤ π
b. – \(\frac { π }{ 2 }\) ≤ y ≤ \(\frac { π }{ 2 }\)
c. 0 < y < π
d. – \(\frac { π }{ 2 }\) < y < \(\frac { π }{ 2 }\)
Solution:
b. – \(\frac { π }{ 2 }\) ≤ y ≤ \(\frac { π }{ 2 }\)
The principal values branch of sin-1 is
[\(\frac { – π }{ 2 }\), \(\frac { π }{ 2 }\)] . i.e., \(\frac { – π }{ 2 }\) ≤ y ≤ \(\frac { π }{ 2 }\)
![]()
Question 14.
tan-1\(\sqrt{3}\) – sec-1 ( – 2) is equal to
a. π
b . \(\frac { – π }{ 3 }\)
c. \(\frac { π }{ 3 }\)
d. \(\frac { 2π }{ 3 }\)
Solution:
b . \(\frac { – π }{ 3 }\)
tan-1\(\sqrt{3}\) – sec-1 ( – 2) = \(\frac { π }{ 3 }\) – \(\frac { 2π }{ 3 }\) = \(\frac { – π }{ 3 }\)