In this article, we share MP Board Class 12th Maths Book Solutions Chapter 1 Relations and Functions Ex 1.3 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Solutions Chapter 1 Relations and Functions Ex 1.3
![]()
Question 1.
Let f : {1,3,4} → (1,2, 5} and g: (1, 2, 5} → {1, 3} be given by f = {(1, 2), (3, 5), (4, 1)} and g = {(1, 3), (2, 3), (5, 1)}. Write down gof.
Solution:
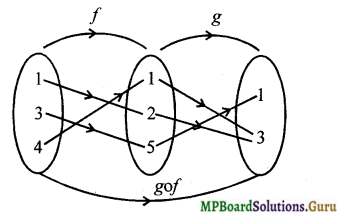
gof = {(1, 3),(3, 1), (4, 3)}
Question 2.
Let f, g and h be functions from R to R. Show that
i. (f + g)oh = foh + goh
ii. (f. g)oh = (foh) . (goh)
Solution:
i. (f + g)oh(x) = (f + g)h(x)) = f(h(x)) + g(h(x)) = (foh)(x) + (goh)(x)
∴ (f + g)oh = foh + goh
ii. (f. g)oh(x) = (f.g)(h(x))
= f(h(x)).g(h(x))
= (foh)(x). (goh)(x)
= [(foh).(goh)](x)
∴ (f. g)oh = (foh) . (goh)
Question 3.
Find gof and fog, if
i. f(x) = |x| and g(x) = |5x – 2|
ii. f(x) = 8x and g(x) = x\(x^{\frac{1}{3}}\)
(March 2014, SAY 2015, March 2016)
Solution:
i. (gof)(x) = g(f(x)) = g(|x|) = |5|x| – 2|
(fog)(x) = f(g(x)) = f(|5x – 2|)
= ||5x – 2|| = |5x – 2|
ii. (gof)(x) = g(f(x)) = g(8x³) = (8x³ )A1/3 = 2x
(fog)(x) = f(g(x)) = f(x1/3) = 8(x1/3)³ = 8x
![]()
Question 4.
If f(x) = \(\frac{(4 x+3)}{(6 x-4)}\), x ≠ 3, show that fof (x) = x, for all x ≠ \(\frac{2}{3}\). What is the inverse of f?
Solution:
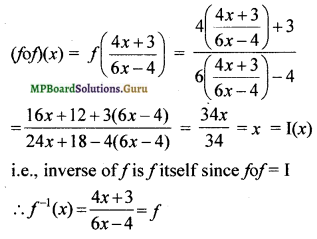
Another method:
Without using the result fof(x) = x, we can directly find the inverse off.

Question 5.
State with reason whether following functions have inverse
i. f : {1,2, 3,4} → {10} with
f = {(1, 10), (2, 10), (3, 10), (4, 10)}
ii. g: {5, 6, 7, 8} → {1, 2, 3, 4} with g ={(5, 4), (6, 3), (7, 4), (8, 2)}
iii. h : {2, 3,4, 5} → {7, 9, 11, 13} with h = {(2, 7), (3, 9), (4, 11), (5, 13)}
Solution:
i. The elements 1,2,3 and 4 have the same image.
∴ g is not one-one.
Hence g has no inverse.
ii. The image of the elements 5 and 7 is the same
∴ g is not one-one
Hence g has no inverse.
iii.
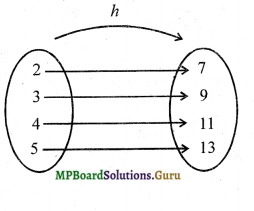
From the arrow diagram, it is clear that h is one-one and onto.
Hence h has inverse.
![]()
Question 6.
Show that f : [-1, 1] → R, given by f(x) = \(\frac{x}{(x+2)}\) is one-one. Find the inverse of the function f : [- 1, 1] → Range f.
Solution:
Let x1, x2 ∈ [-1, 1]
f(x1) = f(x2) ⇒ \(\frac{x_{1}}{2+x_{1}}\) = \(\frac{x_{2}}{2+x_{2}}\)
⇒ x1(2 + x2) = x2(2 + x1)
⇒ 2x1 + x1x2 = 2x2 + x1x2
⇒ 2x1 = 2x2
⇒ x1 = x2
∴ f is one-one
Let y = \(\frac{x}{x+2}\) ⇒ y(x + 2)= x
⇒ xy – x = – 2y
⇒ x (1 – y) = 2y
⇒ x = \(\frac{2y}{1-y}\), y ≠ 1
∴ f-1(x) = \(\frac{2x}{1-x}\)
Question 7.
Consider f : R → R given by f(x) = 4x + 3. Show that f is invertible. Find the inverse of f.
Solution:
f(x) = 4x + 3, x ∈ R
Domain of f = R and range of f = R
One-one
Let x1, x2 ∈ R
f(x1) = f(x2) ⇒ 4x1 + 3 = 4x2 + 3
⇒ 4x1 = 4x2
⇒ x1 = x2
∴ f is one-one.
Onto
Let y ∈ range of f such that y = f(x)

i.e., corresponding to every y ∈ R, there exists a real number \(\frac{y-3}{4}\) such that f(\(\frac{y-3}{4}\)) = y
∴ f is onto
Hence f is a bijection and f-1 exists
To find f-1
Let y = f(x)
Then x = \(\frac{y-3}{4}\) from (1)
∴ Inverse of/is given by f-1(x) = \(\frac{x-3}{4}\)
Question 8.
Consider f : R+ → [4, ∞) given by f(x) = x2 + 4. Show that f is invertible with the inverse f-1 of f given by f-1(y) = \(\sqrt{y-4}\), where R+ is the set of all non-negative real numbers.
Solution:
Let x1, x2 ∈ R+ such that f(x1) = f(x2)
⇒ x²1 + 4 = x²2 + 4
⇒ x²1 = x²2 ⇒ (x²1 – x²2) = 0
⇒ (x1 – x2) (x1 + x2) = 0
⇒ x1 – x2 = 0 since x1, x2 ∈ R
⇒ x1 = x2
∴ f is one-one.
Let y ∈ [4, ∞) such that y = f(x)
⇒ y = x2 + 4 ⇒ x2 = y – 4
⇒ x = \(\sqrt{y – 4}\) since x ∈ R+
i.e., x = \(\sqrt{y – 4}\) ∈ R++ …. (1)
f(x) = f(\(\sqrt{y – 4}\)) = (\(\sqrt{y – 4}\))² + 4
= y – 4 + 4 = y
∴ f is onto
Since f is one-one and onto, f is invertible.
To find f-1
Let y = x2 + 4
⇒ x = \(\sqrt{y – 4}\) from(1)
∴ f-1(y) = \(\sqrt{y – 4}\)
![]()
Question 9.
Consider f : R+ → [- 5, ∞) given by f(x) = 9x2 + 6x – 5. Show that f is invertible with f-1(y) = \(\left(\frac{(\sqrt{y+6})-1}{3}\right)\)
Solution:
Let y = 9x2 + 6x – 5 = (3x + 1)²
⇒ (3x + 1)² = y + 6
⇒ 3x + 1 = \(\sqrt{y + 6}\) ⇒ 3x = \(\sqrt{y + 6}\) – 1
⇒ x = \(\frac{\sqrt{y+6}-1}{3}\)
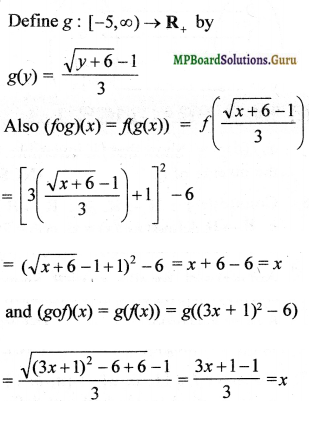
Hence gof = fog = Identity function. Hence f is invertible and
f-1(y) = \(\left(\frac{(\sqrt{y+6})-1}{3}\right)\)
Question 10.
Let f : X → Y be an invertible function. Show that f has unique inverse.
Solution:
Let g1 and g2 be two inverses of f.
Then for all y ∈ Y
(fog1)y = y and (fog2)y = y
⇒ (fog1)y = (fog2)(y)
⇒ f(g1(y)) = f(g2(y))
⇒ g1(y) = g2(y) since f is one-one
⇒ g1 = g2
Hence the inverse of f is unique.
![]()
Question 11.
Consider f : {1,2, 3} → {a, b,c} given by f(1) = a, f (2) = b and f(3) = c. Find f-1 and show that (f-1)-1 = f.
Solution:
f = {(1, a), (2, b), (3, c)}
f-1 = {(a, 1), (b, 2), (c, 3))
Clearly f is bijective
(f-1)-1 = {(1, a), (2, b), (3, c)} = f
Question 12.
Let f : X → Y be an invertible function. Show that the inverse of f-1 is f, i.e., (f-1)-1 = f.
Solution:
f : X → Y is invertible. Then f-1 : Y → X
Let x ∈ X , then y = f(x) ∈ Y such that f-1 (y) = x
Now (f-1of)(x) = f-1(f(x)) = f-1(y) = x
and (fof-1)(y) = f(f-1(y)) = f(x) = y
i.e., f-1 of and fof-1 are identity functions.
Hence they are inverse of each other.
i.e., the inverse of f-1 is f.
i.e., (f-1)-1 = f.
Question 13.
If f : R → R be given by f(x) = (3 – x3)\(\frac { 1 }{ 3 }\), then fof (x) is
a. x\(\frac { 1 }{ 3 }\)
b. x³
c. x
d. (3 – x³)
Solution:
c. x
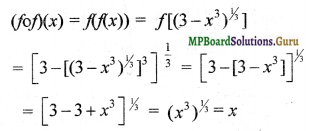
![]()
Question 14.
Let f : R – { – \(\frac { 4 }{ 3 }\) } → be a function defined as f(x) = \(\frac { 4x }{ 3x+4 }\). The inverse of f is the map g : Range f → R – \(\frac { 4 }{ 3 }\) given by
a. g(y) = \(\frac { 3y }{ 3-4y }\)
b. g(y) = \(\frac { 4y }{ 4-3y }\)
a. g(y) = \(\frac { 4y }{ 3-4y }\)
a. g(y) = \(\frac { 3y }{ 4-3y }\)
Solution:
b. g(y) = \(\frac { 4y }{ 4-3y }\)
Let \(\frac { 4x }{ 3x+4 }\) = y ⇒ 4x = 3xy + 4y
⇒ 4x – 3xy = 4y ⇒ x = \(\frac { 4y }{ 4-3y }\)
∴ g(y) = \(\frac { 4y }{ 4-3y }\).