In this article, we share MP Board Class 12th Maths Book Solutions Chapter 10 सदिश बीजगणित Ex 10.3 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Book Solutions Chapter 10 सदिश बीजगणित Ex 10.3
प्रश्न 1.
दो सदिशों \(\vec{a}\) तथा \(\vec{b}\) के परिमाण क्रमशः \(\sqrt{3}\) व 2 हैं। और \(\vec{a} \cdot \vec{b}=\sqrt{6}\) हैं, तो \(\vec{a}\) और \(\vec{b}\) के बीच का कोण ज्ञात कीजिए।
हल:
दो सदिश \(\vec{a}\) और \(\vec{b}\) है के बीच का कोण हो तो

प्रश्न 2.
सदिशों \(\hat{i}-2 \hat{j}+3 \hat{k}\) और \(3 \hat{i}-2 \hat{j}+\hat{k}\) के बीच का कोण ज्ञात कीजिए
हल:
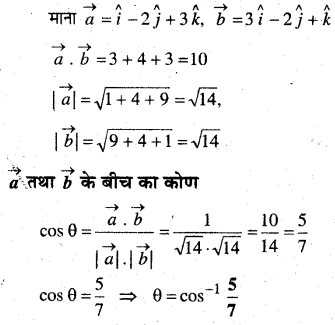
प्रश्न 3.
सदिश \(\hat{\boldsymbol{i}}+\hat{\boldsymbol{j}}\) पर सदिश \(\hat{\boldsymbol{i}}-\hat{\boldsymbol{j}}\) का प्रक्षेप ज्ञात कीजिए।
हल:

प्रश्न 4.
सदिश \(\hat{i}+3 \hat{j}+7 \hat{k}\) का, सदिश \(7 \hat{i}-\hat{j}+8 \hat{k}\) पर प्रक्षेप ज्ञात कीजिए।
हल:
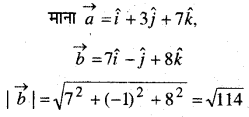
![]()
प्रश्न 5.
दर्शाइए कि दिए हुए निम्नलिखित तीन सदिशों में से प्रत्येक मात्रक सदिश हैं- \(\frac{1}{7}(2 \hat{i}+3 \hat{j}+6 \hat{k})\),\(\frac{1}{7}(3 \hat{i}-6 \hat{j}+2 \hat{k}) \frac{1}{7}(6 \hat{i}+2 \hat{j}-3 \hat{k})\) यह भी दर्शाइए कि सदिश परस्पर एक-दूसरे के लम्बवत् हैं।
हल:
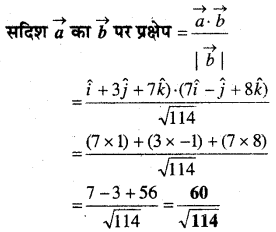

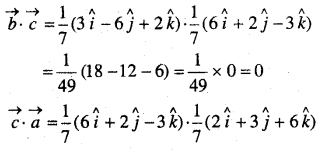
अतः सदिश परस्पर एक-दूसरे के लम्बवत् हैं।
प्रश्न 6.
यदि \((\vec{a}+\vec{b}) \cdot(\vec{a}-\vec{b})\) = 8 और \(|\vec{a}|=8|\vec{b}|\) हो तो \(|\vec{a}|,|\vec{b}|\) ज्ञात कीजिए।
हल:
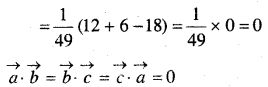
प्रश्न 7.
\((3 \vec{a}-5 \vec{b}) \cdot(2 \vec{a}+7 \vec{b})\) का मान ज्ञात कीजिए।
हल:

प्रश्न 8.
दो सदिशों \(\vec{a}\) और \(\vec{b}\) के परिमाण ज्ञात कीजिए यदिइनके परिमाण समान हैं और इनके बीच का कोण 60° है, तथा इनका अदिश गुणनफल \(\frac{1}{2}\) है।
हल:
हम जानते हैं कि सदिश \(\vec{a}\) तथा \(\vec{b}\) के बीच का कोण
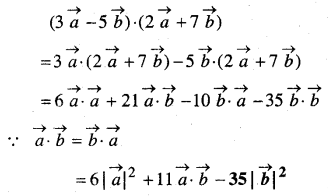
![]()
प्रश्न 9.
यदि एक मात्रक सदिश \(\vec{a}\) के लिए \((\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})\) = 12 हो तो| \(|\vec{x}|\) ज्ञात कीजिए।
हल:

प्रश्न 10.
यदि \(\vec{a}=2 \hat{i}+2 \hat{j}+3 \hat{k}\), \(\vec{b}=-\hat{i}+2 \hat{j}+\hat{k}\) और \(\vec{c}=3 \hat{i}+\hat{j}\) इस प्रकार है कि \(\vec{a}+\lambda \vec{b}, \vec{c}\), पर लम्ब है तो λ का मान ज्ञात कीजिए।
हल:
दिया है \(\vec{a}+\lambda \vec{b}, \vec{c}\) पर लम्ब हैं।

प्रश्न 11.
दर्शाइए कि दो शून्येत्तर सदिशों \(\vec{a}\) और \(\vec{b}\) के लिए \(|\vec{a}| \cdot \vec{b}+|\vec{b}| \vec{a},|\vec{a}| \cdot \vec{b}-|\vec{b}| \vec{a}\) पर लम्ब है।
हल:

प्रश्न 12.
यदि \(\vec{a} \cdot \vec{a}\) = 0 और \(\vec{a} \cdot \vec{b}\) = 0 तो सदिश \(\vec{a}\) के बारे में क्या निष्कर्ष निकाला जा सकता है?
हल:
दिया है \(\vec{a} \cdot \vec{a}\) = 0 तथा \(\vec{a} \cdot \vec{b}\) = 0
अत: \(\vec{a}\) = 0
तब \(\vec{b}\) भी सदिश हो सकता है।
![]()
प्रश्न 13.
यदि \(\vec{a}, \vec{b}, \vec{c}\) हे मात्रक सदिश इस प्रकार हैं, कि \(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\) तो \(\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}\) का मान ज्ञात कीजिए।
हल:

प्रश्न 14.
यदि \(\vec{a}=\overrightarrow{0}\) अथवा \(\vec{b}=\overrightarrow{0}\) तब \(\vec{a} \cdot \vec{b}=0\) परन्तु विलोम का सत्य होना आवश्यक नहीं है। एक उदाहरण द्वारा अपने उत्तर की पुष्टि कीजिए।
हल:

प्रश्न 15.
यदि किसी ∆ABC के शीर्ष A, B, C क्रमशः (1, 2, 3), (-1, 0, 0) (0, 1, 2) हैं, तो ∠ABC ज्ञात कीजिए। [∠ABC सदिशों \(\overrightarrow{B A}\) एवं \(\overrightarrow{B C}\) के बीच का कोण है।]
हल:
∠ ABC सदिशों \(\overrightarrow{B A}\) तथा \(\overrightarrow{B C}\) के बीच का कोण है

प्रश्न 16.
दर्शाइए कि बिन्दु A (1, 2, 7), B(2, 6, 3) और C(3, 10, -1) संरेख हैं।
हल:
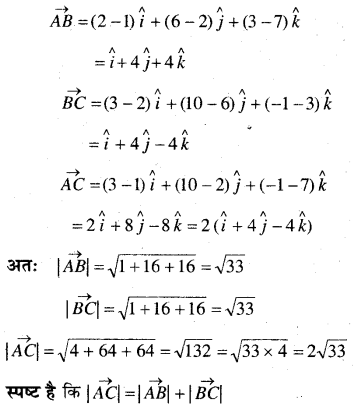
अतः तीनों बिन्दु संरेख हैं।
![]()
प्रश्न 17.
दर्शाइए कि सदिश \(2 \hat{i}-\hat{j}+\hat{k}, \hat{i}-3 \hat{j}-5 \hat{k}\) और \(3 \hat{i}-4 \hat{j}-4 \hat{k}\) एक समकोण त्रिभुज के शीर्षों की रचना करते हैं।
हल:
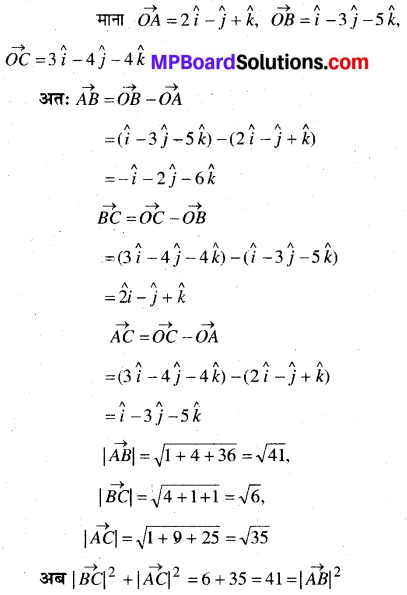
अतः दिए गए सदिश समकोण त्रिभुज के शीर्ष हैं।
प्रश्न 18.
यदि शून्येतर सदिश \(\vec{a}\) का परिमाण a है और λ एक शून्येतर अदिश है तो λ\(\vec{a}\) एक मात्रक सदिश है यदि-
(A) λ = 1
(B) λ = -1
(C) a =| λ|
(D) a = \(\frac{1}{|\lambda|}\)
हल:
