MP Board Class 12th Maths Important Questions Chapter 9 अवकल समीकरण
अवकल समीकरण Important Questions
अवकल समीकरण वस्तुनिष्ठ प्रश्न
प्रश्न 1.
सही विकल्प चुनकर लिखिए –
प्रश्न 1.
अवकल समीकरण \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) + x2 \(\frac{dy}{dx}\) = ex की घात है –
(a) 1
(b) 2
(c) 3
(d) अस्तित्व नहीं है।
उत्तर:
(c) 3
प्रश्न 2.
अवकल समीकरण (1 + x) y dx + (1 – y) x dy = 0 का हल होगा –
(a) log xy + x + y = c
(b) log y + x – y = c
(c) log xy – x – y = c
(d) log xy – x + y = c.
उत्तर:
(b) log y + x – y = c
![]()
प्रश्न 3.
उन सभी वृत्तों का अवकल समीकरण जो मूलबिन्दू से गुजरते हैं तथा जिनके केन्द्र X – अक्ष पर स्थित है –
(a) x2 = y2 + xy \(\frac{dy}{dx}\)
(b) x2 = y2 + 3xy \(\frac{dy}{dx}\)
(c) y2 = x2 + 2xy \(\frac{dy}{dx}\)
(d) y2 = x2 – 2xy \(\frac{dy}{dx}\)
उत्तर:
(c) y2 = x2 + 2xy \(\frac{dy}{dx}\)
प्रश्न 4.
अवकल समीकरण \(\frac{dy}{dx}\) + y = e-x, y(0) = 0 का हल होगा –
(a) y = e-x (x -1)
(b) y = xex
(c) y = xe-x + 1
(d) y = xe-x
उत्तर:
(d) y = xe-x
प्रश्न 5.
सरल रेखा जो अवकल समीकरण \(\frac{dy}{dx}\) = m को संतुष्ट करती हो तथा Y – अक्ष पर धनात्मक दिशा में 3 अन्तःखण्ड काटती हो, है –
(a) y = mx + c
(b) = mx + 3
(c) y = mx – 3
(d) y = – mx + 3
उत्तर:
(b) = mx + 3
![]()
प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिये –
- समीकरण x2 + y2 = a2 के संगत अवकल समीकरण ……………………….. है।
- वक्र y = ecx से संबंधित अवकल समीकरण …………………………….. है, जहाँ c स्वेच्छ अचर है।
- रेखीय अवकल समीकरण \(\frac{dy}{dx}\) + Py = Q में समाकलन गुणांक …………………………. है।
- रेखीय अवकल समीकरण \(\frac{dy}{dx}\) + Py = Q में P और …………………………… हैं।
- अवकल समीकरण (x + y + 1) dy = dx ………………………… रूप का है।
- अवकल समीकरण e-x+y \(\frac{dy}{dx}\) = 1 का हल हो ……………………… है।
उत्तर:
- y \(\frac{dy}{dx}\) + x = 0
- x\(\frac{dy}{dx}\) = y log y
- e∫pdx
- अचर
- रेखीय अवकल समीकरण
![]()
प्रश्न 3.
निम्न कथनों में सत्य/असत्य बताइए –
- अवकल समीकरण y = x ( \(\frac{dy}{dx}\) )2 + \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) की कोटि 2 है।
- अवकल समीकरण ( \(\frac { d^{ 3 }y }{ dx^{ 3 } } \) )4/5 – 2 ( \(\frac{dy}{dx}\) ) ( \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) )2 = 0 की घात 5 है।
- अवकल समीकरण x \(\frac{dy}{dx}\) – y = 2x2 का समाकलन गुणांक e-x है।
- अवकल समीकरण dy = sin x dx का हल y + cos x – c = 0 है।
- अवकल समीकरण ydx + (x – y3) dy = 0 का हल xy = \(\frac { y^{ 4 } }{ 4 } \) + c है।
उत्तर:
- सत्य
- असत्य
- असत्य
- सत्य
- सत्य।
![]()
प्रश्न 4.
एक शब्द/वाक्य में उत्तर दीजिए –
- अवकल समीकरण (1 + y2) + (2xy – cot y) \(\frac{dy}{dx}\) = 0 का समाकल गुणांक लिखिए।
- अवकल समीकरण (1 + x2)dy = (1 + y2) dx का हल ज्ञात कीजिए।
- अवकल समीकरण y = x( \(\frac{dy}{dx}\) )2 + \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) की कोटि व घात का योग लिखिए।
- अवकल समीकरण dy = sin x dx का हल y + cos x – c = 0 है।
- अवकल समीकरण \(\frac{dy}{dx}\) + \(\frac{1}{x}\) = \(\frac { e^{ y } }{ x^{ 2 } } \) का हल ज्ञात कीजिए।
उत्तर:
- 1 + y2
- x – y = c (1 + xy)
- 3
- log x
- 2xe-y = cx2 + 1.
अवकल समीकरण अति लघु उत्तरीय प्रश्न
प्रश्न 1.
अवकल समीकरण \(\frac{dy}{dx}\) + y = e-x की कोटि तथा घात ज्ञात कीजिये।
उत्तर:
1, 1
प्रश्न 2.
अवकल समीकरण ( \(\frac{dy}{dx}\) )3 = \(\sqrt { 1+(\frac { dy }{ dx } )^{ 2 } } \) की कोटि तथा घात ज्ञात कीजिये।
उत्तर:
1, 6
प्रश्न 3.
अवकल समीकरण \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) + \(\sqrt { 1+(\frac { dy }{ dx } )^{ 3 } } \) = 0 की कोटि तथा घात ज्ञात कीजिये।
उत्तर:
2, 2
![]()
प्रश्न 4.
वृत्त के समीकरण x2 + y2 = a2 के संगत अवकल समीकरण क्या होगा?
उत्तर:
y \(\frac{dy}{dx}\) + x = 0
प्रश्न 5.
सरल रेखा y = mx + c के लिये अवकल समीकरण बनाइये।
उत्तर:
\(\frac{dy}{dx}\) = m
प्रश्न 6.
अवकल समीकरण \(\frac{dy}{dx}\) = 4y को हल कीजिये।
उत्तर:
y = c.e4x
प्रश्न 7.
x2 \(\frac{dy}{dx}\) = 2 का व्यापक हल ज्ञात कीजिये।
उत्तर:
y = c – \(\frac{2}{x}\)
![]()
प्रश्न 8.
अवकल समीकरण dy = sin x dx का हल ज्ञात कीजिये।
उत्तर:
y + cos x = c
प्रश्न 9.
\(\frac{dy}{dx}\) + Px = Q रूप वाले अवकल समीकरण का व्यापक हल ज्ञात कीजिये।
उत्तर:
xe∫pdy = ∫Q.e∫pdy.dy + c
प्रश्न 10.
अवकल समीकरण (1 – y2) \(\frac{dy}{dx}\) + yx = ay का समाकल गुणांक ज्ञात कीजिये।
उत्तर:
\(\frac { 1 }{ \sqrt { 1-y^{ 2 } } } \)
अवकल समीकरण लघु उत्तरीय प्रश्न
प्रश्न 1.
अवकल समीकरण x log x dy – y dx = 0?
हल:
दिया है:
⇒ xlog x dy = y dx
⇒ \(\frac{1}{y}\) \(\frac{dy}{dx}\) = \(\frac{1}{xlogx}\) dx
⇒ ∫\(\frac{1}{y}\) \( dy = ∫[latex]\frac{1}{xlogx}\) dx
⇒ log y = ∫\(\frac{1}{t}\) dt (माना log x = t, \(\frac{1}{x}\) \( dx = dt)
⇒ log y = log t + log c
⇒ log y = log log x + log c
प्रश्न 2.
अवकल समीकरण dy/dx = ex-y + x.e-y को हल कीजिए।
हल:
दिया है:
[latex]\frac{dy}{dx}\) = ex-y + x.e-y
⇒ \(\frac{dy}{dx}\) = e-y(ex + x)
⇒ ey dy = (ex + x) dx
दोनों पक्षों का समाकलन करने पर,
∫ey dy = ∫(ex + x) dx
ey = ex + \(\frac { x^{ 2 } }{ 2 } \) + c
![]()
प्रश्न 3.
सिद्ध कीजिए कि y = 4 sin 3x अवकल समीकरण \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) + 9y = 0 का एक हल है।
हल:
दिया है:
y = 4 sin 3x ……………… (1)
x के सापेक्ष अवकलन करने पर,
∴ \(\frac{dy}{dx}\) = 12 cos 3x
पुनः x के सापेक्ष अवकलन करने पर,
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = -36 sin 3x = -9 × 4 sin 3x
⇒ \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = -9y, [समी. (1) से]
⇒ \(\frac { d^{ 2 }y }{ dx^{ 2 } } \)+ 9y = 0 यही सिद्ध करना था।
प्रश्न 4.
अवकल समीकरण \(\frac{dy}{dx}\) = sec x (sec x + tan x) का हल ज्ञात कीजिए।
हल:
दिया गया अवकल समीकरण है:
\(\frac{dy}{dx}\) = sec x (sec x + tan x)
⇒ dy = (sec2x + sec x tan x) dx
⇒ ∫dy = ∫sec2x dx + ∫sec x tan x dx
∴ y = tan x + sec x + c
![]()
प्रश्न 5.
अवकल समीकरण \(\frac{dy}{dx}\) = sec2 x + 3x2 को हल कीजिए।
हल:
\(\frac{dy}{dx}\) = sec2 x + 3x2
⇒ dy = (sec2 x + 3x2) dx
⇒ ∫dy = ∫sec2 x dx + 3∫x2 dx
⇒ y = tan x + \(\frac { 3x^{ 3 } }{ 3 } \) + c
⇒ y = tan x + x3 + c
प्रश्न 6.
अवकल समीकरण \(\frac{dy}{dx}\) = sec2 x + 2x का हल ज्ञात कीजिए।
हल:
प्रश्न क्र. 5 की भाँति हल करें।
प्रश्न 7.
अवकल समीकरण \(\frac{dy}{dx}\) = (3x2 + 2) को हल कीजिए।
हल:
दिया है:
\(\frac{dy}{dx}\) = (3x2 + 2)
⇒ dy = (3x2 + 2) dx
⇒ ∫dy = ∫(3x2 + 2) dx
⇒ y = 3 × \(\frac { x^{ 3 } }{ 3 } \) + 2x + c = x3 + 2x + c
![]()
प्रश्न 8.
अवकल समीकरण x2 \(\frac{dy}{dx}\) = 2 को हल कीजिए।
उत्तर:
x2 \(\frac{dy}{dx}\) = 2
⇒ dy = 2.x-2 dx
⇒ ∫dy = 2∫x-2 dx
⇒ y = 2( \(\frac{-1}{x}\) ) + c
प्रश्न 9.
अवकल समीकर \(\frac{dy}{dx}\) = x3 + sin 4x का हल ज्ञात कीजिये।
दिया है:
\(\frac{dy}{dx}\) = x3 + sin 4x
⇒ dy = (x3 + sin 4x) dx
⇒ ∫dy = ∫x3 dx + ∫sin 4x dx
⇒ y = \(\frac { x^{ 4 } }{ 4 } \) + ( \(\frac { -cos4x }{ 4 } \) ) + c
⇒ y = \(\frac { x^{ 4 } }{ 4 } \) – \(\frac{cos4x}{4}\) + c
प्रश्न 10.
अवकल समीकरण \(\frac{dy}{dx}\) + 2x = e3x का हल ज्ञात कीजिये।
हल:
दिया है:
\(\frac{dy}{dx}\) + 2x = e3x
⇒ \(\frac{dy}{dx}\) = e3x – 2x
⇒ dy = (e3x – 2x) dx
⇒ ∫dy = ∫e3x dx – 2∫x dx
⇒ y = e3x. \(\frac{1}{3}\) – \(\frac { 2x^{ 2 } }{ 2 } \) + c = \(\frac{1}{3}\) e3x – x2 + c
प्रश्न 11.
अवकल समीकरण \(\frac{dy}{dx}\) = \(\frac { cos^{ 2 }y }{ sin^{ 2 }x } \) का हल ज्ञात कीजिये।
हल:
\(\frac{dy}{dx}\) = \(\frac { cos^{ 2 }y }{ sin^{ 2 }x } \)
⇒ \(\frac { 1 }{ cos^{ 2 }y } \) dy = \(\frac { 1 }{ sin^{ 2 }x } \) dx
⇒ sec2 ydy = cosec2 xdx
⇒ ∫sec2 ydy = ∫cosec2 xdx
⇒ tan y = – cot x + c
प्रश्न 12.
अवकल समीकरण (x2 + 1) \(\frac{dy}{dx}\) = 1 को हल कीजिये।
हल:
दिया है:
(x2 + 1) \(\frac{dy}{dx}\) = 1
⇒ \(\frac{dy}{dx}\) = \(\frac { 1 }{ (1+x^{ 2 }) } \)
⇒ dy = \(\frac { 1 }{ (1+x^{ 2 }) } \) dx
⇒ ∫dy = ∫\(\frac { 1 }{ (1+x^{ 2 }) } \) dx
⇒ y = tan-1 x + c
![]()
प्रश्न 13.
समीकरण \(\frac{dy}{dx}\) = sin x sin y को हल कीजिये।
हल:
\(\frac{dy}{dx}\) = sin x sin y
⇒ cosec y dy = sin x dx
समाकलन करने पर,
-loge(cosec y + cot y) = – cos x + c
⇒ cos x – loge(cosec y + cot y) = c
प्रश्न 14.
अवकल समीकरण \(\frac{dy}{dx}\) = y sin x को हल कीजिये।
हल:
\(\frac{dy}{dx}\) = y sin x
⇒ \(\frac{1}{y}\) \(\frac{dy}{dx}\) = sin x
⇒ ∫\(\frac{1}{y}\) dy = ∫sin x dx
⇒ log y = – cos x + c
प्रश्न 15.
अवकल समीकरण \(\frac{dy}{dx}\) = x cos x को हल कीजिये।
हल:
दिया है:
\(\frac{dy}{dx}\) = x cos x
⇒ dy = x cos x dx
⇒ ∫dy = ∫x cos x dx
⇒ y = x sin x – ∫1. sin x dx + c
⇒ y = x sin x + cos x + c
प्रश्न 16.
अवकल समीकरण \(\frac{dy}{dx}\) = 1 – x + y – xy को हल कीजिए।
हल:
दिया गया अवकल समीकरण है –
\(\frac{dy}{dx}\) = 1 – x + y – xy
⇒ \(\frac{dy}{dx}\) = (1 – x) + y(1 – x)
⇒ \(\frac{dy}{dx}\) = (1 – x) (1 + y)
⇒ \(\frac{dy}{1+y}\) = (1 – x)dx
⇒ ∫\(\frac{dy}{1+y}\) = ∫(1 – x)dx
⇒ loge(1 + y) = x – \(\frac { x^{ 2 } }{ 2 } \) + c
![]()
प्रश्न 17.
अवकल समीकरण \(\frac{dy}{dx}\) = (1 + x)(1 + y2) को हल कीजिए।
हल:
दिया गया अवकल समीकरण है:
\(\frac{dy}{dx}\) = (1 + x)(1 + y2)
⇒ \(\frac { 1 }{ 1+y^{ 2 } } \) dy = (1 + x) dx
समाकलन करने पर,
⇒ tan-1 y = x + \(\frac { x^{ 2 } }{ 2 } \) + c
प्रश्न 18.
अवकल समीकरण हल कीजिए –
\(\frac{dy}{dx}\) = cot2x
⇒ dy = cot2 x dx
⇒ ∫dy = ∫cot2 x dx
⇒ y = ∫(cosec2 x – 1) dx
⇒ y = – cot x – x + c
अवकल समीकरण दीर्घ उत्तरीय प्रश्न-I
प्रश्न 1.
(A) अवकल समीकरण \(\frac{dy}{dx}\) + y tan x = sec x को हल कीजिए।
हल:
दिया है:
\(\frac{dy}{dx}\) + y tan x = sec x ………… (1)
यह एक रैखिक अवकल समीकरण है, इसकी तुलना \(\frac{dy}{dx}\) + Py = Q से करने पर,
P = tan x, Q = sec x
∴ I.F. = e∫p dx = e∫tan x dx = elog secx
⇒ I.F. = sec x
अतः अवकल समी. (1) का अभीष्ट हल है:
y × (I.F.) = ∫Q × (I.F). dx + c
⇒ y × (sec x) = ∫sec x × (sec x) dx + c
= ∫sec2 xdx + c
⇒ y sec x = tan x + c
(B) अवकल समीकरण \(\frac{dy}{dx}\) + y tan x = sin x को हल कीजिए।
हल:
प्रश्न क्रमांक 1 (A) की भाँति हल करें।
![]()
प्रश्न 2.
अवकल समीकरण \(\frac { dy }{ dx } \) = \(\frac { \sqrt { 1-y^{ 2 } } }{ \sqrt { 1-x^{ 2 } } } \) को हल कीजिए।
हल:
\(\frac{dy}{dx}\) = \(\frac { \sqrt { 1-y^{ 2 } } }{ \sqrt { 1-x^{ 2 } } } \)

![]()
प्रश्न 3.
अवकल समीकरण 3x2dy = (3xy + y2)dx को हल कीजिए।
हल:
दिया गया अवकल समीकरण है:
3x2 dy = (3xy + y2) dx
⇒ \(\frac{dy}{dx}\) = \(\frac { 3xy+y^{ 2 } }{ 3x^{ 2 } } \) ……….. (1)
माना y = vx
⇒ \(\frac{dy}{dx}\) = v + x \(\frac{dv}{dx}\)
समी. (1) में मान रखने पर,

प्रश्न 4.
अवकल समीकरण हल कीजिए –
(1 + x)2 \(\frac{dy}{dx}\) + 2xy = 4x2
हल:
दिया गया अवकल समीकरण है:
(1 + x2) \(\frac{dy}{dx}\) + 2xy = 4x2
⇒ \(\frac{dy}{dx}\) + \(\frac { 2xy }{ 1+x^{ 2 } } \) = \(\frac { 4x^{ 2 } }{ 1+x^{ 2 } } \)
इसकी तुलना रैखिक अवकल समीकरण \(\frac{dy}{dx}\) + Py = Q से करने पर,
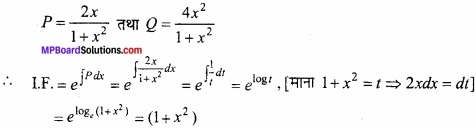
अतः अभीष्ट हल होगा:

प्रश्न 5.
अवकल समीकरण (1 + x2) \(\frac{dy}{dx}\) + 2xy = cos x को हल कीजिए।
हल:
दिया है:
(1 + x2) \(\frac{dy}{dx}\) + 2xy = cos x
⇒ \(\frac{dy}{dx}\) + \(\frac { 2x }{ (1+x^{ 2 }) } \). y = \(\frac { cosx }{ 1+x^{ 2 } } \) …………. (1)
P = \(\frac { 2x }{ (1+x^{ 2 }) } \), Q = \(\frac { cosx }{ 1+x^{ 2 } } \)
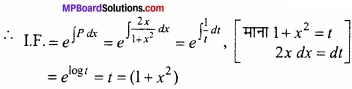
अतः अवकल समी. (1) का अभीष्ट हल है
y.(I.F.) = ∫Q.(I.F.) dx + c
⇒ y(1 + x2) = ∫\(\frac { cosx }{ 1+x^{ 2 } } \) dx + c
⇒ y(1 + x2) = ∫cos x dx + c
⇒ y(1 + x2) = sin x + c
![]()
प्रश्न 6.
किसी वस्तु के बनाने का सीमांत लागत मूल्य c'(x) = \(\frac{dc}{dx}\) = 2 + 0.15 x समीकरण से दिया जाता है। इस वस्तु के बनाने पर कुल लागत मूल्य c(x) ज्ञात कीजिए। (दिया है: c(0) = 100)
हल:
दिया है:
समीकरण c'(x) = \(\frac{dc}{dx}\) = 2 + 0.15 x
समाकलन करने पर,
∫c'(x) dx = ∫(2 + 0.15 x) dx
c(x) = 2x + 0.15 \(\frac { x^{ 2 } }{ 2 } \) + A ………. (1)
अब यदि x = 0 तो
c(0) = 2 × 0 + \(\frac{0.15}{2}\) × o2 + A
⇒ c(0) = A [∵c(0) = 100]
∴ A = 100,
समी. (1) में मान रखने पर,
c(x) = 2x + 0.075 x2 + 100
प्रश्न 7.
अवकल समीकरण x\(\sqrt { 1+y^{ 2 } } \) dx + y \(\sqrt { 1+x^{ 2 } } \) dy = 0 को हल कीजिए।
हल:
दिया गया अवकल समीकरण है:
x\(\sqrt { 1+y^{ 2 } } \) dx + y \(\sqrt { 1+x^{ 2 } } \) dy = 0
⇒ \(\frac { y }{ \sqrt { 1+y^{ 2 } } } \) dy = – \(\frac { x }{ \sqrt { 1+x^{ 2 } } } \)
दोनों पक्षों का समाकलन करने पर,
∫\(\frac { y }{ \sqrt { 1+y^{ 2 } } } \) dy = -∫\(\frac { x }{ \sqrt { 1+x^{ 2 } } } \) dx + c
⇒ \(\sqrt { 1+y^{ 2 } } \) = – \(\sqrt { 1+x^{ 2 } } \) + c
⇒ \(\sqrt { 1+x^{ 2 } } \) + \(\sqrt { 1+y^{ 2 } } \) = c
प्रश्न 8.
अवकल समीकरण हल कीजिए –
(x + y + 1) \(\frac{dy}{dx}\) = 1?
हल:
दिया गया अवकल समीकरण है:
(x + y + 1) \(\frac{dy}{dx}\) = 1
⇒ \(\frac{dx}{dy}\) = x + y + 1
⇒ \(\frac{dx}{dy}\) – x = y + 1
यह y के सापेक्ष x का अवकल समीकरण है।
इसकी तुलना रैखिक अवकल समीकरण \(\frac{dx}{dy}\) + Px = Q से करने पर,
P = – 1 तथा Q = y + 1
![]()
अत: अभीष्ट हल होगा:

![]()
प्रश्न 9.
अवकल समीकरण sec2 x tan y dx + sec2 y tan xdy = 0 को हल कीजिए।
हल:
दिया है:
sec2 xtan ydx + sec2 ytan xdy = 0
⇒ sec2 tan x dy = -sec2 tan ydx
⇒ \(\frac { sec^{ 2 }y }{ tany } \) dy = \(\frac { sec^{ 2 }x }{ tanx } \) dx
⇒ ∫\(\frac { sec^{ 2 }y }{ tany } \) dy = -∫\(\frac { sec^{ 2 }x }{ tanx } \) dx + c
⇒ log y = – log x + log c
⇒ log x + log y = log c
⇒ log xy = log c
⇒ xy = c
प्रश्न 10.
अवकल समीकरण हल कीजिए।
\(\frac{dy}{dx}\) = y tan x – 2 sin x?
हल:
दिया गया अवकल समीकरण
\(\frac{dy}{dx}\) – y tan x = -2 sin x
इसकी तुलना \(\frac{dy}{dx}\) + Py = Q से करने पर,
P = – tan x, Q = – 2 sin x
अभीष्ट हल y.(I.F.) = ∫Q.I.F.dx + c
⇒ y cos x = -2∫sin x cos x dx + c
⇒ y cos x= -∫sin 2x dx + c
⇒ y cos x = \(\frac{cos 2x}{2}\) + c
प्रश्न 11.
अवकल समीकरण \(\frac{dy}{dx}\) + 2y = 4x को हल कीजिए।
हल:
\(\frac{dy}{dx}\) + 2y = 4x
इसकी तुलना \(\frac{dy}{dx}\) + Py = Q से करने पर,
P = 2,Q = 4x

⇒ y = 2x – 1 + c.e-2x
प्रश्न 12.
अवकल समीकरण cos2x \(\frac{dy}{dx}\) + y = 2 को हल कीजिए।
हल:
cos2 x \(\frac{dy}{dx}\) + y = 2
⇒ \(\frac{dy}{dx}\) + sec2 x.y = 2 sec2 x
इसकी तुलना \(\frac{dy}{dx}\) + Py = Q से करने पर,
P = sec2 x, Q = 2 sec2 x

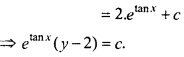
![]()
प्रश्न 13.
अवकल समीकरण cos x \(\frac { dy }{ dx } \) + y = sin x को हल कीजिये।
हल:
cos x \(\frac{dy}{dx}\) + y = sin x
⇒ \(\frac{dy}{dx}\) + secx. y = tan x
इसकी तुलना \(\frac{dy}{dx}\) + Py = Q से करने पर,
P = sec x, Q = tan x

प्रश्न 14.
अवकल समीकरण (1 + y2) dx = (tan-1 y – x) dy को हल कीजिए। (CBSE 2015)
हल:
दिया गया अवकल समीकरण है –
(1 + y2) dx = (tan-1y – x) dy
\(\frac{dx}{dy}\) + \(\frac { x }{ 1+y^{ 2 } } \) = \(\frac { tan^{ -1 }y }{ 1+y^{ 2 } } \)

प्रश्न 15.
अवकल समीकरण (1 + y2) + (x – etan-1 y) \(\frac{dy}{dx}\) = 0 को हल कीजिए। (CBSE 2016)
हल:
दिया गया अवकल समीकरण है –
(1 + y2) + (x – etan-1 y) \(\frac{dy}{dx}\) = 0

समी (1) की तुलना \(\frac{dx}{dy}\) + Px = Q से करने पर,

अतः समीकरण का हल होगा –
x.I.F = ∫I.F. × Qdy
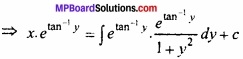
tan-1y = t रखने पर,
\(\frac{d}{dy}\) tan-1 y = \(\frac{dt}{dy}\)
⇒ \(\frac { 1 }{ 1+y^{ 2 } } \) dy = dt
∴ x.etan-1 y = ∫et.et dt = ∫e2t dt
⇒ x.etan-1 y = \(\frac{1}{2}\) e2t + c
⇒ x.etan-1 y = \(\frac{1}{2}\) e2 tan-1 y + c
![]()
प्रश्न 16.
अवकल समीकरण (1 + x2) \(\frac{dy}{dx}\) + 2xy = \(\frac { 1 }{ 1+x^{ 2 } } \) को हल कीजिए, जहाँ y = 0 तथा x = 1(NCERT)
हल:
दिया गया अवकल समीकरण है –
(1 + x2) \(\frac{dy}{dx}\) + 2xy = \(\frac { 1 }{ 1+x^{ 2 } } \)
⇒ \(\frac{dy}{dx}\) + \(\frac { 2xy }{ 1+x^{ 2 } } \) = \(\frac { 1 }{ 1+x^{ 2 } } \) )2
समी. (1) की तुलना \(\frac{dy}{dx}\) + Py = Q से करने पर,
यहाँ P = \(\frac { 2x }{ 1+x^{ 2 } } \), Q = \(\frac { 1 }{ 1+x^{ 2 } } \) )2

अतः समीकरण का हल होगा –
y.I.F. = ∫I.F. × Qdx

y = 0 तथा x = 1 रखने पर,
0(1+1)2 = tan-1 + c
⇒ 0 = \(\frac { \pi }{ 4 } \) + c
⇒ c = – \(\frac { \pi }{ 4 } \)
c का मान समी. (2) में रखने पर, अवकल समीकरण का हल होगा
y.(1 + x2) = tan-1 x – \(\frac { \pi }{ 4 } \)
![]()
प्रश्न 17.
अवकल समीकरण \(\frac{dy}{dx}\) + cot x = 4x cosec x का एक विशिष्ट हल ज्ञात कीजिए। दिया गया है कि – y = 0 तथा x = \(\frac { \pi }{ 2 } \) (NCERT; CBSE 2012)
हल:
दिया गया अवकल समीकरण है –
\(\frac{dy}{dx}\) + y cot x = 4x cosec x
समी. (1) की तुलना \(\frac{dy}{dx}\) + Py = Q से करने पर,
P = cot x, Q = 4x cosecx
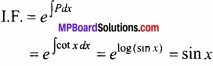
अतः समीकरण का हल होगा –
y.I.F. = ∫1.F. × Qdx
⇒ y.sin x = ∫sin x × 4x cosec x dx
⇒ y sin x = 4∫\(\frac { xsinx }{ sinx } \) dx
⇒ y sin x = 4∫xdx
⇒ y sin x = \(\frac { 4x^{ 2 } }{ 2 } \) + c
⇒ y sin x = 2x2 + c
x = \(\frac { \pi }{ 2 } \) तथा y = 0 रखने पर,
0(sin \(\frac { \pi }{ 2 } \) ) = 2( \(\frac { \pi }{ 2 } \) )2 + c
⇒ 0 = \(\frac { 2\pi ^{ 2 } }{ 4 } \) + c
∴ c = \(\frac { -\pi ^{ 2 } }{ 2 } \)
c का मान समी. (2) में रखने पर, अवकल समीकरण का अभीष्ट हल होगा –
y.sinx = 2x2 – \(\frac { \pi ^{ 2 } }{ 2 } \)