MP Board Class 11th Maths Important Questions Chapter 7 Permutations and Combinations
Permutations and Combinations Important Questions
Permutations and Combinations Objective Type Questions
(A) Choose the correct option :
Question 1.
The correct relation between nPr and nCr is :
(a) nCr = \(\frac{[r}{^{n} P_{r}}\)
(b) nCr.nPr= 1
(c) nCr = \(^{n} P_{r} \times\lfloor r\)
(d) \(^{n} C_{r} \times\left\lfloor r=^{n} P_{r}\right.\)
Answer:
(d) \(^{n} C_{r} \times\left\lfloor r=^{n} P_{r}\right.\)
Question 2.
If nC2:nC4 = 2 : 1, then n = …………..
(a) 3
(b) 4
(c) 5
(d) 6
Answer:
(c) 5
Question 3.
How many words can be made by the letter of the word ‘COMMITEE’:
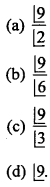
Answer:
![]()
Question 4.
If nP4 = 20 x nP3, then n =
(a) 20
(b) 21
(c) 18
(d) 23
Answer:
(d) 23
![]()
Question 5.
The number of different words that can be formed from the letter of the word ‘TRIANGLE’:
(a) 7200
(b) 36000
(c) 144000
(d) 1240.
Answer:
(b) 36000
Question 6.
In how many ways three person can be seated in 4 chairs :
(a) 42
(b) 20
(c) 24
(d) 12.
Answer:
(c) 24
Question 7.
If 15Cr = 15Cr – 3 , then the value of rC6 will be :
(a) 84
(b) 83
(c) 82
(d) 80.
Answer:
(a) 84
Question 8.
5C0 + 5C1 + 5C2 + 5C3 + 5C4 + 5C5 = ……………..
(a) 30
(b) 32
(c) 23
(d) 42
Answer:
(b) 32
Question 9.
The value of : \(\frac{1}{\lfloor- 4}\) will be :
(a) 0
(b) ∞
(c) 4
(d) 1.
Answer:
(a) 0
Question 10.
If 10Pr = 720, then the value of r will be :
(a) 4
(b) 5
(c) 6
(d) 3
Answer:
(d) 3
(B) Match the following :

Answer:
- (d)
- (a)
- (f)
- (b)
- (c)
- (e)
(C) Fill in the blanks :
- The number of words can be made by the letters of the word ‘INDIA’ ……………
- In order to invite 6 friends, the number of ways to send 3 servant is ……………
- If 20Cr = 20Cy; x ≠ y, then the value of x + y will be ……………
- The numbers of ways greater than 4000 can be made by the digits 2, 4, 5, 7 is ……………
- If 12Pr = 1320, then r will be ……………
- The number of ways can 8 friends be seated in a circular table is ……………
- If nC8 = nC12, then n will be ……………
Answer:
- 60
- 46
- 20
- 48
- 3
- 5040
- 20
(D) Write true / false :
- If nCr + nCr + 1 = n + 1Cx, then x will be 6.
- 5 letters be posted in 4 letter boxes in 54 ways.
- Fruit can be chosen from 5 guavas, 3 apples and 4 mangoes in 60 ways.
- The number of ways can 8 friends stands in a row is 8.
- The value of nCr ÷ n – 1Cris \(\frac { n }{ r – 1 }\)
Answer:
- True
- False
- False
- True
- False.
(E) Write answer in one word / sentence :
- How many four digit numbers can be formed with the digits 2, 3, 4, 5 in these number divisible by 2?
- How many ways can a garland be prepared with 6 flowers?
- If 2.nC5 = 9.n – 2C5, then the value of n will be
- Five points out of 15 points are collinear. If these points be joined, then how many triangles can be formed?
- The value of
 will be?
will be?
Answer:
- 12
- 60
- 10
- 30
- 56C4
Permutations and Combinations Short Answer Type Questions
Question 1.
If \(\frac{1}{\lfloor6}\) + \(\frac{1}{\lfloor7}\) = \(\frac{x}{\lfloor8}\), then find the value of x.
Solution:
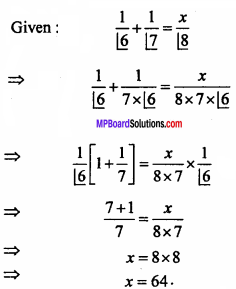
Question 2.
Find the value of
![]()
(i) n = 6, r = 2 (ii) n = 9, r = 5
Solution:

Question 3.
If n-1P3 : nP4 = 1 : 9, then find the value of n.
Solution:
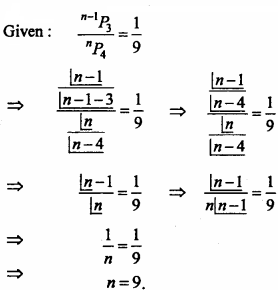
Question 4.
IF nP5 : 42.nP3, then find the value of n.
Solution:
IF nP5 = 42.nP3, then find the value of n.
Solution:
Given: nP5 = 42.nP3
⇒ n(n – 1)(n – 2)(n – 3)(n – 4) = 42n(n – 1)(n – 2)
⇒ (n – 3)(n – 4) = 42
⇒ n2 – 7n – 30 = 0
⇒ n2 – 10n + 3n – 30 = 00
⇒ (n – 10) (n + 3) = 0
n = 10, n ≠ – 3.
Question 5.
IF \(\frac{^{n} P_{4}}{^{n-1} P_{4}}\) = \(\frac { 5 }{ 3 }\), then find the value of n.
Solution:
Given : \(\frac{^{n} P_{4}}{^{n-1} P_{4}}\) = \(\frac { 5 }{ 3 }\)
⇒ 3.nP3 = 5.n-1P4
⇒ 3n(n – 1)(n – 2)(n – 3) = 5 (n – 1)(n – 2)(n – 3)(n – 4)
⇒ 3n = 5 (n – 4)
⇒ n = 10.
Question 6.
If nC9 = nC8, then find the value of nC17.
Solution:
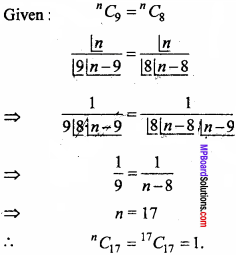
Question 7.
If nPn-2 = 60, then find the value of n.
Solution:
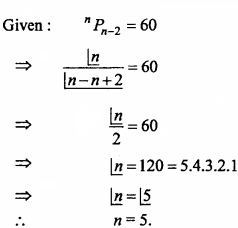
Question 8.
If 12Pr = 1320, then find the value of r.
Solution:

Question 9.
If nC14 = nC16, then find the value of 32Cn.
Solution:
Given : nC14 = nC16
⇒ nC14 = nC16-1
⇒ 14 = n – 16
⇒ n = 30
∴ 32Cn = 32C30 = 32C2
= \(\frac { 32.31 }{ 2 }\) = 496.
Question 10.
If 20Cx = 20Cy, then find the value of x + y.
Solution:
Given :
⇒ 20Cx = 20Cy
⇒ 20Cx = 20C20-y
⇒ x = 20 – y
⇒ x + y = 20
![]()
Question 11.
In how many ways can 8 friends sit around a round table?
Solution:
Total number of ways of sitting 8 friends around table = \(\lfloor 8 – 1\) = \(\lfloor 7\)
= 7 x 6 x 5 x 4 x 3 x 2 x 1
= 5040.
Question 12.
In how many ways can a garland be prepared with 6 flowers?
Solution:
Ways of preparing the garlands with 6 flowers = \(\frac { 1 }{ 2 }\) \(\lfloor 6 – 1\)
= \(\frac { 1 }{ 2 }\) \(\lfloor 5\)
= \(\frac { 1 }{ 2 }\).5.4.3.2.1 = 60.
Question 13.
How many numbers between 100 and 1000 can be formed with the digits 2, 3, 0, 4, 8, 9 if repetition of digits is not allowed in the same number?
Solution:
The numbers between 100 and 1000 are of three digits.
∴Number of three digits made from 6 digits will be 6P3.
In this number which begins with 0 will be 5P2.
∴Required number = 20Cy – 5P2 = 120 – 20 = 100.
Question 14.
How many words, with or without meaning can be formed using all the letters of the word EQUATION? (NCERT)
Solution:
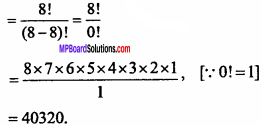
Question 15.
How many chords can be drawn through 21 points on a circle? (NCERT)
Solution:
By joining two points we get one chord.
∴ No. of chords = 21C2
= \(\frac { 21 x 20 }{ 2 x 1 }\)
= 210.
Question 16.
In how many ways can a team of 3 boys and 3 girls can be selected from 5 boys and 4 girls? (NCERT)
Solution:
Number of ways of selecting 3 boys from 5 boys and 3 girls from 4 girls will be
= 5C3 × 4C3
= \(\frac { 5 × 4 × 3 }{ 3 × 2 × 1}\) × \(\frac { 4 × 3 × 2 }{ 3 × 2 × 1 }\)
= 10 x 4 = 40.
Permutations and Combinations Long Answers Type Questions
Question 1.
Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each colour. (NCERT)
Solution:
Since, 3 red balls out of 6 red balls can be selected
= 6C3 = \(\frac { 6 × 5 × 4 }{ 3 × 2 × 1}\) = 20
3 white balls out of 5 white balls = 5C3 = \(\frac { 5 × 4 × 3 }{ 3 × 2 × 1}\) = 10
and 3 blue balls out of 5 blue balls = 5C3 = \(\frac { 5 × 4 × 3 }{ 3 × 2 × 1}\) = 10
Total number of ways of selecting 9 balls = 20 x 10 x 10
Question 2.
Determine the number of 5 cards combinations out of a deck of 52 cards, if there is exactly one ace in each combination (NCERT)
Solution:
Number of ways of selecting one ace from 4 ace = 4C1
Number of selecting 4 cards from 48 cards = 48C4
= \(\frac { 48 × 47 × 46 × 45 }{ 4 × 3 × 2 × 1}\)
Total number of ways = 4C1 x 48C4
= 4 × = \(\frac { 48 × 47 × 46 × 45 }{ 4 × 3 × 2 × 1}\)
= 7, 78, 320.
![]()
Question 3.
In how many ways can one select a cricket team of eleven players from 17 players. In which only 5 players can bowl, if each cricket team of 11 must include exactly 4 bowlers? (NCERT)
Solution:
Out of 17 players, to select 11 players in which 5 bowlers and 12 batsman.
Out of 5 bowlers to select 4 bowlers = 5C4 = 5
Out of 12 batsman to select 7 batsman = 12C7
= \(\frac { 12 × 11 × 10 × 9 × 8 × 7 × 6 }{ 7 × 6 × 5 × 4 × 3 × 2 × 1 }\)
= 11 × 9 × 8 = 792
∴ Number of ways selecting 11 players = 5 x 792 = 3960.
Question 4.
A bag contains 5 black and 6 red balls, determine the number of ways in which 2 black and 3 red balls can be selected. (NCERT)
Solution:
There are 5 black and 6 red balls.
Out of 5 black balls, 2 black balls can be =5C2 = \(\frac { 5 × 4 }{ 2 × 1 }\) = 10
Out of 6 red balls, 3 red balls can be = 6C3 = \(\frac { 6 × 5 × 4 }{ 3 × 2 × 1 }\) = 20
∴ Total No. of ways = 10 x 20 = 200.
Question 5.
In how many ways can a student choose a program of 5 courses, if 9 courses are available and 2 specific courses are compulsory for each students? (NCERT)
Solution:
Number of available courses = 9.
Number of courses to choose = 5.
Compulsory courses = 2.
∴ Required number of ways = 9-2C5-2 = 7C3
= \(\frac { 7 × 6 × 5 }{ 3 × 2 × 1 }\) = 35.
Question 6.
How many words, with or without meaning each of 2 vowels and 3 consonants can be formed from the letters of the word DAUGHTER? (NCERT)
Solution:
There are 3 vowels and 5 consonants in DAUGHTER.
2 vowels out of 3 vowels = 3C2 = \(\frac { 3! }{ 1!2! }\) = \(\frac { 3 × 2 }{ 2 × 1 }\)
3 consonants out of 5 consonats = 5C3 = \(\frac { 5! }{ 2!3! }\) = \(\frac { 5 × 4 × 3 }{ 3 × 2 × 1 }\) = 10
Arrangement of 2 vowels and 3 consonants = 5!
= 5 × 4 × 3 × 2 × 1 = 120
Question 7.
How many words, with or without menning can be formed using all the letters of the word EQUATION at a time so that the vowels and consonants occur together?
Solution:
Given word is EQUATION.
Vowels – E, U, A, I, O
Consonants – T, Q, N.
Arrangement of 5 vowels = 5! = 5 x 4 x 3 x 2 x 1 = 120
Arrangement of 3 consonants = 3! = 3 x 2 x 1 = 6
Arrangements of vowels and consonants = 2!
∴ Total No. of ways = 120 x 6 x 2! = 720 x 2 = 1440.
![]()
Question 8.
A committee of 7 members has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of: (NCERT)
- Exactly 3 girls
- At least 3 girls
- At most 3 girls.
Solution:
Total members in committee = 7
1. Selection of 3 girls and 4 boys in committee
= 4C3 x 9C4
= \(\frac { 4 × 3 × 2 × 1 }{ 3 × 2 × 1 }\) x \(\frac { 9 × 8 × 7 × 6 }{ 4 × 3 × 2 × 1 }\)
= 9 x 8 x 7 = 504.
2. Selection of minimum 3 girls in committee
= 4C3 x 9C4 + 4C4 x 9C3
= 504 + 1 x \(\frac { 9 × 8 × 7 }{ 3 × 2 × 1 }\) = 504 + 84 = 588.
3. Selection of maximum 3 girls in a committee

Question 9.
How many different words can be formed by using the letters of the word ALLAHABAD, out of which in how many words vowels will come in even places? (NCERT)
Solution:
Total number of letters in ALLAHABAD = 9.
In which A = 4 times, L = 2 times.
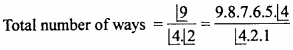
= 9.8.7.3.5 = 7560.
Number of even places are = 4 and odd places = 5. Hence we can put A only in 4 places and rest 5 letters L, L, H, B, D in 5 odd places in![]() ways.
ways.

Question 10.
In how many ways can a cricket team of eleven can be formed from 14 players? Which win always have :
- Captain is always taken.
- When two fast bowlers are always taken?
Solution:
1. When captain is always taken (11 – 1) from (14 – 1) players.
= 13C10 = 13C3
= \(\frac { 13.12.11 }{ 3.2.1 }\) = 286.
2. When two fast bowlers are always taken = 12C9 = 12C3
= \(\frac { 12.11.10 }{ 3.2.1}\)
Question 11.
In how many ways committee of 5 members can be formed out of 6 men and 4 women ? If the committee has : (i) Only one woman, (ii) At least one woman.
Solution:
(i) Only one woman out of 4 women and 4 men out of 6 men.
No. of ways = 6C4 x 4C1
= 6C2 x 4
= \(\frac { 6 × 5 × 4 }{ 2.1 }\) = 60
(ii) Atleast one woman :

Hence, total No. of ways = 60 + 120 + 60 + 6 = 246.
Question 12.
If 2nC3 : nC2 = 12 : 1,then find the value of it. (NCERT)
Solution:

Question 13.
If 2nC3 : nC3 = 11 : 1, then find the value of it. (NCERT)
Solution:
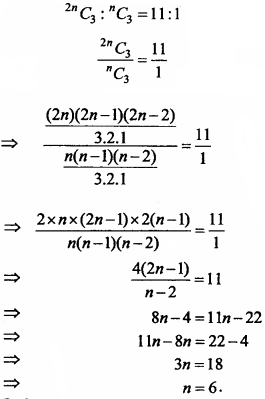
Question 14.
Prove that:
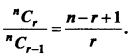
Solution:

Question 15.
Prove that:
2nPn = 2n{1.3.5 …………. (2n – 1)}.
Solution:
