MP Board Class 11th Maths Important Questions Chapter 6 Linear Inequalities
Linear Inequalities Important Questions
Linear Inequalities Objective Type Questions
(A) Choose the correct option :
Question 1.
If x is a real number, then the solution of inequality 3x + 1 < 5x + 7 is :
(a) (- ∞, 3)
(b) (- 3,∞)
(c) (3, ∞)
(d) None of these.
Answer:
(b) (- 3,∞)
Question 2.
If x is a real number, then the solution of inequality \(\frac { 1 }{ 2 }\) (3x – 1) ≥ \(\frac { 1 }{ 3 }\)(4x + 3) – 1 is :
(a) (- ∞, 3)
(b) (3, ∞)
(c) (3, ∞)
(d) None of these.
Answer:
(c) (3, ∞)
Question 3.
The graph of x ≤ 2 and y ≥ 2 is situated in the :
(a) First and second quadrant
(b) Second and Third quadrant
(c) First and third quadrant
(d) None of these.
Answer:
(a) First and second quadrant
Question 4.
In linear programming problems, the objective function will be :
(a) One of the constraints
(b) A linear function which gives optimum solution
(c) Relation between varivable
(d) None of these.
Answer:
(b) A linear function which gives optimum solution
![]()
Question 5.
In linear constraints the maximum value of objective function will be :
(a) At the centre of feasible region
(b) At (0, 0)
(c) At one of the vertices of the feasible region
(d) At the vertex which is situated at maximum distance from (0, 0)
Answer:
(c) At one of the vertices of the feasible region
Question 6.
Which word is not used in linear programming problems :
(a) Slack variable
(b) Objective function
(c) Concave region
(d) Feasible solution.
Answer:
(a) Slack variable
Question 7.
The minimum value of p = 6x + 16y when constraints are x ≤ 40 and y ≥ 20 and x, y ≥ 0 is :
(a) 240
(b) 320
(c) 0
(d) None of these.
Answer:
(b) 320
Question 8.
At which point the value of 3x + 2y is maximum under the constraints x + y ≤ 2, x ≥ 0 y ≥ 0 :
(a) (0, 0)
(b) (1.5, 1.5)
(c) (2, 0)
(d) (0, 2).
Answer:
(c) (2, 0)
Question 9.
Under constraints x ≥ 0, y ≥ 0, x + y ≤ 4, maximum value of P = 3x + y is :
(a) 8
(b) 12
(c) 6
(d) 10.
Answer:
(b) 12
Question 10.
Under constraints x – 2y ≥ 6, x + 2y ≥ 0, x ≤ 6 , maximum value of P = x + 3y is :
(a) 16
(b) 17
(c) 18
(d) 19.
Answer:
(c) 18
Question 11.
Feasible solution of linear programming is in :
(a) Second quadrant only
(b) First and third quadrant
(c) First and second quadrant
(d) First quadrant only.
Answer:
(d) First quadrant only.
Question 12.
If x is a real number and |x| < 4, then :
(a) x ≥ 4
(b) – 4 < x < 4
(c) x ≤ – 4
(d) – 4 ≤ x ≤ 4
Answer:
(b) – 4 < x < 4
Question 13.
Solution of inequality 3x – 2 < 0 will be :
(a) [3, ∞]
(b) [- ∞, \(\frac { 2 }{ 3 }\)]
(c) [3, 2]
(d) [2, 3]
Answer:
(b) [- ∞, \(\frac { 2 }{ 3 }\)]
Question 14.
The set of solutions of inequality 4x – 12 ≥ 0 is :
(a) (4, 2)
(b) [4, 12]
(c) [3, ∞]
(d) [3, ∞]
Answer:
(c) [3, ∞]
![]()
Question 15.
The solution of inequality |4x – 3| < 27 is :
(a) (- 6, \(\frac { 15 }{ 2 }\))
(b) [ – 6, \(\frac { 15 }{ 2 }\) ]
(c) [ – 6, \(\frac { 15 }{ 2 }\) )
(d) ( – 6, \(\frac { 15 }{ 2 }\) ]
Answer:
(a) (- 6, \(\frac { 15 }{ 2 }\))
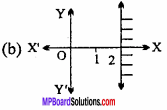
Question 16.
Solution of inequality x > 2 is :
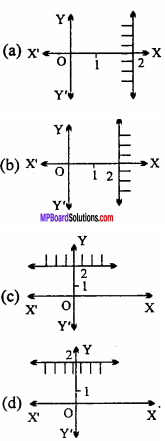
Answer:
Question 17.
Sawant has a space to store at most 13 boxes of apples and oranges. If he bought x boxes of oranges and y boxes of apples, then correct inequality will be :
(a) x + y < 13
(b) x + y > 13
(c) x + y < 13
(d) x + y = 13.
Answer:
(c) x + y < 13
Question 18.
In which point the maximum of objective function P = 10x + 6y in the following points:
(a) (0, 0)
(b) (8, 4)
(c) (10, 0)
(d) (0, 0).
Answer:
(b) (8, 4)
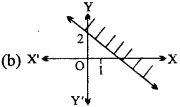
Question 19.
The graph of inequality x +y > 2 is :
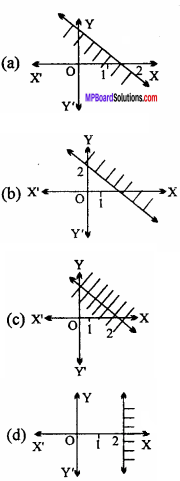
Answer:
Question 20.
The solution of inequality 3x – 7 ≥ x + 1 is :
(a) [4, ∞]
(b) (4, ∞]
(c) (4, ∞)
(d) [4, ∞).
Answer:
(d) [4, ∞).
Question 21.
The solution of inequality 3x – 6 > 0; 2x – 6 > 0 is :
(a) [3, ∞]
(b) (3, ∞)
(c) [2, ∞)
(d) (2, ∞).
Answer:
(b) (3, ∞)
Question 22.
The solution of inequality 2x + 6 = 0; 4x – 8 < 0 is :
(a) [- 3, ∞)
(b) (3, 2)
(c) [- 3, 2)
(d)[- 3, 2].
Answer:
(c) [- 3, 2)
![]()
Question 23.
The set of solution of inequality x ≥ 0 is :
(a) All points of X – axis and first, fourth quadrants
(b) All points of first and fourth quadrants
(c) All points of first and second quadrants
(d) All points of Y – axis and first, fourth quadrants.
Answer:
(d) All points of Y – axis and first, fourth quadrants.
Question 24.
Variables of the objective function of linear Programming problem are :
(a) Negative
(b) Zero or Negative
(c) Zero
(d) Zero or Positive.
Answer:
(d) Zero or Positive.
(B) Match the following :
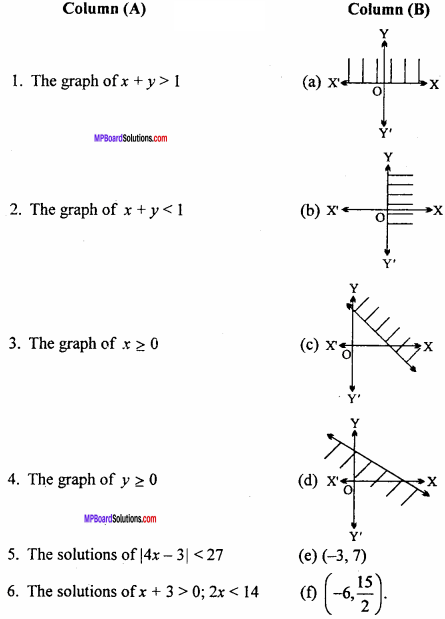
Answer:
- (c)
- (d)
- (a)
- (f)
- (e)
(C) Fill in the blanks :
- The maximum or minimum value of objective function is called ……………….
- The graph of x ≥ 0 is situated in the ………………. quadrant.
- The graph of y ≤ 0 is situated in the ………………. quadrant.
- Solution of inequality 3x + 1 < 5x + 7 is (where x is an integer) ……………….
- Solution of inequality 3x – 4 < 5 is (where x is an integer) ……………….
- Solution of inequality 4x + 3 > – 13 is (where x is a real number) ……………….
- Solution of inequality 7x – 2 < 5x + 4 is (where x is a real number) ……………….
- Solution of inequality 20x < 90 is (where x is a natural number) ……………….
- Solution of inequality 3x – 2 < x + 4 is ……………….
- The inequality of one variable is ……………….
- The set of solutions of y > 0 are in the ………………. and ………………. quadrant.
- x ≥ 2 and y ≥ 2 will be situated in the graph ……………….
- The domain of inequality 3x – 15 ≤ 0 is ……………….
- A function whose maximum and minimum value is to be found subject to the given constrains is known as ……………….
Answer:
- Optimum value
- First and fourth
- Third and fourth
- (- 3, ∞)
- {… – 3, – 2, -1, 0, 1, 2}
- (- 4, ∞)
- (- ∞, 3)
- {1, 2, 3, 4}
- (- ∞, 3)
- ax + b ≥ c or ax + b ≤ c; where a ≠ 0
- First and second
- First and second quadrant
- (- ∞, \(\frac { 15 }{ 3 }\))
- Objective function
(D) Write true / false :
- If the variable x is such that its value lies between two fixed point a and b, then {x : a < x < b} is called a closed interval.
- The function whose maximum or minimum value is to be found is called objective function.
- The set of values of the variable satisfying all constraint is called feasible solution of the problem.
- The process of doing certain specified steps in a given order is called programming.
- The set {x : a < x < b} which consists of both a and b is called open interval.
- The solution of inequality 6x – 30 ≥ 0 will be x ≤ 5
- The solution of inequality – 2x + 7 < – 13 will be (10, ∞).
- The linear inequality of one variable is ax + b = 0; a ≠ 0, ∀a, b ∈
- R. The line inequality of two variables is ax + by + c = 0; a ≠ 0, b ≠ 0, ∀a, b, c ∈ R.
- The graph of inequality x > 0 is :
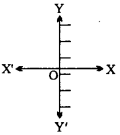
- The graph of inequality y ≤ 0 is :
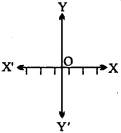
- The solution of inequality 5x – 30 ≤ 0 is :

Answer:
- False
- True
- True
- True
- False
- False
- True
- True
- True
- True
- True
- False.
(E) Write answer in one word / sentence :
- In which quadrant lies the solution of x ≥ 0 and y ≥ 0?
- In which quadrant lies the solution of x ≤ 2 and y ≥ 2?
- Write the solution of 3(2 – x) ≥ 2(1 – x) .
- Write the solution of \(\frac { x }{ 3 }\) > \(\frac { x }{ 2 }\) + 1.
- Write the solution of \(\frac { x – 4 }{ x + 2 }\) ≤ 2.
Answer:
- First quadrant
- First and second quadrant
- (- ∞, 4]
- (- ∞, – 6)
- (- ∞, – 8]∪(- 2, ∞)
Linear Inequalities Long Answer Type Questions
Question 1.
Draw the graph of inequality 2x + y ≥ 6 in two – dimensional plane. (NCERT)
Solution:
Given inequality is 2 x + y ≥ 6
Consider this as an equation 2x + y = 6.
For this equation following values of x and y are given in the table :
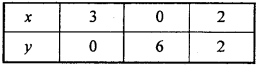
Plot the graph using the above table. Take a point (0, 0) and put in given inequality,
2x + y ≥ 6
⇒ 2 x 0 + 0 ≥ 6
⇒ 0 ≥ 6 Which is false.
Hence, shaded portion will be opposite of origin.
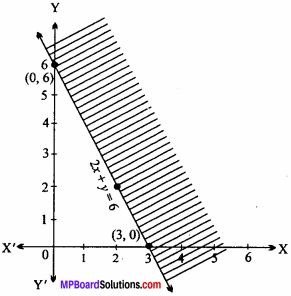
∴ The shaded region represents the inequality 2x + y ≥ 6.
Question 2.
Draw the graph of inequality 3x + 4y ≤ 12 in two – dimensional plane. (NCERT)
Solution:
Given inequality : 3x + 4y = 12
Consider this as an equation 3x + 4y = 12.
For this equation the following values of x and y are given in the table :
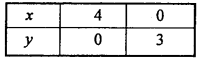
Plot the above points in a graph paper and join them.
Put (0, 0) in given inequality,
⇒ 3x + 4y ≤ 12
⇒ 3 x 0 + 4 x 0 ≤ 12
⇒ 0 ≤ 12
Which is true.
Hence, shaded portion will be towards origin as shown in figure.

∴ The shaded region represents the inequality 3x + 4y ≤ 12
Question 3.
Draw the graph of inequality y + 8 ≥ 2x in two – dimensional plane. (NCERT)
Solution:
Given inequality : y+8 > 2x Consider this as an equation 2x – y = 8
For this equation following values of x and y are given in the table :
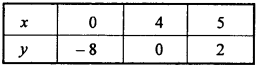
Plot the above points in graph paper and join them.
Put (0, 0) in the given inequality,
y + 8 ≥ 2x
⇒ 0 + 8 ≥ 2 x 0
⇒ 8 ≥ 0 Which is true.
Hence, the shaded portion will be towards origin.
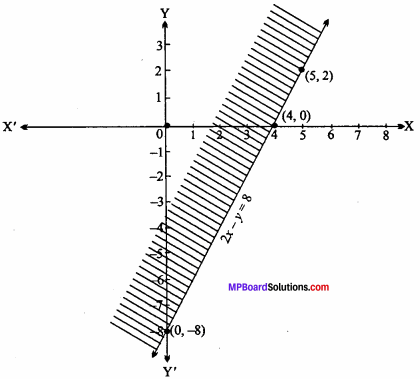
∴ Shaded portion represents the inequality y + 8 ≥ 2x.
Draw the graph of following inequality in two – dimensional plane :
Question 4.
2x – 3y > 6.
Solution:
Given inequality is :
2x – 3y > 6
Consider this as an equation 2x – 3y = 6
Following table is prepared for different values of x and y :
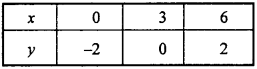
Plot the above points on xy – plane and join them.
Put x = 0, y = 0 in given inequality,
2x – 3y > 6
⇒ 2 x 0 – 3 x 0 > 6
⇒ 0 > 6 Which is false.
Hence, the shaded portion will be opposite of origin.
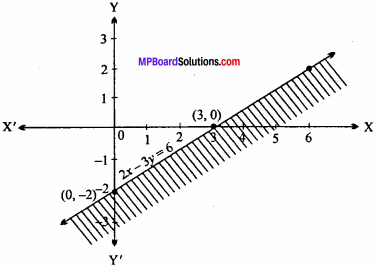
∴The shaded region represents the inequality 2x – 3y > 6
Question 5.
– 3x + 2y ≥ – 6.
Solution:
Given inequality is : – 3x + 2y ≥ – 6.
Consider this as an equation – 3x + 2y = – 6.
Following table is prepared for different values of x and y :
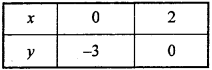
Plotting the above points on xy – plane and join them. Put x = 0, y = 0 in given inequality,
– 3x + 2y ≥ – 6
⇒ – 3(0) + 2(0) ≥ – 6
⇒ 0 ≥ – 6 Which is true.
∴ Shaded portion will be towards origin.
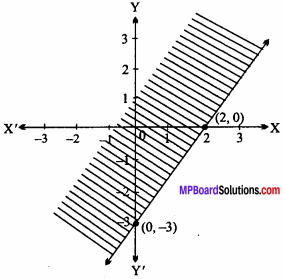
Hence, the shaded portion represents the inequality – 3x + 2y ≥ – 6.
Question 6.
3y – 5x < 30.
Solution:
Given inequality: y – 5x < 30.
Consider this as an equation 3y – 5x = 30.
Following table is prepared for different values of x and y :
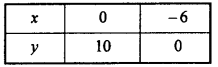
Ploting the above points on xy – plane and join them.
Put x = 0, y = 0 in given inequality,
3y – 5x < 30
⇒ 3(0) – 5(0) < 30
⇒ 0 < 30
Which is true.
Hence, the shaded region will be towards origin.
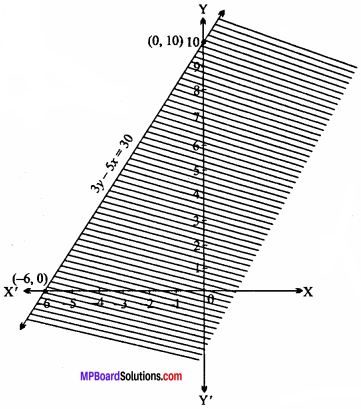
∴ Shaded region represents the inequality 3y – 5x < 30
Question 7.
2x + y ≥ 6, 3x + 4y ≤ 12. (NCERT)
Solution:
Given inequalities are :
2x + y ≥ 6
and 3x + 4y ≤ 12
For the equation 2x+y = 6.
Following table is prepared for different values of x and y :
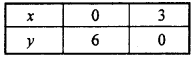
Plotting the above points on xy – plane to get straight line.
Put x = 0, y = 0 in the inequality,
2x + y ≥ 6
⇒ 2 x 0 + 0 ≥ 6
⇒ 0 ≥ 6
Which is false.
∴ The shaded region will be opposite of origin.
For the equation 3x + 4y = 12.
Following table is prepared for different values of x and y :
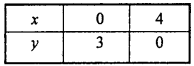
Plotting the above points on xy – plane to get straight line.
Put x = 0, y = 0 in given inequality,
3x + 4y ≤ 12
⇒ 3 x (0) + 4(0) ≤ 12
⇒ 0 ≤ 12
Which is true.
Hence, the shaded portion will be towards origin.
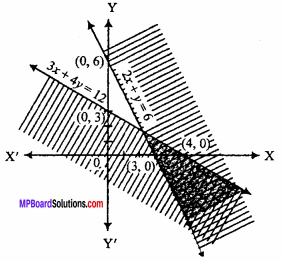
∴ The common shaded region is the required solution of the given inequalities.
Question 8.
Solve the following inequalities graphically in two – dimensional plane : x + y ≥ 4, 2x – y >0. (NCERT)
Solution:
Given inequalities are :
x + y ≥ 4
and 2x – y > 0
For the equation x + y = 4, following table is prepared for different values of x and y:

Plotting the above points on xy – plane to get straight line.
Put x = 0, y = 0 in the inequality,
x + y ≥ 4
⇒ 0 + 0 ≥ 4
⇒ 0 ≥ 4
Which is false.
Hence, the shaded region will be opposite of origin.
Preparing table for different value of x and y of the equation 2x – y = 0 :

Plotting the above points in xy – plane to get straight line.
Put x = 1 and y = 0 in given inequality,
2x – y > 0
⇒ 2(1) – 0 > 0
⇒ 2 > 0
Which is true.
Hence, the shaded region will be towards of point (1,0).
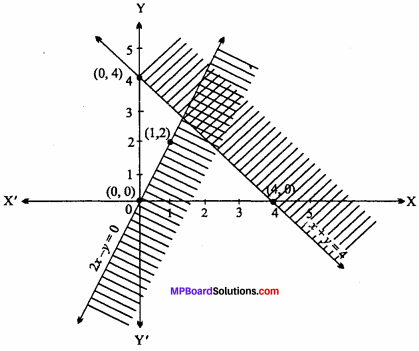
The common shaded region is the required solution of the given inequalities.
Question 9.
Solve the following inequalities graphically in two – dimensional plane :
5x + 4y ≤ 20, x ≥ 1, y ≥ 2 (NCERT)
Solution:
The given inequalities are :
5x + 4y ≤ 20
x ≥ 1
y ≥ 2
Prepared table for different values of x and y of the equation 5x +4y = 20 :
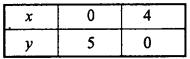
Plotting the points of the above table on xy – plane to get straight line.
Then, put x = 0, y = 0 in the inequality,
5x + 4y ≤ 20
⇒ 0 + 0 ≤ 20
⇒ 0 < 20
Which is true.
∴Shaded region will be towards origin.
For equation x + O.y = 1 to get different values of x and y are in the table :
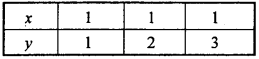
Plotting the points from table on xy plane to get straight line.
Putting x = 0, y = 0 in the inequality,
x ≥ 1
⇒ 0 ≥ 1
Which is false.
Hence, the shaded region will be opposite side of origin.
For equation 0.x + y = 2, the different values of x and y are given in the table :
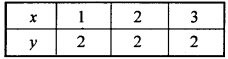
Plotting the points on xy plane to get straight line.
Then, put x = 0, y = 0 (0,0) in the inequality,
y ≥ 2
⇒ 0 ≥ 2
Which is false.
Hence, the shaded region will be opposite side of origin.
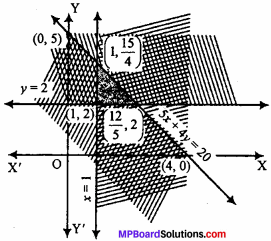
∴ The common shaded region is the required solution of the given inequalities.
Question 10.
Solve the following inequalities graphically :
3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0. (NCERT)
Solution:
The given inequalities are :
3x + 4y ≤ 60
x + 3y ≤ 30
x ≥ 0
y ≥ 0
Prepared table for values of x and y of equation 3x + 4y = 60 :
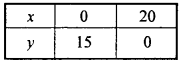
Plotting the above points on xy – plane to get straight line.
Then, put x = 0, y = 0 in the inequality,
3x + 4y ≤ 60
⇒ 0 + 0 ≤ 60
⇒ 0 ≤ 60
Which is true.
Hence, the shaded portion will be towards origin.
Prepared table for values of x and y of equation x + 3y = 30:
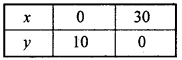
Plotting the above points on xy – plane to get straight line.
Then, put x = 0, y = 0 in the inequality,
x + 3y ≤ 30
⇒ 0 + 0 ≤ 30
⇒ 0 ≤ 30
Which is true.
Hence, the shaded region will be towards origin.
The graph of x = 0 is y – axis and graph of y = 0 is x – axis.
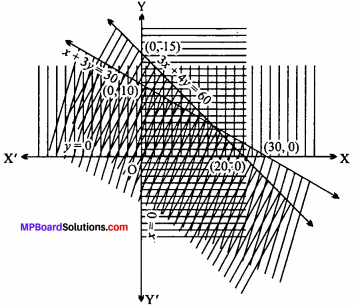
The common shaded region is the required solution set of the given inequalities.