In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग Ex 9.1 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग Ex 9.1
प्रश्न 1.
सर्कस का एक कलाकार एक 20 m लम्बी डोर पर चढ़ रहा है, जो अच्छी तरह से तनी हुई है और भूमि पर सीधे लगे खम्भे के शिखर से बँधा हुआ है। यदि भूमि स्तर के साथ डोर द्वारा बनाया गया कोण 30° का हो, तो खम्भे की ऊँचाई ज्ञात कीजिए। (देखिए संलग्न आकृति : 9.3)
हल :
∆ABC में ∠B समकोण है एवं कोण C = 30° तथा डोरी की लम्बाई AC = 20 m (दिया हुआ है) चूँकि
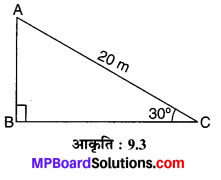
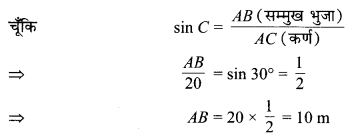
अतः, खम्भे की अभीष्ट ऊँचाई = 10 m है।
प्रश्न 2.
आँधी आने से एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है कि पेड़ का शिखर जमीन को छूने लगता है और इसके साथ 30° का कोण बनाता है। पेड़ के पाद-बिन्दु की दूरी, जहाँ पेड़ का शिखर जमीन को छूता है, 8 m है। पेड़ की ऊँचाई ज्ञात कीजिए।
हल :
मान लीजिए एक पेड़ PQ = h m लम्बा आँधी के कारण QR = x m की ऊँचाई पर स्थित R बिन्दु से टूट जाता है तथा इसका शीर्ष P पृथ्वी पर बिन्दु S पर टिक जाता है तथा पेड़ का यह भाग पृथ्वी के साथ ∠RSQ = 30° का कोण बनाता है तथा इस भाग की लम्बाई SR = PR = (h – x) m होगी अब समकोण ∆RQS में,
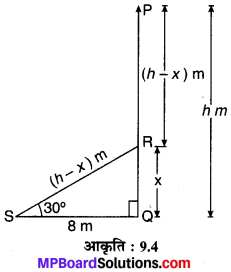
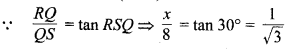

समीकरण (1) से \(x=\frac{8}{\sqrt{3}}\) का मान समीकरण (2) में रखने पर,
![]()
अतः, पेड की अभीष्ट ऊँचाई = 8√3 m है।
प्रश्न 3.
एक ठेकेदार बच्चों को खेलने के लिए एक पार्क में दो फिसलन-पट्टी लगाना चाहती है। 5 वर्ष से कम उम्र के बच्चों के लिए वह एक ऐसी फिसलन पट्टी लगाना चाहती है जिसका शिखर 1.5 m की ऊँचाई पर हो और भूमि के साथ 30° के कोण पर झुका हुआ हो, जबकि इससे अधिक उम्र के बच्चों के लिए वह 3 m की ऊँचाई पर एक अधिक ढाल की फिसलनपट्टी लगाना चाहती है, जो भूमि के साथ 60° का कोण बनाती है। प्रत्येक स्थिति में फिसलन-पट्टी की लम्बाई क्या होनी चाहिए?
हल:
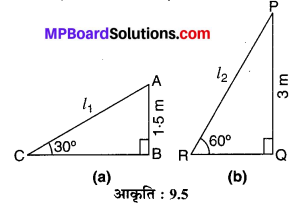
मान लीजिए 5 वर्ष से कम उम्र की बच्चों के लिए AC = l1, m की लम्बाई की फिसलन-पट्टी लगायी जाती है जिसका शिखर A, AB = 1.5 m ऊँचाई पर है तथा फिसलन-पट्टी पृथ्वी के साथ ∠ACB = 30° का कोण बनाती है। [देखिए आकृति 9.5 (a)]
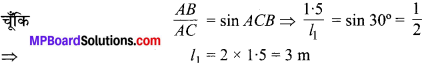
अतः, छोटी फिसलन-पट्टी की अभीष्ट लम्बाई = 3 m है।
अब मान लीजिए 5 वर्ष से अधिक उम्र के बच्चों के लिए PR = l2, m की लम्बाई की फिसलनपट्टी लगायी जाती है जिसका शिखर P, PQ = 3 m की ऊँचाई पर है तथा यह फिसलन-पट्टी पृथ्वी के साथ ∠PRQ = 60° का कोण बनाती है। [देखिए आकृति : 9.5 (b)]
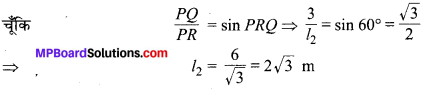
अतः, बड़ी फिसलन-पट्टी की अभीष्ट लम्बाई = 2√3 m है।
प्रश्न 4.
भूमि के एक बिन्दु से, जो मीनार के पाद-बिन्दु से 30 m की दूरी पर है, मीनार के शिखर का उन्नयन कोण 30° है। मीनार की ऊँचाई ज्ञात कीजिए।
हल :
मान लीजिए PQ एक दी हुई मीनार है जिसकी ऊँचाई PQ = h m है तथा इसके पाद बिन्दु Q से QR = 30 m की दूरी पर स्थित बिन्दु R पर मीनार के शिखर P का उन्नयन कोण ∠PRQ = 30° है। (देखिए आकृति 9.6)
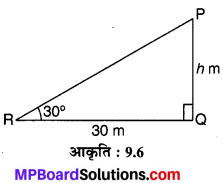

अतः, मीनार की अभीष्ट ऊँचाई = 10√3 m है।
![]()
प्रश्न 5.
भूमि से 60 m की ऊँचाई पर एक पतंग उड़ रही है। पतंग में लगी डोरी को अस्थायी रूप से भूमि के एक बिन्दु से बाँध दिया गया है। भूमि के साथ डोरी का झुकाव 60° है। यह मानकर कि डोरी में कोई ढील नहीं है, डोरी की लम्बाई ज्ञात कीजिए।
हल :
मान लीजिए PR = l m की लम्बाई वाली एक डोरी के सिरे P पर एक पतंग है तथा इसका दूसरा सिरा बिन्दु R पर खूटे से बँधा है।
पतंग की पृथ्वी से ऊँचाई PQ = 60 m है। डोरी पृथ्वी के साथ ∠PRQ = 60° का कोण बनाती है (देखिए आकृति 9.7)।
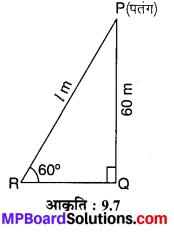

अतः, डोरी की अभीष्ट लम्बाई = 40√3 m है।
प्रश्न 6.
1.5 m लम्बा एक लड़का 30 m ऊँचे एक भवन से कुछ दूरी पर खड़ा है। जब वह ऊँचे भवन की ओर जाता है, तब उसकी आँख से भवन के शिखर का उन्नयन कोण 30° से 60° हो जाता है। बताइए कि वह भवन की ओर कितनी दूरी तक चलकर गया है ?
हल :
मान लीजिए PQ = 30 m ऊँचा एक भवन है। एक लड़का AB = 1.5 m ऊँचाई का पृथ्वी पर बिन्दु B पर खड़ा है। लड़के के नेत्रों से जाने वाली क्षैतिज रेखा PQ को बिन्दु R पर प्रतिच्छेद करती है, जहाँ RQ = AB = 1.5 m
⇒ PR = PQ – RQ = 30 m – 1.5 m
= 28.5m
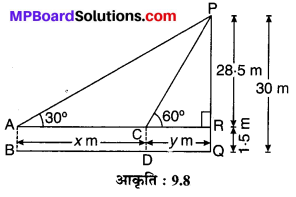
इस स्थिति में P का उन्नयन ∠PAR = 30° और मान लीजिए यह लड़का भवन की ओर x m चलकर CD स्थिति में आ जाता है, जहाँ P का उन्नयन कोण ∠PCR = 60° हो जाता है। यदि CR = y m हो (देखिए आकृति 9.8)
तो समकोण ∆PRC में,

एवं समकोण ∆PRA में,
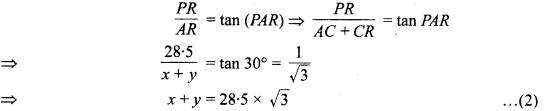
समीकरण (1) से y का मान समीकरण (2) में रखने पर,

अतः, लड़के द्वारा चली गयी अभीष्ट दूरी = 19√3 m है।
प्रश्न 7.
भूमि के एक बिन्दु से एक 20 m ऊँचे भवन के शिखर पर लगी एक संचार मीनार के तल और शिखर के उन्नयन कोण क्रमश: 45° और 60° हैं। मीनार की ऊँचाई ज्ञात कीजिए।
हल :
मान लीजिए एक भवन PQ = 20 मी ऊँचाई का दिया है जिसके ऊपर PR एक संचार मीनार लगा है। बिन्दु S के मीनार के तल एवं शिखर R के उन्नयन कोण क्रमशः 45° एवं 60° हैं।
पुनः मान लीजिए कि SQ = x m एवं PR = h m (देखिए आकृति 9.9) तो समकोण ∆PQS में,
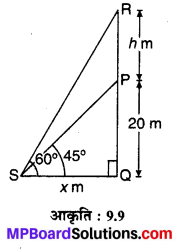
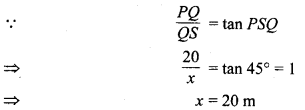
एवं समकोण ∆ROS में,

समीकरण (1) से x = 20 m का मान समीकरण (2) में रखने पर,
⇒ \(\frac { h+20 }{ 20 }\) = √3 ⇒ h + 20 = 20√3
⇒ h = 20√3 – 20 = 20 (√3 – 1) m
अतः, संचार मीनार की अभीष्ट ऊँचाई = 20 (√3 – 1) m है।
प्रश्न 8.
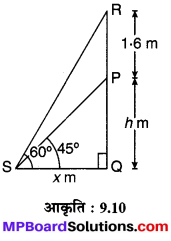
एक पेडस्टल के शिखर पर एक 1.6 m ऊँची मूर्ति लगी है। भूमि के एक बिन्दु से मूर्ति के शिखर का उन्नयन कोण 60° है और उसी बिन्दु से पेडस्टल के शिखर का उन्नयन कोण 45° है। पेडस्टल की ऊँचाई ज्ञात कीजिए।
हल :
मान लीजिए PQ = h m की ऊँचाई का एक पेडस्टल है जिसके ऊपर RP = 1.6 m ऊँची एक मूर्ति लगी है। पेडस्टल के पाद से QS = x m की दूरी पर स्थित बिन्दु S से मूर्ति के शिखर का उन्नयन कोण 60° एवं पेडस्टल के शिखर का उन्नयन कोण 45° है (देखिए आकृति 9.10)
तो समकोण त्रिभुज PQS में,

एवं समकोण त्रिभुज PQS में, \(\frac{R Q}{Q S}=\frac{R P+P Q}{Q S}=\tan R S Q\)
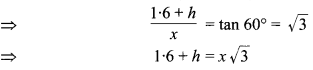
समीकरण (1) से x = h का मान समीकरण (2) में रखने पर,
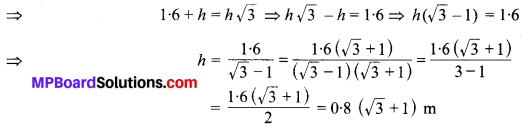
अतः, पेडस्टल की अभीष्ट ऊँचाई = 0.8 (√3 + 1) m है।
![]()
प्रश्न 9.
एक मीनार के पाद बिन्दु से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद बिन्दु से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार 50 m ऊँची हो, तो भवन की ऊँचाई ज्ञात कीजिए।
हल :
मान लीजिए पृथ्वी पर एक मीनार PQ = 50 m ऊँची एवं उसके पाद से QS = x m दूरी पर स्थित एक भवन RS = h m है। मीनार के पाद Q से भवन के शिखर R का उन्नयन कोण ∠ROS = 30° है तथा भवन के पाद S से मीनार के शिखर P का उन्नयन कोण PSQ = 60° है (देखिए आकृति 9.11)। तो समकोण ∆RSQ में,
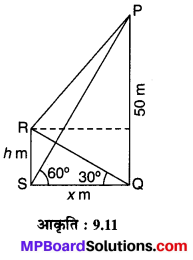
एवं समकोण ∆PQS में,

समीकरण (1) से x = h√3 का मान समीकरण (2) में रखने पर,
h√3 x √3 = 50 ⇒ 3h = 50
⇒ \(h=\frac { 50 }{ 3 }\) = \(16\frac { 2 }{ 3 }\) m
अतः, भवन की अभीष्ट ऊँचाई = \(16\frac { 2 }{ 3 }\) m है।
प्रश्न 10.
एक 80 m चौड़ी सड़क के दोनों ओर आमने-सामने समान लम्बाई वाले दो खम्भे लगे हुए हैं। इन दोनों खम्भों के बीच सड़क के एक बिन्दु से खम्भों के शिखर के उन्नयन कोण क्रमश:
60° और 30° हैं। खम्भों की ऊँचाई और खम्भों से बिन्दु की दूरी ज्ञात कीजिए।
हल :
मान लीजिए दो खम्भे PQ = RS = h m के एक-दूसरे से SQ = 80 m की दूरी पर है। QS के बिन्दु S से ST = x m की दूरी पर बिन्दु T है।
T से R का उन्नयन कोण ∠RTS = 60° एवं P का उन्नयन कोण ∠PTQ = 30° है। यहाँ TQ = SQ – ST = (80 – x)m (देखिए आकृति 9.12)
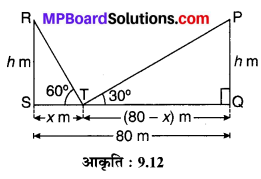
अब समकोण ∆RST में,
\(\frac{R S}{S T}=\tan R T S \Rightarrow \frac{h}{x}=\tan 60^{\circ}=\sqrt{3}\)
h = x √3 …(1)
एवं समकोण ∆PQT में,
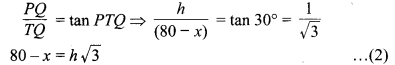
समीकरण (1) से h = x√3 का मान समीकरण (2) में रखने पर,
80 – x = x √3 × √3 = 3x
⇒ 4x = 80 ⇒ x = \(\frac { 80 }{ 4 }\) = 20 m ⇒ ST = 20 m
QT = 80 – x = 80 – 20 = 60 m
x का मान समीकरण (1) में रखने पर,
h = 20√3 m
अतः, प्रत्येक खम्भे की अभीष्ट ऊँचाई = 20√3 m एवं अभीष्ट बिन्दु की स्थिति एक खम्भे से 20 m तथा दूसरे खम्भे से 60 m की दूरी पर है।
प्रश्न 11.
एक नहर के एक तट पर एक टीवी टॉवर ऊर्ध्वाधरतः खड़ा है। टॉवर के ठीक सामने दूसरे तट के एक अन्य बिन्दु से टॉवर के शिखर का उन्नयन कोण 60° है। इसी तट पर इस बिन्दु से 20 m दूर और इस बिन्दु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिन्दु से टॉवर के शिखर का उन्नयन कोण 30° है (देखिए संलग्न आकृति 9.13)। टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए।
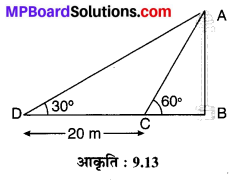
हल :
मान लीजिए कि एक नहर के एक सिरे पर एक मीनार AB = h m दिया है जिसके शिखर A का नहर के दूसरे सिरे से उन्नयन कोण ∠ACB = 60° है। C से DC = 20 m दूरी पर स्थित बिन्दु D से मीनार के शिखर का उन्नयन कोण ∠ADE = 30° है तथा नहर की चौड़ाई CB =x मीटर है तो समकोण ∆ABC में,
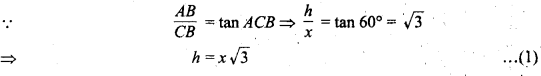
एवं समकोण ∆ABD में,
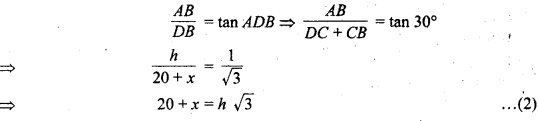
समीकरण (1) से h = x √3 का मान समीकरण (2) में रखने पर,
⇒ 20 + x = x√3 × √3 = 3x
⇒ 2x = 20 ⇒ x = \(\frac { 20 }{ 2 }\) = 10 m
⇒ x = 10 का मान समीकरण (1) में रखने पर,
h = 10√3
अतः, मीनार की अभीष्ट ऊँचाई = 10√3 m एवं नहर की चौड़ाई = 10 m है।
प्रश्न 12.
7 m ऊँचे भवन के शिखर से एक केबल टॉवर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45° है। टॉवर की ऊँचाई ज्ञात कीजिए।
हल :
मान लीजिए केबल टॉवर PQ = h मीटर ऊँचा तथा भवन RS = 7m ऊँचा दिया है। भवन के शिखर से टॉवर के शिखर का उन्नयन कोण ∠PRT = 60° है जहाँ RT क्षैतिज रेखा है जो PQ के बिन्दु T पर मिलती है तथा इस शिखर R से टॉवर के पाद Q का अवनयन कोण ∠TRQ = 45° है। (देखिए आकृति: 9.14)
यहाँ TQ = RS = 7 m एवं PT = (h – 7) m तथा .
RT = SQ = xm तो समकोण ∆RTQ में,
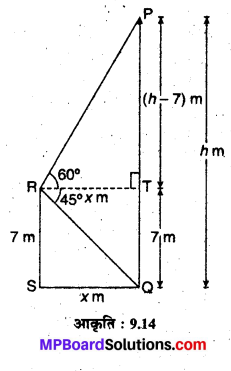
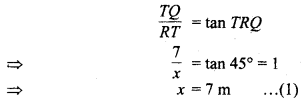
एवं समकोण ∆PRT में,
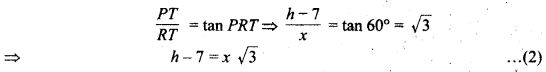
समीकरण (1) से x = 7 समीकरण (2) में रखने पर, .
h – 7 = 7√3
h = 7√3 + 7
= 7(√3 + 1) m
अतः, केबल टॉवर की अभीष्ट ऊँचाई = 7 (√3 + 1) m है।
![]()
प्रश्न 13.
समुद्र तल से 75 m ऊँची लाइट हाउस के शिखर से देखने पर दो समुद्री जहाजों के अवनमन कोण 30° और 45° हैं। यदि लाइट हाउस के एक ही ओर एक जहाज दूसरे जहाज के ठीक
पीछे हो तो जहाजों के बीच की दूरी ज्ञात कीजिए।
हल :
मान लीजिए लाइट हाउस PQ = 75 m ऊँची तथा उसके एक ही ओर दो जहाज R एवं S दिए हैं जिनके अवनमन कोण लाइट हाउस के शिखर P से क्रमश: ∠TPR = 30° एवं ∠TPS = 45° हैं, जहाँ TP एक क्षैतिज रेखा है। (देखिए आकृति 9.15) यहाँ ∠PRQ = ∠TPR = 30° एवं ∠PSQ = ∠TPS = 45° है तथा RS =x m एवं SQ = y m है तो समकोण ∆PQS में,
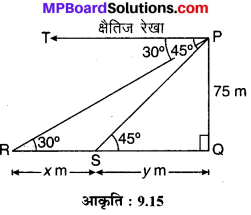
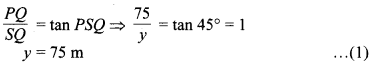
एवं समकोण ∆PQR में,
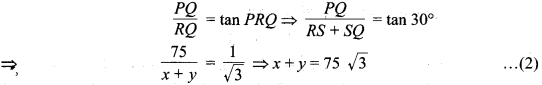
समीकरण (1) से y = 75 m का मान समीकरण (2) में रखने पर,
⇒ x + 75 = 75√5
⇒ x = 75√3 – 75 = 75 (√3 – 1) m
अतः, जहाजों के बीच की अभीष्ट दूरी = 75 (√3 – 1) m है।
प्रश्न 14.
1.2 m लम्बी एक लड़की भूमि से 88.2 m की ऊँचाई पर एक क्षैतिज रेखा में हवा में उड़ रहे गुब्बारे को देखती है। किसी भी क्षण लड़की की आँख से गुब्बारे का उन्नयन कोण 60° है। कुछ समय बाद उन्नयन कोण घटकर 30° हो जाता है (देखिए आकृति: 9.16)। इस अन्तराल के दौरान गुब्बारे द्वारा तय की गयी दूरी ज्ञात कीजिए।
हल :
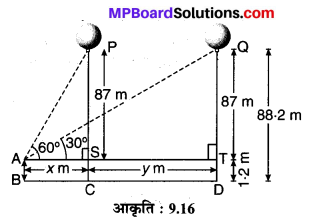
मान लीजिए एक गुब्बारा P पृथ्वी से PC = 88.2 मीटर की ऊँचाई पर एक क्षैतिज रेखा में उड़ रहा है जो कुछ समय बाद वह Q स्थिति में आता है जिसकी ऊँचाई QD = PC = 88.2 m है। एक लड़की AB = 1.2 m की बिन्दु B पर खड़ी है। लड़की के नेत्रों से जाने वाली क्षैतिज रेखा AST है। A से गुब्बारे की प्रथम स्थिति P का उन्नयन कोण ∠PAS = 60° तथा स्थिति Q का उन्नयन कोण ∠QAT = 30° है। यहाँ TD = SC = AB = 1.2 m एवं PS = QT = QD – TD = 88.2 – 1.2 = 87 m तथा AS = x m एवं ST = y m .
तो समकोण ∆PSA में,
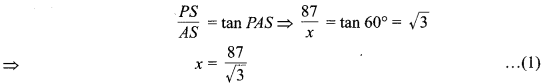
एवं समकोण ∆QTA में,
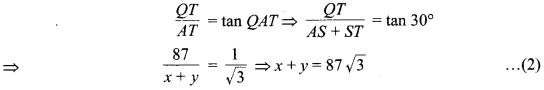
समीकरण (1) से \(x=\frac{87}{\sqrt{3}}\) का मान समीकरण (2) में रखने पर,
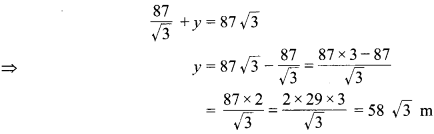
अतः, गुब्बारे द्वारा चली गयी अभीष्ट दूरी = 58√3 m है।
प्रश्न 15.
एक सीधा राजमार्ग एक मीनार के पाद तक जाता है। मीनार के शिखर पर खड़ा एक आदमी एक कार को 30° के अवनमन कोण पर देखता है जो कि मीनार के पाद की ओर एकसमान चाल से जाती है। छः सेकण्ड बाद कार का अवनमन कोण 60° हो गया। इस बिदु से मीनार के पाद तक पहुँचने में कार द्वारा लिया गया समय ज्ञात कीजिए।
हल :
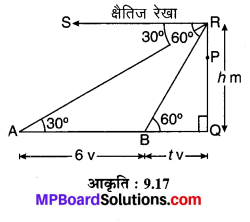
मान लीजिए कि एक आदमी RP किसी मीनार PQ के शिखर P पर खड़ा है तथा स्थिति A पर कार का अवनमन कोण ∠SRA = 30° है तथा कार v m/s की चाल से AB = 6 vm की दूरी तय करते हुए B पर आ जाती है, जहाँ उनका अवनमन कोण ∠SRB = 60° हो जाता है। इस बिन्दु से मीनार के पाद तक जाने में 1 सेकण्ड में BQ = tv m दूरी तय करती है, तो
∠RAQ = ∠SRA = 30°
एवं ∠RBQ = ∠SRB = 60°
क्योंकि उन्नयन कोण अवनमन कोण के बराबर होते हैं। यदि आदमी सहित मीनार की ऊँचाई RQ = h m हो तो समकोण ∆RQB में,
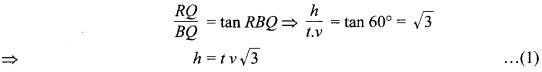
एवं समकोण ∆RQA में,
![]()
![]()
समीकरण (1) से h का मान समीकरण (2) में रखने पर,
tv√3 x √3 = 6v + tv
3tv = 6v + tv ⇒ 2t = 6 ⇒ t = \(\frac { 6 }{ 2 }\) = 3
अतः, कार द्वारा लिया गया अभीष्ट समय = 3 सेकण्ड है।
प्रश्न 16.
मीनार के आधार से एक सरल रेखा में 4m और 9 m की दूरी पर स्थित दो बिन्दुओं से मीनार के शिखर के उन्नयन कोण पूरक कोण हैं। सिद्ध कीजिए कि मीनार की ऊँचाई 6 m है।
हल :
मान लीजिए एक मीनार PQ = h m ऊँची है जिसके पाद से AQ = 4 m एवं BQ = 9 m की दूरी पर दो बिन्दु क्रमशः A और B स्थित हैं, जहाँ पर मीनार के शिखर के उन्नयन कोण क्रमशः ∠PAQ = θ एवं ∠PBQ = (90° – θ) हैं, क्योंकि दोनों कोण पूरक कोण हैं।
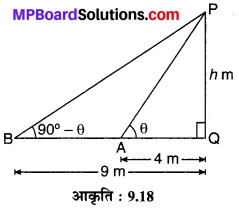
अब समकोण ∆PQA में,
![]()
एवं समकोण ∆PQB में,

अतः, मीनार की ऊँचाई 6 m है।
इति सिद्धम्