MP Board Class 10th Maths Solutions Chapter 7 निर्देशांक ज्यामिति Ex 7.4

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 7 निर्देशांक ज्यामिति Ex 7.4 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 7 निर्देशांक ज्यामिति Ex 7.4

[ज्ञातव्य : यह प्रश्नावली परीक्षा की दृष्टि से नहीं है।]

प्रश्न 1.
बिन्दुओं A (2, – 2) और B (3, 7) को जोड़ने वाले रेखाखण्ड 2x + y – 4 = 0 को जिस अनुपात में विभाजित करती है उसे ज्ञात कीजिए।
हल :
मान लीजिए कि दिए हुए रेखाखण्ड और दी गई रेखा बिन्दु P (x, y) पर परस्पर प्रतिच्छेद करती है तो ∆PAB का क्षेत्रफल शून्य होगा क्योंकि ये सरेख हैं।
⇒ \(\frac { 1 }{ 2 }\) [x (-2 – 7) + 2 (7 – y) + 3 (y + 2)] = 0
⇒ – 9x + 14 – 2y + 3y + 6 = 0
⇒ 9x – y – 20 = 0 …(1)
⇒ 2x + y – 4 = 0 (दिया है) …(2)
⇒ 11x = 24
⇒ x = \(\frac { 24 }{ 11 }\)
मान लीजिए बिन्दु P (x, y), A (2, – 2) और B (3, 7) से बने रेखाखण्ड AB को m₁ एवं m₂ के अनुपात में विभाजित करता है।

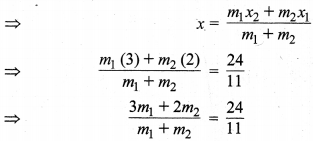
⇒ 33m₁ + 22m₂ = 24m₁ + 24m₂
⇒ 33m₁ – 24m₁ = 24m₂ – 22m₂
⇒ 9m₁ = 2m₂
⇒ \(\frac{m_{1}}{m_{2}}=\frac{2}{9}\)
⇒ m₁ : m₂ = 2 : 9
अतः अभीष्ट अनुपात 2 : 9 है।

प्रश्न 2.
x और में एक सम्बन्ध ज्ञात कीजिए यदि बिन्दु (x, y), (1, 2) और (7, 0) सरेखी हैं।
हल :
चूँकि बिन्दु (x, y), (1, 2) और (7, 0) सरेख हैं, इसलिए उनसे निर्मित त्रिभुज का क्षेत्रफल = 0 है
⇒ \(\frac { 1 }{ 2 }\) [x (2 – 0) + 1 (0 – y) + 7 (y – 2) = 0
⇒ x (2) + 1 (-y) + 7 (y – 2) = 0
⇒ 2x – y + 7y – 14 = 0
⇒ 2x + 6y – 14 = 0
⇒ x + 3y = 7
अतः x एवं का अभीष्ट सम्बन्ध x + 3y = 7 है।

प्रश्न 3.
बिन्दुओं (6,-6), (3, – 7) और (3, 3) से होकर जाने वाले वृत्त का केन्द्र ज्ञात कीजिए।
हल :
मान लीजिए दिए हुए बिन्दुओं A (6, -6), B (3, – 7) और C (3, 3) से होकर जाने वाले वृत्त का केन्द्र O (x, y) है तो OA = OB = OC वृत्त की त्रिज्याएँ हैं।

⇒ (x – 6)² + (y + 6)² = (x – 3)² + (y + 7)² = (x – 3)² + (y – 3)² (दोनों ओर वर्ग करने पर)
⇒ (x – 6)² + (y + 6)² = (x – 3)² + (y + 7)² (OA = OB से)
⇒ x² – 12x + 36 + y² + 12y + 36 = x² – 6x + 9 + y² + 14y + 49
⇒ – 12x + 6x + 12y – 14y + 72 – 58 = 0
⇒ – 6x – 2y + 14 = 0
⇒ 3x + y = 7 ….(1)
⇒ (x – 3)² + (y + 7)² = (x – 3)² + (y – 3)² (OB = OC से)
⇒ x² – 6x + 9 + y² + 14y + 49 = x² – 6x + 9 + y² – 6y + 9
⇒ -6x + 6x + 14y + 6y = 18 – 58
⇒ 20y = – 40
⇒ y = \(\frac { -40 }{ 20 }\) =- 2 …..(2)
समीकरण (2) से y = – 2 का मान समीकरण (1) में रखने पर,
⇒ 3x – 2 = 7
⇒ 3x = 7 + 2
⇒ 3x = 9
⇒ x = \(\frac { 9 }{ 3 }\) = 3
अतः वृत्त के केन्द्र के अभीष्ट निर्देशांक (3, – 2) हैं।

प्रश्न 4.
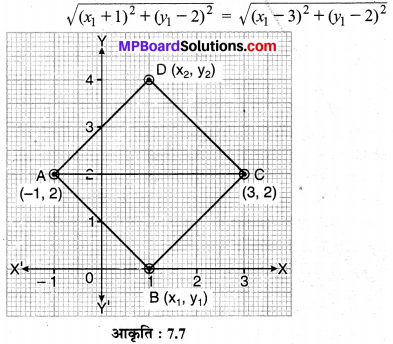
किसी वर्ग के दो सम्मुख शीर्ष (-1, 2) और (3, 2) हैं। वर्ग के अन्य दोनों शीर्ष ज्ञात कीजिए।
हल :
वर्ग ABCD में दो सम्मुख शीर्ष A (-1, 2) एवं C (3, 2) दिए हैं। मान लीजिए B (x₁, y₁) एवं D (x₂, y₂) दो अन्य शीर्ष हैं।
AB = BC (वर्ग की भुजाएँ)

⇒ (x₁ + 1)² + (y₁ – 2)² = (x₁ – 3)² + (y₁ – 2)² (दोनों ओर वर्ग करने पर)
⇒ (x₁ + 1)² = (x₁ – 3)²
⇒ x₁² + 2x₁ + 1 = x₁² – 6x₁ + 9
⇒ 2x₁ + 6x₁ = 9 – 1
⇒ 8x₁ = 8
⇒ x₁ = \(\frac { 8 }{ 8 }\) = 1 ….(1)
∵ AB² + BC² = AC² (समकोण ∆ABC में पाइथागोरस प्रमेय से)
⇒ (x₁ + 1)² + (y₁ – 2)² + (x₁ – 3)² + (y₁ – 2)² = (3 + 1)² + (2 – 2)²
⇒ x₁² + 2x₁ + 1 + y₁² – 4y₁ + 4 + x₁² – 6x₁ + 9 + y₁² – 4y₁ + 4 = 16 – 0
⇒ 2x₁² + 2y₁² – 4x₁ – 8y₁ = 16 – 18 = -2
⇒ x₁² + y₁² – 2x₁ – 4y₁ + 1 = 0 …(2)
⇒ x₁ = 1 का मान समीकरण (1) से समीकरण (2) में रखने पर,
⇒ (1)² + (y₁)² – 2 (1) – 4y₁ + 1 = 0
⇒ y₁² – 4y₁ = 0
⇒ y₁ (y₁ – 4) = 0
या तो y₁ = 0 अथवा y₁ – 4 = 0
⇒ y₁ = 4
B के निर्देशांक (1, 0) अथवा (1, 4) हैं।
AD = DC (वर्ग की भुजाएँ हैं)

⇒ (x₂ + 1)² + (y₂ – 2)² = (x₂ – 3)² + (y₂ – 2)² (दोनों ओर वर्ग करने पर)
⇒ (x₂ + 1)² = (x₂ – 3)²
⇒ x₂² + 2x₂ + 1 = x₂² – 6x₂ + 9
⇒ 8x₂ = 8
⇒ x₂ = \(\frac { 8 }{ 8 }\) = 1 . …(3)
AD² + CD² = AC² (समकोण ∆ADC में पाइथागोरस प्रमेय से)
⇒ (x₂ + 1)² + (y₂ – 2)² + (x₂ – 3)² + (y₂ – 2)² = (3 + 1)² + (2 – 2)²
⇒ x₂² + 2x₂ + 1 + y₂² – 4y₂ + 4 + x₂² – 6x₂ + 9 + y₂² – 4y₂ + 4 = 16 + 0
⇒ 2x₂² + 2y₂² – 4x₂ – 8y₂ = 16 – 18 = -2
⇒ x₂² + y₂² – 2x₂ – 4y₂ + 1 = 0 ….(4)
x₂ = 1 का मान समीकरण (3) से समीकरण (4) में रखने पर,
⇒ (1)² + y₂² – 2 (1) – 4y₂ + 1 = 0
⇒ 1 + y₂² – 2 – 4y₂ + 1 = 0
⇒ y₂² – 4y₂ = 0
⇒ y₂ (y₂ – 4) = 0
या तो y₂ = 0 अथवा y₂ – 4 = 0
⇒ y₂ = 4
D के निर्देशांक (1, 0) अथवा (1, 4)
अतः अभीष्ट शीर्षों के निर्देशांक क्रमशः (1, 0) एवं (1, 4) हैं।

प्रश्न 5.
कृष्णा नगर के एक सेकेंडरी स्कूल के कक्षा X के विद्यार्थियों को उनके बागवानी क्रियाकलाप के लिए एक आयताकार भू-खण्ड दिया गया है। गुलमोहर की पौध (Sapling) को परस्पर 1 m की दूरी पर इस भू-खण्ड की परिसीमा (boundary) पर लगाया जाता है। इस भू-खण्ड के अन्दर एक त्रिभुजाकार घास लगा हुआ लॉन (lawn) है, जैसा कि संलग्न आकृति 7.8 में दर्शाया गया है। विद्यार्थियों , को भू-खण्ड के शेष भाग में है फूलों के पौधे के बीज बोने हैं।

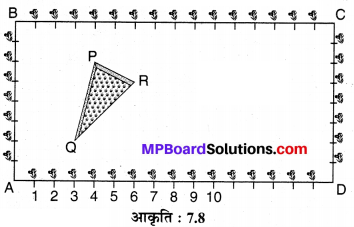
(i) A को मूलबिन्दु मानते हए, त्रिभुज के शीषों के निर्देशांक ज्ञात कीजिए।
(ii) यदि मूल बिन्दु C हो, तो ∆PQR के शीर्षों के निर्देशांक क्या होंगे?
साथ ही उपरोक्त दोनों स्थितियों में त्रिभुजों के क्षेत्रफल ज्ञात कीजिए। आप क्या देखते हैं?
हल :
(i) A को मूलबिन्दु लेकर लेखाचित्र के अनुसार अभीष्ट निर्देशांक P (4, 6), Q (3, 2), R (6,5) हैं। AD = X-अक्ष एवं AB = Y-अक्ष पर मानने पर।
(ii) C को मूलबिन्दु लेकर लेखाचित्र के अनुसार,
अभीष्ट निर्देशांक P (12, 2), Q (13, 6), R (10, 3) हैं। CB = X-अक्ष एवं CD = Y-अक्ष पर मानने पर।
अब प्रथम स्थिति में :
ar (PQR) = \(\frac { 1 }{ 2 }\)[4(2 – 5) + 3 (5 – 6) + 6 (6 – 2)]
ar (PQR) = \(\frac { 1 }{ 2 }\)[4(-3) + 3 (-1) + 6 (4]
= \(\frac { 1 }{ 2 }\) [-12 – 3 + 24]
= \(\frac { 1 }{ 2 }\)[-15 + 24]
= \(\frac { 9 }{ 2 }\) m²
एवं द्वितीय स्थिति में :
ar (PQR) = \(\frac { 1 }{ 2 }\) [12 (6 – 3) + 13 (3 – 2) + 10 (2 – 6)]
= \(\frac { 1 }{ 2 }\) [12 (3) + 13 (1) + 10 (-4)]
= \(\frac { 1 }{ 2 }\) [36 + 13 – 40]
= \(\frac { 1 }{ 2 }\) [49 – 40]
= \(\frac { 9 }{ 2 }\) m²
अतः प्रत्येक स्थिति में APQR का क्षेत्रफल = \(\frac { 9 }{ 2 }\) m² है।

प्रश्न 6.
एक त्रिभुज ABC के शीर्ष A (4, 6), B (1, 5) और C (7, 2) हैं। भुजाओं AB और AC को क्रमश: D और E पर प्रतिच्छेद करते हुए एक रेखा इस प्रकार खींची गयी है कि \(\frac{A D}{A B}=\frac{A E}{A C}=\frac{1}{4}\) है। ∆ADE का क्षेत्रफल परिकलित कीजिए और इसकी तुलना ∆ABC के क्षेत्रफल से कीजिए।
हल :

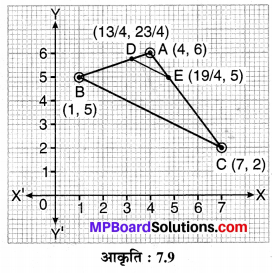
∆ADE और ∆ABC में,

बिन्दु D, AB रेखाखण्ड को 1 : 3 के अनुपात में विभाजित करता है क्योंकि AD : AB = 1 : 4
AD : DB = 1 : 3. इसलिए D के निर्देशांक


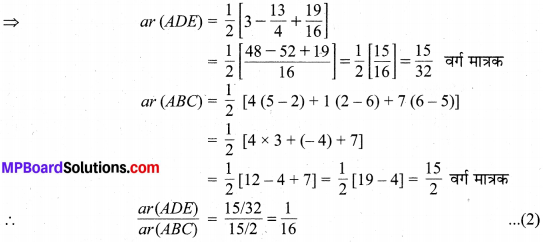
अत: ∆ADE का अभीष्ट क्षेत्रफल = \(\frac { 15 }{ 32 }\) त्रक एवं ∆ADE और ∆ABC के क्षेत्रफलों का अभीष्ट अनुपात 1 : 16 है।

प्रश्न 7.
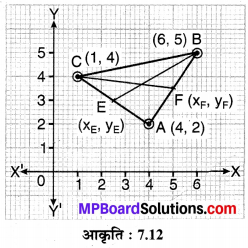
मान लीजिए A (4, 2), B (6, 5) और C (1, 4) एक ∆ABC के शीर्ष हैं।
(i) A से जाने वाली माध्यिका BD के बिन्दु पर मिलती है। बिन्दु के निर्देशांक ज्ञात कीजिए।
(ii) AD पर स्थित ऐसे बिन्दु P के निर्देशांक ज्ञात कीजिए कि AP : PD = 2 : 1 हो।
(iii) माध्यिकाओं BE और CF पर ऐसे बिन्दुओं Q और R के निर्देशांक ज्ञात कीजिए कि BQ : QE = 2 : 1 हो और CR : RF = 2 : 1 हो।
(iv) आप क्या देखते हैं?
(v) यदि A (x₁, y₁), B (x₂, y₂) और C (x₃, y₃) त्रिभुज ABC के शीर्ष हैं, तो इस त्रिभुज के केन्द्रक के निर्देशांक ज्ञात कीजिए।
हल :
(i) चूँकि D, BC का मध्य-बिन्दु है। इसलिए D के निर्देशांक


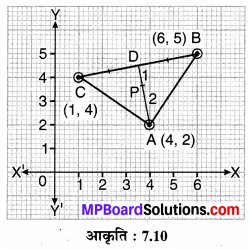
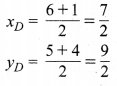
अतः बिन्दु D के अभीष्ट निर्देशांक \(D\left(\frac{7}{2}, \frac{9}{2}\right)\) हैं।

(ii) चूँकि P, AD रेखाखण्ड (माध्यिका) को 2 : 1 के अनुपात में विभाजित करता है।


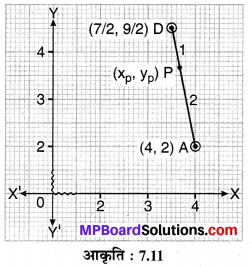
अत: P के अभीष्ट निर्देशांक \(P\left(\frac{11}{3}, \frac{11}{3}\right)\) है।

(iii) बिन्दु E, AC रेखाखण्ड का मध्य-बिन्दु है। इसलिए E के निर्देशांक


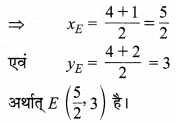
तथा बिन्दु F, रेखाखण्ड AB का मध्य-बिन्दु है। इसलिए बिन्दु F के निर्देशांक

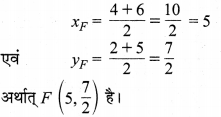
चूँकि बिन्दु Q रेखाखण्ड (माध्यिका) BE को 2 : 1 के अनुपात में विभाजित करता है। इसलिए Q के निर्देशांक


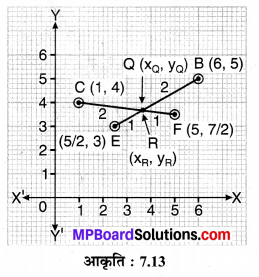
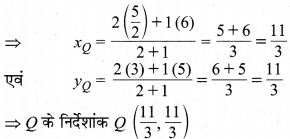
और बिन्दु R रेखाखण्ड (माध्यिका) CF को 2 : 1 के अनुपात में विभाजित करता है। इसलिए R के निर्देशांक

अत: बिन्दु Q एवं R के अभीष्ट निर्देशांक क्रमशः \(Q\left(\frac{11}{3}, \frac{11}{3}\right)\) एवं \(R\left(\frac{11}{3}, \frac{11}{3}\right)\) हैं।

(iv) त्रिभुज की तीनों माध्यिकाओं को 2 : 1 के अनुपात में विभाजित करने वाले सभी बिन्दु P, Q एवं R समानुपाती हैं अर्थात् एक ही हैं जिसे त्रिभुज का केन्द्रक कहते हैं तथा इसे प्रायः G से प्रदर्शित करते हैं।

(v) त्रिभुज का केन्द्रक उसकी माध्यिकाओं का संगामी बिन्दु होता है जो प्रत्येक माध्यिका को 2 : 1 के अनुपात में विभाजित करता हैं।

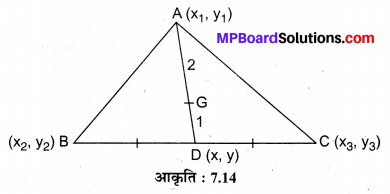
चूँकि बिन्दु D (x,y) मान लीजिए है जो बिन्दुओं B (x₂, y₂) और C (x₃, y₃) को मिलाने वाले रेखाखण्ड का मध्य बिन्दु है।

अत: केन्द्रक G के अभीष्ट निर्देशांक G \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\) हैं।

प्रश्न 8.
बिन्दुओं A (-1, – 1), B (-1, 4), C (5, 4) और D (5, – 1) से एक आयत ABCD बनता है। P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिन्द हैं। क्या चतुर्भुज PQRS एक वर्ग है? क्या यह एक आयत है? क्या यह एक समचतुर्भुज है? सकारण उत्तर दीजिए।
हल :

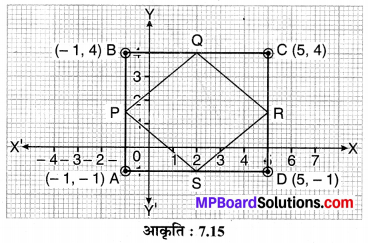
चूँकि P, A (-1, – 1) और B (-1, 4) से बने रेखाखण्ड AB का मध्य-बिन्दु है।

चूँकि Q, B (-1, 4) और C (5, 4) से बने रेखाखण्ड BC का मध्य-बिन्दु है।

चूँकि R, C (5, 4) और D (5, – 1) से बने रेखाखण्ड CD का मध्य-बिन्दु है।

चूँकि S, D (5, – 1) और A (-1,- 1) से बने रेखाखण्ड DA का मध्य-बिन्दु है।


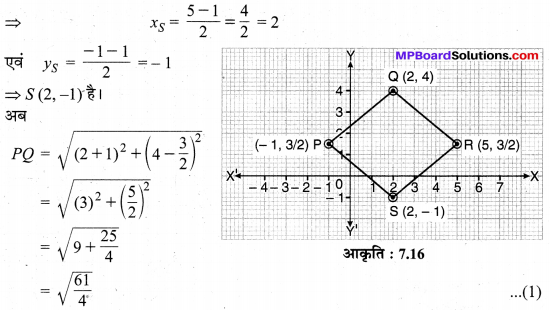
लेकिन विकर्ण PR ≠ QS अर्थात् 6 ≠ 5
अतः अभीष्ट ₹PQRS एक समचतुर्भुज है।