In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.2 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.2
प्रश्न 1.
6 cm त्रिज्या वाले एक वृत्त के एक त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 60° है। (2019)
हल :
ज्ञात है : r = 6 cm एवं θ° = 60°
चूँकि त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\theta^{\circ}}{360^{\circ}} \times \pi r^{2}\)
त्रिज्यखण्ड का क्षेत्रफल = \(\frac{60}{360} \times \frac{22}{7} \times(6)^{2}\)
= \(\frac{132}{7} \mathrm{cm}^{2}\)
अतः अभीष्ट क्षेत्रफल = \(\frac{132}{7} \mathrm{cm}^{2}\)
प्रश्न 2.
एक वृत्त के चतुर्थांश (quadrant) का क्षेत्रफल ज्ञात कीजिए जिसकी परिधि 22 cm है।
हल :
चूंकि परिधि = 2πr
2 x \(\frac { 22 }{ 7 }\) x r = 22
\(r=\frac{22 \times 7}{2 \times 22}=\frac{7}{2} \mathrm{cm}\)
चूँकि चतुर्थांश का क्षेत्रफल = \(\frac{1}{4} \pi r^{2}\)
चतुर्थाश का क्षेत्रफल = \(\frac{1}{4} \times \frac{22}{7} \times\left(\frac{7}{2} \times \frac{7}{2}\right)\)
= \(\frac{77}{8} \mathrm{cm}^{2}\)
अतः चतुर्थांश का अभीष्ट क्षेत्रफल = \(\frac{77}{8} \mathrm{cm}^{2}\)
प्रश्न 3.
एक घड़ी की मिनट की सुई जिसकी लम्बाई 14 cm है। इस सुई द्वारा 5 मिनट में रचित क्षेत्रफल ज्ञात कीजिए।
हल :
चूँकि मिनट सुई 1 घण्टे में (60 मिनट में) वृत्त का एक चक्कर लगाती है।
इसलिए 5 मिनट में \(\frac{5}{60}=\frac{1}{12}\) वृत्त को रचेगी।
इस वृत्त की त्रिज्या r = सुई की लम्बाई = 14 cm
वृत्त के अंश का क्षेत्रफल
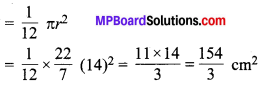
अतः अभीष्ट क्षेत्रफल = \(\frac{154}{3} \mathrm{cm}^{2}\) है।
प्रश्न 4.
10 cm त्रिज्या वाले एक वृत्त की कोई जीवा केन्द्र पर एक समकोण अन्तरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिए :
(i) संगत लघु वृत्तखण्ड।
(ii) संगत दीर्घ त्रिज्यखण्ड। (π = 3.14 का प्रयोग कीजिए)
हल :
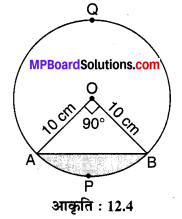
दिया है : r = 10 cm एवं θ = 90°
(i) चूँकि लघु त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\theta}{360} \pi r^{2}\)
ar (OAPB) = \(\frac { 90 }{ 360 }\) x 3.14 x (10)²
= \(\frac { 1 }{ 4 }\) x 3.14 x 100
ar (OAPB) = 78.5 cm²
ar (∆OAB) = \(\frac { 1 }{ 2 }\) OA x OB
ar (OAB) = \(\frac { 1 }{ 2 }\) x 10 x 10 = 50 cm² …(2)
चूँकि संगत लघु वृत्तखण्ड का क्षेत्रफल
ar (APB) = ar (OAPB) – ar (OAB)
= 78.5 – 50 = 28.5 cm² [समीकरण (1) एवं (2) से]
अतः संगत लघु वृत्त खण्ड का अभीष्ट क्षेत्रफल = 28.5 cm² है।
(ii) चूँकि संगत दीर्घ त्रिज्यखण्ड का क्षेत्रफल = \(\frac{360-\theta}{360} \pi r^{2}\)
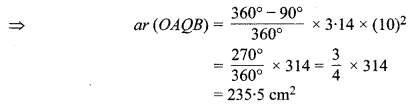
अतः संगत दीर्घ त्रिज्यखण्ड का अभीष्ट क्षेत्रफल = 235.5 cm² है।
![]()
प्रश्न 5.
त्रिज्या 21 cm वाले वृत्त का एक चाप केन्द्र पर 60° का कोण अन्तरित करता है। ज्ञात कीजिए :
(i) चाप की लम्बाई (2019)
(ii) चाप द्वारा बनाए गए त्रिज्यखण्ड का क्षेत्रफल (2019)
(iii) संगत जीवा द्वारा बनाए गए वृत्तखण्ड का क्षेत्रफल।
हल :
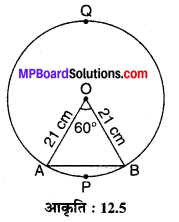
(i) चूंकि चाप की लम्बाई = \(\frac{\theta^{\circ}}{360^{\circ}} \times 2 \pi r\)
चाप की लम्बाई = \(\frac{60^{\circ}}{360^{\circ}} \times 2 \times \frac{22}{7} \times 21\)
चाप (APB) = \(\frac { 1 }{ 6 }\) x 22 x 6 = 22 cm
अतः चाप की अभीष्ट लम्बाई = 22 cm
(ii) चूँकि त्रिज्यखण्ड का क्षेत्रफल = \(\frac { 1 }{ 2 }\)
ar (OAPB) = \(\frac { 1 }{ 2 }\)
= \(\frac { 1 }{ 6 }\) x 22 x 3 x 21 = 231 cm²
अतः चाप द्वारा बनाए गए त्रिज्यखण्ड का अभीष्ट क्षेत्रफल = 231 cm² है।
(iii) चूँकि ∆OAB में ∠AOB = 60° एवं ∠OAB = ∠OBA
तथा ∠OAB + ∠OBA = 180° – 60° = 120°
∠OAB = ∠OBA = \(\frac { 120 }{ 2 }\) = 60°
∆OAB एक समबाहु त्रिभुज है जिसकी भुजा = 21 cm
चूँकि समबाहु ∆ का क्षेत्रफल = \(\frac{\sqrt{3}}{4}\) (भुजा)²
ar(OAB) = \(\frac{\sqrt{3}}{4}(21)^{2}=\frac{441 \sqrt{3}}{4} \mathrm{cm}^{2}\)
और चूँकि वृत्तखण्ड का क्षेत्रफल = संगत त्रिज्यखण्ड का क्षेत्रफल – संगत त्रिभुज का क्षेत्रफल
ar (APB) = ar (OAPB) – ar (OAB)
= \(\left(231-\frac{441 \sqrt{3}}{4}\right) \mathrm{cm}^{2}\)
अतः संगत जीवा द्वारा बनाए गए वृत्तखण्ड का अभीष्ट क्षेत्रफल = \(\left(231-\frac{441 \sqrt{3}}{4}\right) \mathrm{cm}^{2}\) है।
प्रश्न 6.
15 cm त्रिज्या वाले एक वृत्त की कोई जीवा केन्द्र पर 60° का कोण अन्तरित करती है। संगत लघु और दीर्घ वृत्तखण्डों के क्षेत्रफल ज्ञात कीजिए।
(π = 3.14 और √3 = 1.73 का प्रयोग कीजिए।)
हल :
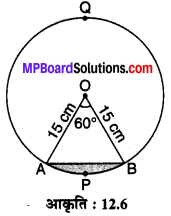
ज्ञात है : वृत्त की त्रिज्या OA = OB = 15 cm
एवं ∠AOB = 60°
∠OAB + ∠OBA = 180° – 60°
= 120° …(1)
और ∠OAB = ∠OBA …(2) [∵ OA = OB]
∠OAB = ∠OBA
= \(\frac { 1 }{ 2 }\) x 120° = 60°[समीकरण (1) एवं (2) से]
∆OAB एक समबाहु त्रिभुज है जिसकी प्रत्येक भुजा 15 cm
चूँकि त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\theta}{360^{\circ}} \times \pi r^{2}\)
ar (OAPB) = \(\frac{60^{\circ}}{360^{\circ}}\) x 3.14 x 15 x 15
= \(\frac { 1 }{ 6 }\) x 3.14 x 15 x 15
= 1.57 x 75
ar (OAPB) = 117.75 cm² …(3)
चूँकि समबाहु त्रिभुज का क्षेत्रफल = \(\frac{\sqrt{3}}{4}\) (भुजा)²
ar (OAB) = \(\frac{\sqrt{3}}{4} \times 15 \times 15=\frac{225 \sqrt{3}}{4}\)
ar (OAB) = \(\frac{225 \times 1 \cdot 73}{4}\) = 97.31 cm² [लगभग] …(4)
चूँकि लघु वृत्तखण्ड APB का क्षेत्रफल = त्रिज्यखण्ड OAPB का क्षेत्रफल – ∆OAB का क्षेत्रफल
ar (APB) = ar (OAPB) – ar (OAB)
ar (APB) = 117.75 – 97.31
= 20.44 cm² …(5)
[समीकरण (3) एवं (4) से मान रखने पर ]
चूँकि वृत्त का क्षेत्रफल = πr²
= 3.14 x 15 x 15
= 706.5 cm² …(6)
चूँकि दीर्घ वृत्तखण्ड का क्षेत्रफल = वृत्त का क्षेत्रफल – लघु वृत्तखण्ड का क्षेत्रफल
ar (AQB) = 706.5 – 20.44
= 686.06 cm² (लगभग)
अतः लघु वृत्तखण्ड का अभीष्ट क्षेत्रफल = 20.44 cm² (लगभग) एवं दीर्घ वृत्तखण्ड का अभीष्ट क्षेत्रफल = 686.06 cm² (लगभग) है।
प्रश्न 7.
त्रिज्या 12 cm वाले एक वृत्त की कोई जीवा केन्द्र पर 120° का कोण अन्तरित करती है। संगत वृत्तखण्ड का क्षेत्रफल ज्ञात कीजिए।
(π = 3.14 और √3 = 1.73 का प्रयोग कीजिए।)
हल :
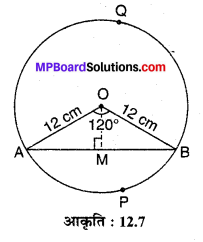
ज्ञात है : केन्द्र O वाला वृत्त जिसकी त्रिज्या 12 cm है तथा एक जीवा AB केन्द्र O पर ∠AOB = 120° का कोण बनाती है।
O से OM ⊥ AB खींचिए जो AB को M पर प्रतिच्छेद करती है।
चूँकि समद्विबाहु त्रिभुज OAB में OM शीर्ष लम्ब है।
इसलिए यह ∠AOB = 120° को समद्विभाजित करेगी
अर्थात्
∠AOM = ∠BON = \(\frac { 120 }{ 2 }\) = 60°
एवं AM = BM = \(\frac { 1 }{ 2 }\) AB.
अब समकोण ∆OMA में,
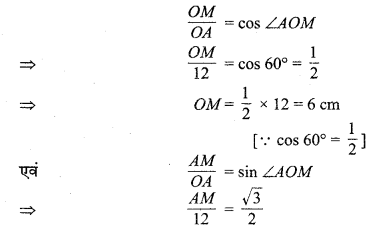
AM = 6 √3 = 6 x 1.73 = 10.38 cm
[∵ sin 60° = \(\frac{\sqrt{3}}{2}\) ]
AB = 2 AM = 2 x 10.38 = 20.76 cm
त्रिभुज OAB का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x AB x OM
ar (OAB) = \(\frac { 1 }{ 2 }\) x 20.76 x 6 = 62.28 cm² …(1)
चूँकि त्रिज्यखण्ड OAPB का क्षेत्रफल = \(\frac { 120 }{ 360 }\) x 3.14 x (12)²
ar (OAPB) = 3.14 x 48 = 150.72 cm² ….(2)
चूँकि वृत्तखण्ड APB = ar (OAPB) – ar (OAB)
ar (APB) = 150.72 – 62.28
[समीकरण (1) एवं (2) से मान रखने पर]
ar (APB) = 88.44 cm²
अतः संगत वृत्तखण्ड का अभीष्ट क्षेत्रफल = 88.44 cm² है।
प्रश्न 8.
15 m भुजा वाले एक वर्गाकार घास के मैदान के एक कोने पर लगे खूटे से घोड़े को 5 m लम्बी रस्सी से बाँध दिया गया है (देखिए संलग्न आकृति 12.8) ज्ञात कीजिए :
(i) मैदान के उस भाग का क्षेत्रफल जहाँ घोड़ा घास चर सकता है।
(ii) चरे जा सकने वाले क्षेत्रफल में वृद्धि यदि घोड़े को 5 m रस्सी के स्थान पर 10 m लम्बी रस्सी से बाँध दिया जाय। (π = 3.14 का प्रयोग कीजिए।)
हल :
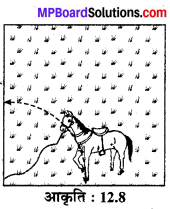
(i) घोड़े द्वारा घास चरे जा सकने वाला मैदान एक वृत्त का चतुर्थांश होगा जिसकी त्रिज्या 5 m है।
मैदान का क्षेत्रफल = \(\frac { 1 }{ 4 }\) x 3.14 x (5)²
\(A_{1}=\frac{78 \cdot 50}{4}\)
= 19.625 m²
अतः घास के मैदान का अभीष्ट क्षेत्रफल = 19.625 m² है।
(ii) अब घोड़े द्वारा चरे जा सकने वाले घास का मैदान 10 m त्रिज्या के वृत्त का चतुर्थांश होगा
मैदान का क्षेत्रफल = \(\frac { 1 }{ 4 }\) x 3.14 x (10)²
A2 = 78.5 m²
घास के मैदान में वृद्धि = A2 – A1 = 78.5 – 19.625
= 58.875 m²
अतः घास के मैदान में अभीष्ट वृद्धि = 58.875 m² है।
![]()
प्रश्न 9.
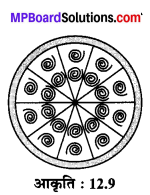
एक वृत्ताकार बूच (brough) को चाँदी के तार से बनाया जाता है, जिसका व्यास 35 mm है। तार को वृत्त के 5 व्यासों को बनाने में प्रयुक्त किया गया है जो उसे 10 बराबर त्रिज्यखण्डों में विभाजित करता है जैसा कि संलग्न आकृति 12.9 में दर्शाया गया है। तो ज्ञात कीजिए :
(i) कुल वांछित चाँदी के तार की लम्बाई।
(ii) बूच के प्रत्येक त्रिज्यखण्ड का क्षेत्रफल।
हल :
(i) चाँदी के तार से वृत्त की परिमाप एवं पाँच व्यास बनाने हैं। व्यास = 35 mm दिया है।
वृत्त की परिमाप (परिधि) = πd = \(\frac { 22 }{ 7 }\) x 35 = 110 mm
पाँच व्यासों की लम्बाई = 5 x d = 5 x 35 = 175 mm
तार की कुल लम्बाई = 110 mm + 175 mm = 285 mm
अतः वांछित चाँदी के तार की अभीष्ट लम्बाई = 285 mm है।
(ii) पाँच व्यासों द्वारा वृत्त 10 बराबर त्रिज्यखण्डों में विभाजित हो रहा है।
इसलिए प्रत्येक त्रिज्यखण्ड का क्षेत्रफल = \(\frac{1}{10} \times \frac{22}{7} \times \frac{35}{2} \times \frac{35}{2}\)
= \(\frac{11 \times 35}{4}=\frac{385}{4}\)
अतः प्रत्येक त्रिज्यखण्ड का अभीष्ट क्षेत्रफल = \(\frac{385}{4} \mathrm{mm}^{2}\) है।
प्रश्न 10.
एक छतरी में आठ ताने हैं, जो बराबर दूरी पर लगे हुए हैं। (देखिए संलग्न आकृति 12.10)। छतरी को 45 cm त्रिज्या वाला एक सपाट वृत्त मानते हुए इसकी दो क्रमांगत तानों के बीच का क्षेत्रफल ज्ञात कीजिए।
हल :

बराबर दूरी पर लगी आठ तानें वृत्त को आठ बराबर त्रिज्यखण्डों में विभक्त करती हैं जिसकी त्रिज्या 45 cm दी है।
प्रत्येक त्रिज्यखण्ड का क्षेत्रफल
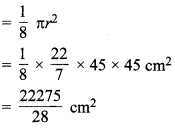
अतः दो तानों के बीच अभीष्ट क्षेत्रफल = \(\frac{22275}{28} \mathrm{cm}^{2}\) है।
प्रश्न 11.
किसी कार के दो वाइपर (Wiper) हैं, परस्पर कभी भी अच्छादित नहीं होते हैं। प्रत्येक वाइपर की पत्ती की लम्बाई 25 cm है और 115° के कोण तक घूमकर सफाई कर सकता है। पत्तियों
की प्रत्येक बुहार के साथ जितना क्षेत्रफल साफ हो जाता है, वह ज्ञात कीजिए।
हल :
प्रत्येक वाइपर 25 cm की त्रिज्या वाले उस त्रिज्यखण्ड का क्षेत्रफल साफ करता है जिसकी त्रिज्याओं के बीच कोण θ = 115° है।
दोनो वाइपरों द्वारा कुल साफ किया गया क्षेत्रफल (एक बार में)

अतः दोनों वाइपरों द्वारा प्रत्येक बुहार में साफ किया गया अभीष्ट क्षेत्रफल = \(\frac{158125}{126}\) है।
प्रश्न 12.
जहाजों को समुद्र में जल स्तर के नीचे स्थित चट्टानों को चेतावनी देने के लिए, एक लाइट हाउस (Light house) 80° कोण वाले एक त्रिज्यखण्ड में 16.5 km की दूरी तक लाल रंग का प्रकाश फैलाता है। समुद्र के उस भाग का क्षेत्रफल ज्ञात कीजिए जिससे जहाजों को चेतावनी दी जा सके। (π = 3.14 का प्रयोग कीजिए)।
हल :
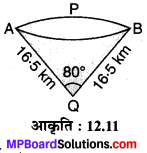
लाइट हाउस द्वारा जहाजों को दी जाने वाली चेतावनी के लिए क्षेत्रफल एक त्रिज्यखण्ड होगा जिसकी त्रिज्याएँ r = 16.5 km एवं त्रिज्याओं के बीच का कोण θ = 80° होगा।
चूँकि त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\theta}{360} \pi r^{2}\)
समुद्र के उस भाग का क्षेत्रफल = \(\frac{80^{\circ}}{360^{\circ}}\) x 3.14 x 16.5 x 16.5 .
= 6.28 x 5.5 x 5.5
= 189.97 km²
अतः समुद्र के भाग का अभीष्ट क्षेत्रफल = 189.97 km² है।
![]()
प्रश्न 13.
एक गोल मेजपोश पर छः समान डिजाइन बने हुए हैं, जैसा कि संलग्न आकृति 12.12 में दर्शाया गया है। यदि मेजपोश की त्रिज्या 28 cm है, तो Rs 0.35 प्रतिवर्ग सेण्टीमीटर की दर से इन डिजाइनों को बनाने की लागत ज्ञात कीजिए। (√3 = 1.7 का प्रयोग कीजिए।)
हल :
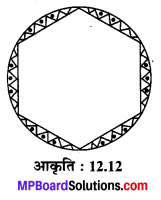
मेजपोश कुल छः बराबर त्रिज्यखण्डों में विभक्त है जिनकी त्रिज्या 28 cm तथा त्रिज्याओं के बीच कोण \(\frac { 360 }{ 6 }\) = 60° होगा।
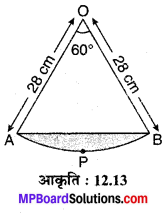
मान लीजिए कि एक त्रिज्यखण्ड OAPB संलग्न आकृति 12.13 में दिखाया गया है।
∆OAB एक समबाहु त्रिभुज है जिसकी भुजा 28 cm है।
[क्योंकि ∠AOB = 60° एवं ∠OAB = ∠OBA = 60°]
समबाहु त्रिभुज OAB का क्षेत्रफल = \(\frac{\sqrt{3}}{4}\) x (28)²
ar (OAB) = 333.2 cm² …(1)
त्रिज्यखण्ड OAPB का क्षेत्रफल = \(\frac{\theta}{360^{\circ}} \times \pi r^{2}\)
ar (OAPH) = \(\frac{60^{\circ}}{360^{\circ}} \times \frac{22}{7}(28 \times 28)\)
= \(\frac{22 \times 56}{3} \mathrm{cm}^{2}\)
= 410.67 cm²
वृत्तखण्ड का क्षेत्रफल = ar (OAPB) – ar (OAB)
= 410.67 – 333.2
= 77.47
6 वृत्तखण्डों का कुल क्षेत्रफल = 6 x 77.47 = 464.82 cm²
डिजाइन बनाने की लागत = दर x कुल क्षेत्रफल
= 0.35 x 464.82
= Rs 162.68
अत: अभीष्ट लागत = Rs 162.68 है।
प्रश्न 14.
निम्नलिखित में सही उत्तर चुनिए : त्रिज्या R वाले वृत्त के उस त्रिज्यखण्ड का क्षेत्रफल जिसका कोण P° है, निम्नलिखित है :

उत्तर-
(D) \(\frac{P}{720} \times 2 \pi R^{2}\)
![]()