MP Board Class 9th Maths Solutions Chapter 7 Triangles Ex 7.2

MP Board Class 9th Maths Solutions Chapter 7 Triangles Ex 7.2

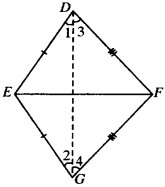
Question 1.
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:

1. OB = OC
2. AO bisect ∠A.

Solution:
Given
AB = AC
∠1 = ∠2, ∠3 = ∠4
To prove:

1. OB = OC
2. ∠5 = ∠6

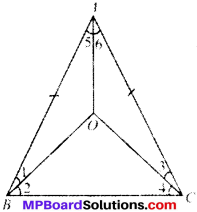
Proof:
In ∆ABC,
AB = AC
∠B = ∠C
\(\frac{1}{2}\) ∠B = \(\frac{1}{2}\) ∠C
∠1 = ∠3 or ∠2 = ∠4
In ∆OBC
∠2 = ∠4
and so OB = OC
(In a A, sides opposite to equal angles are equal)
In ∆ABO and ∆ACO
BO = CO (proved)
∠1 = ∠3 (proved)
AB = AC (given)
∆ABO = ∆ACO (by SAS)
and so ∠5 = ∠6 (by CPCT)

Question 2.
In ∆ABC, AD is the perpendicular bisector of BC (see Fig. below). Show that AABC is an isosceles triangle in which AB =AC.

Solution:
Given
∠ABC = ∠ADC
To prove:
AB = AC
Proof:
In A ABD and A ACD
BD = CD (given)
∠ADB = ∠ADC (given each 90°)
AD = AD (common)
∴ ∆ABD = ∆ACD (BySAS)
and so AB = AC (by CPCT)

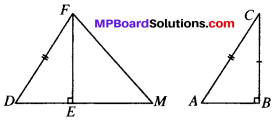
Question 3.
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. below). Show that these altitudes are equal.

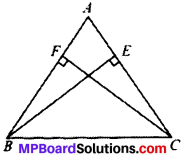
Solution:
Given
AB = AC
∠E = ∠F (each 90°)
To prove: BE = CF
Proof:
In ∆ABE and ∆ACE
∠A = ∠A (common)
∠E = ∠F (each 90°)
AB = AC (given)
∆ABE = ∆ACE (byAAS)
and so BE = CF (by CPCT)

Question 4.
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. below). Show that:

1. ∆ABE ≅ ∆ACF
2. AB = AC,

i. e., ABC is an isosceles triangle.

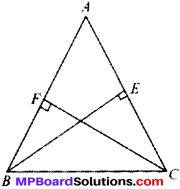
Solution:
Given
BE = CF
∠E = ∠F (each 90°)
To prove:

1. ∆ABE = ∆ACE
2. AB = AC

Proof:
In ∆ABE and ∆ACF
∠A = ∠A (common)
BE = CF (given)
∠E = ∠F (each 90°)
∆ABE = ∆ACF (by AAS)
and so AB = AC (by CPCT)

Question 5.
ABC and DBC are two isosceles triangles on the same base BC (see Fig. below). Show that ∠ABD = ∠ACD.

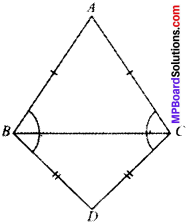
Solution:
Given
AB = AC
BD = CD
To prove
∠ABD = ∠ACD
Construction: Join AD
Proof:
In ∆ABD and ∆ACD
AD = AD (common)
AB = AC (given)
BD = CD (given)
∆ABD = ∆ACD (by SSS)
and so ∠ABD = ∠ACD (by CPCT)

Question 6.
∆ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig. below). Show that ∠BCD is a right angle.
Solution:
Given: AB = AC
AD = AB
To show: ∠BCD = 90°
i.e., ∠2 + ∠3 = 90°

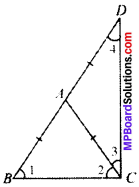
Proof:
AB = AC …..(1)
AB = AD …..(2)
From (1) and (2), we get
AC = AD
In ∆ABC
AB = AC
∠1 = ∠2
(In a A, angles opposite to equal sides are always equal) …p) …(3)
In ∆ACD
AC = AD
∠3 = ∠4
(In a A, angles opposite to equal sides are always equal) …(4)
In ∆BCD
∠1 + ∠2 + ∠3 + ∠4 = 180° (ASP)
∠2 + ∠2 + ∠3 + ∠3 = 180°
(∴ ∠1 = ∠2, ∠3 = ∠4)
2 (∠2 + ∠3) = 180°
(∠2 + ∠3) = 90°
∠BCD = 90°

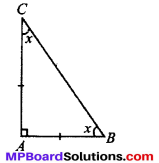
Question 7.
ABC is a right angled triangle in which ∠A – 90° and AB = AC. Find ∠B and ∠C.
Solution:
In ∆BAC
AB =AC
∠B = ∠C = x
∠A + ∠B + ∠C= 180°
∠B + ∠C = 180° – 90°
∠B + ∠C = 90°
2x = 90°
x = \(\frac{90^{\circ}}{2}\)

Question 8.
Show that the angles of an equilateral triangle are 60° each.
Solution:
Given
ABC is an equilateral ∆
i. e., AB = BC = AC
To prove
∠A = ∠B = ∠C = 60°
Proof:
In ∆BAC
AB = AC
∠B = ∠C
(In a A, angles opposite to equal sides are always equal) ……(1)
AC = BC
∠A = ∠B
(In a A, angles opposite to equal sides are always equal) …..(2)
From (1) and (2), we get,

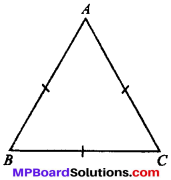
∠A = ∠B = ∠C = x (say)
∠A + ∠B + ∠C = 180° (ASP)
⇒ x + x + x = 180°
⇒ 3x = 180°
⇒ x = \(\frac{180^{\circ}}{3}\) = 60°
∴ ∠A = ∠B = ∠C = 60

Theorem 7.4.
SSS (Side-Side-Side) Congruence Theorem:
Two triangles are congruent if the three sides of one triangle are equal to the corresponding three sides of the other triangle.
Given
In ∆s ABC and DEF we have,

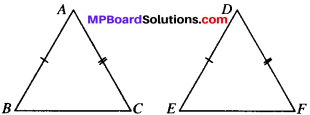
AB =DE
BC = EE
and AC = DF
To prove:
∆ABC = ∆DEF
Construction:
Suppose BC is the longest side.
Draw EF such that EE = AB and FEG = ∠CBA.
Join GF and DG.

Proof:
In ∆s ABC and GEE, we have
AB = GE (Const.)
∠ABC = ∠GEF (Const.)
and BC = EF (Given)
∴ ∆ABC = ∆GEF (SAS Cong. Axiom)
∠A = ∠G (CPCT) …..(1)
and AC = GF (CPCT) …..(2)
Now AB = EG (Const.)
AB = DE (Given)
∴ DE = EG ……(3)
Similarly, DF = GF ……(4)
In ∆EDG
DE = EG (Proved above)
∴ ∠A = ∠2 (∠s opp. equal side) …..(5)
In ∆DFG
FD = FG (Proved above)
∴ ∠3 = ∠4 (∠s ppp. equal side) …..(6)
∴ ∠1 + ∠3 – ∠2 + ∠4 [From (5) and (6)]
i. e. ∠D = ∠G …..(7)
But ∠G = ∠A [From (1)]
∴ ∠A = ∠D …..(8)
In ∆s ABC and DEF,
AB – DE (Given)
AC = DF (Given)
∠A = ∠D [From (8)]
∆ABC ≅ ∆DEF (SAS Cong. Axiom)

Theorem 7.5.
RHS (Right Angle Hypotenuse Side) Congruence Theorem:
Two right triangles are congruent if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and the corresponding side of the other triangle.
Given
In ∆s ABC and DEF,
∠B = ∠E = 90°
AC = DF
BC = EF.

∆ABC ≅ ∆DEF
Construction:
Produce DE to M so that
EM = AB, Join ME.
Proof:
In ∆s ABC and MEF
AB = ME (Const.)
BC = EE (Given)
∠B = ∠MEF (each 90°)
∴ ∆ABC = ∆MEF (SAS Cong. Axiom)
Hence ∠A = ∠M (CPCT) …(1)
AC = MF (CPCT) …(2)
Also AC =DF (Given)
∴ DF = MF
∴ ∠D = ∠M (∠s opp. equal side of ADFM) …(3)
From (1) and (3), we have
∠A = ∠D …..(4)
Now, in ∆s ABC and DEF, we have
∠A = ∠D [From (4)]
∠B = ∠E (Given)
∴ ∠C = ∠F …..(5)
Again, in ∆s ABC and DEF, we have
BC = EF (Given)
AC = DF (Given)
∠C = ∠F [From (5)]
∴ ∆ABC = ∆DEF (SAS Cong. Axiom)

MP Board Class 9th Maths Solutions