MP Board Class 9th Maths Solutions Chapter 15 प्रायिकता Additional Questions
MP Board Class 9th Maths Chapter 15 अतिरिक्त परीक्षोपयोगी प्रश्न
MP Board Class 9th Maths Chapter 15 दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
दो पाँसों को एक साथ 500 बार फेंका जाता है। प्रत्येक बार उनके ऊपर आई संख्याओं के योग को ज्ञात करके नीचे दी गई सारणी के अनुसार रिकॉर्ड किया गया है
| योग | बारम्बारता |
| 2 3 4 5 6 7 8 9 10 11 12 |
14 30 42 55 72 75 70 53 46 28 15 |
यदि इन पाँसों को एक बार पुनः फेंका जाए तो निम्नलिखित योग ज्ञात करने की क्या प्रायिकता है ?
(i) 3,
(ii) 10 से अधिक,
(iii) 5 से कम या उसके बराबर,
(iv) 8 और 12 के बीच।
हल :
(i) चूँकि E1 = 30 एवं n = 500 (प्रश्नानुसार)
प्रायिकता \(P\left(E_{1}\right)=\frac{E_{1}}{n}=\frac{30}{500}=0 \cdot 060\)
अतः अभीष्ट प्रायिकता = 0.060.
(ii) चूँकि E2 = 10 से अधिक योग वाले = 28 + 15 = 43 एवं n = 500
प्रायिकता \(P\left(E_{2}\right)=\frac{E_{2}}{n}=\frac{43}{500}=0 \cdot 086\)
अतः अभीष्ट प्रायिकता = 0.086.
(iii) 5 से कम या बराबर E3 = 55 + 42 + 30 + 14 = 141 एवं n = 500 (प्रश्नानुसार)
प्रायिकता \(P\left(E_{3}\right)=\frac{E_{3}}{n}=\frac{141}{500}=0.282\)
अतः अभीष्ट प्रायिकता = 0.282.
(iv) 8 और 12 के मध्य संख्याओं का योग = 53 + 46 + 28 = 127
इस प्रकार E4 = 127 एवं n = 500
प्रायिकता \(P\left(E_{4}\right)=\frac{E_{4}}{n}=\frac{127}{500}=0 \cdot 254\)
अतः अभीष्ट प्रायिकता = 0.254.
प्रश्न 2.
पिछले 200 कार्य दिवसों में किसी मशीन द्वारा निर्मित खराब पुों की संख्या निम्नलिखित सारणी में दी गई है:
| खराब पुजों की संख्या | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| दिन | 50 | 32 | 22 | 18 | 12 | 12 | 10 | 10 | 10 | 8 | 6 | 6 | 2 | 2 |
इनकी प्रायिकता निर्धारित कीजिए कि कल के उत्पादन में :
(i) कोई खराब पुर्जा नहीं होगा,
(ii) न्यूनतम एक खराब पुर्जा होगा,
(iii) 5 से अधिक खराब पुर्जे नहीं होंगे,
(iv) 13 से अधिक खराब पुर्जे नहीं होंगे।
हल :
(i) चूँकि E1 = शून्य खराब पुर्जे = 50 एवं n = 200
प्रायिकता \(P\left(E_{1}\right)=\frac{E_{1}}{n}=\frac{50}{200}=0 \cdot 25\)
अतः अभीष्ट प्रायिकता = 0.25.
(ii) न्यूनतम एक खराब पुर्जा = 200 – 50 = 150
E2 = 150 एवं n = 200
प्रायिकता \(P\left(E_{2}\right)=\frac{E_{2}}{n}=\frac{150}{200}=0 \cdot 75\)
अतः अभीष्ट प्रायिकता = 0.75.
(iii) 5 से अधिक खराब पुर्जे नहीं होंगे अर्थात् 5 तक खराब पुर्जे होंगे जिनका योग E3 = 50 + 32 + 22 + 18 + 12 + 12 = 146 एवं n = 200 (प्रश्नानुसार)
प्रायिकता \(P\left(E_{3}\right)=\frac{E_{3}}{n}=\frac{146}{200}=0 \cdot 73\)
अतः अभीष्ट प्रायिकता = 0.73.
(iv) चूँकि 13 से अधिक खराब पुर्जे नहीं हैं E4 = 0 एवं n = 200
प्रायिकता \(P\left(E_{4}\right)=\frac{E_{4}}{n}=\frac{0}{200}=0\)
अतः अभीष्ट प्रायिकता = 0.
प्रश्न 3.
कुछ समय पहले ही किए गए एक सर्वेक्षण में यह पाया गया कि एक फैक्टरी के श्रमिकों की आयु का बंटन निम्नलिखित है:
| आयु (वर्षों में) | 20 – 29 | 30 – 39 | 40 – 49 | 50 – 59 | 60 और उससे ऊपर |
| श्रमिकों की संख्या | 38 | 27 | 86 | 46 | 3 |
यदि इनमें से एक व्यक्ति यदृच्छिक रूप से चुना जाता है तो इसकी क्या प्रायिकता है कि वह व्यक्ति:
(i) 40 वर्ष या उससे अधिक आयु का होगा ?
(ii) 40 वर्ष से कम आयु का होगा?
(iii) 30 और 39 वर्ष के बीच की आयु का होगा?
(iv) 60 वर्ष से कम आयु का होगा परन्तु 39 वर्ष से अधिक होगा?
हल :
प्रत्येक स्थिति से कुल श्रमिकों की संख्या (n) = 38 + 27 + 86 + 46 + 3
n = 200 .
(i) 40 वर्ष या उससे अधिक श्रमिक (E1) = 86 + 46 + 3 = 135
प्रायिकता \(P\left(E_{1}\right)=\frac{E_{1}}{n}=\frac{135}{200}=0 \cdot 675\)
अतः अभीष्ट प्रायिकता = 0.675.
(ii) 40 वर्ष से कम आयु के श्रमिकों की संख्या (E2) = 38 + 27 = 65
प्रायिकता \(P\left(E_{2}\right)=\frac{E_{2}}{n}=\frac{65}{200}=0 \cdot 325\)
अतः अभीष्ट प्रायिकता = 0.325.
(iii) 30 और 39 वर्ष के बीच श्रमिकों की संख्या (E3) = 27
प्रायिकता \(P\left(E_{3}\right)=\frac{E_{3}}{n}=\frac{27}{200}=0 \cdot 135\)
अतः अभीष्ट प्रायिकता = 0.135.
(iv) 60 वर्ष से कम और 39 वर्ष से अधिक आयु के श्रमिकों की संख्या (E4) = 86 + 46 = 132
प्रायिकता \(P\left(E_{4}\right)=\frac{E_{4}}{n}=\frac{132}{200}=0 \cdot 66\)
अतः अभीष्ट प्रायिकता = 0.66.
प्रश्न 4.
एक पाँसे को 1000 बार फेंकने पर प्राप्त परिणामों की सारणी इस प्रकार हैं:
| परिणाम | 1 | 2 | 3 | 4 | 5 | 6 |
| बारम्बारता | 180 | 150 | 160 | 170 | 150 | 190 |
प्रत्येक परिणाम के प्राप्त होने की प्रायिकता ज्ञात कीजिए। (2019)
हल :
ज्ञात है : n (E) = 1000 तो प्रश्नानुसार,
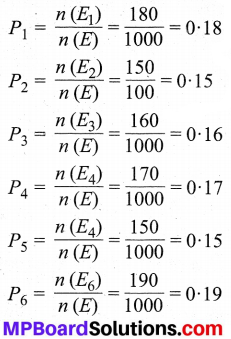
अतः अभीष्ट प्रायिकताएँ हैं : P1 = 0.18, P2 = 0.15, P3 = 0.16, P4 = 0.17, P5 = 0.15 एवं P6 = 0.19.
![]()
MP Board Class 9th Maths Chapter 15 लघु उत्तरीय प्रश्न
प्रश्न 1.
यहाँ एक जन्म-मृत्यु दर सारणी का एक अंश दिया गया है:
| आयु (वर्षों में) | 60 | 61 | 62 | 63 | 64 | 65 |
| जीवित व्यक्तियों की संख्या एक मिलियन के प्रतिदर्श में से | 16,090 | 11,490 | 8,012 | 5,448 | 3,607 | 2,320 |
(i) इस सूचना के आधार पर 60 वर्ष की आयु के व्यक्ति की एक वर्ष के अन्दर मृत्यु हो जाने की प्रायिकता क्या है ?
(ii) इसकी प्रायिकता क्या है कि 61 वर्ष की आयु वाला व्यक्ति 4 वर्ष तक जीवित रहेगा ?
हल :
(i) हम देखते हैं कि 60 वर्ष की आयु वाले कुल 16,090 व्यक्तियों में से (16,090 – 11,490)
अर्थात् 4,600 व्यक्ति 61वें वर्ष के होने से पहले ही मृत्यु को प्राप्त हो जाते हैं। यहाँ E1 = 4600 एवं n = 16,090 है।
प्रायिकता \(P\left(E_{1}\right)=\frac{E_{1}}{n}=\frac{4600}{16,090}=\frac{460}{1,609}\)
अतः 60 वर्ष की आयु के व्यक्ति को एक वर्ष के अन्दर मृत्यु हो जाने की अभीष्ट प्रायिकता = \(\frac { 460 }{ 1609 }\)
(ii) 61 वर्ष की आयु वाले व्यक्तियों की संख्या = 11,490, इनमें से चार वर्ष तक जीवित बचने वाले व्यक्तियों की संख्या = 2,320 अर्थात् E2 = 2320 एवं n = 11,490
प्रायिकता \(P\left(E_{2}\right)=\frac{E_{2}}{n}=\frac{2,320}{11,490}=\frac{232}{1,149}\)
अतः 61 वर्ष की आयु वाले व्यक्ति के 4 वर्ष तक जीवित रहने की अभीष्ट प्रायिकता = \(\frac { 232 }{ 1149 }\)
प्रश्न 2.
एक कम्पनी ने 4,000 परिवारों को यदृच्छिक रूप से चुना तथा उनके आय स्तर और घर में स्थित टी. वी. सेटों की संख्या में सम्बन्ध ज्ञात करने हेतु एक सर्वेक्षण किया। इस प्रकार प्राप्त सूचनाओं को निम्नलिखित सारणी के रूप में सूचीबद्ध किया गया है :
| मासिक आय (Rs में) | टी.वी. सेटों/परिवारों की संख्या | |||
| 0 | 1 | 2 | 2 से अधिक | |
| <10,000 10,000 – 14,999 15,000 – 19,999 20,000 – 24,999 25,000 और उससे अधिक |
20 10 0 0 0 |
80 240 380 520 1100 |
10 60 120 370 760 |
0 0 30 80 720 |
निम्नलिखित की प्रायिकता ज्ञात कीजिए :
(i) एक परिवार की आय Rs 10,000 से Rs 14,999 होने और घर में ठीक एक टी. वी. सेट होना।
(ii) एक परिवार की आय Rs 25,000 और उससे अधिक होने और घर में दो टी. वी. सेट होना।
(iii) एक परिवार में एक भी टी. वी. सेट नहीं होना।
हल :
(i) चूँकि यहाँ E1 = 240 एवं n= 4,000 (प्रश्नानुसार)
प्रायिकता \(P\left(E_{1}\right)=\frac{E_{1}}{n}=\frac{240}{4,000}=\frac{3}{50}\)
अतः अभीष्ट प्रायिकता = \(\frac { 3 }{ 50 }\)
(ii) चूँकि यहाँ E2 = 760 एवं n = 4,000 (प्रश्नानुसार)
प्रायिकता \(P\left(E_{2}\right)=\frac{E_{2}}{n}=\frac{760}{4,000}=\frac{19}{100}\)
अतः अभीष्ट प्रायिकता = \(\frac { 19 }{ 100 }\)
(iii) चूँकि E3 = बिना टी. वी वाले परिवार = 20 + 10 = 30 एवं n = 4,000
प्रायिकता \(P\left(E_{3}\right)=\frac{E_{3}}{n}=\frac{30}{4,000}=\frac{3}{400}\)
अतः अभीष्ट प्रायिकता = \(\frac { 3 }{ 400 }\)
प्रश्न 3.
पैक किए गए प्रत्येक डिब्बे में बल्बों की संख्या 90 है। इनमें से 700 डिब्बों के खराब बल्बों की संख्या ज्ञात करने के लिए जाँच की गई तथा इसके परिणाम निम्नलिखित सारणी में दिए गए हैं:
| खराब बल्बों की संख्या | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 6 से अधिक |
| बारम्बारता | 400 | 180 | 48 | 41 | 18 | 8 | 3 | 2 |
इन डिब्बों में से एक डिब्बा यादृच्छिक रूप से चुना जाता है। इसकी क्या प्रायिकता है कि इस डिब्बे में:
(i) कोई बल्ब खराब नहीं होगा ?
(ii) खराब बल्बों की संख्या 2 से 6 तक होगी ?
(iii) 4 से कम खराब बल्ब होंगे ?
हल :
(i) यहाँ n = 700 एवं E1 = शून्य खराब बल्ब वाले डिब्बे = 400
प्रायिकता \(P\left(E_{1}\right)=\frac{E_{1}}{n}=\frac{400}{700}=\frac{4}{7}\)
अतः अभीष्ट प्रायिकता = \(\frac { 4 }{ 7 }\)
(ii) यहाँ n = 700 एवं E2 = 2 से 6 तक खराब बल्बों वाले डिब्बों की कुल संख्या
E2 = 48 + 41 + 18 + 8 + 3 = 118
प्रायिकता \(P\left(E_{2}\right)=\frac{E_{2}}{n}=\frac{118}{700}=\frac{59}{350}\)
अतः अभीष्ट प्रायिकता = \(\frac { 59 }{ 350 }\)
(iii) यहाँ n = 700 एवं E3 = 4 से कम खराब बल्बों वाले डिब्बों की संख्या
E3 = 400 + 180 + 48 + 41 = 669
प्रायिकता \(P\left(E_{3}\right)=\frac{E_{3}}{n}=\frac{669}{700}\)
अतः अभीष्ट प्रायिकता = \(\frac { 669 }{ 700 }\)
![]()
MP Board Class 9th Maths Chapter 15 अति लघु उत्तरीय प्रश्न
प्रश्न 1.
क्या किसी घटना की प्रायोगिक प्रायिकता एक ऋणात्मक संख्या हो सकती है ? यदि नहीं तो क्यों?
उत्तर-
प्रायिकता ऋणात्मक संख्या नहीं हो सकती, क्योंकि उन अभिप्रयोगों की जिनमें कोई घटना हो सकती है, ऋणात्मक नहीं हो सकती तथा कुल अभिप्रयोगों की संख्या भी ऋणात्मक नहीं हो सकती।
प्रश्न 2.
क्या किसी घटना की प्रायोगिक प्रायिकता 1 से अधिक हो सकती है ? अपने उत्तर का औचित्य दीजिए।
उत्तर-
किसी घटना की प्रायोगिक प्रायिकता 1 से अधिक कभी भी नहीं हो सकती, क्योंकि उन अभिप्रयोगों की संख्या जिनमें कोई घटना हो सकती है कभी भी अभिप्रयोगों की कुल संख्या से अधिक नहीं हो सकती।
प्रश्न 3.
जैसे-जैसे एक सिक्के के उछालों की संख्या बढ़ती जाती है चितों की संख्या और पटों की संख्या का अनुपात \(\frac { 1 }{ 2 }\) हो जाता है। क्या यह सही है ? यदि नहीं तो इसे सही रूप में लिखिए।
उत्तर-
कथन असत्य है, क्योंकि जैसे-जैसे एक सिक्के के उछालों की संख्या बढ़ती जाती है, वैसे-वैसे चितों की संख्या और कुल उछालों की संख्या में \(\frac { 1 }{ 2 }\) के निकटतम होता जाता है, ठीक \(\frac { 1 }{ 2 }\) नहीं होता।
![]()
MP Board Class 9th Maths Chapter 15 वस्तुनिष्ठ प्रश्न
बहु-विकल्पीय प्रश्न
प्रश्न 1.
एक पाँसे को 1000 बार फेंका गया और परिणाम निम्नलिखित प्रकार से रिकॉर्ड किए गए:
| परिणाम | 1 | 2 | 3 | 4 | 5 | 6 |
| बारम्बारता | 180 | 150 | 160 | 170 | 150 | 190 |
यदि पाँसे को एक बार और फेंका जाए तो इसकी प्रायिकता कि यह 5 दर्शाएगा :
(a) \(\frac { 9 }{ 50 }\)
(b) \(\frac { 3 }{ 20 }\)
(c) \(\frac { 4 }{ 25 }\)
(d) \(\frac { 7 }{ 25 }\)
उत्तर:
(b) \(\frac { 3 }{ 20 }\)
प्रश्न 2.
642 व्यक्तियों पर किए गए एक प्रतिदर्श अध्ययन में यह पाया गया कि 514 व्यक्तियों के पास हाईस्कूल सर्टिफिकेट हैं। यदि इनमें से एक व्यक्ति को यादृच्छिक रूप से चुना जाए तो इसकी प्रायिकता कि उस व्यक्ति के पास हाईस्कूल सर्टिफिकेट है:
(a) 0.5
(b) 0.6
(c) 0.7
(d) 0.8.
उत्तर:
(d) 0.8.
प्रश्न 3.
19 – 36 महीने की आयु वाले 364 बच्चों पर किए गए एक सर्वे में यह पाया गया कि 91 बच्चे आलू के चिप्स खाना पसंद करते हैं। इनमें से एक बच्चा यदि यादृच्छिक रूप से चुना जाता है, तो इसकी प्रायिकता कि वह बच्चा आलू के चिप्स पसंद नहीं करेगा, है :
(a) 0.25
(b) 0.50
(c) 0.75
(d) 0.80.
उत्तर:
(c) 0.75
प्रश्न 4.
किसी कक्षा के विद्यार्थियों की एक मेडीकल परीक्षा में निम्नलिखित रक्त समूह रिकॉर्ड किए गए:
| रक्त समूह | A | AB | B | O |
| विद्यार्थियों की संख्या | 10 | 13 | 12 | 5 |
इस कक्षा में से एक विद्यार्थी यादृच्छिक रूप से चुना जाता है। इस विद्यार्थी का रक्त समूह B होने की प्रायिकता है:
(a) \(\frac { 1 }{ 4 }\)
(b) \(\frac { 13 }{ 40 }\)
(c) \(\frac { 3 }{ 10 }\)
(d) \(\frac { 1 }{ 8 }\)
उत्तर:
(c) \(\frac { 3 }{ 10 }\)
प्रश्न 5.
दो सिक्कों को 1000 बार उछाला जाता है और इनके परिणाम निम्नलिखित प्रकार से रिकॉर्ड किए जाते हैं:
| चितों की संख्या | 2 | 1 | 0 |
| बारम्बारता | 200 | 550 | 250 |
इस सूचना के आधार पर अधिकतम एक चित की प्रायिकता है :
(a) \(\frac { 1 }{ 5 }\)
(b) \(\frac { 1 }{ 4 }\)
(c) \(\frac { 4 }{ 5 }\)
(d) \(\frac { 3 }{ 4 }\)
उत्तर:
(c) \(\frac { 4 }{ 5 }\)
![]()
प्रश्न 6.
एक संग्रह में से 80 बल्ब यदृच्छिक रूप से चुने जाते हैं और उनके जीवनकालों (घण्टों में) को निम्नलिखित बारम्बारता सारणी के रूप में रिकॉर्ड किया गया:
| जीवनकाल (घण्टों से) | 300 | 500 | 700 | 900 | 1100 |
| बारम्बारता | 10 | 12 | 23 | 25 | 10 |
इस संग्रह में से एक बल्ब यादृच्छिक रूप से चुना जाता है। इस बल्ब का जीवनकाल 1150 घण्टा होने की प्रायिकता है:
(a) \(\frac { 1 }{ 80 }\)
(b) \(\frac { 7 }{ 16 }\)
(c) 0
(d) 1
उत्तर:
(c) 0
प्रश्न 7.
एक संग्रह में से 80 बल्ब यदृच्छिक रूप से चुने जाते हैं और उनके जीवनकालों (घण्टों में) को निम्नलिखित बारम्बारता सारणी के रूप में रिकॉर्ड किया गया:
| जीवनकाल (घण्टों से) | 300 | 500 | 700 | 900 | 1100 |
| बारम्बारता | 10 | 12 | 23 | 25 | 10 |
इस संग्रह में से एक बल्ब यदृच्छिक रूप से चुने जाने पर इसका जीवनकाल 900 घण्टे से कम होने की प्रायिकता है:
(a) \(\frac { 11 }{ 40 }\)
(b) \(\frac { 5 }{ 16 }\)
(c) \(\frac { 7 }{ 16 }\)
(d) \(\frac { 9 }{ 16 }\)
उत्तर:
(d) \(\frac { 9 }{ 16 }\)
प्रश्न 8.
एक सिक्के को उछालने पर हैड (चित) आने की प्रायिकता है :
(a) 0
(b) 3
(c) \(\frac { 1 }{ 2 }\)
(d) \(-\frac { 1 }{ 3 }\)
उत्तर:
(c) \(\frac { 1 }{ 2 }\)
प्रश्न 9.
किसी घटना के घटित होने की सम्भावनाओं के परिणाम को कहते हैं
(a) मध्यमान
(b) आवृत्ति
(c) परास
(d) प्रायिकता।
उत्तर:
(d) प्रायिकता।
प्रश्न 10.
एक सिक्के के एक बार उछालने पर पट आने से प्रायिकता होगी :
(a) \(\frac { 1 }{ 4 }\)
(b) \(\frac { 1 }{ 2 }\)
(c) 1
(d) \(\frac { 3 }{ 4 }\)
उत्तर:
(b) \(\frac { 1 }{ 2 }\)
प्रश्न 11.
किसी पाँसे की फेंक में 7 आने की प्रायिकता होगी :(2019)
(a) \(\frac { 1 }{ 6 }\)
(b) 1
(c) 0
(d) \(\frac { 1 }{ 7 }\)
उत्तर:
(c) 0
![]()
रिक्त स्थानों की पूर्ति
1. दो सिक्कों को एक साथ उछालने पर कम-से-कम एक चित आने की प्रायिकता ………… होगी। (2018)
2. एक घनाकार पाँसे को फेंकने पर विषम अंक आने की प्रायिकता ………… होगी।
3. सभी सम्भव प्रायिकताओं का योग सदैव …………. होता है।
4. किसी भी घटना के न घटने की प्रायिकता सदैव ……….. होती है।
5. एक सिक्के को असंख्य बार फेंकने पर पट आने की प्रायिकता ……….. होती है।
6. किसी पाँसे के फेंकने पर 1 अंक ऊपर आने की प्रायिकता ……….. होती है। (2019)
7. किसी असम्भव घटना की प्रायिकता ……….. होती है। (2019)
उत्तर-
1. \(\frac { 3 }{ 4 }\)
2. \(\frac { 1 }{ 2 }\)
3. 1,
4. 0 (शून्य),
5. \(\frac { 1 }{ 2 }\)
6. \(\frac { 1 }{ 6 }\)
7. 0 (शून्य)।
जोड़ी मिलान

उत्तर-
1. (c)
2. (d)
3. (e)
4. (a)
5. (b).
सत्य/असत्य कथन
1. किसी घटना की प्रायिकता का मान ऋणात्मक भी हो सकता है।
2. एक पाँसे को फेंकने पर उसके फलक पर 7 आने की प्रायिकता शून्य होती है।
3. किसी घटना की प्रायिकता एक से अधिक भी हो सकती है।
4. असम्भव घटनाओं की प्रायिकता सदैव एक होती है।
5. एक सिक्के को उछालने पर चित आने की प्रायिकता 1 होती है।
6. किसी निश्चित घटना की प्रायिकता सदैव एक होती है। (2019)
उत्तर-
1. असत्य,
2. सत्य,
3. असत्य,
4. असत्य,
5. असत्य,
6. सत्य।
![]()
एक शब्द/वाक्य में उत्तर
1. किसी घटना के घटित होने की सम्भावनाओं का परिमाणबोधक या संख्यात्मक निरूपण क्या कहलाता है? (2018)
2. किसी घटना के घटने की प्रायिकता क्या हो सकती है?
3. प्रायिकता का अनुप्रयोग किस क्षेत्र में किया जाता है।
4. किसी पाँसे को फेंकने पर फलक पर 7 का अंक आने की प्रायिकता क्या होगी?
5. प्रायिकता का सूत्र लिखिए।
6. एक निश्चित घटना की प्रायिकता क्या होगी? (2019)
7. एक सिक्का उछाला गया, तब हेड आने की प्रायिकता क्या होगी? (2019)
8. किसी पासे की फेंक में अंक 2 आने की प्रायिकता क्या होगी? (2019)
उत्तर-
1. प्रायिकता,
2. 0 से 1 के बीच (जिसमें 0 और 1 भी सम्मिलित हैं) होती है,
3. भौतिकी, वाणिज्य, जीव विज्ञान, खगोलशास्त्र, ज्योतिष और मौसम विभाग में,
4. शून्य,
5.

6.1 (एक),
7. \(\frac { 1 }{ 2 }\)
8. \(\frac { 1 }{ 6 }\)