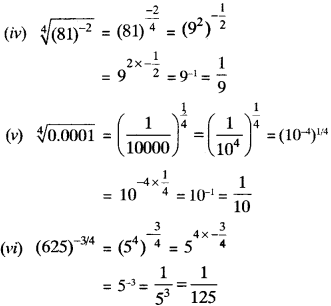MP Board Class 9th Maths Solutions Chapter 1 Number Systems Ex 1.5
Question 1.
Classify the following numbers as rational or irrational –
- 2 – √5
- (3 + \(\sqrt{23}\) ) – \(\sqrt{23}\)
- \(\frac { 2\sqrt { 7 } }{ 7\sqrt { 7 } } \)
- \(\frac{1}{sqrt { 2 }}\)
- 2π
Solution:
- 2 – \(\sqrt{5}\) is an irrational number
- (3 + \(\sqrt{23}\) ) – \(\sqrt{23}\) = 3 is a rational number
- \(\frac { 2\sqrt { 7 } }{ 7\sqrt { 7 } } \) = \(\frac{2}{7}\) is a rational number
- \(\frac{1}{\sqrt { 2 }}\) = is an irrational number
- 2π is an irrational number.
![]()
Question 2.
Simplify each of the following expressions –
- (3 + \(\sqrt{3}\) ) (2 +\(\sqrt{2}\))
- (3 + \(\sqrt{3}\) ) (3 – \(\sqrt{3}\))
- (\(\sqrt{5}\) + \(\sqrt{2}\))2
- (\(\sqrt{5}\) – \(\sqrt{2}\)) (\(\sqrt{5}\) + \(\sqrt{2}\))
Solution:
1. (3 + \(\sqrt{3}\) ) (2 +\(\sqrt{2}\))
= 6 + 3\(\sqrt{2}\) + 2\(\sqrt{3}\) + \(\sqrt{6}\)
2. (3 + \(\sqrt{3}\)) (3 – \(\sqrt{3}\))
= (3)2 – (\(\sqrt{3}\) )2 = 9 – 3 = 6
3. (\(\sqrt{5}\) + \(\sqrt{2}\) )2
= (\(\sqrt{5}\))2 + 2\(\sqrt{5}\) x \(\sqrt{2}\) + (\(\sqrt{2}\))2
= 5 + 2\(\sqrt{10}\) + 2 = 7 + 2\(\sqrt{10}\)
4. (\(\sqrt{5}\) – \(\sqrt{2}\)) (\(\sqrt{5}\) + \(\sqrt{2}\))
= (\(\sqrt{5}\))2 – (\(\sqrt{2}\))2 = 5 – 2 = 3
Question 3.
Recall, 7t is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, π = \(\frac{c}{d}\). This seems to contradiet the fact n is irrational. How will you resolve this contradiction?
Solution:
No contradiction will be there. Whenever we measure any length with any device, we only get an approx, rational value and so cannot realise that either c or d is irrational.
![]()
Question 4.
Represent \(\sqrt{9.3}\) on the number line.
Solution:
Steps:
- Draw a line segment AC = 9.3 cm and extend it to B such that CB – 1 cm.
- Draw the perpendicular bisector of AS and mark the mid point O of AB.
- With O as centre and OB as radius, draw a semicircle.
- At point C, draw perpendicular CD which intersect the semicircle at D such that CD = \(\sqrt{9.3}\).
- With C as centre and CD as radius, draw an arc which intersect AB produced at E.
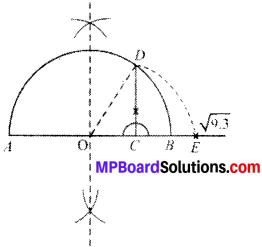
Proof:
OA = OB = \(\frac{10.3}{2}\) = 5.15cm
OD = 5.15 cm
OC = OB – BC = 5.15 – 1 = 4.15 cm
CD = \(\sqrt { OD^{ 2 }-OC^{ 2 } } \)
= \(\sqrt{9.3}\) cm
Question 5.
Rationalise the denominators of the following:
- \(\frac{1}{\sqrt { 7 }}\)
- \(\frac{1}{\sqrt{7}-\sqrt{6}}\)
- \(\frac{1}{\sqrt{5}+\sqrt{2}}\)
- \(\frac{1}{\sqrt{7}-2}\)
Solution:
1. \(\frac{1}{\sqrt { 7 }}\)

2. \(\frac{1}{\sqrt{7}-\sqrt{6}}\)
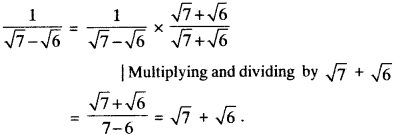
3. \(\frac{1}{\sqrt{5}+\sqrt{2}}\)

4. \(\frac{1}{\sqrt{7}-2}\)
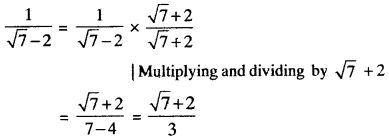
Laws of Exponents for real numbers:
If a, n and m are natural numbers, then
- am x an = am+n
- (am)n = amn
- \(\frac { a^{ m } }{ b^{ n } } \) where m > n
- am x bm – (ab)m
Example 1.
- 23 x 24 = 23+4 = 27
- (32)3 = 32×3 = 36
- \(\frac { 5^{ 5 } }{ 5^{ 2 } } \) = 55-2 = 53
- 23 x 33 = (2 x 3)3 = 63
![]()
Example 2.
1. 6\(\frac{2}{5}\) x 6\(\frac{3}{5}\)
Solution:
6\(\frac{2}{5}\) x 6\(\frac{3}{5}\) = 6\(\frac{5}{5}\) = 6
2. 6\(\frac{1}{2}\) x 7\(\frac{1}{2}\)
Solution:
6\(\frac{1}{2}\) x 7\(\frac{1}{2}\) = (6 x 7)\(\frac{1}{2}\) = 42\(\frac{1}{2}\)
3. \(\frac{5^{6 / 7}}{5^{2 / 3}}\)
Solution:
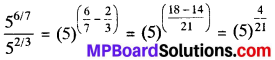
Example 3.
Simplify
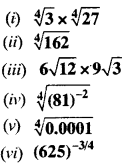
Solution: