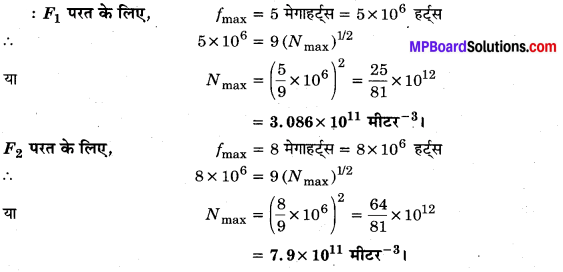MP Board Class 12th Physics Solutions Chapter 15 संचार व्यवस्था

MP Board Class 12th Physics Solutions Chapter 15 संचार व्यवस्था

 संचार व्यवस्था  NCERT पाठ्यपुस्तक के अध्याय में पाठ्यनिहित प्रश्न एवं उनके उत्तर

प्रश्न 1.
व्योम तरंगों के उपयोग द्वारा क्षितिज के पार संचार के लिए निम्नलिखित आवृत्तियों में से कौन-सी आवृत्ति उपयुक्त रहेगी?
(a) 10 किलोहर्ट्स
(b) 10 मेगाहर्ट्स
(c) 1 गीगाहर्ट्स
(d) 1000 गीगाहर्ट्स।
उत्तर
(b) 10 मेगाहर्ट्स।
3 मेगाहर्ट्स से 30 मेगाहर्ट्स आवृत्ति तक की तरंगें व्योम तरंगों की श्रेणी में आती हैं। इससे उच्च आवृत्ति की तरंगें (जैसे-1 गीगाहर्ट्स, 1000 गीगाहर्ट्स) आयन-मण्डल को भेदकर पार निकल जाती हैं, जबकि 10 किलोहर्ट्स आवृत्ति की तरंगें ऐन्टिना की ऊँचाई अधिक होने के कारण उपयोगी नहीं हैं।

प्रश्न 2.
UHF परिसर की आवृत्तियों का प्रसारण प्रायः किसके द्वारा होता है?
(a) भू-तरंगें
(b) व्योम तरंगें
(c) पृष्ठीय तरंगें
(d) आकाश तरंगें।
उत्तर
(d) आकाश तरंगें।
UHF परिसर में प्रसारण आकाश तरंगों द्वारा ही होता है।

प्रश्न 3.
अंकीय सिग्नल :
(i) मानों का संतत समुच्चय प्रदान नहीं करते
(ii) मानों को विविक्त चरणों के रूप में निरूपित करते हैं
(iii) द्विआधारी पद्धति का उपयोग करते हैं ।
(iv) दशमलव के साथ द्विआधारी पद्धति का भी उपयोग करते हैं।
उपर्युक्त प्रकथनों में कौन-से सत्य हैं?
(a) केवल (i) तथा (ii)
(b) केवल (ii) तथा (iii)
(c) (i), (ii) तथा (iii) परन्तु (iv) नहीं
(d) (i), (ii), (iii) तथा (iv) सभी।
उत्तर
(c).
अंकीय सिग्नल द्विआधारी पद्धति (अंकों 0 तथा 1) का उपयोग करते हैं। अत: मानों का सतत समुच्चय प्रदान करने के स्थान पर उन्हें विविक्त चरणों में निरूपित करते हैं।

प्रश्न 4.
दृष्टिरेखीय संचार के लिए क्या यह आवश्यक है कि प्रेषक ऐन्टीना की ऊँचाई अभिग्राही ऐन्टीना की ऊँचाई के बराबर हो? कोई TV प्रेषक ऐन्टीना 81 मीटर ऊँचा है। यदि अभिग्राही ऐन्टिना भूस्तर पर है तो यह कितने क्षेत्र में सेवाएँ प्रदान करेगा?
उत्तर
नहीं, दृष्टिरेखीय संचार हेतु प्रेषक ऐन्टिना की ऊँचाई अभिग्राही ऐन्टिना की ऊँचाई के बराबर होना आवश्यक नहीं है। दिया है,
प्रेषक ऐन्टिना की ऊँचाई h_T = 81 मीटर .
अभिग्राही ऐन्टिना की ऊँचाई h_R = 0
पृथ्वी की त्रिज्या R= 6.4×10⁶ मीटर
माना इस ऐन्टिना से d त्रिज्या के वृत्त में सेवाएँ प्राप्त की जा सकती हैं, तब
d = \(d=\sqrt{2 h_{T} R}+\sqrt{2 h_{R} R}=\sqrt{2 \times 81 \times 6.4 \times 10^{6}}+0\)
यदि ऐन्टिना A क्षेत्रफल में सेवाएँ प्रदान कर सकता है तो
A= πd² = 3.14 × 2 x 81 × 6.4 × 10⁶ मीटर ²
= 3255.55 किमी²

प्रश्न 5.
12 वोल्ट शिखर वोल्टता की वाहक तरंग का उपयोग किसी संदेश सिग्नल के प्रेषण के लिए किया गया है। मॉडुलन सूचकांक 75% के लिए मॉडुलक सिग्नल की शिखर वोल्टता कितनी होनी चाहिए?
हल :
वाहक तरंग की शिखर वोल्टता E_c = 12 वोल्ट
मॉडुलन सूचकांक μ = 75%
यदि मॉडुलक सिग्नल की शिखर वोल्टता E_m है तो
मॉडुलन सूचकांक \(\frac{E_{m}}{E_{c}}\) x 100 = 75
E_m = \(\frac { 75 }{ 100 }\)xE_c = \(\frac { 3 }{ 4 }\) x 12 = 9 वोल्ट
अत: मॉडुलक सिग्नल की शिखर वोल्टता = 9 वोल्ट।

प्रश्न 6.
चित्र-15.1 में दर्शाए अनुसार कोई मॉडुलक सिग्नलं वर्ग तरंग है। .

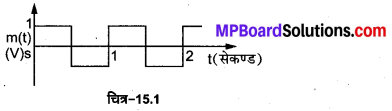
दिया गया है कि वाहक तरंग c(t) = 2sin (8 π t) वोल्ट

1. आयाम मॉडुलित तरंग रूप आलेखित कीजिए।
2. मॉडुलन सूचकांक क्या है?

हल
1. चित्र से स्पष्ट है कि 0 ≤ t ≤ 0.5 सेकण्ड
m(t) = 1 वोल्ट
c_m(t) = [A_c + m(t)] sin (8 π t)= 3 sin 8 π t [∵A_c = 2 वोल्ट]
0.5 सेकण्ड ≤ t ≤ 1.0 सेकण्ड
m(t) = – 1 वोल्ट
c_m (t) = [A_c + m (t)] sin (8 π t) = 1 sin (8 π t)
1.0 सेकण्ड ≤ t ≤ 1.5 सेकण्ड
m(t) = 1
c_m (t) = [A_c + m(t)] sin(8 π t)= 3 sin (8 π t)
तथा इसी प्रकार 1.5 सेकण्ड ≤ t ≤ 2.0 सेकण्ड
c_m (t) = 1 sin (8 π t)
अत: मॉडुलित तरंग को निम्न प्रकार से लिखा जा सकता है

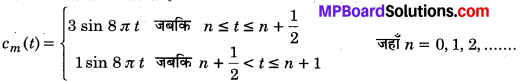
वाहक तरंग की कोणीय आवृत्ति ω_c= 8π
∵ \(T_{c}=\frac{2 \pi}{\omega_{c}}=\frac{1}{4}\) 1 सेकण्ड
∵ 1 सेकण्ड में वाहक तरंग के चार दोलन पूरे होंगे।
इनमें से प्रथम 2 दोलन (t= 0 से t = 0.5 सेकण्ड तक) तरंग c_m (t) = 3 sin 8 π t के होंगे तथा अगले दो दोलन C_m (t) = 1 sin 8 π t के होंगे।
इसी प्रकार के दोलन अगले 1 सेकण्ड में होंगे।

इस आधार पर मॉडुलित तरंग रूप निम्नलिखित है

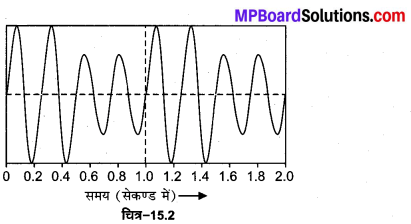
2. वाहक तरंग की शिखर वोल्टता E_c = 2 वोल्ट
मॉडुलक तरंग की शिखर वोल्टता E_m = 1 वोल्ट
मॉडुलन सूचकांक μ = \(\frac { E_m }{ E_m }\) = \(\frac { 1 }{ 2 }\) = 0.5
अथवा
μ = \(\frac { E_m }{ E_m }\) x 100% = 0.5 x 100% = 50%

प्रश्न 7.
किसी मॉडुलित तरंग का अधिकतम आयाम 10 वोल्ट तथा न्यूनतम आयाम 2 वोल्ट पाया जाता है। मॉडुलन । सूचकांक u का मान निश्चित कीजिए।
यदि न्यूनतम आयाम शून्य वोल्ट हो तो मॉडुलन सूचकांक क्या होगा?
हल :
दिया है, मॉडुलित तरंग का अधिकतम आयाम E_max = 10 वोल्ट, न्यूनतम आयाम E_min = 2 वोल्ट
यदि वाहक तरंग तथा मॉडुलक तरंग के आयाम क्रमश: E_c व E_m हैं तो

प्रश्न 8.
आर्थिक कारणों से किसी AM तरंग का केवल ऊपरी पार्श्व बैण्ड ही प्रेषित किया जाता है, परन्तु ग्राही स्टेशन पर वाहक तरंग उत्पन्न करने की सुविधा होती है। यह दर्शाइए कि यदि कोई ऐसी युक्ति उपलब्ध हो जो दो सिग्नलों की गुणा कर सके तो ग्राही स्टेशन पर मॉडुलक सिग्नल की पुनःप्राप्ति सम्भव है।
उत्तर
माना उच्च आवृत्ति वाहक तरंग निम्नलिखित है
c(t)= A_c cos ω_ct
माना आयाम मॉडुलित तरंग का केवल उच्च पार्श्व बैण्ड ही प्रेषित किया जाता है तब संसूचन के बाद अभिग्राही पर उपलब्ध सिग्नल
m(t) = A1 cos (ω_c + ω_m)t
उक्त दोनों की गुणा करने पर,
cm (t) = A_cA₁ cos ω_c t cos (ω_c + ω_m)t
= \(\frac{A_{c} A_{1}}{2}\) [cos (2ω_c + ω_m) t+ cos ω_mt]

इस सिग्नल को निम्न आवृत्ति फिल्टर से पास करने पर यह फिल्टर उच्च आवृत्ति घटक = \(\frac{A_{c} A_{1}}{2}\) cos (2ω_c + ω_m) t को रोक देगा तथा निम्न आवृत्ति घटक \(\frac{A_{c} A_{1}}{2}\) cosω_mt को गुजरने देगा। इस प्रकार हमें मॉडुलक सिग्नल पुनः प्राप्त हो जाएगा।

संचार व्यवस्था बहुविकल्पीय प्रश्नोत्तर

प्रश्न 1.
तीन तरंगें A, B और C जिनकी आवृत्तियाँ क्रमशः 1600 किलोहर्ट्स, 5 मेगाहर्ट्स और 60 मेगाहर्ट्स हैं, एक स्थान से दूसरे स्थान पर भेजी जानी हैं। निम्न में से कौन-सा संचार का सर्वोपयुक्त ढंग है
(a) A को आकाश तरंग के रूप में तथा B और C को व्योम तरंगों के रूप में भेजा जाए
(b) A को भू तरंग, B को व्योम तरंग तथा C को आकाश तरंग के रूप में भेजा जाए
(c) B और C को भू तरंग, तथा A को व्योम तरंग के रूप में भेजा जाए
(d) B को भू तरंग तथा A और C को आकाश तरंग के रूप में भेजा जाए।
उत्तर
(b) A को भू तरंग, B को व्योम तरंग तथा C को आकाश तरंग के रूप में भेजा जाए

प्रश्न 2.
एक 100 मीटर लम्बा एन्टेना 500 मीटर ऊँची इमारत पर लगा है। यह संयोजन 2 तरंगदैर्घ्य की तरंगों के लिए एक संचरण टावर (transmission tower) बन जाएगा जहाँ 2 है
(a) ~ 400 मीटर
(b) ~ 25 मीटर
(c) ~150 मीटर
(d) ~ 2400 मीटर।
उत्तर
(a) ~ 400 मीटर

प्रश्न 3.
3 किलोहर्ट्स आवृत्ति का एक वाक् सिग्नल, 1 मेगाहर्ट्स आवृत्ति के एक वाहक सिग्नल को आयाम मॉडुलीकरण द्वारा मॉडुलित करने के लिए प्रयुक्त किया गया है। पार्श्व बैण्डों की आवृत्तियाँ होंगी
(a) 1.003 मेगाहर्ट्स व 0:997 मेगाहर्ट्स
(b) 3001 किलोहर्ट्स व 2997 किलोह
(c) 1003 किलोहर्ट्स व 1000 किलोहर्ट्स
(d) 1 मेगाहर्ट्स व 0.997 मेगाहर्ट्स।
उत्तर
(a) 1.003 मेगाहर्ट्स व 0:997 मेगाहर्ट्स

प्रश्न 4.
cm आवृत्ति के एक सन्देश सिग्नल को, आयाम मॉडुलित (AM) तरंग प्राप्त करने के लिए, आवृत्ति की एक वाहक तरंग पर आरोपित (superposed) किया गया है। AM तरंग की आवृत्ति होगी
(a) ω_m
(b) ω_c
(c) \(\frac{\omega_{c}+\omega_{m}}{2}\)
(d) \(\frac{\omega_{c}-\omega_{m}}{2}\)
उत्तर
(b) ω_c

प्रश्न 5.
एक पुरुष की वाणी, मॉडुलीकरण व प्रेषण के पश्चात्, ग्राही को महिला की वाणी की भाँति सुनाई देती (प्रतीत होती) …… है। इसका कारण है
(a) अनुपयुक्त मॉडुलन सूचकांक का चुनाव(0 < m < 1 चुना गया)
(b) आवर्धकों के लिए अनुपयुक्त बैण्ड-चौड़ाई का चुनाव
(c) वाहक तरंगों की आवृत्ति का अनुपयुक्त चुनाव
(d) संचरण में ऊर्जा ह्रास।
उत्तर
(b) आवर्धकों के लिए अनुपयुक्त बैण्ड-चौड़ाई का चुनाव

प्रश्न 6.
एक मूल संचार प्रक्रम में होता है
(A) प्रेषक
(B) सूचना स्रोत
(C) सूचना का उपयोग करने वाला
(D) चैनल
(E) ग्राही।
निम्नलिखित में कौन वह सही क्रम प्रदान करता है जिसमें ये एक मूल संचार प्रक्रम में व्यवस्थित होते हैं
(a) ABCDE
(b) BADEC
(c) BDACE
(d) BEADC.
उत्तर
(b) BADEC .

प्रश्न 7.
आयाम मॉडुलित तरंगों के गणितीय व्यंजक की पहचान कीजिए
(a) A_c sin [{ω_c + k₁V_m (t)} t + Φ]
(b) A_c sin {ω_ct + Φ + k₂V_m (t)}
(c) { A_c + k₂V_m (t)} sin (ω_ct+Φ)
(d) A_cV_m(t) sin (ω_ct+Φ).
उत्तर
(c) { A_c + k₂V_m (t)} sin (ω_ct+Φ)

संचार व्यवस्था अति लघु उत्तरीय प्रश्नोत्तर

प्रश्न 1.
निम्नलिखित में किसमें अनुरूप (analog) सिग्नल तथा किसमें अंकीय (digital) सिग्नल उत्पन्न होते हैं?

1. एक कम्पित स्वरित्र द्विभुज
2. सितार के कम्पित तार की सुस्वर ध्वनि
3. प्रकाश स्पन्द
4. NAND गेट (द्वार) का निर्गत।

उत्तर

1. अनुरूप (analog)
2. अनुरूप (analog)
3. अंकीय (digital)
4. अंकीय (digital)।

प्रश्न 2.
क्या व्योम तरंगें, 60 मेगाहर्ट्स आवृत्ति के (टी०वी०) सिग्नलों को प्रेषित करने के लिए उपयुक्त होंगी?
उत्तर
नहीं, क्योंकि 30 मेगाह से अधिक आवृत्ति की तरंगें, आयनमण्डल द्वारा परावर्तित न होकर पारगमित हो जाती हैं।

प्रश्न 3.
दो तरंगें तथा B जिनकी आवृत्तियाँ 2 मेगाहर्ट्स और 3 मेगाहर्ट हैं, एक ही दिशा में, व्योम तरंग के द्वारा संचरित करने के लिए विकीर्णित की जाती हैं। इनमें से कौन-सी आयनमण्डल से पूर्ण आन्तरिक परावर्तन के पूर्व अधिक दूरी तय कर सकती है?
उत्तर
3 मेगाहर्ट्स की अधिक आवृत्ति की तरंग के लिए वायुमण्डल का अपवर्तनांक अधिक होता है। अत: अधिक आवृत्ति की तरंग के लिए अपवर्तन कोण कम होगा अर्थात् यह तरंग अपने मार्ग से कम मुड़ेगी और पूर्ण आन्तरिक परावर्तन से पूर्व अधिक दूरी तय करेगी।

प्रश्न 4.
आयाम मॉडुलन हेतु, 1 मेगाहर्ट्स आवृत्ति की वाहक तरंगों का उत्पादन करने के लिए आवश्यक, एक समस्वरित आवर्धक परिपथ के LC गुणनफल की गणना कीजिए। · हल :
समस्वरित आवर्धक परिपथ के लिए f= \(\frac{1}{2 \pi \sqrt{L C}}\)
\(\begin{aligned} 1 \times 10^{6} &=\frac{1}{2 \pi \sqrt{L C}} \\ \sqrt{L C} &=\frac{1}{2 \pi \times 10^{6}} \end{aligned}\)
\(L C=\frac{1}{4 \pi^{2} \times 10^{12}}\)

प्रश्न 5.
किसी चैनल से संचरण पर, आयाम मॉडुलित (AM) सिग्नल में, आवृत्ति मॉडुलित सिग्नल (FM) से अधिक रव क्यों होता है?
उत्तर
आयाम मॉडुलन में, वाहक तरंगों के तात्कालिक विभव मान में मॉडुलक तरंग विभव के अनुरूप परिवर्तन किया जाता है। सम्प्रेषण में नॉयज सिग्नल (रव) भी जुड़ जाते हैं तथा ग्राही के लिए मॉडुलेटिंग सिग्नल के एक भाग की भाँति ही कार्य करता है। आवृत्ति मॉडुलन में वाहक तरंगों की आवृत्ति में मॉडुलक तरंग विभव के तात्कालिक मान के अनुरूप परिवर्तन किया जाता है। यह प्रक्रम केवल मॉडुलन स्तर पर होता है; सिग्नल के संचरण के समय नहीं। अत: आवृत्ति मॉडुलित सिग्नल में अधिक नॉयज सिग्नल (रव) नहीं होता है।

संचार व्यवस्था आंकिक प्रश्नोत्तर

प्रश्न 1.
एक दूरदर्शन संचरण टावर ऐन्टिना 20 मीटर की ऊँचाई पर है। इससे कितने क्षेत्र में संकेत प्राप्त हो सकेंगेयदिग्राही एन्टिना

1. भूतल पर ही,
2. भूतल से 25 मीटर ऊँचाई पर हो
3. प्रथम स्थिति के सापेक्ष द्वितीय स्थिति में इसमें होने वाली प्रतिशत वृद्धि का परिकलन कीजिए।

हल
1. h = 20 मीटर
संकेत प्राप्त करने वाले क्षेत्र की त्रिज्या

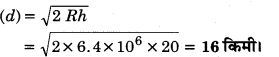
संकेत से आच्छादित क्षेत्रफल (A) = πd²
= 3.14x (16)² किमी²= 3.14×256
= 803.84 किमी²।

2.

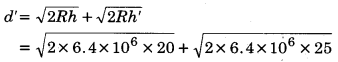
= (16+17.9) किमी  33.9 किमी
संकेत से आच्छादित क्षेत्रफल (A’) = πd²= 3.14 × (33.9)² किमी²
= 3608.52 किमी²

3.  क्षेत्रफल में % वृद्धि = \(\frac { A’ – A }{ A }\)x100%
\(\frac { 3608.52 – 803.84 }{ 803.84 }\) x100 = 348.9%

प्रश्न 2.
आयनमण्डल की एक विशेष परत से परिवर्तित होने वाली व्योम तरंगों की अधिकतम आवृत्ति fmax = 9(Nmax)1/2 पायी जाती है, जहाँ Nmax उस आयनमण्डल की परत में अधिकतम इलेक्ट्रॉन घनत्व है। किसी दिन यह प्रेक्षण किया गया 5 मेगाहर्ट्स से अधिक आवृत्ति के सिग्नल आयनमण्डल को F, परत से परावर्तित होकर प्राप्त नहीं होते हैं जबकि 8 मेगाहर्ट्स से अधिक आवृत्ति के सिग्नल आयनमण्डल को F2 परत से परावर्तन के द्वारा प्राप्त नहीं होते हैं। उस दिन F1 तथा Fपरतों के अधिकतम इलेक्ट्रॉन घनत्व की गणना कीजिए।
हल :

MP Board Class 12th Physics Solutions