MP Board Class 12th Physics Important Questions Chapter 5 Magnetism and Matter
Magnetism and Matter Important Questions
Magnetism and Matter Objective Type Questions
Question 1.
Choose the correct answer of the following:
Question 1.
If a bar magnet is placed with its north pole pointing towards geographical north and south pole pointing towards geographical south, then the neutral point will be:
(a) Situated on the axial line
(b) Situated on the equatorial line
(c) Situated at a place where is neither axial line nor equatorial line
(d) Not formed at all.
Answer:
(b) Situated on the equatorial line
Question 2.
Magnetic moment is which type of physical quantity :
(a) Scalar
(b) Vector
(c) Neutral
(d) None of these.
Answer:
(b) Vector
![]()
Question 3.
If a bar magnet of magnetic moment M is divided in two equal parts, the magnetic moment of each part will be :
(a) 2M
(b) \(\frac {M}{2}\)
(c) M
(d) Zero
Answer:
(b) \(\frac {M}{2}\)
Question 5.
‘weber’ is the unit of:
(a) Magnetic moment
(b) Magnetic induction
(c) Magnetic field
(d) Magnetic flux
Answer:
(d) Magnetic flux
Question 6.
The two magnetic lines of force :
(a) Meet each other at the poles
(b) Meet at the neutral point
(c) Never meet
(d) All the above statements are correct.
Answer:
(c) Never meet
Question 7.
The intensity of magnetic field is defined as :
(a) Magnetic moment per unit volume
(b) Magnetic induction force acting on unit magnetic pole
(c) Number of magnetic lines of force passing per unit area
(d) Number of lines of force passing through unit volume.
Answer:
(c) Number of magnetic lines of force passing per unit area
Question 8.
A magnetic needle is placed in a non – uniform magnetic field. The needle will experience :
(a) A force without any torque
(b) A torque without any force
(c) A force and a torque
(d) Neither a torque nor a force.
Answer:
(c) A force and a torque
Question 9.
The ratio of magnetic field intensities at equal distance in end on position and broadside on position of a small bar magnet is :
(a) 1 : 4
(b) 1 : 2
(c) 1 : 1
(d) 2 : 1.
Answer:
(d) 2 : 1.
Question 10.
A magnetic dipole of magnetic moment M is placed in a magnetic field of intensity B with its axis along the magnetic field. The work done in rotating it by 180° is :
(a) -MB
(b) MB
(c) Zero
(d) +2 MB
Answer:
(d) +2 MB
![]()
Question 11.
If the net magnetic moment of individual atom of a substance is zero, the substance is :
(a) Diamagnetic
(b) Paramagnetic
(c) Ferromagnetic
(d) Non – magnetic.
Answer:
(a) Diamagnetic
Question 12.
Electromagnets are made up of:
(a) Paramagnetic substances
(b) Soft iron
(c) Steel
(d) Diamagnetic substances.
Answer:
(b) Soft iron
Question 13.
At equator the total intensity of earth’s magnetic field is equal to :
(a) V
(b) H
(c) Both
(d) None of these.
Answer:
(b) H
Question 14.
The resultant intensity of earth’s magnetic field at a place is given by :
(a) \(\frac {H}{V}\)
(b) \(\frac {V}{H}\)
(c) \(\sqrt { { H }^{ 2 }+V^{ 2 } }\)
(d) \(\sqrt { { H }^{ 2 }-V^{ 2 } }\)
Answer:
(c) \(\sqrt { { H }^{ 2 }+V^{ 2 } }\)
Question 15.
The value of angle of dip near the magnetic poles is :
(a) 90°
(b) 45°
(c) 30°
(d) Zero.
Answer:
(a) 90°
Question 16.
The south pole of earth’s magnet is :
(a) Near the geographic north pole
(b) Near the geographic south pole
(c) In geographic east
(d) In geographic west.
Answer:
(a) Near the geographic north pole
Question 17.
The angle of dip at equator is :
(a) 90°
(b) 30°
(c) 0°
(d) 45°
Answer:
(c) 0°
Question 18.
In a plane perpendicular to the magnetic meridian, a dip needle :
(a) Will be horizontal
(b) Will be vertical
(c) Will be inclined at angle of dip at that place
(d) Will be inclined at any angle.
Answer:
(b) Will be vertical
Question 2.
Fill in the blanks :
- The SI unit of pole strength is ……………………….
- The direction of magnetic moment of a magnet is always from ………………………. to ………………………. pole.
- The SI unit of magnetic moment is ……………………….
- The magnetic lines of force are ………………………. curve.
- The tangent drawn at any point of a magnetic line of force gives ……………………….
- The magnetic field produced due to a solenoid is same as that produced by a ……………………….
- A magnet is also called a ……………………….
- At same distance, magnetic field intensity in broadside on position is ………………………. the intensity in end on position.
- Nowadays magnetic lines of force are called ……………………….
- At ………………………. point the resultant intensity of magnetic field is zero.
- The temperature at which ferromagnetic substance is converted into paramagnetic substance is known as ……………………….
- The strength of ………………………. magnet can be changed.
- The vertical component of earth’s magnetic field at a place becomes zero where angle of dip is ……………………….
- The angle of dip from equator to poles lies between ………………………..
- ………………………. substances can easily be magnetized.
Answer:
- ampere x metre
- south; north
- ampere x metre2
- Closed
- Direction of magnetic field
- Bar magnet
- Magnetic dipole
- Half
- Magnetic field line
- Neutral
- Curie temperature
- Electro
- Zero
- Zero to 90°
- Ferro – magnetic.
Question 3.
Match the Columns :
I.

Answer:
- (e)
- (a)
- (d)
- (c)
- (b).
II.

Answer:
- (c)
- (d)
- (e)
- (a)
- (b).
III.

Answer:
- (d)
- (a)
- (b)
- (e)
- (c)
Question 4.
Write the answer in one word / sentence :
- Name the elements or parameters of earth’s magnetic field.
- What is the value of angle of dip at poles and equator?
- How is the relative permeability (μr) ofthe material related to susceptibility (xm)?
- Give two examples of diamagnetic substance.
- Name any two paramagnetic substances.
Answer:
1.
- Declination
- Angle of dip
- Horizontal component of earth’s magnetic field
2. Angle of dip at poles is 90° and at equator it is 0°
3. μr = 1 + xm
4. Zinc and Bismuth
5. Aluminium and Manganese.
Magnetism and Matter Very Short Answer Type Questions
Question 1.
Define effective length of a magnet?
Answer:
The distance between two poles of magnet is called its effective length.
Question 2.
What do you mean by intensity of magnetic field? Write its SI unit. Is it scalar or vector?
Answer:
Intensity of magnetic field:
The intensity of field at a point is defined by the force experienced by a unit north pole, placed-at that point.
Its SI unit is tesla or weber metre-2. Magnetic field is a vector.
![]()
Question 3.
Define magnetic lines of force.
Answer:
1st definition:
The magnetic lines of force are the curves in the magnetic field, on which if a unit north pole is placed, then it will follow the imaginary curve drawn.
2nd definition:
“A magnetic line of force is a smooth curve in a magnetic field such that the tangent at any point on it gives the direction of the magnetic field at that point.”
Question 4.
Can two magnetic lines of force intersect?
Or
Magnetic lines of force do not intersect each other, why?
Answer:
No. If the two magnetic lines of force intersect, then there will be two tangents and hence two directions of magnetic field at the point of intersection. This is impossible.
Question 5.
Define magnetic moment. Write its SI unit. Is it a scalar or a vector?
Answer:
The product of pole strength (m) and effective length (2l) of the magnet is called magnetic moment (M).
If m be the pole strength and 2l be the effective length, then
M = m x 2l
SI unit of magnetic moment is weber x metre. It is a vector quantity having a direction from south pole to north pole.
Question 6.
What is a diamagnetic substance?
Answer:
A substance which when placed in a magnetizing field develops very weak magnetization in the opposite direction of the applied field is called diamagnetic substance.
Question 7.
What is paramagnetic substance?
Answer:
A substance which when placed in a magnetizing field develops weak magnetism in the direction of the applied field is called paramagnetic substance.
Question 8.
What is paramagnetism?
Answer:
The atoms or molecules of some materials (e.g., Al, CuCl2) have non – zero magnetic moment. When such a substance is placed in a magnetic field \(\vec { B }\), the individual magnetic dipoles align in the direction of \(\vec { B }\). There is net magnetization in the direction of \(\vec { B }\) and proportional to \(\vec { B }\) This is called paramagnetism.
Question 9.
What are ferromagnetics or ferromagnetic substances?
Answer:
Ferromagnetics are the substances, which when placed in a magnetic field are strongly magnetized in the direction of the magnetizing field. Example Fe. Ni, Co etc.
![]()
Question 10.
Write about the number of electrons in diamagnetic and paramagnetic substances.
Answer:
The number of electrons in diamagnetic substances are in even number and in paramagnetic substances electrons are in odd numbers.
Question 11.
Does the magnetism of paramagnetic salts depend upon temperature? Give reason.
Answer:
Yes, with the increase of temperature its magnetism decreases. When a paramagnetic salt is placed in a magnetic field then on each elementary magnet, a torque acts which tends to bring them in the direction of magnetic field. When the temperature is increased the thermal agitation opposes this tendency, hence the paramagnetism is decreased.
Question 12.
Define magnetic intensity. Give its SI unit.
Answer:
Magnetic intensity is the ability of a magnetizing field to magnetize a material and is defined as the number of ampere turns flowing around unit length of solenoid required to produce magnetic induction B0 inside it.
H = \(\frac { { B }_{ 0 } }{ { \mu }_{ 0 } }\)
SI unit of H is Am-1
Question 13.
Define magnetic permeability. State its SI unit.
Answer:
Magnetic permeability is defined as the ratio of magnetic induction B to the magnetizing field intensity H ie., μ = \(\frac {B}{H}\)
SI unit is TmA-1.
Question 14.
Why the magnetic property increases in paramagnetic substances with cooling?
Answer:
When a paramagnetic substances is kept in an external magnetic field, then on each elementary magnet a torque acts which tries to bring them parallel to the direction of magnetic field. The thermal vibrations opposes it. If the temperature is decreased, then thermal vibrations decreases, hence the magnetic property increases.
Question 15.
Why is diamagnetism independent of temperature?
Answer:
The induced magnetic moment in diamagnetic sample is always opposite to the magnetizing field, no matter what the internal motion of atom is.
Question 16.
What is Curie point?
Answer:
Curie point is the temperature above which a ferromagnetic substance becomes paramagnetic.
Question 17.
At any point on the surface of earth, horizontal component of earth magnetic field and vertical component of it are equal. What will be the angle of dip at that point?
Solution:
According to question H = V
Or BH = Bv
But tanθ = \(\frac { { B }_{ v } }{ { B }_{ H } }\)
Or tanθ = \(\frac { { B }_{ v } }{ { B }_{ v } }\)= 1 =tan45°
θ = 45°
Angle of dip will be 45°.
Question 18.
When a bar magnet is cut into two equal pieces perpendicular to its axis, then what will be its charge in magnetic moments.
Answer:
In this position, magnetic moment of each pieces will be M’ = m’ x 2l
But m’= \(\frac {M}{2}\)
∴ M’ = \(\frac {m}{2}\) x 2l
= \(\frac {M}{2}\)
Therefore magnetic moment will become half of its initial value.
Magnetism and Matter Short Answer Type Questions
Question 1.
Write Coulomb’s law of magnetism and define the unit magnetic pole with its help.
Answer:
Coulomb’s law:
The force of attraction or repulsion between two magnetic poles is directly proportional to the product of pole strength and inversely proportional to the square of the distance between them and acts along the line joining the roles.
Let m1 and m2 be the pole strengths and d be the distance between them, then

Unit pole:
If F = 10-7N, d = 1m and m1=m2 = m, then putting the values in eqn. (2),
we get
10-7 = 10-7\(\frac { { m }^{ 2 } }{ 1 } \) ⇒ m = ±1
Thus, if two similar poles are kept 1m apart in vacuum and repei each other by a force of 10-7N, then the poles are called unit poles.
![]()
Question 2.
What is end – on – position or axial position? Derive an expression for the intensity of field at a point on the axis of a bar magnet. What is the direction of resultant field?
Or
Derive an expression for the intensity of field at a point on the axial position of a bar magnet.
Answer:
End – on – position:
The point where the intensry of the magnetic field is to be found, is on the magnetic axis, then this point is called end – on – position.

Let NS be a bar magnet of pole strength m and effective length 2l. Consider a point P on its axis at a distance d from the centre of the magnet O. Magnetic field at P has to be found out.
Now, the intensity of field at P due to N – pole :
B1 = \(\frac { { \mu }_{ o } }{ 4\pi } .\frac { m }{ N{ P }^{ 2 } }\),(along\(\vec { NP } \))
NP = OP – ON =d – l
∴ B1 =\(\frac { { \mu }_{ o } }{ 4\pi } .\frac { m }{ (d-1)^{ 2 } }\) … (1)
Similarly, the intensity of field at P due to S – pole :
B2 = \(\frac { { \mu }_{ o } }{ 4\pi } .\frac { m }{ S{ P }^{ 2 } } \),(along\(\vec { PS }\))
or ∴ B1 =\(\frac { { \mu }_{ o } }{ 4\pi } .\frac { m }{ (d+1)^{ 2 } }\) … (2)
Since, B1 and B2 are acting in opposite direction and B1 > B2
∴Resultant field B = B1 – B2 (along \(\vec { NP }\))
Putting the values from eqns. (1) and (2),

This is the required expression for the intensity of field on the axis.
Again, if the magnet is small i.e., I << d
By neglecting l.
\(\frac { { \mu }_{ o } }{ 4\pi } .\frac { 2m }{ ({ d }^{ 2 })^{ 2 } }\)
or \(\frac { { \mu }_{ o } }{ 4\pi } .\frac { 2M }{ ({ d })^{ 3 } }\)
In CGS units, B = \(\frac { 2M }{ ({ d })^{ 3 } }\)
The direction of resultant field is along the magnetic axis from south pole to north pole.
Question 3.
What is broad – side – on position or equatorial position? Derive an expression for the intensity at a point on broad – side – on position of a bar magnet. What will be the direction of resultant field?
Or
Determine the force on a unit north pole, kept on the broad-side-on position of a small bar magnet.
Answer:
Broad – side – on position:
When the point where the intensity of the magnetic field has to be found lies on the perpendicularbisector of magnetic axis, i.e., on the neutral axis, then it is called broad – side – on position.
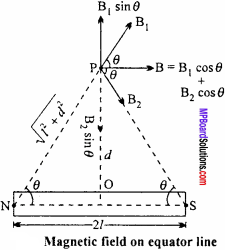
Magnetic field is the force experienced by unit north pole placed at that point.
Hence, B = \(\frac {F}{m}\)
If m = 1, then B = F.
Let NS be a bar magnet of pole strength m and effective length 2l and magnetic moment M = m2l.
Consider a point P at a distance d from the centre O of a magnet on its neutral axis. Let unit north pole be placed at P.
Now, the intensity of field at P, due to N – pole will be :

Resolving B1 and B2 into its components, we have B1, cosθ along NS and B2sinθ⊥ to NS along OP. Also B2 cosθ along NS and B2 sinθ⊥ to NS along PO.
But B1 = B2
⇒ B1 sinθ= B2 sinθ
Since, their directions are opposite and their magnitudes are equal, hence they cancel each other.
The resultant field is therefore
Question 4.
What are magnetic lines of force ? Write down its properties.
Answer:
Magnetic lines of force :
1st definition:
The magnetic lines of force are the curves in the magnetic field, on which if a unit north pole is placed, then it will follow the imaginary curve drawn.
2nd definition:
“A magnetic line of force is a smooth curve in a magnetic field such that the tangent at any point on it gives the direction of the magnetic field at that point.”
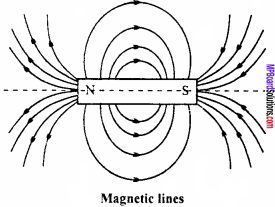
Properties of lines of force :
- They are closed and continuous curves.
- Outside the magnet the direction is from north to south and inside the magnet the direction is from south to north.
- The tangent drawn at any point on the curve gives the direction of the resultant field at that point.
- They do not intersect each other. If two lines of force intersect at a point, then there would be two tangents at that point hence, the resultant force would have two directions; which is not possible, therefore the lines of force do not intersect.
- They are dense near the poles where the magnetic field is strong and get separated where the magnetic field is weak.
- They repel each other in the direction, perpendicular to it, therefore the like poles repel each other.
- They experience tension along the lines of force therefore, unlike poles attract each other.
- They behave just like a stretched elastic string.
Question 5.
Derive an expression for the torque acting on a bar magnet placed in a uniform magnetic field, making angle 0with the field and hence define magnetic moments with its help.
Answer:
Let NS be a bar magnet, placed in a uniform magnetic field of intensity B, making an angle θ with the field. Suppose m be the pole strength and 2l be the effective length, Force acting on each pole will be mB.
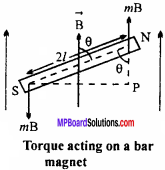
On the N – pole this force will be along the direction of field, whereas on S – pole this will be opposite to the direction of field. As two equal and opposite forces are acting on it along different line of action, hence a couple acts on it which tries to bring the magnet along the direction of magnetic field. This couple is called ‘restoring couple’ or ‘restoring torque’.
Restoring torque is defined as the product of magnitude of any one of the forces and the perpendicular distance between them.
∴ τ = Force x Perpendicular distance
or Torque, τ = mB x SP … (1)
Also, in ANPS, we get sinθ = \(\frac {SP}{NS}\)
or SP = NSsinθ = 2lsinθ
Putting the value of SP in eqn. (1),
τ = mB x 2l sinθ
But m x 2l = M (magnetic moment)
∴ τ = mB sinθ
In vector form :
\(\vec { τ }\) = \(\vec { M }\) x \(\vec { B }\)
and the direction of \(\vec { τ }\) will be perpendicular to the plane containing \(\vec { M }\) and \(\vec { B }\).
Definition of magnetic moment :
As τ = MBsinθ
If the magnet is held perpendicular to the field, then 0= 90° or sinθ = 1 then the torque acting on the magnet will be maximum, if the strength of the applied field is 1 i.e., B = 1,then
τmax = M
Hence, magnetic moment is numerically equal to the maximum torque acting on the bar magnet when it is held perpendicular in a uniform magnetic field of unit intensity.
![]()
Question 6.
Compare to a bar magnet and a current – carrying solenoid.
Answer:
Comparison of a bar magnet and a solenoid :
Bar magnet:
- It attracts magnetic substances.
- When it is suspended freely it rests in the direction of N – S.
- It has two poles.
- Like poles of magnet repel and unlike poles attract.
Solenoid:
- It also attracts magnetic substances.
- It also rests in N – S direction if suspended freely.
- It has also two poles.
- Like poles of solenoid also repel and unlike poles attract.
Question 7.
Explain how does an atom behave as a magnetic dipole. Derive an expression for the magnetic dipole moment of the atom. Also define Bohr magneton.
Or
Deduce the expression for the magnetic dipole moment of an electron orbiting around the central nucleus.
Answer:
Magnetic dipole moment of a revolving electron:
In hydrogen – like atoms, an electron revolves around the nucleus. Its motion is equivalent to a current loop which possesses a magnetic dipole moment = IA. As shown in Fig., consider an electron revolving anticlockwise around a nucleus in an orbit of radius r with speed v and time – period T.
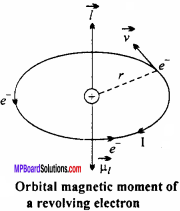
Equivalent current,
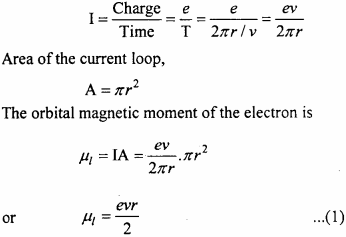
According to right hand thumb rule, the direction of the magnetic dipole moment of the revolving electron will be perpendicular to the plane of its orbit and it the downward direction, as shown in Fig.
Also, the angular momentum of the electron due to its orbital motion is
I = mevr … (2)
The direction of / is normal to the plane of the electron orbit and in the upward direction, as shown in Fig.
Dividing equation. (1) by equation. (2), we get
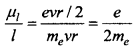
The above ratio is a constant called gyromagnetic ratio. Its value is 8.8 x 1010Ckg-1.
So
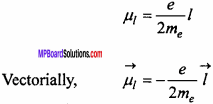
The negative sign shows that the direction of \(\vec { l }\) is opposite to that of \(\vec { { \mu }_{ 1 } }\) According to Bohr’s quantization condition, the angular momentum of an electron in any permissible orbit is,
l = \(\frac { nh }{ 2π }\) , where n =1,2 ,3, ………….
∴ µ1 = n(\(\frac { eh }{ 4\pi { m }_{ e } }\))
This equation gives orbital magnetic moment of an electron revolving in nth orbit.
Bohr magneton:
It is defined as the magnetic moment associated with an electron due to its orbital motion in the first orbit of hydrogen atom. It is the minimum value of µ1, which can be obtained by putting n = 1 in the above equation. Thus Bohr magneton is given by
µB= (µ1)min = \(\frac { eh }{ 4\pi { m }_{ e } }\) = 9.27 x 10-24Am2.
Question 8.
Derive an expression for work done in rotating a bar magnet in uniform magnetic field through 8 angle.
Answer:
Let a bar magnet of effective length 2l and of magnetic moment M be kept in uniform magnetic field B. When a bar magnet is rotated through some angle in the magnetic field then some work has to be done against moment of restoring couple.
If magnet is rotated through dQ angle then work done, dW = τ dθ,
(where τ is moment of restoring couple)
or dW = MB sinθ dθ … (1)
When magnet is rotated from θ1 to θ2, then work done is given by :
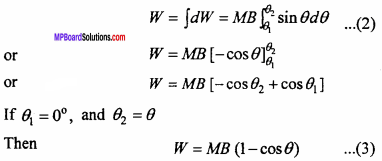
This is the required expression.
Question 9.
Establish the expression for potential energy of a bar magnet placed in a uniform magnetic field.
Answer:
The potential energy of the bar magnet in any orientation is the work done by the external agent to turn the dipole from its zero position (θ = 90°) to that orientation (θ = θ°)
dW = MB sinθ dθ … (1)
Amount of work done to rotate the bar magnet from zero position (θ = π/2) to an arbitrary position (θ = θ) will be obtained by integrating equation (1) under proper limit.

Question 10.
Define the magnetic elements of earth’s magnetic field at a place.
Or
Establish relation between element of earth’s magnetic field?
Answer:
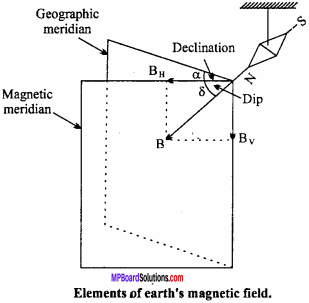
Elements of earth’s magnetic field:
The earth’s magnetic field at a place can be completely described by three parameters which are called elements of earth’s magnetic field. They are declination, dip and horizontal component of earth’s magnetic field.
1. Magnetic declination:
The angle between the geographical meridian and the magnetic meridian at a place is called the magnetic declination (α) at that place, Or, it is the angle which a compass needle (free to swing in a horizontal planb) makes with the geographic north – south direction.
2. Angle of dip or magnetic inclination:
The angle made by the earth’s total magnetic field \(\vec { B }\) with the horizontal direction in the magnetic meridian is called angle of dip (δ) at any place. Or, it is the angle which a dip needle (free to swing in the plane of the magnetic meridian) makes with the horizontal.
At the magnetic equator, the dip needle rests horizontally so that the angle of dip is zero at the magnetic equator. The dip needle rests vertically at the magnetic poles so that the angle of dip is 90° at the magnetic poles. At all other places, the dip angle lies between 0° and 90°.
3. Horizontal component of earth’s magnetic field:
It is the component of the earth’s total magnetic field \(\vec { B }\) in the horizontal direction in the magnetic meridian. If δ is the angle of dip at any place, then the horizontal component of earth’s field \(\vec { B }\) at that place is given by
BH = Bcosδ
At the magnetic equator,
δ = 0°,BH = Bcos0°= B
At the magnetic poles,
δ = 90°,BH =5cos90°= 0
Thus the value of BH is different at different places on the surface of the earth.
![]()
Question 11.
Prove tanδ = \(\frac { { B }_{ v } }{ { B }_{ H } }\) and B = \(\sqrt { { B }_{ H }^{ 2 }+{ B }_{ v }^{ 2 } }\) where symbol have there usual meaning.
Answer:
Relations between elements of earth’s magnetic field:
Fig. shows the three elements of earth’s magnetic field. If 8 is the angle of dip at any place, then the horizontal and vertical components of earth’s magnetic field B at that place will be
BH = Bcosδ .. (1)
and Bv = Bsinδ
\(\frac { { B }_{ v } }{ { B }_{ H } }\) = \(\frac { Bsinδ }{ Bcosδ}\)
\(\frac { { B }_{ v } }{ { B }_{ H } }\) =tanδ .. (2)
Also
B2H + B2v = B2(cos2δ + sin2δ) = B2
or B = \(\sqrt { { B }_{ H }^{ 2 }+{ B }_{ v }^{ 2 } }\) .. (3)
Equations (1), (2) and (3) are the different relations between the elements of earth’s magnetic field.
Question 12.
Compare the magnetic properties of soft iron and steel.
Answer:
Comparison of magnetic properties of soft iron and steel:
Soft iron:
- In soft iron, greater magnetism can be produced, than steel. Its magnetic nature is greater than steel.
- Soft iron does not retain magnetism for longer time. Its retaintivity is less.
- The magnetization and demagnetization of soft iron are easy.
- Temporary magnets are made by soft iron.
Steel:
- In steel, less magnetism can be produced than soft iron, its magnetic nature is less than soft iron.
- Steel retains magnetism for longer time. Its retaintivity is greater than soft iron.
- The magnetization and demagnetization of steel are difficult.
- Permanent magnets are made by soft steels.
Magnetism and Matter Long Answer Type Questions
Question 1.
Answer the following regarding terrestrial magnetism quantities :
- Three quantities are required to express a vector completely write the name of that there independent quantity.
- At which place of south India the angle of dip in 18° will you expect more value of angle of dip at britain ?
- If you draw lines of forces at Melbourne city of Austrilia. This lines of forces will go inside the earth or outside.
- The magnetic needle which is free to revolve in vertical plane. If it is kept at geographical north or south pole then in which direction it will revolve?
Answer:
1.
- Angle of declination
- Angle of dip
- Horizontal component of Earth magnetic field.
2. Britain is near magnetic pole of earth, therefore angle of dip at Britain is more than the angle of dip at south India (approx. 70°).
3. The magnetic lines of force at Melbourne city of Austrilia will go outside.
4. Geographical North pole or South pole is just situated vertically to the direction of earth magnetic field. Therefore the magnetic needle will be independent to revolve in vertical plane
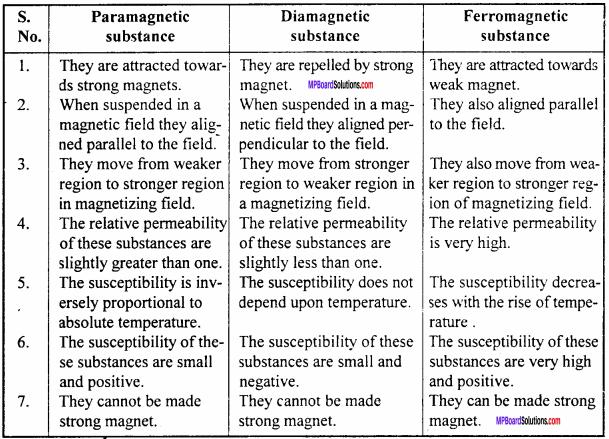
Question 2.
Compare the magnetic properties of paramagnetic substance and ferromagnetic substance on any three points.
Answer:
Comparison :
Question 3.
What do you mean by magnetic field intensity. Derive an expression for magnetic field due to a bar magnet in general position. How is this formula used to find magnetic field in
- Axial position
- Equatorial position.
Answer:
The force experienced by unit north pole at any point in the magnetic field is known as magnetic field intensity. NS is a bar magnet of magnetic moment \(\vec { M }\), we have to find out magnetic field intensity at P, which is situated at θangle from axis of magnet.
Now, we divide M into two components
- Mcosθ
- Msinθ
For Mcosθ point ‘P’ lies in axial position, therefore magnetic field at P due to M cos G component is :
B1 = \(\frac { { \mu }_{ 0 } }{ 4\pi } \frac { 2Msin\theta }{ { d }^{ 3 } }\) … (1)
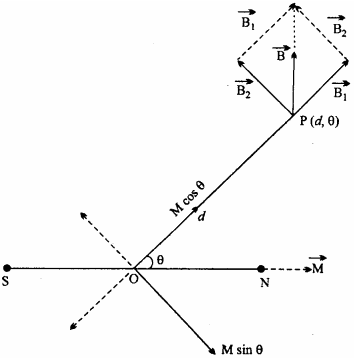
For M sinθ point P lies on equatorial position :
B2 = \(\frac { { \mu }_{ 0 } }{ 4\pi } \frac { Msin\theta }{ { d }^{ 3 } }\) … (2)
∵ B1is perpendicular to B2 , the resultant of B1 and B2 is given by :
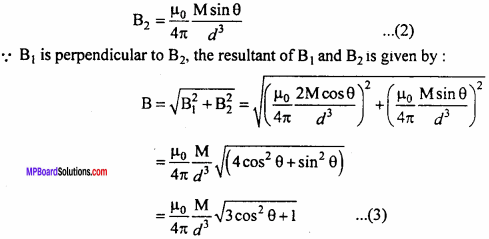
This is the required expression.
(i) For axial position θ = 0° => cos 0°= 1
∴From eqn. (3),
B = \(\frac { { \mu }_{ 0 } }{ 4\pi } \frac { 2M }{ { d }^{ 3 } } \)
From equatorial position θ = 90° ⇒ cos90° = 0
B = \(\frac { { \mu }_{ 0 } }{ 4\pi } \frac { M }{ { d }^{ 3 } } \)
Magnetism and Matter Numerical Questions
Question 1.
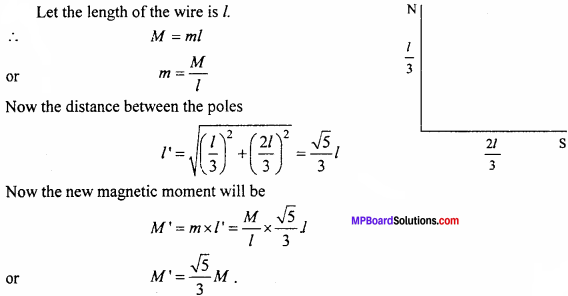
Magnetic wire of magnetic moment ‘M’ is bent in the shape of L, at one third of its length. What will be the new magnetic moment.
Solution:
Question 2.
The length of magnetic wire is L and its magnetic moment is M. If it is bent in the form of semi – circle then what will be its new magnetic moment?
Solution:
Initial magnetic moment of magnetic wire M = mL
If it is bent in the form of semi – circle then
L = πr ⇒ r = \(\frac {L}{π}\)
New magnetic moment M’ = m x 2r
M’ = m x \(\frac {2L}{π}\)
or M’ = \(\frac {2M}{π}\)
Question 3.
The distance between two magnetic poles of pole strengths ‘m’ and ‘4m’ is 3m. Find the distance of point in between them at which magnetic field intensity is zero.
Solution:

Question 4.
If the pole strength of each pole of two similar magnetic poles is made two times and distance between them becomes half of its initial value then how will magnetic force acting between them change?
Solution:

Force becomes 16 times its initial value.
Question 5.
Obtain the earth’s magnetization. Assume that the earth’s field can be approximated by a giant bar magnet of magnetic moment 8.0 x 1022Am2. The earth’s radius is 6400 km. [NCERT]
Solution:
Here magnetic moment m = 8.0 x 1022 Am2
Radius of the Earth R = 6400 km = 6.4 x 106m

Question 6.
A solenoid has a core of a material with relative permeability 400. The windings of the solenoid are insulated from the core and carry a current of 2A. If the number of turns is 1000 per metre, calculate (a) H, (b) M, (c) B and (d) the magnetizing current IM. [NCERT]
Solution:
Here n = 1000 tums/m, I = 2A, μr = 400
1. H = nI = 1000 x 2 = 2x 103 Am-1
2. M = xmH = (μr -1)H
= (400 – 1) x 2 x 103 ≈ 8 x 105Am-1
3. B = μH = μrμ0H
= 400 x 4π x 10-7 x 2 x 103 T = 1.0T .
4. As M = nIM
∴ IM = \(\frac {M}{n}\)
= \(\frac { 8\times { 10 }^{ 5 } }{ 1000 }\)
= 8 x 102 A.
![]()
Question 7.
A short bar magnet placed with its axis at 30° experiences a torque of 0.016 Nm in an external field of 800G
- What is the magnetic moment of the magnet?
- What is the work done by an external force in moving it from its most stable to most unstable position?
- What is the work done by the force due to the external magnetic field in the process mentioned in part (b)?
- The bar magnet is replaced by a solenoid of cross – sectional area 2 x 10-4 and 1000 turns, but the same magnetic moment Determine the current flowing through the solenoid. [NCERT]
Solution:
1. Here θ = 30°, B = 800G = 800 x 10-4T, τ = 0.016Nm
Magnetic moment,
m = \(\frac {τ }{B sinθ}\) =\(\frac { 0.016 }{ 800\times { 10 }^{ -4 }\times sin30° }\)
= 0.40 Am2.
2. For most stable position θ = 0°and for most unstable position θ = 180°. So the required work done by the external force,
W = mB (cos 180°- cos0°) = 2mB
= 2 x 0.40 x 800 x 10-4
=0.064J
3. Here the displacement and the torque due to the magnetic field are in opposition. So the work done by the magnetic fied due to the external magnetic field is,
WB = 0.064J
4. Here A =2 x 10-4m2, N = 1000
Magnetic moment of solenoid,
ms = m = 0.40 Am2
But ms = NIA.
∴ current, I = \(\frac { { m }_{ s } }{ NA }\) = \(\frac { 0.40 }{ 1000\times 2\times { 10 }^{ -4 } }\)
![]()
Question 8.
In the magnetic meridian of a certain place, the horizontal component of the earth’s magnetic field is 0.26G and the dip angle is 60°. What is the magnetic field of the Earth in this location?
Solution:
Here BH= 0.26G, δ = 60°
As BH = Bcosδ
∴ B = \(\frac { { B }_{ H } }{ cos\delta }\)
= \(\frac {0.26}{cos60°}\)
= \(\frac {0.26}{0.5}\)
= 0.52G
Question 9.
What is the magnitude of the equatorial and axial fields due to a bar magnet of length 5 cm at a distance of 50 cm from its mid – point? The magnetic moment of the bar magnet is 0.40 Am2. [NCERT]
Sol. Here m = 0.40 Am2
r = 50 cm = 0-50 m, 21 = 5-0 cm
Clearly, the magnet is a short magnet (l<<r)
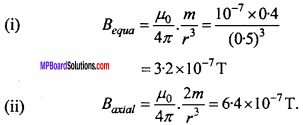
Question 10.
A planar loop of irregular shape encloses an area of 7.5 x 10-4 m2 and carries a current of 12 A. The sense of flow of current appears to be clockwise to an observer. What is the magnitude and direction of the magnetic moment vector associated with the current loop? [NCERT]
Solution:
Here A = 7.5 x 10-4m2, l = 12A
Magnetic moment associated with the loop is
m = IA = 12 x 7.510-4 = 9.0 x 10-3 JT-1
Applying right hand rule, the direction of magnetic moment is along the normal to the plane of the loop away from the observer.