MP Board Class 12th Physics Important Questions Chapter 4 गतिमान आवेश और चुम्बकत्व

Students get through the MP Board Class 12th Physics Important Questions Chapter 4 गतिमान आवेश और चुम्बकत्व which are most likely to be asked in the exam.

MP Board Class 12th Physics Important Questions Chapter 4 गतिमान आवेश और चुम्बकत्व

अति लघु उत्तरीय प्रश्न

प्रश्न 1.
विद्युत् धारा के चुम्बकीय प्रभाव की खोज किसने की थी?
उत्तर-
ओर्टेड ने।

प्रश्न 2.
एक गतिमान आवेश कौन सा क्षेत्र उत्पन्न करता है ?
उत्तर-
विद्युत् एवं चुम्बकीय क्षेत्र दोनों।।

प्रश्न 3.
दिए गए चित्र में धारावाही वृत्ताकार लूप प्रदर्शित किया गया है, जिसमें धारा ‘I’ प्रवाहित हो रही है। चुम्बकीय क्षेत्र की दिशा क्या होगी?

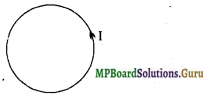
उत्तर-
कुंडली के तल के लम्बवत ऊपर की ओर।

प्रश्न 4.
टोरॉइड (Toroid) में चुम्बकीय क्षेत्र रेखाएँ पूर्णतः टोरॉइड के क्रोड के अंदर सीमित रहती है, क्यों?
उत्तर-
क्योंकि टोरॉइड में स्वतंत्र सिरे नहीं होते।

प्रश्न 5.
एकसमान चुम्बकीय क्षेत्र \(\overrightarrow{\boldsymbol{B}}\) में, \(\overrightarrow{\boldsymbol{v}}\) वेग से गतिमान आवेश q पर लगने वाले बल की दिशा क्या होगी?
उत्तर-
आवेश q पर लगने वाला बल \(\overrightarrow{\mathrm{F}}\) = q\((\vec{v} \times \overrightarrow{\mathrm{B}})\) होगा। यह बल \(\overrightarrow{\boldsymbol{v}}\) एवं \(\overrightarrow{\boldsymbol{B}}\) दोनों के लम्बवत् होगा।

प्रश्न 6.
चल कुंडल धारामापी में चुम्बकीय क्षेत्र की प्रकृति क्या होती है ?
उत्तर-
चुम्बकीय क्षेत्र त्रिज्यीय (Radial) होता है।

प्रश्न 7.
A क्षेत्रफल वाले वृत्ताकार लूप, जिसमें ‘I’ धारा प्रवाहित हो रही है, के चुम्बकीय आघूर्ण हेतु व्यंजक सदिश रूप में लिखिए।
उत्तर-
\(\vec{M}\) =I.\(\vec{A}\) .

प्रश्न 8.
एकसमान चुम्बकीय क्षेत्र में गतिमान आवेश पर लगने वाला बल कब अधिकतम होगा?
उत्तर-
जब आवेश चुम्बकीय क्षेत्र के लम्बवत् गति करता है।

प्रश्न 9.
धारावाही दो समानांतर तार एक-दूसरे को कब आकर्षित करते हैं ?
उत्तर-
जब दोनों तारों में धारा एक ही दिशा में प्रवाहित होती है।

प्रश्न 10.
धारावाही दो समानांतर तार एक-दूसरे को कब प्रतिकर्षित करते हैं ?
उत्तर-
जब दोनों तारों में धारा विपरीत दिशा में प्रवाहित होती है।

लघु उत्तरीय प्रश्न

प्रश्न 1.
विद्युत् धारा के चुम्बकीय प्रभाव से आप क्या समझते हैं ? ..
उत्तर-
किसी चालक में विद्युत् धारा प्रवाहित करने पर चालक के चारों ओर चुम्बकीय क्षेत्र उत्पन्न हो जाता है। इस घटना को विद्युत् धारा का चुम्बकीय प्रभाव कहते हैं।

प्रश्न 2.
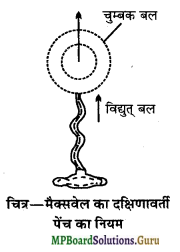
मैक्सवेल का दक्षिणावर्ती पेंच का नियम लिखिए।
उत्तर-
दक्षिणावर्ती कॉर्क पेंच को इस तरह घुमाया जाये कि वह विद्युत् धारा की दिशा में आगे बढ़े तो ऐसा करने के लिए हाथ के अंगूठे को जिस दिशा में घुमाना पड़ता है, वही बल रेखाओं की दिशा होगी। यही मैक्सवेल का दक्षिणावर्ती पेंच का नियम है।

प्रश्न 3.
धारा का व्यावहारिक मात्रक क्या है ? इसे परिभाषित कीजिए।
उत्तर-
धारा का व्यावहारिक मात्रक ऐम्पियर है। एक ऐम्पियर वह विद्यत धारा है जो 1 मीटर त्रिज्या के 1 मीटर चित्र-मैक्सवेल का दक्षिणावर्ती पेंच का नियम लम्बाई के चाप में प्रवाहित करने पर चाप के केन्द्र पर 10^-7 वबर/मीटर² का चुम्बकीय क्षेत्र उत्पन्न कर दे।

प्रश्न 4.
चुम्बकीय क्षेत्र में विद्युत्वाही चालक पर लगने वाले बल के लिए व्यंजक लिखिए तथा संकेताक्षरों के अर्थ समझाइये।
उत्तर-चुम्बकीय क्षेत्र में विद्युत्वाही चालक पर लगने वाला बल
F = I/Bsinθ
जहाँ I = विद्युत् धारा, I = चालक की लम्बाई, B = चुम्बकीय क्षेत्र की तीव्रता, θ = चालक और चुम्बकीय क्षेत्र की दिशा के बीच का कोण।

प्रश्न 5.
SI पद्धति में चुम्बकीय क्षेत्र की तीव्रता का मात्रक लिखिए एवं उसे परिभाषित कीजिए।
उत्तर-
SI पद्धति में चुम्बकीय क्षेत्र की तीव्रता का मात्रक न्यूटन/ऐम्पियर × मीटर है।
सूत्र F = I/Bsinθ में यदि 1 = ऐम्पियर, 1 = 1 मीटर, F= 1 न्यूटन तथा sinθ = 1 अर्थात् θ = 90° हो तो B = 1 न्यूटन/ऐम्पियर × मीटर।
यदि चुम्बकीय क्षेत्र के लम्बवत् स्थित 1 मीटर लम्बे चालक तार में 1 ऐम्पियर की धारा प्रवाहित करने पर उस पर 1 न्यूटन का बल लगे तो उस चुम्बकीय क्षेत्र की तीव्रता । न्यूटन प्रति ऐम्पियर प्रति मीटर होती है।

प्रश्न 6.
चल कुण्डली धारामापी की कुण्डली के मध्य नर्म लोहे का क्रोड क्यों रखते हैं ?
उत्तर-
इसके कारण निम्नलिखित हैं

• नर्म लोहे की चुम्बकशीलता अधिक होती है। अतः इसमें से होकर अधिक-से-अधिक बल-रेखाएँ गुजरने का प्रयास करती हैं जिससे चुम्बकीय क्षेत्र की तीव्रता बढ़ जाती है।
• क्षेत्र को त्रिज्यीय होने में सहायता मिलती है, जिससे कुण्डली का तल सदैव बल-रेखाओं के समान्तर होता है।

प्रश्न 7.
धारामापियों में चुम्बक के ध्रुव अवतल क्यों बनाए जाते हैं ?
उत्तर-
जिससे कि कुण्डली का कार्य करने वाला चुम्बकीय क्षेत्र त्रिज्यीय हो जाये और कुण्डली का तल सदैव बल-रेखाओं के समान्तर हो।

प्रश्न 8.
क्या होगा यदि वोल्टमीटर को परिपथ के श्रेणी क्रम में जोड़ दें?
उत्तर-
यदि वोल्टमीटर को परिपथ के श्रेणी क्रम में जोड़ दें तो परिपथ में धारा का मान बहुत कम होगा क्योंकि वोल्टमीटर का प्रतिरोध बहुत अधिक होता है।

प्रश्न 9.
यदि अमीटर को किसी परिपथ में समान्तर क्रम में जोड़ दिया जाये तो क्या होगा?
उत्तर-
यदि अमीटर को किसी परिपथ में समान्तर क्रम में जोड़ दिया जाये तो प्रतिरोध कम होने के कारण उसमें अत्यधिक धारा बहेगी जिससे उसका संकेतक अत्यधिक विक्षेप के कारण टूट सकता है या कुण्डली जल सकती है।

प्रश्न 10.
किसी विद्युत् परिपथ में अमीटर को श्रेणीक्रम में क्यों जोड़ते हैं ?
उत्तर-
अमीटर को श्रेणीक्रम में इसलिए जोड़ते हैं ताकि सम्पूर्ण विद्युत् धारा उसमें से होकर प्रवाहित हो सके। इसके अतिरिक्त अमीटर का प्रतिरोध कम होता है। अतः उसे श्रेणीक्रम में जोड़ने पर मुख्य धारा के मान में कोई परिवर्तन नहीं होता।

प्रश्न 11.
एक आदर्श वोल्टमीटर का प्रतिरोध कितना होना चाहिए और क्यों?
उत्तर-
एक आदर्श वोल्टमीटर का प्रतिरोध अनन्त होना चाहिए। वोल्टमीटर को विद्युत् परिपथ में समान्तर क्रम में जोड़ा जाता है। यदि वोल्टमीटर का प्रतिरोध अत्यधिक है तो उसमें से होकर नगण्य धारा प्रवाहित होगी। अतः मुख्य परिपथ में प्रवाहित होने वाली धारा में कोई उल्लेखनीय परिवर्तन नहीं होगा।

प्रश्न 12.
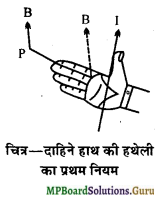
दाहिने हाथ की हथेली का नियम नं. 1 क्या है ? लिखिए एवं उपयोग बताइये।
अथवा
धारावाही चालक में उत्पन्न चुम्बकीय क्षेत्र की दिशा ज्ञात करने हेतु दायें हाथ की हथेली का नियम लिखिए एवं चित्र द्वारा दर्शाइये।
उत्तर’-
अपने दाहिने हाथ की हथेली को इस प्रकार फैलाओ कि उँगलियाँ अँगूठे के लम्बवत् हों। अब यदि अँगूठा चालक में बहने वाली धारा की दिशा में हो तथा उँगलियाँ उस बिन्दु की ओर संकेत करें जिस बिन्दु पर चुम्बकीय क्षेत्र ज्ञात करना है, तो चुम्बकीयमा क्षेत्र हथेली के लम्बवत् बाहर की ओर होगा।
उपयोग-इस नियम की सहायता से धारावाही चालक के चित्र-दाहिने हाथ की हथेली कारण किसी बिन्दु पर चुम्बकीय क्षेत्र की तीव्रता की दिशा ज्ञात हो का प्रथम नियम जाती है।

प्रश्न 13.
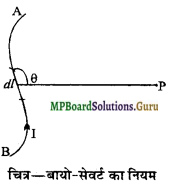
बायो-सेवर्ट के नियम की व्याख्या कीजिए।
अथवा
बायो-सेवर्ट के नियम का व्यंजक ज्ञात कीजिए।
अथवा
बायो-सेवर्ट का नियम लिखिए तथा इसकी सहायता से विद्युत् धारा के मात्रक को परिभाषित कीजिए।
उत्तर-
मानलो AB एक चालक है, जिसमें I विद्युत् धारा प्रवाहित हो रही है। तब इस धारावाही चालक के एक अल्पांश द्वारा उत्पन्न चुम्बकीय क्षेत्र के किसी बिन्दु पर चुम्बकीय क्षेत्र की तीव्रता dB
(i) चालक में बहने वाली धारा I के अनुक्रमानुपाती होती है अर्थात्
dB ∝I
(ii) चालक के उस अल्पांश की लम्बाई dl के अनुक्रमानुपाती होती है अर्थात्
dB ∝dl
(iii) अल्पांश की लम्बाई और अल्पांश को बिन्दु P से मिलाने वाली रेखा के बीच बनने वाले कोण θ की ज्या (sine) के अनुक्रमानुपाती होती है अर्थात्
चित्र-बायो-सेवर्ट का नियम dB∝sinθ
(iv) अल्पांश से बिन्दु P के बीच की दूरी r के वर्ग के व्युत्क्रमानुपाती होती है अर्थात्
dB ∝ \(\frac{1}{r^{2}}\)

उपर्युक्त चारों को मिलाकर लिखने पर,
dB ∝ \(\frac{\text { I. } d l \cdot \sin \theta}{r^{2}}\)
dB = K.\(\frac{\text { I. } d l \cdot \sin \theta}{r^{2}}\)
जहाँ, K एक आनुपातिक नियतांक है, जिसका मान मापन की पद्धति पर निर्भर करता है।
M.K.S. पद्धति में, K = \(\frac{\mu_{0}}{4 \pi}\) = 10^-7 न्यूटन / ऐम्पियर²
∴ dB = 10^-7 \(\frac{\text { I. } d l \cdot \sin \theta}{r^{2}}\)
उपर्युक्त सूत्र में यदि dl = 1 मीटर, r = 1 मीटर, sin θ = 1 अर्थात् θ = 90° तथा dB = 10^-7वेबर / मीटर² हो, तो I = 1 ऐम्पियर।
अतः 1 ऐम्पियर वह विद्युत् धारा है, जो 1 मीटर त्रिज्या के 1 मीटर लम्बाई के चाप में प्रवाहित करने पर चाप के केन्द्र पर 10^-7 वेबर/मीटर का चुम्बकीय क्षेत्र उत्पन्न कर दे।

प्रश्न 14.
किसी टोरोइड (Toroid) के कारण चुम्बकीय क्षेत्र की तीव्रता का व्यंजक ज्ञात कीजिये।
उत्तर-
एक परिनालिका जो कि एक बंद वलय बनाती है टोरोइड कहलाती है।
चित्र (a) में एक टोरोइड प्रदर्शित है एवं चित्र
(b) में इसका परिच्छेद प्रदर्शित है। टोरोइड के अंदर प्रत्येक बिन्दु पर चुम्बकीय क्षेत्र B नियत रहता है जबकि टोरोइड के अंदर बिन्दु P एवं इसके बाहर बिन्दु Q पर चुम्बकीय क्षेत्र शून्य होता है।

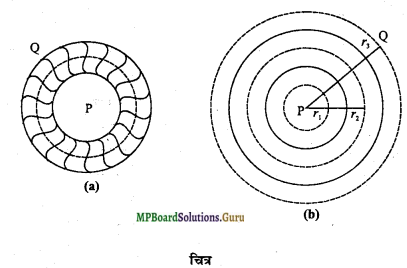
(i) टोरोइड के अंदर के रिक्त स्थान जहाँ बिन्दु P स्थित है पर चुम्बकीय क्षेत्र-
माना लूप 1 जिसकी त्रिज्या । है के किसी बिन्दु पर चुम्बकीय क्षेत्र की तीव्रता B, है।
लूप की लम्बाई (परिधि) = 2.πr₁
इस लूप के लिये I = 0 क्योंकि इस लूप में कोई भी विद्युत् धारा नहीं है। ऐम्पियर के परिपथीय नियम से,
B₁L₁ = µ₀I,
या B₁ .2πr₁ = µ₀ × 0
∴ B = 0
अतः इस लूप में स्थित किसी बिन्दु पर चुम्बकीय क्षेत्र की तीव्रता शून्य होगी।
(ii) टोरोइड के अंदर के किसी बिन्दु पर चुम्बकीय क्षेत्र की तीव्रता-माना r₂ त्रिज्या के लूप 2 में स्थित किसी बिन्दु पर चुम्बकीय क्षेत्र की तीव्रता B है।
इस लूप की लम्बाई L₂ = 2 πr
माना टोरोइड में कुल फेरों की संख्या N है तथा इससे धारा I प्रवाहित हो रही है अत: टोरोइड से संबद्ध कुल विद्युत् धारा
= NI
ऐम्पियर के परिपथीय नियम से,
B.2πr = µ₀NI या B = \(\frac{\mu_{0} \mathrm{NI}}{2 \pi r}\)
किन्तु N = 2 πrn (जहाँ n प्रति एकांक लम्बाई फेरों की संख्या है।)
∴ B = \(\frac{\mu_{0} 2 \pi r n I}{2 \pi r}\) या B =µ₀nI.
(iii) टोरोइड के बाहर के क्षेत्र के किसी बिन्दु पर चुम्बकीय क्षेत्र की तीव्रता-चूँकि इस लूप से सम्बद्ध विद्युत् धारा शून्य है। अतः I = 0.
∴B₃ = 0.

प्रश्न 15.
बायो-सेवर्ट के नियम एवं कूलॉम के व्युत्क्रम वर्ग नियम के बीच कोई चार समानताएँ लिखिये।
उत्तर-
बायो सेवर्ट नियम एवं कूलॉम के व्युत्क्रम वर्ग नियम के बीच समानताएँ निम्नांकित हैं

• दोनों नियम व्युत्क्रम वर्ग नियम का पालन करते हैं।
• दोनों नियम से दिये जाने वाले क्षेत्र दीर्घ परास क्षेत्र हैं।
• दोनों नियमों से दिये गये क्षेत्रों के लिये अध्यारोपण का सिद्धान्त लागू होता है।
• दोनों ही क्षेत्र चालक के चारों ओर के माध्यम से प्रभावित होते हैं।

प्रश्न 16.
ऐम्पियर का परिपथीय नियम लिखिये तथा इसे सिद्ध कीजिए।
उत्तर-किसी बन्द वक्र के लिये चुम्बकीय क्षेत्र \(\overrightarrow{\mathbf{B}}\) का रेखीय समाकलन, बन्द वक्र द्वारा धेरै गये क्षेत्रफल में उपस्थित कुल धारा I का µ₀गुना होता है। अर्थात्
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}\) = µ₀I …………………. (1)
जहाँ \(\oint\) किसी बन्द वक्र के अनुदिश रेखीय समाकलन प्रदर्शित करता है। µ₀ निर्वात् की चुम्बकशीलता (Permeability of free space) कहलाता है।

उत्तपत्ति (Proof)-असीमित लम्बाई के एक ऋजुरेखीय चालक XY की कल्पना करो जिसमें I धारा प्रवाहित हो रही है।
इस चालक के चारों ओर चुम्बकीय बल रेखाएँ संकेन्द्रीय वृत्तों (Concentric circles) के रूप में होंगी जो चालक के लम्बवत् तल में स्थित होंगी।
तब चालक से r दूरी पर स्थित किसी बिन्दु P पर चुम्बकीय क्षेत्र की तीव्रता B= \(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 \mathrm{I}}{r}\) – \( \frac{\mu_{0} I}{2 \pi r}\) ………………….. (1)

चुम्बकीय बल रेखा के किसी बिन्दु पर चुम्बकीय क्षेत्र की तीव्रता \(\overrightarrow{\mathbf{B}}\) उस बिन्दु पर स्पर्श रेखा की दिशा में होती है।
r त्रिज्या के वृत्त के बिन्दु P पर अल्पांश \(\overrightarrow{d l}\) की कल्पना करो । तब \(\overrightarrow{\mathbf{B}}\) और \(\overrightarrow{d l}\) की दिशा एकसमान होगी। अर्थात् उनके बीच का कोण 0° होगा।

अब r त्रिज्या के वृत्त के चारों ओर क्षेत्र \(\overrightarrow{\mathbf{B}}\) का रेखीय समाकलन
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}\) = \(\oint \mathrm{B} \cdot dlcos0°\) = \(\oint \mathrm{B} \cdot d l\)
=\(\oint \frac{\mu_{0} I}{2 \pi r}\)dl = \(\frac{\mu_{0} \mathrm{I}}{2 \pi r}\) 2πr
किन्तु \(\oint\) dl = 2πr=r त्रिज्या के वृत्त की परिधि
अतः \(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}\) = \(\frac{\mu_{0} \mathrm{I}}{2 \pi r} \) 2πr
या
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}\) = µ₀I

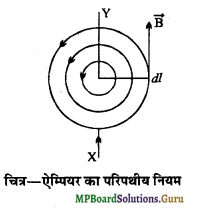
यही ऐम्पियर का परिपथीय नियम है।
यह नियम केवल ऋजुरेखीय चालक या वृत्तीय पथ के लिये सत्य हो ऐसा नहीं है बल्कि सभी प्रकार के बंद वक्रीय पथों, सभी धारा समूहों तथा सभी प्रकार के चुम्बकीय क्षेत्रों के लिये सत्य है।
यही अभीष्ट व्यंजक है।

प्रश्न 17.
ऐम्पियर का परिपथीय नियम लिखिये तथा इस नियम की सहायता से लम्बे ऋजुरेखीय धारावाही चालक तार के समीप चुम्बकीय क्षेत्र की तीव्रता के लिये व्यंजक ज्ञात कीजिये।
उत्तर-
ऐम्पियर का परिपथीय नियम-उपर्युक्त प्रश्न देखिये। चित्र के अनुसार मानलो किसी लम्बे ऋजुरेखीय चालक MN में प्रवाहित धारा I है । इसके कारण चालक के अक्ष से दूरी पर स्थित किसी बिन्दु P पर उत्पन्न चुम्बकीय क्षेत्र की तीव्रता का व्यंजक प्राप्त करना है।

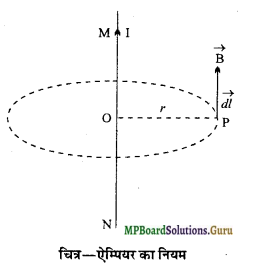
चालक में प्रवाहित धारा I के कारण उत्पन्न बल रेखाएँ तार के अक्ष के चारों ओर अक्ष के लम्बवत् तल में समकेन्द्रीय वृत्तों के रूप में होती हैं।
O को केन्द्र मानकर तार के अक्ष के लम्बवत् तल में त्रिज्या का एक वृत्त (बन्द वक्र) खींचे। यह वृत्त बिन्दु P से होकर गुजरता है। बिन्दु P पर उत्पन्न चुम्बकीय क्षेत्र B तथा अल्पांश ता के बीच का कोण 0° होगा। अतः ऐम्पियर के परिपथीय नियम से,
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}\) = µ₀I
या \(\oint \mathrm{B} d l\) cos 0 = µ₀I
\(\mathrm{B} \oint d l\) = µ₀I
किन्तु \(\oint d l\) = 2πr = वृत्त की परिधि
∴ B.2πr = µ₀I
या B= \(\frac{\mu_{0} 1}{2 \pi r}\)

प्रश्न 18.
यदि एक विद्युत्वाही चालक को किसी चुम्बकीय क्षेत्र में रखा जाये तो उस पर कार्य करने वाला बल किन-किन बातों पर निर्भर करता है ? इस बल का मान कब अधिकतम और कम न्यूनतम होता है, बल की दिशा क्या होती है ?
अथवा
चुम्बकीय क्षेत्र में धारावाही चालक पर बल का व्यंजक स्थापित कीजिए।
उत्तर-
मानलो एक चालक तार AB चुम्बकीय क्षेत्र B में रखा हुआ है। यदि इस तार में I विद्युत् धारा प्रवाहित की जाये तो विद्युत्वाही तार पर लगने वाला बल F

• तार में प्रवाहित विद्युत् धारा I के अनुक्रमानुपाती होता है अर्थात् F∝l.
• तार की लम्बाई । के अनुक्रमानुपाती होता है अर्थात् F∝l.
• चुम्बकीय क्षेत्र की तीव्रता B के अनुक्रमानुपाती होता है अर्थात् F∝B.
• sinθ के अनुक्रमानुपाती होता है जहाँ θ धारा और चुम्बकीय क्षेत्र के बीच का कोण है। अर्थात् F∝sinθ

उपर्युक्त चारों को मिलाकर लिखने पर, F∝ I/Bsinθ
F = KI/ Bsinθ
जहाँ K एक आनुपातिक नियतांक है। M.K.S. पद्धति में K = 1.
F = IlBsinθ
अधिकतम बल-यदि sinθ = 1 अर्थात् θ = 90° हो, तो
F = IlB sin 90° = IlB (अधिकतम)
अतः जब विद्युत्वाही तार चुम्बकीय क्षेत्र के लम्बवत् होता है, तो उस पर लगने वाला बल अधिकतम होता है। यह बल धारा की दिशा और चुम्बकीय क्षेत्र की दिशा दोनों के लम्बवत् होता है।

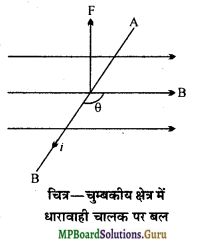
न्यूनतम बल-यदि sin θ = 0 अर्थात् θ = 0° हो, तो
F = IlBsin 0° = 0
अतः जब विद्युत्वाही चालक तार चुम्बकीय क्षेत्र के अनुदिश होता है तो उस पर लगने वाला बल शून्य । होता है।

प्रश्न 19.
फ्लेमिंग का बायें हाथ का नियम लिखिए।
उत्तर-
बायें हाथ का अंगूठा, तर्जनी तथा मध्यमा को इस प्रकार फैलाओ कि वे परस्पर लम्बवत् हों। अब यदि क्षेत्र की दिशा तर्जनी बल रेखाओं की दिशा (क्षेत्र की दिशा) एवं मध्यमा विद्युत् धारा की दिशा को प्रदर्शित करे तो अँगूठा चालक पर धारा की धारा की लगने वाले बल की दिशा को प्रदर्शित करेगा। दिशा इसे फ्लेमिंग का बायें हाथ का नियम कहते हैं।

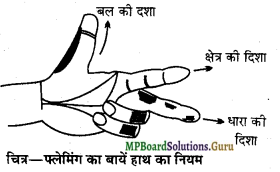
प्रश्न 20.
चुम्बकीय क्षेत्र में गतिमान आवेशित कण पर लगने वाले बल के लिए व्यंजक ज्ञात कीजिए। यह अधिकतम और न्यूनतम कब होता है ?
अथवा
लॉरेंज बल क्या है ? इसके लिए व्यंजक प्राप्त कीजिए। किस अवस्था में यह न्यूनतम और किस अवस्था में अधिकतम होता है ?
उत्तर-
लॉरेंज बल-चुम्बकीय क्षेत्र में गतिमान आवेश पर लगने वाले बल को लॉरेन्ज बल कहते हैं।
व्यंजक-हम जानते हैं कि यदि चुम्बकीय क्षेत्र B में स्थित / लम्बाई के तार में I विद्युत् धारा प्रवाहित की जाये तो उस पर लगने वाला बल F
(i) प्रवाहित आवेश q के अनुक्रमानुपाती होता है अर्थात्
F∝q
(ii) आवेश के वेग v के अनुक्रमानुपाती होता है अर्थात्
F∝v

(iii) चुम्बकीय क्षेत्र की तीव्रता B के अनुक्रमानुपाती होता है अर्थात्
F∝ B

(iv) sinθ के अनुक्रमानुपाती होता है जहाँ 0 धनावेश की दिशा एवं चुम्बकीय क्षेत्र की दिशा के बीच कोण है अर्थात्
F ∝ sinθ
उपर्युक्त चारों को मिलाने पर
F ∝qv B sin θ
या F= k.qv Bsinθ.
मात्रकों का चयन इस प्रकार किया जाता है कि k =1
∴F = qvBsinθ.
यही अभीष्ट व्यंजक है।

न्यूनतम-यदि θ = 0° हो अर्थात् आवेशित कण की गति चुम्बकीय क्षेत्र के समान्तर है, तो
sinθ = sin0° = 0
∴F=qvB x 0=0
अर्थात् यदि कोई आवेशित कण चुम्बकीय क्षेत्र के समान्तर गति करे तो उस पर कोई बल नहीं लगता, अर्थात् बल न्यूनतम होता है।

अधिकतम-यदि θ = 90° हो, तो
sinθ = sin 90° = 1
∴ आवेशित कण पर लगने वाला बल
F= qvB x 1
∴ F=qvB (अधिकतम) अर्थात् जब आवेशित कण चुम्बकीय क्षेत्र के लम्बवत् गति करता है, तो उस पर लगने वाला बल अधिकतम होता है।

प्रश्न 21.
एकसमान चुम्बकीय क्षेत्र में आवेशित कण के वृत्तीय मार्ग में गति के लिये
(i) वृत्तीय मार्ग की त्रिज्या तथा
(ii) कण के आवर्तकाल के लिये व्यंजक प्राप्त कीजिये।
उत्तर-
माना कि एक आवेशित कण जिस पर आवेश की मात्रा q है, B चुम्बकीय क्षेत्र में क्षेत्र के लम्बवत् y वेग से प्रवेश करती है, तो आवेश पर लगने वाला लॉरेंज बल
F= qvBsin90° = qvB ………………………….. (1)

फ्लेमिंग के बायें हाथ के नियमानुसार इस बल की दिशा वेग v और क्षेत्र B दोनों के लम्बवत् होगी।
इस प्रकार आवेशित कण पर बल F लग रहा है जो उसके वेग के लम्बवत् है, यह तभी सम्भव होगा जब आवेशित कण वृत्तीय पथ में गति – करे।

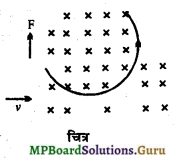
(i) इस वृत्तीय गति के लिये यह आवश्यक है कि लॉरेंज बल F आवेशित कण को आवश्यक अभिकेन्द्र बल प्रदान करे। यदि आवेशित कण का द्रव्यमान m तथा वृत्तीय पथ की त्रिज्या r हो, तो
लॉरेंज बल = अभिकेन्द्र बल
या qvB = \(\frac{m v^{2}}{r_{ }}\)
या r = \(\frac{m v}{q \mathrm{~B}}\) ……………………………… (1)
या r = \(\frac{p}{q B}\) (जहाँ mv=p कण का संवेग) …………………………….. (2)
यही अभीष्ट व्यंजक है।

या T=\(\frac{2 \pi r}{v}\)
समी. (1) से r का मान रखने पर,
T = \(\frac{2 \pi m v}{v \cdot q B}\)
या T = \(\frac{2 \pi m}{q \mathrm{~B}}\) ………………………….. (3)
यही अभीष्ट व्यंजक है।

प्रश्न 22.
दो समान्तर तार जिनमें विपरीत दिशा में धारा प्रवाहित हो रही है, एक-दूसरे को प्रतिकर्षित करते हैं, क्यों?
उत्तर-
मानलो AB और CD दो समान्तर तार हैं जिनमें विपरीत दिशा में धारा प्रवाहित हो रही है। तार AB में प्रवाहित धारा के कारण CD पर चुम्बकीय क्षेत्र की दिशा कागज के तल के लम्बवत् नीचे की ओर होगी। अतः फ्लेमिंग के बायें हाथ के नियमानुसार CD पर AB की विपरीत दिशा में बल लगेगा अर्थात् दोनों तार एक-दूसरे को प्रतिकर्षित करेंगे।

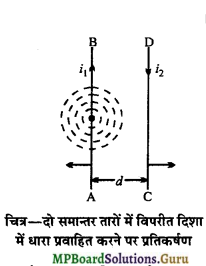
प्रश्न 23.
दो लम्बे, सीधे और समान्तर चालकों में एक ही दिशा में धारा प्रवाहित करने पर क्या प्रभाव पड़ेगा?
अथवा
दो समान्तर चालक जिनमें एक ही दिशा में धारा प्रवाहित हो रही है, एक-दूसरे को आकर्षित करते हैं, क्यों ?
उत्तर-
दो लम्बे, सीधे और समान्तर चालकों में एक ही दिशा में धारा प्रवाहित करने पर वे एक-दूसरे को आकर्षित करते हैं। मानलो AB और CD दो समान्तर चालक हैं, जिनमें एक ही दिशा में धारा प्रवाहित हो रही है। चालक AB में प्रवाहित धारा के कारण CD पर चुम्बकीय क्षेत्र की दिशा कागज के तल के लम्बवत् नीचे की ओर होगी। अतः फ्लेमिंग के बायें हाथ के नियमानुसार चालक
CD पर AB की दिशा में बल लगेगा अर्थात् दोनों चालक एक-दूसरे को आकर्षित करेंगे।

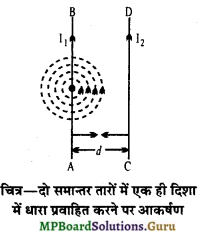
प्रश्न 24.
दो तार जिनमें I₁ और I₂ धारा प्रवाहित हो रही है, एक-दूसरे के समान्तर d दूरी पर रखे हुए हैं। दूसरे तार की प्रति एकांक लम्बाई पर लगने वाले बल के लिए व्यंजक प्राप्त कीजिए। यह कब आकर्षण बल होगा और कब प्रतिकर्षण बल ?
अथवा
दो समान्तर विद्यतवाही चालकों के मध्य लगने वाले बल के व्यंजक व्युत्पन्न कीजिए। यह कब आकर्षण बल होगा और कब प्रतिकर्षण बल ?
अथवा
दो समान्तर एक ही दिशा में धारावाही चालकों के बीच बल का व्यंजक व्युत्पन्न कीजिए।
उत्तर-
मानलो AB और CD दो समान्तर चालक तार हैं, जो एक-दूसरे से d दूरी पर स्थित हैं। यदि तार AB में धारा I₁ प्रवाहित करें तो उसके चारों ओर चुम्बकीय क्षेत्र उत्पन्न हो जाता है।

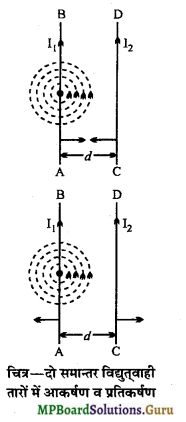
चालक AB से d दूरी पर चुम्बकीय क्षेत्र की तीव्रता
B= \(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 \mathrm{I}_{1}}{d}\)
इस क्षेत्र की दिशा कागज के तल के लम्बवत् नीचे की ओर होगी। इस क्षेत्र में एक दूसरा तार CD जिसमें धारा i₂ प्रवाहित हो रही है, विद्युत् क्षेत्र के लम्बवत् स्थित है।

अत: चालक तार CD के l लम्बाई पर लगने वाला बल
F= I₂lB
या F = I₂l\(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 \mathrm{I}_{1}}{d}\)
या F = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 \mathrm{I}_{1} \mathrm{I}_{2} l}{d}\)

अत: चालक तार CD के प्रति एकांक लम्बाई पर लगने वाला बल
\(\frac{\mathrm{F}}{l}\) = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 \mathrm{I}_{1} \mathrm{I}_{2}}{d}\)
d यदि दोनों चालक तारों में विद्युत् धारा की दिशा समान है, तो फ्लेमिंग चित्र-दो समान्तर विद्युत्वाही तारों में आकर्षण व प्रतिकर्षण के बायें हाथ के नियमानुसार CD पर AB की दिशा में बल लगेगा अर्थात् त दोनों चालक तार एक-दूसरे को आकर्षित करेंगे।
यदि दोनों चालक तारों में विद्युत् धारा की दिशा विपरीत है, तो CD पर AB के विपरीत दिशा में बल लगेगा अर्थात् दोनों चालक तार एक-दूसरे को प्रतिकर्षित करेंगे।

प्रश्न 25.
चल कुण्डली धारामापी का रेखाचित्र बनाकर उसकी रचना लिखिए।
उत्तर-
इसमें एक स्थायी नाल चुम्बक होता है, जिसके ध्रुव खण्ड NS मुलायम लोहे के बने होते हैं तथा अवतल बेलनाकार कटे होते हैं। इनके बीच एक कुण्डली A, फॉस्फर ब्रांज की पत्ती F की सहायता से लटका दी जाती है। कुण्डली के दूसरे सिरे का सम्बन्ध स्प्रिंग S से होता है। कुण्डली ताँबे के पृथक्कृत तार को ऐल्युमिनियम के फ्रेम पर लपेटकर बनायी जाती है । इसके मध्य के रिक्त स्थान में नर्म लोहे का क्रोड C होता है जो कि कुण्डली को कहीं भी स्पर्श नहीं करता। पत्ती F और स्प्रिंग S का सम्बन्ध आधार में लगे संयोजक पेंच T₁ और T₂ से होता है । पत्ती F में एक समतल वृत्ताकार दर्पण M लगा रहता है जिस पर प्रकाश डालकर लैम्प पैमाना व्यवस्था द्वारा कुण्डली का विक्षेप ज्ञात किया जाता है। यह सारा प्रबन्ध अचुम्बकीय पदार्थ के बने एक बॉक्स में बन्द कर दिया जाता है ताकि धूल, वायु इत्यादि का कोई प्रभाव न पड़े। बॉक्स के सामने की दीवार काँच की बनी होती है तथा आधार में समतलकारी पेंच लगे होते हैं।

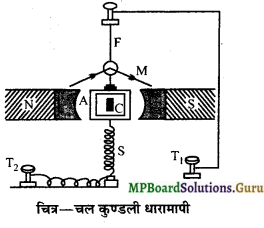
प्रश्न 26.
चल कुण्डली धारामापी का सिद्धान्त क्या है ? सिद्ध कीजिए कि कुण्डली में प्रवाहित धारा, कुण्डली में उत्पन्न विक्षेप के अनुक्रमानुपाती होती है।
अथवा
एकसमान चुम्बकीय क्षेत्र में स्थित धारावाही आयताकार कुण्डली पर आरोपित बल आघूर्ण के लिए व्यंजक स्थापित कीजिए।
(i) अधिकतम और
(ii) न्यूनतम बल आघूर्ण के लिए क्या परिस्थितियाँ होंगी?
उत्तर-
चल कुण्डली धारामापी इस सिद्धांत पर आधारित है कि जब एक विद्युत्वाही चालक को चुम्बकीय क्षेत्र में रखा जाता है, तो इस पर एक बल कार्य करने लगता है।
चित्र में एक आयताकार कुण्डली ABCD एकसमान चुम्बकीय क्षेत्र B में इस प्रकार लटकाई गई है कि भुजा AB तथा CD क्षेत्र के लम्बवत् रहें । मानलो AB = CD = l और BC = AD = b है। यदि कुण्डली में धारा I दिखाई गई दिशा में बहे तो फ्लेमिंग के बायें हाथ के नियम के अनुसार भुजा AB पर कागज के तल के लम्बवत् ऊपर की ओर और भुजा CD पर कागज के तल के लम्बवत् नीचे की ओर BIl बल कार्य करेगा। ये बल बराबर तथा विपरीत होने के कारण बलयुग्म बनाते हैं, जिसके कारण कुण्डली विक्षेपित हो जाती है।

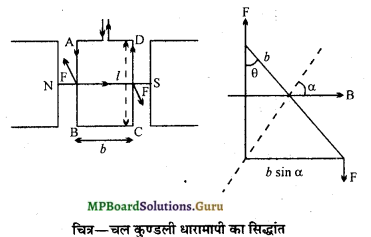
यदि कुण्डली के तल पर या लम्ब क्षेत्र की दिशा में α कोण बनाता हो, तो
विक्षेपक बलयुग्म का आघूर्ण = Bll x b sin α
= B I A sin α, (∴ A = lb)
= nBI A sin α, (n = फेरों की संख्या) …………………………….(1)
= nBIA, (∵ त्रिज्या क्षेत्र के लिए α = 90° ∴ sin α = 1)

यदि साम्यावस्था से कुण्डली का विक्षेप θ हो, तो ऐंठन बलयुग्म का आघूर्ण = C.θ, (C = एकांक ऐंठन का आघूर्ण)
∴ सन्तुलन की अवस्था में,
nBIA = C.θ
∴ I = \(\frac{\mathrm{C}}{n \mathrm{BA}}\) θ
∴ I = K.θ, (जहाँ K = \(\frac{\mathrm{C}}{n \mathrm{BA}}\) = धारामापी का नियतांक)
⇒ I∝θ

अर्थात् कुण्डली में प्रवाहित धारा, कुण्डली में उत्पन्न विक्षेप के अनुक्रमानुपाती होती है।
यही चल कुण्डली धारामापी का सिद्धान्त है।
(i) अधिकतम होने के लिए परिस्थिति-समीकरण (1) में यदि α = 90° हो, तो
τ = nBIA sin 90°
= n BIA (अधिकतम)
अतः जब कुण्डली का तल चुम्बकीय क्षेत्र के समान्तर होता है तो उस पर लगने वाला बल आघूर्ण अधिकतम होता है।

(ii) न्यूनतम होने के लिए परिस्थिति-
समीकरण ( 1 ) में यदि α= 0⁰ हो तो
τ =nBIA sin 0°
= 0 (न्यूनतम)
अतः जब कुण्डली का तल चुम्बकीय क्षेत्र के लम्बवत् होता है तो उस पर लगने वाला बल आघूर्ण शून्य (न्यूनतम ) होता है।

प्रश्न 27.
चल कुण्डली धारामापी की सुग्राहिता से आप क्या समझते हैं ? इसके लिए व्यंजक लिखिए। इसकी सुग्राहिता किन-किन कारकों पर निर्भर करती है और किस प्रकार ?
उत्तर-
कुण्डली में एकांक धारा प्रवाहित करने पर उसमें उत्पन्न विक्षेप को धारामापी की सुग्राहिता कहते हैं। यदि धारामापी में I धारा प्रवाहित करने पर उसकी कुण्डली में उत्पन्न विक्षेप θ हो, तो
I = \(\frac{\mathrm{C}}{n \mathrm{BA}}\).θ
या \(\frac{\theta}{\mathrm{I}}\) = \(\frac{n \mathrm{BA}}{\mathrm{C}}\)

अतः धारामापी की सग्राहिता S = \(\frac{\theta}{\mathrm{I}}\) = \(\frac{n \mathrm{BA}}{\mathrm{C}}\)
धारामापी की सुग्राहिता निम्नलिखित कारकों पर निर्भर करती है-

• फेरों की संख्या n पर-यदि कुण्डली में फेरों की संख्या अधिक है, तो उसकी सुग्राहिता अधिक होगी।
• चुम्बकीय क्षेत्र की तीव्रता B पर-यदि चुम्बक शक्तिशाली है, तो धारामापी की सुग्राहिता अधिक होगी।
• कुण्डली के क्षेत्रफल A पर-यदि कुण्डली का क्षेत्रफल अधिक है, तो धारामापी की सुग्राहिता अधिक होगी।
• निलम्बन तार की प्रकृति पर-यदि निलम्बन तार के लिए एकांक ऐंठन का आघूर्ण कम है, तो धारामापी की सुग्राहिता अधिक होगी। इसके लिए फॉस्फर ब्रांज की पत्ती को लम्बी तथा पतली होनी चाहिए।

प्रश्न 28.
चल कुण्डली धारामापी की चार विशेषताएँ लिखिए।
अथवा
किन्हीं तीन बिन्दुओं के अन्तर्गत बताइए कि चल कुण्डली धारामापी स्पर्शज्या धारामापी से किस प्रकार श्रेष्ठ है ? .
उत्तर-
चल कुण्डली धारामापी को स्पर्शज्या धारामापी से श्रेष्ठ मानते हैं। इसके निम्न कारण हैं

1. इसे किसी भी स्थिति में रखकर प्रयोग कर सकते हैं।
2. इस पर बाह्य चुम्बकीय क्षेत्र का प्रभाव कम पड़ता है।
3. इसकी सुग्राहिता अधिक होती है।
4. इसे अमीटर और वोल्टमीटर में परिवर्तित कर सकते हैं।
5. इसके दोलन शीघ्र समाप्त हो जाते हैं।
6. इसमें धारा विक्षेप के अनुक्रमानुपाती होती है, अतः संकेतक द्वारा धारा का मान सीधे ही पढ़ा जा सकता है।

प्रश्न 29.
शण्ट क्या है ? इसका उपयोग लिखिए। इससे होने वाले लाभ व हानि लिखिए।
उत्तर-
शण्ट-शण्ट कम प्रतिरोध का तार होता है, जिसे धारामापी की कुण्डली के साथ समान्तर क्रम में जोड़ा जाता है।
उपयोग-धारामापी में शण्ट लगाकर उसे अमीटर में परिवर्तित किया जाता है। .
लाभ-

• धारामापी की कुण्डली और संकेतक क्षतिग्रस्त होने से बच जाते हैं।
• धारामापी का प्रभावी प्रतिरोध बहुत कम हो जाता है। अतः उसे किसी परिपथ में जोड़ने पर उस परिपथ में बहने वाली धारा के मान में कोई उल्लेखनीय परिवर्तन नहीं होता है।
• इसकी सहायता से अमीटर के परास को बढ़ाया जा सकता है। हानि-शण्ट लगाने से धारामापी की सुग्राहिता कम हो जाती है।

प्रश्न 30.
शण्ट क्या है ? शण्ट का सिद्धान्त समझाइए।
अथवा
शण्ट की आवश्यकता को स्पष्ट करते हुए दिखाइए कि शण्ट और धारामापी में प्रवाहित होने वाली विद्युत् धाराएँ उनके प्रतिरोधों के व्युत्क्रमानुपाती होती हैं।
उत्तर-
शण्ट-उपर्युक्त प्रश्न देखिए।
सिद्धान्त-मानलो धारामापी की कुण्डली का प्रतिरोध G तथा शण्ट का प्रतिरोध S है। परिपथ में प्रवाहित होने वाली मुख्य धारा का मान I है। इसका I_g भाग धारामापी में से और I_s भाग शण्ट में से होकर प्रवाहित होता है।

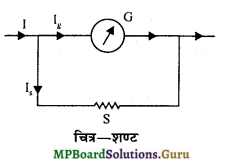
स्पष्ट है कि
I = I_g +I_s …………………… (1)

ओम के नियमानुसार, धारामापी के सिरों के बीच विभवान्तर = I_g.G
तथा शण्ट के सिरों के बीच विभवान्तर = I_s.S
∵ धारामापी और शण्ट समान्तर क्रम में जुड़े हैं।
∴ I_g.G = I_s.S
\(\frac{\mathrm{I}_{s}}{\mathrm{I}_{g}}\) = \(\frac{G}{S}\) ………………………….. (2)
समी. (2) के दोनों पक्षों में 1 जोड़ने पर,

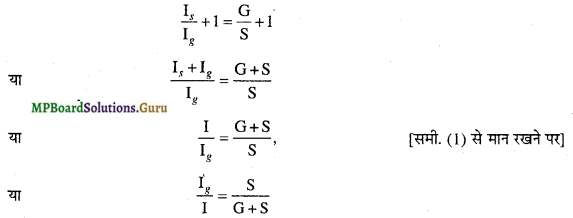
यदि मुख्य धारा का n वाँ भाग धारामापी से प्रवाहित हो, तो

∴ S = \(\frac{\mathrm{G}}{n-1}\)
अर्थात् यदि मुख्य धारा का n वाँ भाग धारामापी में से प्रवाहित करना चाहते हैं, तो शण्ट के प्रतिरोध को धारामापी के प्रतिरोध का (n- 1) वाँ भाग होना चाहिए।
यही शण्ट का सिद्धान्त है। समी. (2) से स्पष्ट है कि
I_s ∝ \(\frac{1}{\mathrm{~S}}\) तथा I_g ∝ \(\frac{1}{\mathrm{G}}\)
अतः शण्ट में बहने वाली धारा शण्ट के प्रतिरोध के व्युत्क्रमानुपाती तथा धारामापी में बहने वाली धारा धारामापी के प्रतिरोध के व्युत्क्रमानुपाती होती है।

प्रश्न 31.
चल कुण्डली धारामापी को अमीटर और वोल्टमीटर में कैसे परिवर्तित किया जाता है ?
उत्तर-
(i) धारामापी को अमीटर में परिवर्तित करना-अमीटर का प्रतिरोध कम होना चाहिए। अतः धारामापी को अमीटर में परिवर्तित करने के लिए उसकी कुण्डली के साथ समान्तर क्रम में कम प्रतिरोध का तार, जिसे शण्ट कहते हैं, जोड़ देते हैं।
चित्र में G धारामापी का प्रतिरोध तथा S शण्ट है। मानलो धारामापी की कुण्डली का प्रतिरोध G तथा शण्ट का प्रतिरोध S है। यदि मुख्यधारा का I_g भाग धारामापी की कुण्डली में से होकर प्रवाहित हो तो शण्ट में प्रवाहित होने वाली धारा का मान (I – I_g) होगा।। धारामापी और शण्ट समान्तर क्रम में जुड़े हैं।

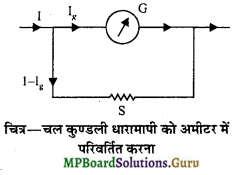
∴ (I-I_g)S = I_g.G
या S= \(\frac{\mathrm{G} \cdot \mathrm{I}_{g}}{\mathrm{I}-\mathrm{I}_{g}}\)
इस प्रकार जब इस मान को शण्ट धारामापी के साथ लगा दिया जाता है तो वह 0- I ऐम्पियर परास के अमीटर में परिवर्तित हो जाता है।

(ii) धारामापी को वोल्टमीटर में परिवर्तित करना-वोल्टमीटर का प्रतिरोध अधिक होता है। अतः धारामापी को वोल्टमीटर में परिवर्तित करने के लिए उसकी कुण्डली के साथ श्रेणीक्रम में उच्च प्रतिरोध का तार जोड़ देते हैं।
मानलो G धारामापी का प्रतिरोध तथा R श्रेणीक्रम में जोड़ा जाने वाला प्रतिरोध है।
यदि I_g धारा प्रवाहित करने से संकेतक पूर्ण स्केल विक्षेप देता हो तो

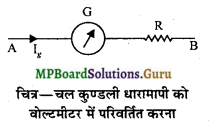
V = I_g (G+R)
या G+R = \(\frac{\mathrm{V}}{\mathrm{I}_{g}}\)
या R = \(\frac{\mathrm{V}}{\mathrm{I}_{g}}\) – G
इस प्रकार जब इस मान को उच्च प्रतिरोध धारामापी की कुण्डली के साथ श्रेणीक्रम में संयोजित कर दिया जाता है तो वह 0 – V वोल्ट परास के वोल्टमीटर में परिवर्तित हो जाता है।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
बायो-सेवर्ट नियम द्वारा किसी धारावाही वृत्तीय कुण्डली के अक्ष पर स्थित किसी बिन्दु पर चुम्बकीय क्षेत्र की तीव्रता हेतु व्यंजक ज्ञात कीजिए।
उत्तर-
मानलो a त्रिज्या का एक वृत्तीय लूप है, जिसमें I विद्युत् धारा तीर की दिशा में प्रवाहित हो रही है। लूप के अक्ष पर उसके केन्द्र O से x दूरी पर एक बिन्दु P है, जिस पर चुम्बकीय क्षेत्र की तीव्रता ज्ञात करनी है। मानलो लूप का तल कागज के तल के लम्बवत् तथा उसका अक्ष OP कागज के तल पर स्थित है। लूप को कई अल्पांशों में विभक्त कीजिए।
मानलो लूप के ठीक ऊपरी सिरे पर dl लम्बाई का एक अल्पांश AB है। इस अल्पांश से बिन्दु P की दूरी r है।
अत: इस अल्पांश AB के कारण बिन्दु P पर चुम्बकीय क्षेत्र की तीव्रता
dB = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{\mathrm{I} \cdot d l \cdot \sin \theta}{r^{2}}\)
जहाँ θ, अल्पांश AB और अल्पांश को बिन्दु P से मिलाने वाली रेखा के बीच का कोण है। स्पष्ट है कि
θ = 90°
∴ dB = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{\mathrm{I} . d l . \sin 90}{r^{2}}\)
या dB = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{\mathrm{I} . d l}{r^{2}}\) …………………………. (1)

इस क्षेत्र dB की दिशा अल्पांश AB और इस अल्पांश को बिन्दु P से मिलाने वाली रेखा के लम्बवत् तल में PR के अनुदिश होगी।
मानलो ∠CPO = dB को दो घटकों में वियोजित किया जा सकता है
(i) dBsin Φ अक्ष OP के अनुदिश और
(ii) dBcosΦ अक्ष OP के लम्बवत् PN दिशा में।
यदि लूप के ठीक निचले सिरे पर व्यासाभिमुखी उतनी ही लम्बाई वा का एक दूसरा अल्पांश A’B’ लें, तो इस अल्पांश के कारण भी बिन्दु P पर चुम्बकीय क्षेत्र की तीव्रता dB = \( \frac{\mu_{0}}{4 \pi} \cdot \frac{\mathrm{I} d l}{r^{2}}\) होगी, किन्तु अब इसकी दिशा PR’ के अनुदिश होगी।

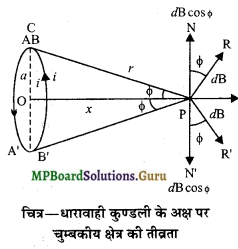
dB को पुन: दो घटकों में वियोजित किया जा सकता है
(i) dBsinΦ अक्ष OP के अनुदिश और
(ii) dB cosΦ अक्ष OP के लम्बवत् PN’ दिशा में।
चूँकि PN और PN’ एक-दूसरे के विपरीत हैं, अक्ष OP के लम्बवत् घटक एक-दूसरे को निरस्त कर देते हैं। स्पष्ट है कि वृत्तीय लूप के सभी अल्पांशों के कारण जो घटक अक्ष OP के लम्बवत् होंगे, एक-दूसरे को निरस्त कर देंगे, किन्तु अक्ष OP के अनुदिश सभी घटक आपस में जुड़ जायेंगे। अतः वृत्तीय लूप के कारण बिन्दु P पर अक्ष के अनुदिश चुम्बकीय क्षेत्र की तीव्रता
B= ΣdBsinΦ
या B =Σ\(\frac{\mu_{0}}{4 \pi} \cdot \frac{\mathrm{I} d l}{r^{2}} \sin \phi\) ……………………………. (2)

परन्तु sinΦ = \(\frac{a}{r}\)
समी. (2) में मान रखने पर,
B = Σ \(\frac{\mu_{0}}{4 \pi} \cdot \frac{\mathrm{I} d l}{r^{2}} \cdot \frac{a}{r}\)
= \(\frac{\mu_{0}}{4 \pi}+\Sigma \frac{\mathrm{I} d l . a}{r^{3}}=\frac{\mu_{0}}{4 \pi} \cdot \frac{\mathrm{I} a}{r^{3}} \Sigma d l\)
= \(\frac{\mu_{0}}{4 \pi} \cdot \frac{\mathrm{I} a}{r^{3}} \).2πa, [∵Σdl = 2πa = लूप की परिधि ]
अतः B= \(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 \pi \mathrm{I} a^{2}}{r^{3}}\) ……………………….. (3)

समकोण ΔCOP में,
r² = a²+x²
∴ r = (a²+x²)^1/2
∴ r³ = (a²+x²)^1/2
समी. (3) में मान रखने पर,

B = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 \pi \mathrm{L} a^{2}}{\left(a^{2}+x^{2}\right)^{3 / 2}}\) वेबर/ मीटर²
यदि n फेरों वाली वृत्तीय कुण्डली बनायी जाये, तो
B= \(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 \pi n \mathrm{a}^{2}}{\left(a^{2}+x^{2}\right)^{3 / 2}}\)
धारावाही कुंडली के केंद्र पर तीव्रता (x = 0 पर) अधिकतम होती है।
B = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 \pi I n}{a}\).

प्रश्न 2.
साइक्लोट्रॉन क्या है ? इसका सिद्धान्त लिखिये तथा निम्नलिखित के लिये व्यंजक ज्ञात कीजिये.
(i) आवर्तकाल,
(ii) साइक्लोट्रॉन आवृत्ति,
(iii) प्राप्त ऊर्जा।
उत्तर-
साइक्लोट्रॉन-साइक्लोट्रॉन एक ऐसी युक्ति है जिसका उपयोग धनावेशित कणों जैसे प्रोटॉनों, α-कण इत्यादि को त्वरित करने में किया जाता है।
सिद्धान्त- साइक्लोट्रॉन इस तथ्य पर आधारित है कि जब एक आवेशित कण एकसमान चुम्बकीय क्षेत्र में लंबवत् गति करता है तथा विद्युत् क्षेत्र द्वारा लगातार त्वरित होता है तो वह बढ़ती हुयी त्रिज्या के सर्पिलाकार पथ का अनुसरण करता है तथा उसकी चाल लगातार बढ़ती चली जाती है।

माना एक धनावेशित कण जैसे, प्रोटॉन चुम्बकीय क्षेत्र के लंबवत् गति करता है तो उस पर लगने वाला लॉरेन्ज बल
F= qvBsin 90° = qvB
यही बल प्रोटॉन को डीज के अंदर वृत्तीय गति करने के लिये आवश्यक अभिकेन्द्रीय बल प्रदान करता है। माना वृत्तीय मार्ग की त्रिज्या r है तो अभिकेन्द्रीय बल mv²/r होगा। ∴ qvB= \(\frac{m v^{2}}{r}\) या r = \(\frac{m v}{q \mathrm{~B}}\) …………………… (1)

डीज के अंदर अर्द्धवृत्ताकार मार्ग में गति करने के लिये कण द्वारा लगाया गया समय

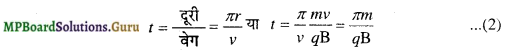
अतः यह स्पष्ट है कि धनावेशित कण द्वारा एक अर्द्धवृत्ताकार मार्ग तय करने में लगाया गया समय समान होता है। यह त्रिज्या पर निर्भर नहीं करता है।
(i) आवर्तकाल-माना एक वृत्ताकार मार्ग में गति करने में लगा समय (आवर्तकाल) T है तो डीज की ध्रुवता T/2 समय में परिवर्तित होती है।
∴ \(\frac{\mathrm{T}}{2}\) = t = \(\frac{\pi m}{q \mathrm{~B}}\)
या T = \(\frac{2 \pi m}{q \mathrm{~B}}\) ……………………….. (3)
(ii) साइक्लोट्रॉन आवृत्ति-साइक्लोट्रॉन आवृत्ति को चुम्बकीय अनुनादी आवृत्ति भी कहते हैं।
∴ υ = \(\frac{1}{\mathrm{~T}}\) = \(\frac{q \mathrm{~B}}{2 \pi m}\) ……………………… (4)
तथा साइक्लोट्रॉन कोणीय आवृत्ति ω = 2πυ = \(\frac{q \mathrm{~B}}{m}\) ………………………………. (5)

(iii) प्राप्त ऊर्जा-आवेशित कण द्वारा प्राप्त ऊर्जा
E = \(\frac{1}{2}\)mv²
समीकरण (1) से, v = \(\frac{q r B}{m}\)
∴ E = \(\frac{1}{2}\)m\(\left(\frac{q r B}{m}\right)^{2}\) या E = \(\frac{q^{2} \mathrm{~B}^{2} r^{2}}{2 m}\) ………………………………… (6)
⇒ E ∝ r²

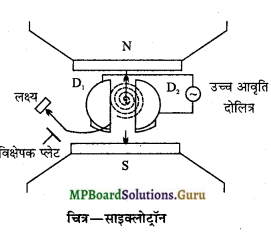
प्रश्न 3.
साइक्लोट्रॉन का सैद्धान्तिक चित्र बनाइये तथा इसकी कार्यविधि एवं सीमाएँ लिखिये।
उत्तर-
चित्र में साइक्लोट्रॉन की संरचना प्रदर्शित की गयी है। इसमें D-आकार के दो धात्विक चेम्बर होते हैं जिन्हें डीज कहा जाता है। इन डीज (D₁ व D₂) के बीच गेप होता है जहाँ पर आवेशित कणों का स्रोत रखा जा सकता है। डीज का संबंध एक उच्च आवृत्ति दोलित्र से होता है । यह संपूर्ण व्यवस्था दो प्रबल चुंबकीय ध्रुव खंडों N व S के बीच में रखा होता है।
कार्य-विधि- माना किसी क्षण आयन स्रोत O से m द्रव्यमान तथा q आवेश का धनायन उत्पन्न होता है। माना इस क्षण D₁ ऋणात्मक विभव पर तथा D₁ धनात्मक विभव पर है अतः धनायन D₁ की ओर त्वरित होता है तथा उसके अंदर प्रवेश कर जाता है । खोखले चालक D₁ के अंदर विद्युत् क्षेत्र शून्य होता है अत: उस पर केवल चुम्बकीय क्षेत्र ही कार्य करता है जो उसे वृत्तीय पथ में मोड़ देता है। D₁ में अर्द्धवृत्तीय गति करने के पश्चात् धनायन पुनः विद्युत् क्षेत्र के संपर्क में आता है। विद्युत् क्षेत्र की आवृत्ति को इस प्रकार समायोजित किया जाता है कि ज्यों ही धनायन D₁ से बाहर निकलता है, D₂ ऋणात्मक विभव पर तथा D₁ दोलित्र धनात्मक विभव पर आ जाता है। अब धनायन D₂ की ओर त्वरित होता है।
यह त्रिज्या बार-बार दुहरायी जाती है तथा धनायन अत्यधिक त्वरित हो जाता है, फिर इसे खिड़की से बाहर निकाला जाता है एवं लक्ष्य पर टकराता है।

साइक्लोट्रॉन की सीमाएँ
(i) साइक्लोट्रॉन की सहायता से इलेक्ट्रॉनों को त्वरित नहीं किया जा सकता। इलेक्ट्रॉन का द्रव्यमान बहुत कम होता है। अत: थोड़ी-सी भी ऊर्जा देने पर उसकी चाल अत्यधिक बढ़ जाती है । फलस्वरूप उसकी आवृत्ति को दोलायमान विद्युत्-क्षेत्र की आवृत्ति के बराबर कर पाना सम्भव नहीं है।
(ii) साइक्लोट्रॉन की सहायता से अनावेशित कणों जैसे-न्यूट्रॉन आदि को त्वरित नहीं किया जा सकता।
(iii) साइक्लोट्रॉन में धनायन को एक निश्चित सीमा की चाल से अधिक त्वरित नहीं किया जा सकता।

प्रश्न 4.
ऐम्पियर का परिपथीय नियम लिखिए एवं इसकी सहायता से धारावाही परिनालिका के अन्दर चुम्बकीय क्षेत्र हेतु व्यंजक व्युत्पन्न कीजिए।
अथवा
दर्शाइए कि परिनालिका के भीतर तीव्रता सिरे की तीव्रता की दुगुनी होती है।
उत्तर-
ऐम्पियर का परिपथीय नियम-लघु उत्तरीय प्रश्न क्रमांक 16 देखिए।
मानलो XY एक परिनालिका है। इसकी त्रिज्या a तथा इसकी प्रति एकांक लम्बाई पर फेरों की संख्या n है। मानलो परिनालिका में धारा I प्रवाहित हो रही है।

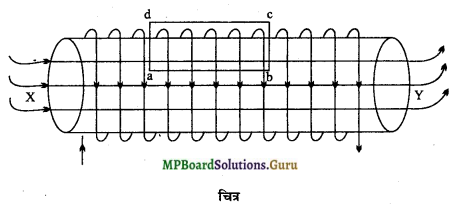
एक बंद परिपथ abcd की कल्पना करो। मानलो भुजाएँ ab और cd परिनालिका की लम्बाई के समान्तर हैं। तब बंद परिपथ abcd के लिए ऐम्पियर के परिपथीय नियम से,
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}\) = \(\int_{a}^{b} \overrightarrow{\mathrm{B}} d \vec{l}+\int_{b}^{c} \overrightarrow{\mathrm{B}} d \vec{l}+\int_{c}^{l} \overrightarrow{\mathrm{B}} d \vec{l}+\int_{d}^{a} \overrightarrow{\mathrm{B}} d l\) …………………………. (1)
और \(\int_{a}^{b} \overrightarrow{\mathrm{B}} d \vec{l}\) = \(\int_{a}^{b} \mathrm{~B} d l\) coso° ,
(∵ भुजा ab चुम्बकीय क्षेत्र के अनुदिश है)
= \(\int_{a}^{b} \mathrm{~B} d l\) = B \(\int_{a}^{b} d l \)

समी. (1) में मान रखने पर,
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}\) = BL+0+0+ 0 = BL ………………………. (2)
किन्तु ऐम्पियर के परिपथीय नियम से,
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}\) = µ_o × आयत abcd से घिरी कुल धारा
= µ_onLI ………………………………….. (3)
समी. (2) और (3) से,
BL = µ_onLI
या B = µ_onI
यही परिनालिका के अन्दर किसी बिन्दु पर चुम्बकीय क्षेत्र के लिए व्यंजक है।

आंकिक प्रश्न
प्रश्न 1.
एक लम्बे सीधे तार में 10 ऐम्पियर की धारा बह रही है। तार से 10 मीटर की दूरी पर चुम्बकीय क्षेत्र की तीव्रता ज्ञात कीजिए।
उत्तर-
हल : सूत्र : B= \(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 I}{d}\) = 10^-7 × \(\frac{2 \mathrm{I}}{d}\) टेस्ला
दिया है : I = 10 ऐम्पियर, d = 10 मीटर
सूत्र में मान रखने पर,
B = 10^-7 × \(\frac{2 \times 10}{10}\) टेस्ला।

प्रश्न 2.
एक वृत्तीय कुण्डली का व्यास 0.2 मीटर है तथा इसमें तार के 1000 फेरे लपेटे गये हैं। यदि कुण्डली में 0.1 ऐम्पियर की धारा प्रवाहित हो रही है तो उसके केन्द्र पर चुम्बकीय क्षेत्र की तीव्रता ज्ञात कीजिए।
उत्तर-
हल : सूत्र : B= \(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 \pi n \mathrm{I}}{r}\) = 10^-7 × \(\frac{2 \pi n \mathrm{I}}{r}\) टेस्ला
दिया है : n = 1000, 2r = 0.2 मीटर या r = 0.1 मीटर, I = 0.1 ऐम्पियर ।
सूत्र में मान रखने पर,
B = \(\frac{10^{-7} \times 2 \times 3 \cdot 14 \times 1000 \times 0 \cdot 1}{0 \cdot 1}\)
= 6.28 × 10^-4 टेस्ला।

प्रश्न 3.
एक धारामापी का प्रतिरोध 50 ओम है। जब इसमें 0.01 ऐम्पियर की धारा प्रवाहित होती है, तो धारामापी में पूर्ण स्केल विक्षेप प्राप्त होता है। धारामापी को
(i) 5 ऐम्पियर परास के अमीटर,
(ii) 5 वोल्ट परास के वोल्टमीटर में कैसे बदलोगे?
उत्तर-
हल : दिया है :G=50 ओम, I_g = 0.01 ऐम्पियर
(i) मानलो कुण्डली के साथ समान्तर क्रम में S प्रतिरोध का शण्ट जोड़ा गया है।
I = 5 ऐम्पियर
सूत्र : S = \(\frac{\mathrm{I}_{e} \times \mathrm{G}}{\mathrm{I}-\mathrm{I}_{g}}\) में मान रखने पर,
= \(\frac{0 \cdot 01 \times 50}{5-0 \cdot 01}\) = \(\frac{50}{499}\) ओम।

(ii) मानलो कुण्डली के साथ श्रेणीक्रम में R प्रतिरोध का तार जोड़ा जाता है।
तब R=\(\frac{V}{I_{g}}-G\) = \(\frac{5}{0 \cdot 01}-50\) = 450 ओम।

प्रश्न 4.
एक साइक्लोट्रॉन दोलित्र की आवृत्ति 10Hz है। प्रोटॉन को त्वरित करने के लिए आवश्यक चुम्बकीय क्षेत्र कितना होगा?
उत्तर-
हल : µ = \(\frac{q \mathrm{~B}}{2 \pi m}\), B = \(\frac{2 \pi \mathrm{cm} \mathrm{u}}{q}\)
दिया है : m = 1.67 × 10^-27 किग्रा, υ = 10 Hz; q= 1.6 × 10^-19 कूलॉम
अतः B = \(\frac{2 \times 3 \cdot 14 \times 1.67 \times 10^{-27} \times 10}{1 \cdot 6 \times 10^{-19}}\) = 65.55 × 10^-8 = 6.6 × 10^-7 टेस्ला।

प्रश्न 5.
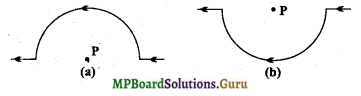
एक सीधे तार को जिसमें 12 ऐम्पियर की धारा प्रवाहित हो रही है, चित्रानुसार 2 सेमी त्रिज्या के अर्धवृत्ताकार चाप में मोड़ा गया है। इस वृत्ताकार चाप के केंद्र पर चुंबकीय क्षेत्र की दिशा तथा परिमाण ज्ञात कीजिए।
क्या होगा यदि तार को उसी त्रिज्या के अर्धवृत्ताकार चाप में किंतु विपरीत दिशा में मोड़ दिया जाए?
उत्तर-

हल-धारा अवयव के कारण किसी बिंदु पर चुंबकीय क्षेत्र dB = \(\frac{\mu_{0}}{4 \pi} \frac{I d l \sin \theta}{r^{2}}\)
सीधे भाग में प्रवाहित धारा के कारण \(\overrightarrow{d l}\) और \(\vec{r}\) के बीच का कोण θ = 0° या 180° होगा।
अतः sinθ = sin 0° = sin 180° = 0
अतः सीधे भागों में प्रवाहित धारा के कारण केंद्र P पर चुंबकीय क्षेत्र शून्य होगा।
अर्धवृत्ताकार चाप के कारण केंद्र P पर चुंबकीय क्षेत्र

B =\(\frac{\mu_{0} I}{2 r} \times \frac{1}{2}\) = \(\frac{\mu_{0} l}{4 r}\)
दिया है- I = 12 ऐम्पियर, r = 2 सेमी = 2 × 10^-2 मीटर
मान रखने पर,
B = \(\frac{4 \pi \times 10^{-7} \times 12}{4 \times 2 \times 10^{-2}}\)
= \(\frac{3 \cdot 14 \times 12 \times 10^{-7}}{2 \times 10^{-2}}\) = 1.88 × 10⁴ टेस्ला
= 1.9 × 10^-4 टेस्ला ।
दाएँ हाथ के नियमानुसार चित्र (a) की भाँति तार को मोड़ने पर केंद्र पर चुंबकीय क्षेत्र की दिशा कागज के तल के लंबवत ऊपर की ओर होगी।
यदि तार को चित्र (b) के अनुसार मोड़ दिया जाये तो चुंबकीय क्षेत्र का परिमाण वही रहेगा किंतु उसकी दिशा कागज के तल के लंबवत नीचे की ओर होगी।

प्रश्न 6.
तार की एक वृत्ताकार कुंडली में 100 फेरे हैं, प्रत्येक की त्रिज्या 8.0 cm है और इनमें 0.40A विद्युत धारा प्रवाहित हो रही है। कुंडली के केंद्र पर चुंबकीय क्षेत्र का परिमाण क्या है ?
उत्तर-
हल-दिया है-N=100; r= 8.0 cm = 8 × 10^-2m; I = 0.40A
सूत्र- B = \(\frac{\mu_{0} N I}{2 r}\) = \(\frac{4 \pi \times 10^{-7} \times 100 \times 0.40}{2 \times 8 \times 10^{-2}} \)
= \(\frac{4 \times 3 \cdot 14 \times 10^{-7} \times 100 \times 0 \cdot 40}{2 \times 8 \times 10^{-2}}\)
= 3.14 × 10^-5T.

प्रश्न 7.
एक लंबे, सीधे तार में 35A विद्युत धारा प्रवाहित हो रही है। तार से 20 cm दूरी पर स्थित किसी बिंदु पर चुंबकीय क्षेत्र का परिमाण क्या है ?
उत्तर-
हल-दिया है-I = 35A; r= 20 cm = 20 × 10^-2m
सूत्र B = \(\frac{\mu_{0} I}{2 \pi r}\) = \(\frac{4 \pi \times 10^{-7} \times 35}{2 \pi \times 20 \times 10^{-2}}\)
= 3.5 × 10^-5T.

प्रश्न 8.
क्षैतिज तल में रखे एक लंबे सीधे तार में 50A विद्युत धारा उत्तर से दक्षिण की ओर प्रवाहित हो रही है। तार के पूर्व में 2.5m दूरी पर स्थित किसी बिंदु पर चुंबकीय क्षेत्र \(\overrightarrow{\boldsymbol{B}}\) का परिमाण और उसकी दिशा ज्ञात कीजिए।
उत्तर-
हल-दिया है-I = 50A; r = 2.5 m
सूत्र- B= \(\frac{\mu_{0} I}{2 \pi r}\) = \(\frac{4 \pi \times 10^{-7} \times 50}{2 \pi \times 2 \cdot 5}\)
=4 × 10^-6T.
दाएँ हाथ के नियम के अनुसार इसकी दिशा ऊर्ध्वाधर ऊपर की ओर होगी।

प्रश्न 9.
व्योमस्थ खींचे क्षैतिज बिजली के तार में 90A विद्युत धारा पूर्व से पश्चिम की ओर प्रवाहित हो रही है। तार के 1.5 m नीचे विद्युत धारा के कारण उत्पन्न चुंबकीय क्षेत्र का परिमाण और उसकी दिशा क्या है ?
उत्तर-
हल-दिया है- I = 90 A; r = 1.5 m
सूत्र- B= \(\frac{\mu_{0} I}{2 \pi r}\) = \(\frac{4 \pi \times 10^{-7} \times 90}{2 \pi \times 1.5}\)
= 12 × 10^-6
= 1.2 × 10^-5T
दाएँ हाथ के नियम के अनुसार इसकी दिशा दक्षिण की ओर होगी।

प्रश्न 10.
एक तार जिसमें 8A विद्युत धारा प्रवाहित हो रही है। 0.15T के एकसमान चुंबकीय क्षेत्र में, क्षेत्र से 30° का कोण बनाते हुए रखा है। इसकी एकांक लंबाई पर लगने वाले बल का परिमाण और इसकी दिशा क्या है ?
उत्तर-
हल– दिया है-I=8A; B= 0.15T; θ= 30°
सूत्र- F = IlB sinθ
या f=\(\frac{F}{l} \) = IBsin 30°
=8 × 0.15 sin30°=8 × 0.15 × \(\frac{1}{2}\)
=0.60N/m
इसकी दिशा \(\vec{l}\) और \(\vec{B}\) दोनों के लंबवत होगी।

प्रश्न 11.
एक-दूसरे से 4.0 cm की दूरी पर रखे दो लंबे, सीधे, समांतर तारों A एवं B से क्रमशः 8.0A एवं 5-0A की विद्युत धाराएँ एक ही दिशा में प्रवाहित हो रही हैं। तार A के 10 cm खंड पर बल का आकलन कीजिए।
उत्तर-
हल– दिया है- d= 4.0 cm = 4.0 x 10^-2m; I₁ = 8A; I₂ =5A; l = 10 cm = 10 x 10^-2m;
सूत्र- F = \(\frac{\mu_{0} I_{1} I_{2}}{2 \pi d} l\)
= \(\frac{4 \pi \times 10^{-7} \times 8 \times 5 \times 10 \times 10^{-2}}{2 \pi \times 4 \times 10^{-2}}\)
=20 × 10^-6 = 2.0 × 10^-5N
यह आकर्षण बल होगा। अत: इसकी दिशा A के लंबवत B की ओर होगी।

प्रश्न 12.
पास-पास फेरों वाली एक परिनालिका 80cm लंबी है और इसमें 5 परतें हैं जिनमें से प्रत्येक में 400 फेरे हैं। परिनालिका का व्यास 1.8 cm है। यदि इसमें 8.0A विद्युत धारा प्रवाहित हो रही है, तो परिनालिका के भीतर केंद्र के पास चुंबकीय क्षेत्र \(\overrightarrow{\boldsymbol{B}}\) के परिमाण परिकलित कीजिए।
उत्तर-
हल-दिया है- l = 80 cm = 80 x 10^-2 m; N = 400; परतों की संख्या = 5; l = 8.0A
∴ प्रति एकांक लंबाई में फेरों की संख्या
n = \(\frac{400 \times 5}{80 \times 10^{-2}}\)

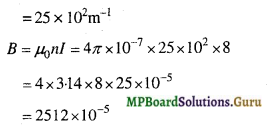
= 2.5 × 10^-2 T.

वस्तुनिष्ठ प्रश्न

1. सही विकल्प चुनकर लिखिए

प्रश्न 1.
एक गतिमान आवेश उत्पन्न करता है
(a) केवल स्थिर विद्युत्-क्षेत्र
(b) केवल चुम्बकीय क्षेत्र
(c) स्थिर विद्युत्-क्षेत्र और चुम्बकीय क्षेत्र दोनों
(d) इनमें से कोई नहीं।
उत्तर-
(c) स्थिर विद्युत्-क्षेत्र और चुम्बकीय क्षेत्र दोनों

प्रश्न 2.
एक ऊर्ध्वाधर तल में बहने वाली धारा क्षैतिज पृष्ठ के लम्बवत् अन्दर की ओर जाने वाली है। यदि एक क्षैतिज चुम्बकीय क्षेत्र दाहिनी ओर से कार्यरत है तब तार के ऊपर लगने वाला बल क्षैतिज तल में
(a) दाहिनी ओर होगा
(b) बायीं ओर होगा
(c) हमारी ओर होगा
(d) हमसे विपरीत दिशा में होगा।
उत्तर-
(c) हमारी ओर होगा

प्रश्न 3.
एक इलेक्ट्रॉन उत्तर की ओर गतिमान है। यह ऊर्ध्वाधर ऊपर की ओर एक बल अनुभव करता है। इलेक्ट्रॉन की स्थिति पर चुम्बकीय क्षेत्र की दिशा होगी
(a) पूर्व
(b) पश्चिम
(c) उत्तर
(d) दक्षिण।
उत्तर-
(a) पूर्व

प्रश्न 4.
धारावाही चालक के कारण उत्पन्न क्षेत्र की दिशा निम्न नियम से ज्ञात की जाती है
(a) फ्लेमिंग के बायें हाथ का नियम
(b) फ्लेमिंग के दायें हाथ का नियम
(c) ऐम्पियर के तैरने का नियम
(d) इनमें से कोई नहीं।
उत्तर-
(c) ऐम्पियर के तैरने का नियम

प्रश्न 5.
प्रोटॉन को चुम्बकीय क्षेत्र के लम्बवत् प्रक्षेपित किया जाता है
(a) प्रोटॉन की गति पर चुम्बकीय क्षेत्र का प्रभाव नहीं होगा
(b) प्रोटॉन उसी दिशा में गति जारी रखेगा किन्तु संवेग प्राप्त करेगा
(c) प्रोटॉन उसी दिशा में गति जारी रखेगा किन्तु संवेग प्राप्त नहीं करेगा
(d) वह वृत्त के चाप में मुड़ जायेगा।
उत्तर-
(d) वह वृत्त के चाप में मुड़ जायेगा।

प्रश्न 6.
कुछ दूरी पर स्थित दो समान्तर तारों में I₁ और I₂ धारा एक ही दिशा में प्रवाहित हो रही है। दोनों तार
(a) एक-दूसरे को आकर्षित करेंगे
(b) एक-दूसरे को प्रतिकर्षित करेंगे
(c) एक-दूसरे को न तो आकर्षित करेंगे और न ही प्रतिकर्षित
(d) इनमें से कोई नहीं।
उत्तर-
(a) एक-दूसरे को आकर्षित करेंगे

प्रश्न 7.
एक आवेशित कण चुम्बकीय क्षेत्र की दिशा में गति कर रहा है। कण पर लगने वाला चुम्बकीय बल
(a) उसके वेग की दिशा में है
(b) उसके वेग की विपरीत दिशा में है
(c) उसके वेग के लम्बवत् है
(d) शून्य है।
उत्तर-
(d) शून्य है।

प्रश्न 8.
एक इलेक्ट्रॉन अनुप्रस्थ चुम्बकीय क्षेत्र B में v चाल से त्रिज्या के वृत्ताकार पथ पर गति कर रहा है। इसके लिए \(\frac{e}{m}\) होगा –
(a) \(\frac{v}{B r}\)
(b) \(\frac{\mathrm{B}}{r v}\)
(c) Bvr
(d) \(\frac{v r}{B}\)
उत्तर-
(a) \(\frac{v}{B r}\)

प्रश्न 9.
धारावाही वृत्तीय कुण्डली के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र होता है
(a) कुण्डली के तल में
(b) कुण्डली के तल के लम्बवत्
(c) कुण्डली के तल से 45° पर
(d) कुण्डली के तल से 135° पर ।
उत्तर-
(b) कुण्डली के तल के लम्बवत्

प्रश्न 10.
एक वृत्तीय कुण्डली में बहने वाली धारा को दुगुना करने तथा इसमें फेरों की संख्या आधी करने पर इसके केन्द्र पर चुम्बकीय क्षेत्र का मान होगा
(a) दुगुना
(b) आधा
(c) अपरिवर्तित
(d) चौगुना।
उत्तर-
(c) अपरिवर्तित

प्रश्न 11.
चल कुण्डली धारामापी में त्रिज्यीय क्षेत्र बनाने के लिए
(a) कुण्डली में ,फेरों की संख्या बढ़ाते हैं
(b) चुम्बक नाल चुम्बक के रूप में लेते हैं
(c) ध्रुव अवतलाकार काटे जाते हैं
(d) कुण्डली को ऐल्युमिनियम फ्रेम पर लपेटते हैं।
उत्तर-
(c) ध्रुव अवतलाकार काटे जाते हैं

प्रश्न 12.
एक अमीटर की कुण्डली का प्रतिरोध 50 ओम है। उसके पैमाने के विस्तार को 10 गुना करने के लिए कितने प्रतिरोध के शण्ट की आवश्यकता होगी
(a) 500 ओम
(b) 5 ओम
(c) ओम
(d) ओम ।
उत्तर-
(d) ओम ।

प्रश्न 13.
जब कोई विद्युत् आवेशित कण एकसमान चुम्बकीय क्षेत्र में प्रवेश करता है तो इसकी गतिज ऊर्जा
(a) नियत रहती है
(b) बढ़ती है
(c) घटती है
(d) शून्य हो जाती है।
उत्तर-
(a) नियत रहती है

प्रश्न 14.
समान गतिज ऊर्जा का एक इलेक्ट्रॉन और प्रोटॉन चुम्बकीय क्षेत्र में लम्बवत् प्रवेश करते हैं। निम्न में क्या सत्य है
(a) इलेक्ट्रॉन का पथ कम वक्रता का है।
(b) प्रोटॉन का पथ कम वक्रता का है।
(c) दोनों के पथ समान वक्रता के हैं।
(d) दोनों सीधी रेखा पथ पर चलते हैं।
उत्तर-
(b) प्रोटॉन का पथ कम वक्रता का है।

प्रश्न 15.
एक धारामापी का प्रतिरोध 90 ओम है। यदि धारामापी में मुख्य धारा का केवल 10% भाग जाना है तो प्रतिरोध को किस प्रकार उपयोग में लाना होगा और इसका मान कितना होगा
(a) श्रेणी क्रम में 10 ओम
(b) समान्तर क्रम में 10 ओम
(c) श्रेणी क्रम में 810 ओम
(d) समान्तर क्रम में 810 ओम।
उत्तर-
(b) समान्तर क्रम में 10 ओम

प्रश्न 16.
धारामापी को प्रबल विद्युत् धारा से होने वाली संभावित क्षतियों से बचाने के लिए उसकी कुण्डली के साथ जोड़ते हैं
(a) कम प्रतिरोधक का तार श्रेणी क्रम में
(b) कम प्रतिरोध का तार समांतर क्रम में
(c) उच्च प्रतिरोध का तार श्रेणी क्रम में
(d) उच्च प्रतिरोध का तार समांतर क्रम में।
उत्तर-
(b) कम प्रतिरोध का तार समांतर क्रम में

प्रश्न 17.
धारामापी को वोल्टमीटर में बदलने के लिए उसकी कुंडली के साथ जोड़ते हैं
(a) उच्च प्रतिरोध का तार श्रेणी क्रम में
(b) कम प्रतिरोध का तार समांतर क्रम में
(c) उच्च प्रतिरोध का तार समांतर क्रम में
(d) कम प्रतिरोध का तार श्रेणी क्रम में।
उत्तर-
(a) उच्च प्रतिरोध का तार श्रेणी क्रम में

प्रश्न 18.
धारामापी को अमीटर में बदलने के लिए उसकी कुंडली के साथ जोड़ते हैं
(a) उच्च प्रतिरोध का तार श्रेणी क्रम में
(b) कम प्रतिरोध का तार समांतर क्रम में
(c) उच्च प्रतिरोध का तार समांतर क्रम में
(d) कम प्रतिरोध का तार श्रेणी क्रम में।
उत्तर-
(b) कम प्रतिरोध का तार समांतर क्रम में

प्रश्न 19.
एक बीटा (B) कण चुम्बकीय क्षेत्र के समानांतर गति कर रहा है, तो उस पर लगने वाला बल होगा
(a) शून्य
(b) 0.1 न्यूटन
(c) 1 न्यूटन
(d) इनमें से कोई नहीं।
उत्तर-
(a) शून्य

प्रश्न 20.
एक अल्फा (a) कण चुम्बकीय क्षेत्र के समानांतर गति कर रहा है, तो उस पर लगने वाला बल होगा
(a) शून्य
(b) 0.2 न्यूटन
(c) 2 न्यूटन
(d) इनमें से कोई नहीं।
उत्तर-
(a) शून्य.

2. रिक्त स्थानों की पूर्ति कीजिए

1. विद्युत् धारा के चुम्बकीय प्रभाव की खोज …………. ने की थी।
उत्तर-
ओर्टेड

2. बायो-सेवर्ट के नियमानुसार धारावाही चालक के अल्पांश के कारण उत्पन्न चुम्बकीय क्षेत्र उसके निकट किसी बिन्दु पर, धारा के …………. तथा दूरी के …………. होती है।
उत्तर-
अनुक्रमानुपाती, वर्ग के व्युत्क्रमानुपाती

3. बायो-सेवर्ट के नियम को …………. का नियम भी कहते हैं।
उत्तर-
लाप्लास

4. धारावाही चालक के कारण उत्पन्न चुम्बकीय क्षेत्र की दिशा मैक्सवेल के …………. के नियम या …………. हाथ की हथेली के नियम क्र. 1 से दी जाती है।
उत्तर-
दक्षिणावर्ती पेंच, दाहिने

5. धारावाही वृत्तीय कुण्डली के केन्द्र में उत्पन्न चुम्बकीय क्षेत्र की तीव्रता कुण्डली की त्रिज्या के ………….. तथा फेरों की संख्या के …………. होती है।
उत्तर-
व्युत्क्रमानुपाती, अनुक्रमानुपाती

6. किसी चुम्बकीय क्षेत्र में गतिमान आवेश पर लगने वाले बल को …………. बल कहते हैं।
उत्तर-
लॉरेंज

7. ………… का उपयोग आवेशित कणों को त्वरित करने में किया जाता है।
उत्तर-
सायक्लोट्रॉन

8. धारावाही परिनालिका के अंदर चुम्बकीय क्षेत्र की तीव्रता उसके अक्ष के ………… होती है।
उत्तर-
अनुदिश

9. दो समान्तर धारावाही चालकों में यदि एक ही दिशा में धारा प्रवाहित होता है तो उनके मध्य ………….बल तथा विपरीत दिशा में धारा प्रवाहित होने पर …………. बल लगता है।
उत्तर-
आकर्षण, प्रतिकर्षण

10. स्पर्शज्या धारामापी …………. नियम पर आधारित है।
उत्तर-
स्पर्शज्या

11. धारामापी को अमीटर में परिवर्तित करने के लिये धारामापी के समान्तर क्रम में ……….. लगाया जाता है।
उत्तर-
निम्न प्रतिरोध

12. आदर्श अमीटर का प्रतिरोध ………… होता है।
उत्तर-
शून्य

13. धारामापी को वोल्टमीटर में परिवर्तित करने के लिये धारामापी के …………. क्रम में …………. मान ………….. का प्रतिरोध लगाया जाता है।
उत्तर-
श्रेणी, उच्च

14. आदर्श वोल्टमीटर का प्रतिरोध ………… होता है।
उत्तर-
अनंत

15. अमीटर को विद्युत परिपथ में ………… क्रम में जोड़ा जाता है।
उत्तर-
श्रेणी

16. वोल्टमीटर को विद्युत् परिपथ में ……….. क्रम में जोड़ा जाता है।
उत्तर-
समान्तर

17. लॉरेन्ज बल की दिशा …………. के …………. नियम से दी जाती है।
उत्तर-
फ्लेमिंग, बायें हाथ के

18. शण्ट लगाने से अमीटर की सुग्राहिता …………. हो जाती है।
उत्तर-
कम

19. वृत्तीय धारावाही कुण्डली एक …………. के समतुल्य होती है।
उत्तर-
चुम्बक।

3. उचित संबंध जोडिए

स्तम्भ ‘अ’	स्तम्भ ‘ब’
1. बायो-सेवर्ट का नियम	(a) B = \(\frac{\mu_{0}}{4 \pi}\).\(\frac{2 \pi n \mathrm{I}}{r}\)
2. लम्बे ऋजुरेखीय धारावाही चालक के समीप चुम्बकीय क्षेत्र	(b) B = μ0nI
3. धारावाही वृत्तीय कुण्डली के केन्द्र में उत्पन्न चुम्बकीय क्षेत्र	(c) \(\overrightarrow{\mathrm{F}}\) = q\((\vec{v} \times \overrightarrow{\mathrm{B}})\)
4. परिनालिका के अक्ष में उत्पन्न चुम्बकीय क्षेत्र	(d) dB = \(\frac{\mu_{0}}{4 \pi}\).\(\frac{\mathrm{I} d \sin \theta}{r^{2}}\)
5. लॉरेंज बल	(e) B= \(\frac{\mu_{0}}{4 \pi}\) .\(\frac{2 \mathrm{I}}{d}\)

उत्तर-
1.  (d) dB = \(\frac{\mu_{0}}{4 \pi}\).\(\frac{\mathrm{I} d \sin \theta}{r^{2}}\)
2.  (e) B= \(\frac{\mu_{0}}{4 \pi}\) .\(\frac{2 \mathrm{I}}{d}\)
3. (a) B = \(\frac{\mu_{0}}{4 \pi}\).\(\frac{2 \pi n \mathrm{I}}{r}\)
4. (b) B = μ₀nI
5. (c) \(\overrightarrow{\mathrm{F}}\) = q\((\vec{v} \times \overrightarrow{\mathrm{B}})\).