MP Board Class 12th Physics Important Questions Chapter 3 Current Electricity

MP Board Class 12th Physics Important Questions Chapter 3 Current Electricity

Current Electricity Important Questions

Current Electricity Objective Type Questions

Question 1.
Choose the correct answer of the following:

Question 1.
The flow of current through a conduction is due to:
(a) Protons
(b) Positive ions
(c) Free electrons
(d) Positive and negative ions.
Answer:
(c) Free electrons

Question 2.
The specific resistance of a wire depends upon:
(a) Length
(b) Diameter
(c) Mass
(d) Material.
Answer:
(b) Diameter

Question 3.
A wire is stretched redouble its length. Its resistance will be:
(a) Halved
(b) Doubled
(c) One fourth
(d) Four times.
Answer:
(d) Four times.

Question 4.
The unit of specific resistance is :
(a) Ohm
(b) Ohm^-1
(c) Ohm meter
(d) Ohm^-1
Answer:
(c) Ohm meter

Question 5.
Which of the following is an oh-mic resistance:
(a) Junction transistor
(b) Transistor
(c) LED
(d) Copper wire.
Answer:
(d) Copper wire.

Question 6.
On increasing temperature the resistance of the which of the following decreases :
(a) Semiconductor
(b) Metal
(c) Electrolyte
(d) Alloy.
Answer:
(a) Semiconductor

Question 7.
The conductance of super conductor is :
(a) Infinite
(b) Very high
(c) Very low
(d) Zero.
Answer:
(a) Infinite

Question 8.
In the series combination of two resistance which quantity remains same :
(a) Only potential difference
(b) Only current
(c) Current and potential difference both
(d) Neither current nor potential difference.
Answer:
(b) Only current

Question 9.
Electric cell is source of:
(a) Electrons
(b) Electrical energy
(c) Electric charge
(d) Electric current.
Answer:
(b) Electrical energy

Question 10.
The e.m.f. of a cell depends upon:
(a) Quantity of electrolyte filled in it
(b) Distance between the electrodes
(c) Size of electrodes
(d) Nature of electrolyte and electrodes.
Answer:
(d) Nature of electrolyte and electrodes.

Question 11.
Three cells each having e.m.f. E and internal resistance r are joined in series. One cell by mistake is joined in reverse order. The resultant e.m.f. and internal resistance will be:
(a) 3E, 3r
(b) E,3r
(c) E, r
(d) 3E,r
Answer:
(b) E,3r

Question 12.
The internal resistance of a cell can be decreased by :
(a) Decreasing the size of electrodes
(b) Increasing the distance between electrodes
(c) Decreasing the distance between electrodes
(d) None of these.
Answer:
(c) Decreasing the distance between electrodes

Question 13.
Two cells of e.m.f. and internal resistance E₁r₁ and E₂, r₂ respectively are joined in parallel. Their equivalent e.m.f. will be:
(a) E₁ + E₂
(b) E₁ – E₂
(c) \(\frac{\mathrm{E}_{1} r_{2}+\mathrm{E}_{2} r}{r_{1}+r_{2}}\)

(d) \(\frac{\mathrm{E}_{1}+\mathrm{E}_{2}}{r_{1}+r_{2}} \times r_{1} \cdot r_{2}\)
Answer:

(c) \(\frac{\mathrm{E}_{1} r_{2}+\mathrm{E}_{2} r}{r_{1}+r_{2}}\)

Question 14.
Potentiometer measures:
(a) Terminal voltage of cell
(b) Current in circuit
(c) e.m.f. of cell
(d) None of these.
Answer:
(c) e.m.f. of cell

Question 15.
In the null deflection position:
(a) No current flows through the galvanometer
(b) Current flows due to primary circuit through the galvanometer
(c) Current flows through galvanometer due to secondary circuit
(d) Nothing can be said.
Answer:
(a) No current flows through the galvanometer

Question 16.
The SI unit of the potential gradient is:
(a) ohm/cm
(b) volt
(c) volt cm
(d) volt/cm.
Answer:
(d) volt/cm.

Question 17.
To increase the sensitivity of potentiometer:
(a) The potential difference across its wire should be high
(b) The length of its wire should be less
(c) The current through the wire should be high
(d) potential difference across its wire should be low and length of wire should be large.
Answer:
(d) potential difference across its wire should be low and length of wire should be large.

Question 18.
In the balance condition of potentiometer its resistance is :
(a) Zero
(b) Infinite
(c) Very small
(d) Very high.
Answer:
(d) Very high.

Question 2.
Fill in the blanks:

1. According to ……….. law, a if the physical conditions of a conductor remains unchanged then current flowing through it is directly proportional to the applied potential difference.
2. On increasing the length of a conductor its resistance ………..
3. On decreasing the area of cross-section of a conductor its resistance ………..
4. On increasing the temperature of a metallic conductor its resistance ………..
5. KirchhofFs first law is in accordance with the law of conservation of ………..
6. In series grouping of resistors the resistance but in parallel grouping the resistance ………..
7. With increase in length of potentiometer its sensitivity ………..
8. Meter bridge works on the principle of ………..
9. The specific resistance of alloys is ……….. and temperature coefficient of resistance is ………..
10. The Kirchhoff’s first law is in accordance with the law of conservation of ……….. while the second law is in accordance with law of conservation of ………..
11. On increasing the distance between electrodes of a cell, its internal resistance ……….. but on increasing area its internal resistance ………..
12. The phenomenon in which at low temperature the resistivity of a substance becomes zero is celled ………..
13. In Ohm’s law the V-I graph is a ………..

Answers:

1. Ohm’s
2. Increases
3. Increases
4. Increases
5. Charge
6. Increases, decreases,
7. Increases
8. Wheatstone bridge
9. High, low
10. Charge, energy
11. Increases, decreases
12. Super conductivity
13. Straight line.

Question 3.
Match the Column:

Answer:

1. (e) Metre Bridge
2. (c) Law of conservation of charge
3. (b) Ohmic conductor
4. (a) Law of energy conservation
5. (d) Non-ohmic conductor

Answers:

1. (e) coulomb/sec. (or ampere).
2. (d) ampere/metre²
3. (b) joule/coulombx ampere
4. (c) ohm x meter
5. (a) ohm^-1

Answers:

1. (e) I²Rt
2. (a) ohm
3. (b) volt
4. (c) Electrical energy
5. (d) VI

Answer:

1. (c) Potential difference
2. (e) e.m.f.
3. (b) Vector quantity
4. (a) l₁/l₂
5. (d) \(\mathrm{R}\left(\frac{l_{1}}{l_{2}}-1\right)\)

Question 4.
Write the answer in one word / sentence:

1. What is the direction of electric current ?
2. What is the unit of specific resistance ?
3. Kirchhoffs first law is based upon which law ?
4. Kirchhoffs second law is based upon which law ?
5. On which principle does f&etre bridge works ?
6. Does Kirchhoffs law can be applied for both a.c. and d.c. currents ?
7. In a carbon resistance, there is green, violet, red and silver strip’s. What will be the resultant resistance.
8. What is the relation between 1 kWh and joule.
9. When the potentiometer is in equilibrium, what will be its resistance ?
10. The algebraic sum of current at a point is zero. Then what will be that point ?

Answer:

1. Opposite to flow of electrons,
2. Unit is ohm x meter
3. Laws of conservation of charges
4. Laws of conservation of energy
5. Wheatstone bridge
6. Yes
7. 57 x 10² ± 10% ohm
8. 1 kWh = 3.6 x 106 joule
9. Infinity
10. Junction point.

Current Electricity Very Short Answer Type Questions

Question 1.
To flow current in a conducting wire, how much charges is present in it ?
Answer:
On flowing current through the conducting wire, charges becomes zero.

Question 2.
Why Meter bridge is known by these name ?
Answer:
Because in Meter bridge, a wire of one meter length is used.

Question 3.
Two bulb are marked as 25 W and 100 W. Whose resistance will be more ?
Answer:
R ∝ \(\frac {1}{V}\), Resistance of 25 W bulb will be more.

Question 4.
What do you mean by electric power. Write its unit ?
Answer:
In any electrical circuit the rate of energy decay is called as power. Its unit is watt.

Question 5.
On which factor relaxation time depend on ?
Answer:
It depends on nature of the material of the conductor.

Question 6.
Why there is internal resistance in a cell ?
Answer:
Because, inside the cell, the motion of ions get obstacled by the collision of electrolytes molecules.

Question 7.
Why wire of Meter bridge is not made of copper wire ?
Answer:
Since the resistance of copper wire is very less and its temperature coefficient is more, therefore it is not used in Meter bridge.

Current Electricity Short Answer Type Questions

Question 1.
What is current ? Write its unit
Answer:
The electric current is defined as the rate of flow of charge through any section of a
Electric current = \(\frac {Total charge flowing}{ Time taken }\)
l = \(\frac {q}{ t}\) The SI unit of electric current is ampere (A).

Question 2.
Is electric current a scalar or a vector quantity ? Give reason.
Answer:
Electric current is a scalar quantity. This is because laws of ordinary algebra are used to add electric current and laws of vector addition are not applied for the addition of electric current.

Question 3.
Define current density. Is it scalar or vector ? Write its unit.
Answer:
Current density at a point in a conductor is defined as the amount of current flowing per unit area of the conductor held perpendicular to the flow of current.
Current density J = \(\frac {Current (l)}{ Area (S)}\) (or) \(\frac {l}{ S}\)
Current density is a vector quantity. The SI unit of current density is ampere / meter².

Question 4.
What is drift velocity ? What is its value ?
Answer:
Drift velocity is defined as the average velocity with which the velocity free electrons with which they get drifted towards the positive terminal of the conductor under the influence of the external electric field. Its value is 10^-5ms^-1

Question 5.
Is Ohm’s law applicable to all conductors ? Write conditions for its application
Or
Write the condition or under which Ohm’s law is not obeyed.
Answer:
No, Ohm’s law is not applicable for non – ohmic conductors, e.g., semiconductor diode, discharge tube, etc. It is valid only when there is no change in physical conditions of conductor i.e., temperature, length or mechanical strain etc.

Question 6.
Define specific resistance or resistivity. Write its unit and dimensional formula.
Answer:
Specific resistance or resistivity is numerically equal to the resistance offered by a conductor of unit length and unit cross-sectional area. Its unit is ohm – meter. It depends upon temperature. a’ ‘ The dimensional formula of specific resistance is [ML³T³A^-2].

Question 7.
If you are given two wires of same material, having same length but different diameters, then which wire will have higher resistance and which will have high specific resistance ?
Answer:
The thin wire (having less diameter) will have higher resistance than that of thicker one as R ∝ \(\frac { 1 }{ A }\) Both wires will have same specific resistance as they are made of same material and specific resistance is characteristic of the material of wire.

Question 8.
It is easier to start motor car during summer rather than in winter. Why ?
Answer:
The internal resistance of the battery during summer is less as compared to winter, therefore more current can be drawn from the battery.

Question 9.
When a high power heater is connected to mains, bulbs become dim. Why ?
Answer:
All electrical appliances are connected in parallel at home, therefore when power heater is used, very high current passes through it. So, potential difference falls on wires connected through mains (V = E – lr), which results in decreasing intensity of bulbs used in circuit.

Question 10.
What do you measure by meter bridge ? When is its sensitivity maximum ?
Answer:
Resistances are measured by meter bridge. Sensitivity of meter bridge is maximum when the null point is obtained at the center of wire. Moreover, all the resistances must be of same order.

Question 11.
What is the wire of meter bridge made up of ?
Answer:
The wire of meter bridge is made of manganin or constantan because it has low temperature coefficient of resistance and high specific resistance.

Question 12.
How can the sensitivity of potentiometer be increased ?
Answer:
The sensitivity of the potentiometer will be more if the potential gradient is less. For this, V should be less but more than the emf of E. The length of potentiometer should be large.

Question 13.
Write two possible reasons for obtaining deflection on one side in the experiment of potentiometer.
Answer:
The two possible reasons are as follows:

• If the emf of secondary cell in primary circuit is less than the emf of primary cell in the secondary circuit.
• If positive terminals of all the cells are not connected to the same point.

Question 14.
What do you understand by potential gradient of a potentiometer ? Give its unit
Answer:

• Fall in potential per unit length is called potential gradient. If the length of wire be / and potential difference across the wire is v, then
• Potential gradient, K =\(\frac {V}{l}\) Its unit is volt / m.

Question 15.
The potential gradient of potentiometer wire is doubled, what will happen to its null point ?
Answer:
Let emf of cell E is balanced at the length of –
E = Kl = l = \(\frac {E}{ K}\) = l ∝ \(\frac {1}{ K}\)
Hence, the null point will be at the half of the length.

Question 16.
Why the length of wire in potentiometer is more ?
Answer:
For greater sensitivity, the length of null point should be greater, for which the potential gradient should be smaller.
Potential gradient, K =\(\frac {V}{ l}\) To decrease K the value of l should be greater and F should be smaller. But, the value of V can be decreased up to a certain limit, hence the length is increased sufficiently.

Question 17.
Prove that potentiometer is an ideal voltmeter.
Answer:
When the potential difference between two points is measured by the voltmeter, then same current passes through the voltmeter, hence it measures little less than actual potential difference. But, when potentiometer measures the potential difference between two points, no current flows through it. Hence, it measures the accurate potential difference.

Question 18.
A carbon resistance has bands blue, red and green respectively. What is its resistance ?
Answer:

.’. The value of carbon resistance is 62 x 105 ohm with tolerance ± 20% .

Question 19.
A carbon resistance has bands blue, green and red respectively. Write its resistance.
Answer:

The value of carbon resistance is 65 x 102 ohm with tolerance ± 20% .

Question 20.
A carbon resistance has bands red, blue and green. What is its resistance ?
Answer:

The value of carbon resistance is 26 x 105 ohm with tolerance ±20% .

Question 21.
In high tension battery internal resistance should be high. Why ?
Answer:
If high tension battery is used in a circuit having low external resistance, current may go beyond its safety limit. If internal resistance of the battery is high, then current cannot go beyond its safety limit. So, internal resistance of high tension battery must be high.

Question 22.
What is cause of end error in a meter bridge ?
Answer:
The end error in meter bridge is due to following reasons:
The zero mark of the scale provided along the wire may not start from the position where the bridge wire leaves the copper strip and 100 cm mark of the scale may not end at the position where the wire touches the copper strip. The resistance of the copper wire and metal strip of meter bridge has not been taken in account.

Question 23.
What is Ohm’s law ? On what factors does the resistance of a conductor depend upon ?
Answer:
If all the physical conditions of any conductor as length, temperature, etc. remain constant, then the current which flows through it is proportional to the potential difference applied across the ends of the conductor. If I is the current in conductor and V is the potential difference, then
V ∝ l = V=RI
Where, R is a constant, called resistance of conductor.
For factors affecting resistance of conductor:

• Length: The resistance of conductor is directly proportional to the length of the conductor i.e., R ∝ l
• Area of cross – section: The resistance of a conductor is inversely proportional to the area of cross – section of the conductor i.e., R ∝ \(\frac{l}{A}\)
• Temperature: Increase in temperature, increases the resistance.

Combining above two laws, we get,
R ∝ \(\frac{l}{A}\)
R = p \(\frac{l}{A}\)
Where, p= a constant, called specific resistance of the material of the conductor.
Specific resistance:
We have,
R = p \(\frac{l}{A}\)
Let l = 1 And A = l, then
R = P

Thus, the specific resistance of a material is defined by the resistance of unit length and unit area of cross-section of that material.
Unit: Now, p = \(\frac{R.A}{l}\)
= \(\frac{Unit of R x Unit of A}{Unit of l}\)
= \(\frac{\mathrm{ohm} \times \mathrm{m}^{2}}{\mathrm{m}}\) = Ohm x m = Ω x m

Question 24.
What are the possible errors of a meter bridge and how can they be removed ?
Answer:
The possible errors and their removal methods are:
1. It might happen that the wire is not uniform. To remove this error, balance point should be obtained at the-middle.

2. During’the experiment, it is assumed that the resistance of L shaped plates are negligible, but actually it is not so. The error created due to this is called end error. To remove this error, the resistance box and the unknown resistance must be interchanged and then the mean reading should be taken.

3. If the jockey is pressed for a long period of time, then it gets heated and its resistance changes. Hence, jockey must not be pressed for a long interval.

Question 25.
Prove Ohm’s law on the basis of free electron theory.
or
Determine the formula for specific resistance in terms of free electron density and relaxation time.
Answer:
Consider a conductor of length l, area of cross-section A having ‘n’ No. of free electron per unit volume. If potential difference V is applied between its opposite ends then,
\(\frac { V }{ l }\)
Force experienced by each free electron will be
F = eE or F = \(\frac { eV }{ l }\)
The acceleration produced on the electron of mass m is
a = \(\frac { F }{ m}\) = \(\frac { eV }{ ml }\)
If the time interval between two successive collisions (relaxation time) is r then drift velocity is
V_d = \(\frac {eEτ }{ m }\)
= \(\frac {eVτ }{ ml }\)
But cuurent l = neAv_d
l = neA\(\left(\frac{e V \tau}{m l}\right)=\frac{n e^{2} \tau}{m} \frac{A}{l}V\)
\(\frac { V }{ l }\) = \(\frac{m}{n e^{2} \tau} \cdot \frac{l}{A}\)
If temperature remains constant, then all terms on R.H.S. will be constant, so
\(\frac { V }{ l }\) = R
This is Ohm’s law. Where R is constant called resistance.
R = \(\frac{m}{n e^{2} \tau} \cdot \frac{l}{A}\) ……….(1)
But resistance is directly proportional to length / and inversely proportional to area of cross-section A of conductor
R ∝ \(\frac { l }{A }\)
R = p\(\frac { l }{A }\) ………..(2)
From eqns. (1) and (2),
p = \(\frac{m}{n e^{2} \tau}\)

Question 26.
Obtain a relationship between current and drift velocity.
Answer:
Consider a conductor of length /and area of cross-section A. Let n be the number of electrons per unit volume.
Volume of conductor = Al
Total number of electrons = nAl.
Total charge of conductor, Q = nAle.
The conductor is now joined to a cell of potential difference V.
So, the electrons get drifted towards the positive terminal of the cell. Let the drift velocity be v_d.
Time taken to cover length l is –

t = \(\frac{l}{v_{d}}\)
l = \(\frac { Q }{t }\)
= \(\frac { nAel }{t }\)
l = nAev_d,
( v_d = \(\frac { distance}{time }\) = \(\frac { l }{t }\)
This is the required relationship.

Question 27.
Write four differences between electromotive force and potential difference.
Or
Define e.m.f. of a cell and potential difference. Give differences between them.
Answer:
e.m.f.: Work done in flowing 1 coulomb charge through a circuit is called e.m.f. of a cell When the terminals are not connected to an external circuit, the maximum potential difference between the terminals is equal to the e.m.f. of the cell. Unit of e.m.f is volt.

Potential difference:
The difference of potentials of any two points of the circuit is called potential difference.
Or
Work done in bringing unit positive charge from one point to another is called potential difference between these two points.

Differences between e.m.f. and potential difference:
e.m.f.:

• The maximum potential difference bet-ween the terminals of a cell is called its e.m.f., when the cell is in open circuit.
• This term is used for the electric sources as generator, cell, battery, dynamo, etc.
• It is established even the circuit is off.
• e.m.f. does not depend upon the resistance of the circuit.

Potential difference:

• Difference of potential of any two points of the circuit is called potential difference.
• This term is used for any two points of the circuit.
• It is established till the current is flowing through the circuit.
• It depends upon the resistance of the circuit

Question 28.
What do you understand by internal resistance of a cell ? On what factors does It depend and how ?
Or
What do you mean by internal resistance of a cell ? Write the factors affecting it.
Answer:
The resistance offered by the electrolyte of the cell during the flow of current inside the cell is called its internal resistance.
The following factors affect the internal resistance:

• Distance between the electrodes:
  As the distance increases, the internal resistance increases.
• Area of the immersed electrodes:
  As the area increases, the internal resistance decreases.
• Concentration of the electrolyte:
  As the concentration is more, the internal resistance is more.
• Temperature:
  The increase of temperature, decreases the internal resistance.

Question 29.
Establish the relationship between internal resistance of a cell, e.m.f. and extecoafresistance.
Or
Establish the relationship between the electromotive force, potential difference and internal resistance of a cell.
Answer:

Let e.m.f. of a cell be E and its internal resistance is r. If current / is flowing through a resistance R, then by Ohm’s law,
l = \(\frac { V}{R }\) ……………(1)
Where, V is the potential difference across the resistance. Now, total e.m.f. of the circuit = E and total resistance of the circuit = R + r
l = \(\frac {E}{R+r }\)
By eqns. (1) and (2), we get
\(\frac {V}{R}\) = \(\frac {E}{R+r }\)
VR + Vr = ER
Vr = ER – VR
r = \(\frac {R(E – V)}{V}\)
r = R(\(\frac {E}{V}\) – 1)
This is the required relationship.

Question 30.
Explain Kirchhoff’s laws of distribution of current through the different conduct^£
Or
Write down the Kirchhoff’s laws relating to the distribution of electric current.
Or
State and explain Kirchhoff’s laws.
Answer:
Kirchhoff’s laws:
(i) The algebraic sum of current meeting at any junction in a circuit is zero. In this law, the currents flowing towards the junction are considered as positive and those flowing  way from the junction as negative. As shown in the figure, we have

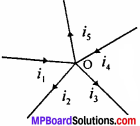
i₁ – i₂ – i₃ – i₄ – i₅ = 0
i₁ + i₄ = i₂ + i₃ + i₅

(ii) in any closed mesh (or loop) of an electrical circuit, the algebraic sum of the product of the currents and resistances is equal to the total e.m.f. of the mesh. If we go along the direction of conventional current, the potential difference will be taken as negative and opposite to it will be positive. Inside the cell, if we move from low to high potential, along the direction of conventional current, the e.m.f. will be positive.

For loop 1,
E₂ – i₂R₂ – (i₁ + i₂ )R₃ = 0
or E₂ = i₂R₂ + (i₁ + i₂ )R<sub>3

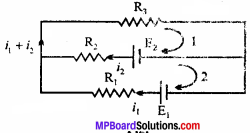
For loop 2,
i2R2 – E2 – i1R1 + E1 = 0
or E1 – E2 = i1R1 – i2R2</sub>

Question 31.
Derive the principle of Wheatstone bridge by Kirchhoffs law.
Or
Explain the principle of Wheatstone bridge and obtain the expression for balance condition by Kirchhoff s laws.
Answer:
Principle of Wheatstone bridge:
Four resistances P, Q, R and S are connected to form a quadrilateral ABCD. A cell E is connected across the diagonal AC and a galvanometer across BD. When the current is flown through the circuit and galvanometer does not give any deflection, then the bridge is said to be balanced. In this condition,
\(\frac { p }{ Q }\) = \(\frac { R }{ S }\)
This is the principle of Wheatstone bridge.

Formula derivation:
Let the current i is divided into two parts and i2, flowing through P, Q and R, S respectively. In the position of equilibrium, the galvanometer shows zero deflection, i.e,, the potential of B and D will be equal. In the closed mesh ABDA, by Kirchhoffs second law, we get

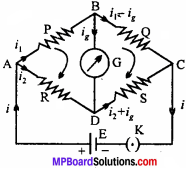
i₁P – i₂R = 0
or i₁ P = i₂R ……….(1)
Similarly, in the closed mesh BCDB, we have
i₁Q – i₂S = 0
or i₁Q = i₂S ……….(2)
Dividing eqn. (1) by eqn. (2), we get
\(\frac{i_{1} P}{i_{1} Q}=\frac{i_{2} R}{i_{2} S}\)
\(\frac{P}{Q}\) = \(\frac{R}{S}\)
This is Wheatstone bridge principle or principle of balance.

Question 32.
Explain the principle of potentiometer.
Answer:
Let AB be the wire of potentiometer of length L. A storage cell C, a key K and a rheostat Rh are connected in series with the resistance wire.
When the key is inserted, the current starts flowing through the circuit and a potential difference is established between A and B, let it is V.
∴ Potential gradient, P = \(\frac{V}{L}\)

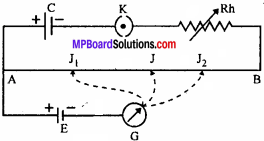
Now, the +ve terminal of the experimental cell is connected to A and -ve to galvanometer which is connected to jockey J. When jockey is touched near A, we get the deflection in one side and if it is touched near B, the deflection is in other side. Thus, a point on AB is found such that galvanometer gives no deflection. Hence, no current flows through the galvanometer and get the null point J.

In this balanced position,
e.m.f. of the cell = Potential difference between A and J
If the length of AJ = l.
∴ E = pl
Thus, knowing p and E can be calculated.
This is the principle of potentiometer.

Question 33.
On what factors the resistance of a wire or conductor depends ? Define specific resistance and write its unit.
Or
On what factors the resistance of a conductor depends and how ?
Answer:
The factors affecting the resistance are:

• Length: The resistance of conductor is directly proportional to the length of the conductor i.e., R ∝ l
• Area of cross – section: The resistance of a conductor is inversely proportional to the area of cross – section of the conductor i.e., R ∝ \(\frac{l}{A}\)
• Temperature: Increase in temperature, increases the resistance.

Combining above two laws, we get,
R ∝ \(\frac{l}{A}\)
R = p \(\frac{l}{A}\)
Where, p= a constant, called specific resistance of the material of the conductor.
Specific resistance:
We have,
R = p \(\frac{l}{A}\)
Let l = 1 And A = l, then
R = P

Thus, the specific resistance of a material is defined by the resistance of unit length and unit area of cross-section of that material.
Unit: Now, p = \(\frac{R.A}{l}\)
= \(\frac{Unit of R x Unit of A}{Unit of l}\)
= \(\frac{\mathrm{ohm} \times \mathrm{m}^{2}}{\mathrm{m}}\) = Ohm x m = Ω x m

Question 34.
What do you understand by specific resistance or resistivity of a conductor ? Give its unit and dimensional formula.
Answer:
For specific resistance of a conductor: Refer Short Answer: Type Q. No. 33(iii). Dimensional formula of specific resistance is determined as:
As p = \(\frac{RA}{l}\)
[p] = \(\frac{[R][A]}{[l]}\)
[R] = \(\frac{[V]}{[l]}\) = \(\frac{W/P}{[l]}\) = \(\frac{\left[\mathrm{ML}^{2} \mathrm{T}^{-2}\right] /[\mathrm{AT}]}{[\mathrm{A}]}\)
= \(\frac{\left[\mathrm{ML}^{2} \mathrm{T}^{-3} \mathrm{A}^{-1}\right]}{[\mathrm{A}]}\) = [ML²T^-3A^-2
[p] = \(\frac{\left[\mathrm{ML}^{2} \mathrm{T}^{-3} \mathrm{A}^{-2}\right]\left[\mathrm{L}^{2}\right]}{[\mathrm{L}]}\)
= \(\left[\mathrm{ML}^{3} \mathrm{T}^{-3} \mathrm{A}^{-2}\right]\)

Question 35.
Give differences between specific resistance and resistance.
Answer:
Differences between specific resistance (resistivity) and resistance:

Specific resistance:

• It is defined by the resistance offered by the conductor of unit length and unit area of cross – ection.
• Its unit is ohm x m.
• It does not depend upon the length and area of cross – ection.

Resistance:

• The hindrance offered by a conductor to the flow of current is called electrical resistance.
• Its unit is ohm.
• It depends upon the length and area of cross-section of the conductor.

Question 36.
Evaluate It and I₂ as shown in the figure.

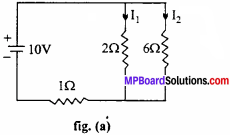
Solution:
Equivalent figure of fig. (a) is fig. (b)
In closed current BEFC, by Kirchhoff s second law,
2l₁ – 6I₂ = 0
or I₁ = 3I₂ …….(1)
In closed path ABCD
2I₁ + l(l₁ + l₂) = 10
3I₁ + I₂ = 10 …….(2)

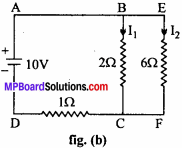
From eqns. (1) and (2),
3 x 3I₂ + I₂ = 10
or 9I₂ + I₂ = 10
or I₂ = 1 amp.
Putting the value of 12 in eqn. (1) we get,
I₁ = 3 x l = 3 amp

Question 37.
Three resistors R₁ R₂ and R₃ are connected in series. Obtain the expression for the equivalent resistance.
Answer:
The series combination of three resistors having resistances R₁ R₂ and R₃ are shown in figure.

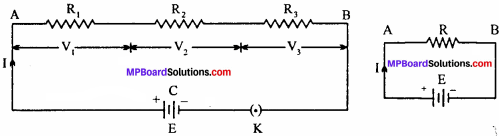
When this combination is connected to a cell (C) of e.m.f. E volt, then I current flows through combination.
Let the potential difference across R₁ R₂ and R₃ be V₁, V₂ and V₃ respectively. Then, by Ohm’s law,
V₁= IR₁ V₂ = IR₂ and V₃ = IR₃ .
If potential difference across A and B be V, then
V = V₁ + V₂ + V₃
or V = IR₁ + IR₂ + IR₃
V = I(R₁ + R₂ + R₃) ……(1)
If equivalent resistance of this combination be R, then
V = IR …..(2)
From eqns. (1) and (2), we get
1R = I(R₁ + R₂ + R₃)
or R = R₁ + R₂ + R₃ …(3)
Thus, when a number of resistances are connected in series with each other, the equivalent resistance of the combination is equal to the sum of their individual resistances.

Question 38.
Find out equivalent resistance of the three resistances R₁ ,R₂ and R₃ connected in parallel combination.
Answer:
The resistances R₁ ,R₂ and R₃ are connected in parallel as shown in adjacent figure. As all the resistances are connected between two points A and B, hence the potential difference between two points will be same for all. Let it be V. Let I be the total current. This current is divided into three parts at point A. If through R₁, R₂ and R₃; currents I₁ I₂ and I₃ are respectively flowing. Then,

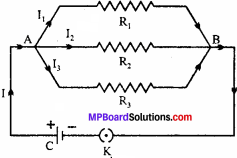
I = I₁ + I₂ + I₃
By Ohm’s law,
I₁ = \(\frac{V}{R_{1}}\), I₂ = \(\frac{V}{R_{2}}\), I₃ = \(\frac{V}{R_{3}}\)
I = \(\frac{V}{R_{1}}\) + \(\frac{V}{R_{2}}\) + \(\frac{V}{R_{3}}\) ……….(1)
If the equivalent resistance of this combination be R, then
I = \(\frac{V}{R}\) ……….(2)
From eqns. (1) and (2), we have
\(\frac{V}{R}\) = \(\frac{V}{R_{1}}\) + \(\frac{V}{R_{2}}\) + \(\frac{V}{R_{3}}\)
\(\frac{1}{R}\) = \(\frac{1}{R_{1}}\) + \(\frac{1}{R_{2}}\) + \(\frac{1}{R_{3}}\) …………(3)
Thus, if a number of resistances are connected in parallel, the reciprocal of equivalent resistance of the combination is equal to the sum of the reciprocals of their individual resistances.

Current Electricity Long Answer Type Questions

Question 1.
Describe an experiment to compare the e.m.f. of two cells by potentiometer onTne following points :

1. Circuit diagram
2. Derivation of formula
3. Two precautions.

Or
Describe an experiment to compare the e.m.f. of two cells using a potentiometer under the following heads :

1. Labelled diagram of electric circuit
2. Formula used
3. Observation table
4. Two main precautions.

Answer:
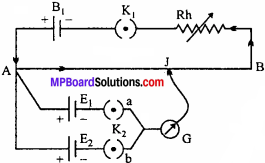
1. Circuit diagram:
AB → Potentiometer wire
B₁ → Lead accumulator
K₁ → Plug key
Rh → Rheostat
E₁ E₂ → Experimental cells
K₂ → Two ways key
G → Galvanometer
J → Jockey.

2. Derivation of formula:
Let the first cell is having e.m.f. E, and the balancing point is obtained at distance l₁. Then by the principle of potentiometer,
E₁ = pl₁ ……(1)
Where, p is potential gradient.
Let E₂ is the e.m.f. of second cell whose balancing point is at l₂, then
E₂ = pl₂ ……(2)
Dividing eqn. (1) by eqn. (2), we get,
\(\frac{E_{1}}{E_{2}}=\frac{pl_{1}}{pl_{2}}=\frac{l_{1}}{l_{2}}\)

3. Observation tab:

4. Precautions:
The e.m.f. of lead accumulator should be greater than that of experimental cells. All the positive terminals should be connected to one point

Question 2.
Determine the internal resistance of a cell by potentiometer on the following points:

1. Labelled circuit diagram
2. Derivation of formula
3. Precautions.

Or
Determine an experiment to find out the internal resistance of a cell by potentiometer under the following points :

1. Labelled circuit diagram
2. Formula derivation
3. Observation table
4. Precautions (any two).

Answer:
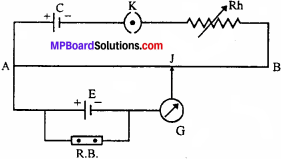
1. Circuit diagram:
AB → Potentiometer wire
C → Storage cell
K → Plug key
Rh → Rheostat
E → Experimental cell
R.B. → Resistance box
G → Galvanometer
J → Jockey.

2. Formula derivation:
Let the e.m.f. of the cell is E and its internal resistance is r. When it is connected to external resistance R, its potential difference is V, then

r = R (\(\frac{E}{V}\) – 1) ……..(1)
When R is not connected, then let the balance point is found at a distance l₁ from A.
∴ E = pl₁
Similarly, when R is also connected, then let the balanced point is obtained at a distance l₂ from A.
∴ V = pl₂
Now, putting these values in eqn. (1), we get
r = R \(\left(\frac{\rho l_{1}}{\rho l_{2}}-1\right)\) = R \(\left(\frac{l_{1}}{l_{2}}-1\right)\)
This is the required formula

3. Observation table :

4. Precautions:

• The e.m.f. of the storage cell (C) must be greater than that of experimental cell (£).
• All the positive terminals must be connected to a single point

Question 3.
How are the cells connected in mixed combination ? Derive an expression for current flowing through external resistance.
Or
Prove that the current in the external circuit for a mixed combination of cells is maximum, when the internal resistance of the combination equals the external resistance.
Answer:
In this combination, series connections of equal number of cells are connected in parallel and finally providing one +ve and one -ve terminal as shown in Fig. (a). These two terminals are connected to the ends of an external resistance R so that current starts flowing through the resistance.

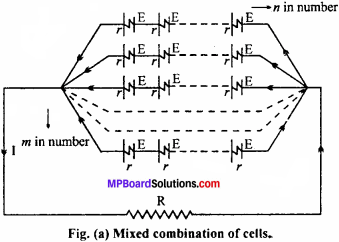
Suppose n cells are connected in series combination and let m be the number of such series connected in parallel. Let the e.m.f. of each cell be E and internal resistance be r. Total e.m.f. of each series combination i.e, for a row, will be nE and total internal resistance will be nr. Hence, the equivalent becomes as given in Fig. (b).

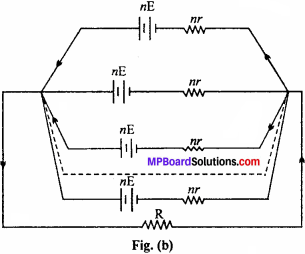
As all the cells are now in parallel, so total e.m.f. of the combination will also be nE and total internal resistance will be r’. This is shown in Fig. (c). As each resistor is of value nr and nr such resistors are connected in parallel, hence total internal resistance r’ will be calculated as:

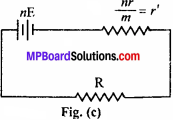
\(\frac{1}{r’}\) = \(\frac{1}{nr}\) + \(\frac{1}{nr}\) + ………. + m terms = \(\frac{m}{nr}\) or r’ = \(\frac{nr}{m}\)
As R is the external resistance, then r’ and R are in series. Hence, total resistance of combination becomes,
R_total = R + r’ = R + \(\frac{nr}{m}\)
The current through the circuit will be given by Ohm’s law as

l = \(\frac{Total e.m.f.of battery }{Total resistance of circuit}\)

l = \(\frac{n \mathrm{E}}{\mathrm{R}+\frac{n r}{m}}\) = \(\frac{m n \mathrm{E}}{m \mathrm{R}+n r}\) ……….(1)

This is the expression for the current. For the current to be maximum, mR+nr must be minimum

mR + nr = \((\sqrt{m \mathrm{R}})^{2}+(\sqrt{n r})^{2}-2 \sqrt{m \mathrm{R}} \sqrt{n r}+2 \sqrt{m \mathrm{R}} \sqrt{n r}\) (as subtracting and adding \(2 \sqrt{m \mathrm{R}} \sqrt{n r}\))

= \((\sqrt{m \mathrm{R}}-\sqrt{n r})^{2}+2 \sqrt{m \mathrm{R}} \times \sqrt{n r}\)

But \((\sqrt{m \mathrm{R}}-\sqrt{n r})^{2}\) cannot be negative, as it is a perfect square.

mR + nr will be minimum, only when \((\sqrt{m \mathrm{R}}-\sqrt{n r})^{2}\) = 0

or \(\sqrt{m \mathrm{R}}-\sqrt{n r}\) = 0

\(\sqrt{m \mathrm{R}}\) = \(\sqrt{n r}\) ⇒ mr = nr ………(2)
∴ R = \(\frac{n r}{m}\) ………..(3)

Hence, the external resistance should be equal to the internal resistance of the battery. Under this condition the current supplied by the battery to the resistance R is maximum. The value of maximum current can be obtained by putting eqn. (2) in eqn. (1).

∴ I_max = \(\frac{mnE}{mR + mR}\)

= \(\frac{mnE}{2mR}\) = \(\frac{nE}{2R}\)
On substituting mR = nr, we get

I_max = \(\frac{mnE}{nr + nr}\) = \(\frac{mnE}{2nr}\)

= \(\frac{mE}{2r}\) .

Question 4.
explain the experiment of determining the unknown resistance of a wire with he help of meter bridge on the following points:

1. Electrical circuit
2. Principle.

Or
Describe an experiment to determine the unknown resistance by meter bridge on following points :

1. Circuit diagram
2. Description of apparatus
3. Observation table
4. Precautions.

Or
What are the possible errors in performing the experiment with metre bridge and how they can be removed ?
Answer:
1. Circuit diagram:

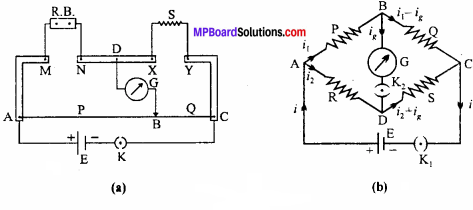
Where ,
AC→ wire
E → cell
R → resistance box
S → unknown resistance,
G → galvanometer
K → key.

2. Description of apparatus:
It consists of 1 meter long manganin or constant resistance wire, fixed on a wooden plank. Thick steel or brass strips are fixed as shown in the figure with two gaps. In one gap, resistance box R and in other, unknown resistance S are connected. A, C and D are terminals. A jockey slides on the wire.

3. Formula derivation or principle:
Meter bridge consists of 1 m long constant-an wire AC, fixed on a wooden plank. In two gaps resistance R and unknown resistance S are connected. Galvanometer G is connected between B and D, where B is sliding point i. e., jockey.
A cell E, with a plug key K is connected between A and C.
Let null point is obtained at a distance l from A.
∴ AB = l cm
and BC = (100 – l)cm
If x be the resistance per unit length, then Resistance offered by AB is P = lx
and resistance offered by BC is Q = (100 – l)x
Now, by the principle of Wheatstone bridge,

\(\frac{P}{Q}\) = \(\frac{R}{S}\)

\(\frac{lx}{(100 – l)}\)

S = \(\frac{R(100 – l)}{l}\)
Wheatstone bridge is sensitive when all the four resistances are of same order. Hence, metre bridge is also suitable for the resistance of same order.

4. Observation table:

5. Precautions:

• The connection should be tight.
• The plugs of R.B. should not be loose.
• The current should be passed only when readings are to be taken.
• Jockey should not be rubbed with the wire.

Possible errors and their removal:
1. It might happen that the wire is not uniform. To remove this error, balance point should be obtained at the-middle.

2. During’the experiment, it is assumed that the resistance of L shaped plates are negligible, but actually it is not so. The error created due to this is called end error. To remove this error, the resistance box and the unknown resistance must be interchanged and then the mean reading should be taken.

3. If the jockey is pressed for a long period of time, then it gets heated and its resistance changes. Hence, jockey must not be pressed for a long interval.

Question 5.
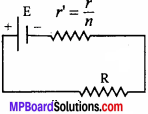
How are cells connected in series ? Derive an expression for current flowing through outer circuit. When is this combination useful ?
Answer:
In this combination, the -ve terminal of one cell is connected to the + ve terminal of second cell, whose -ve terminal is connected to the +ve terminal of third one and so on as shown in Fig. (a). Let n cells each of e.m.f. E and internal resistance r be connected in series through an external resistance R, then

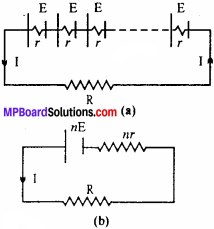
Total e.m.f. of this combination = n E ’ and total internal resistance
r’ = r + r + r +…………….+ n times
= nr
The series combination of n cells is equivalent to a single cell having e.m.f. «E and internal resistance nr. This is shown in Fig. (b).
Now nr and external resistance R are in series. So, the equivalent resistance of circuit becomes R + nr Applying Ohm’s law, current flowing through the circuit is given by –
l = \(\frac{e.m.f. of battery }{Total resistance}\)
= \(\frac{nE }{nr + R}\)
This is the expression for current flowing through the external resistance R. If r « R, then nr + R * R.
Hence, from eqn. (1), we get
l = n. \(\frac{E }{R}\)
= n x Current flowing through each cell.

Utility:
Thus, if the internal resistance of each cell is negligible as compared to external resistance, the current flowing through the battery is n times the current supplied by each cell.
So, the cells should be connected in series only when the internal resistance of each cell is much less than the external resistance.

Question 6.
n cells are connected in parallel combination with internal resistance. Derive an expression for current flowing through external resistance. When is this combination useful?
Answer:
Let n cells be connected in parallel and e.m.f. of each cell be E and internal resistance be r. Since, all the positive terminals of cells connected to point A and -ve terminals connected to the point B, the total e.m.f. of battery will be E (because in parallel combination potential difference remains same).

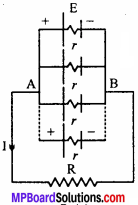
Since the cells are connected in parallel, therefore their internal resistance will also be in parallel combination. Let the equivalent internal resistance be r’
∴ \(\frac{1 }{r’}\) = \(\frac{E }{R}\) + \(\frac{E }{R}\) + …………. + n times \(\frac{n }{r}\)
or r’ = \(\frac{r }{n}\)
Hence, the equivalent circuit becomes

Where, r’ is the total resistance of the combination of cells. As R and r’ are in series, so the total resistance of the circuit becomes
= R + r’ = R + \(\frac{r }{n}\)
Current through external resistance R will be given by Ohm’s law as
l = \(\frac{Total e.m.f.of battery }{Total resistance of circuit}\)
l = \(\frac{E}{R+\frac{r}{n}}\) = \(\frac{n E}{n R+r}\)
This is the required expression.
If R << r, then nR + r≈r
Now, from eqn. (1), we have
I = n \(\frac{E}{r}\) = n x Current given by one cell .

Utility:
Thus, if internal resistance of each cell is much greater than the external resistance, then the current flowing through the battery is n times the current through each cell i.e., maximum current is obtained. So, the cells should be connected in parallel when internal resistance of each cell is much greater than the external resistance.

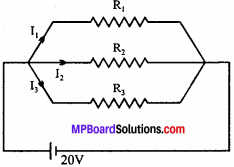
Current Electricity Numerical Questions

Question 1.
The storage battery of a car has an emf of 12 V. If the internal resistance of the battery is 0.4Ω, what is the maximum current that can be drawn from the battery? (NCERT)
Solution:
Given: E = 12 V; r – 0.4 Ω
Current l = \(\frac{E}{R+r}\)
For current to be maximum R = 0
I_max = \(\frac{E}{r}\) = \(\frac{12}{0.4}\) = 30A

Question 2.
A battery of emf 10V and internal resistance 3) is connected to a resistor. If the current in the circuit ¡s 0.5A. What is the resistance of the resistor? What is the terminal voltage of the battery when the circuit is closed? (NCERT)
Solution:
Given:
E =10V; r = 3Ω l = 0.5A

l = \(\frac{E}{R + r}\)
R+r = \(\frac{E}{l}\)
R = \(\frac{E}{l}\) – r = \(\frac{10}{0.5}\) – 3 = 20 – 3 = 17Ω
Now, V = E – lr = 10 – 0.5 x 3 = 10 – 1.5 = 8.5V

Question 3.
(a) Three resistance IΩ, 2Ω and 3Ω are combined in series. What is the total resistance of the combination ?
(b) If the combination is connected to a battery of emf 12V and negligible internal resistance, obtain the potential drop across each resistor. (NCERT)
Solution:
(a) Given:
R₁ = IΩ; R₂ = 2Ω; R₃ = 3Ω
R₂ = R₂ + R₂ + R₂ = 1 + 2 + 3 = 6Ω .
(b) E = 12V; r = 0
l = \(\frac{E}{R+r}\) = \(\frac{E}{R_{S}+0} = \frac{12}{6}\)
I = 2A
Potential difference across (R₁)
V₁ = IR₁ = 2 x l = 2V
Potential difference across (R₂)
V₂ = IR₂ = 2 x 2 = 4V
Potential difference across (R₃)
V₃ = IR₃ = 2 X 3 = 6V.

Question 4.
(a)Three resistors 2Ω, 4Ω and 5Ω are combined in parallel. What is the total resistance of the combination ?
(b) If the combination is connected to a battery of emf 20V and negligible internal resistance, determine the current through each resistor and the total current drawn from the battery. (NCERT)
Solution?:
(a) Given:
R₁ = 20; R₂ = 40; R₃ = 50
Equivalent resistance:
\(\frac{1}{R_{p}}\) = \(\frac{1}{R_{1}}\) + \(\frac{1}{R_{2}}\) + \(\frac{1}{R_{3}}\)
= \(\frac{1}{2}\) + \(\frac{1}{4}\) + \(\frac{1}{5}\) = \(\frac{10+5+4}{20}\) = \(\frac{19}{20}\)
∴ \(\frac{1}{R_{p}}\) = \(\frac{20}{19}\) Ω

(b) E = 20V; r = 0
Current through different resistors,
l₁ = \(\frac{E}{R_{1}}\) = \(\frac{20}{2}\) = 10A
l₂ = \(\frac{E}{R_{2}}\) = \(\frac{20}{4}\) = 5A
l₃ = \(\frac{E}{R_{3}}\) = \(\frac{20}{5}\) = 4A
Total current drawn
l = l₁ + l₂ + l₃ = 10 + 5 + 4 = 19A

Question 5.
At room temperature (27°C) the resistance of a heating element is 100Ω. What is the temperature of the element if the resistance is found to be 117 Ω, given that temperature coefficient of the resistor material is 1.70 x 10^-4 °C^-1 ? (NCERT)
Solution:
Given:
t₁ = 27 °C
R₁ = 1000
R₂ = 1170
α = 1.70 x 10^-4 °C^-1
We know that, α = \(\frac{R_{2}-R_{1}}{R_{1}\left(t_{2}-t_{1}\right)}\)
t₂ – t₁ = \(\frac{R_{2}-R_{1}}{R_{1} \alpha}\)
= \(\frac{117-100}{170 \times 10^{-4} \times 100}\)
t₂ – t₁ = 1000
t₂ = 1000 + t₁ = 1000 + 27 = 1027 °C

Question 6.
A negligible small current is passing through a wire of length 15 m and uniform cross – section 6.0 x 10^-7 m² and its resistance is measured to be 5.0ΩWhat is the resistivity of the material at the temperature of the experiment ? (NCERT)
Sol. Given:
l = 15m; A = 6.0 x l0^-7m²; R = 5.0Ω
using R = \(\frac { pl }{ A }\)
p = \(\frac {RA}{ l }\) = \(\frac{5 \times 6 \times 10^{-7}}{15}\) = 2.0 x l0^-7Ωm

Question 7.
Determine the current in each branch of the network shown in figure. (NCERT)

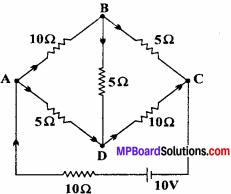
solution:
\(\frac {P}{ Q }\) = \(\frac {10}{5}\) = \(\frac {2}{ 1 }\) and \(\frac {R}{S }\) = \(\frac {5}{ 10 }\) = \(\frac {1}{ 2 }\).
i.e \(\frac {P}{ Q}\) = \(\frac {R}{ S}\)

Therefore, bridge is not in equilibrium. Current flowing through different branches is as shown in fig. Now applying Kirchhoffs loop rule.

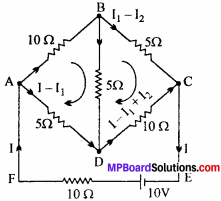
For loop ABDA
10I₁ + 5I₂ – 5(I – I₁) = 0
3I₁ + l₂ – I = 0 ……(1)

For loop BCDB.
5(I₁ – I₂) – 10 (I – l₁ + I₂) – 5I₂ = 0
or I₁ – I₂ – 2 (I – I₁ + I₂) I₁ = O
or 3I₂ – 4I₂ – 2I = 0 …..(2)
By eqns. (1) and (2), 5I₂ + I = 0
I = – 5I₂
I₂ = – \(\frac {1}{ 5 }\) I …….(3)
And I₁ = \(\frac {2}{ 5 }\) I …….(4)

For loop ADCA,
5(I – I₁) + 10 (1 – l₁ + l₂) + 10I = 10
5I – 3I + 2I₁ = 2

Question 8.
Find out effective resistance between points A and B for circuit given below:

Solution:
\(\frac {1}{ R}\) = \(\frac {1}{ 2 + 2 + 2 }\) + \(\frac {1}{ 3 }\)

\(\frac {1}{ R}\) = \(\frac {1}{6}\) + \(\frac {1}{3}\)

\(\frac {1}{ R }\) = \(\frac {1 + 2}{ 6 }\) = \(\frac {3}{6}\)
R = \(\frac {6}{3}\) = 2Ω

Question 9.
Find out effective resistance between points A and B for circuit given below:

\(\frac{1}{\mathrm{R}_{1}}\) = \(\frac {1}{ 4}\) + \(\frac {1}{ 4}\) = \(\frac{1}{\mathrm{R}_{1}}\) = \(\frac {2}{ 4}\)

R₁ = \(\frac {4}{2}\) = 2Ω

\(\frac{1}{\mathrm{R}_{2}}\) = \(\frac {1}{ 6}\) + \(\frac {1}{ 6}\) =\(\frac{1}{\mathrm{R}_{2}}\) = \(\frac {2}{ 6}\)

R₂ = \(\frac {6}{ 2}\) = 3Ω
Effective resistance R = R₁ + R₂
R = 2 + 3 = 5Ω

Question 10.
10⁹ electrons flows from point A to B in 10^-3 second. Find out magnitude and direction of electric current.
Solution:
Formula: I = \(\frac {ne}{t}\)
Given: n = 10⁹ t = 10^-3 sec.
Putting the given value in the formula, we get
I = \( \frac{10^{9} \times 16 \times 10^{-19}}{10^{-3}}\)
or l = 1.6 x l 0^-7 ampere.
Direction of electric current will be from B to A. Ans.

Question 11.
150 m A current flows through a conductor. How many electrons will flow through it in 20 sec ?
Solution:
Given:
I = 150 mA = 0.15 A, t = 20 sec.
Formula:
n = \(\frac {It}{e}\) = \(\frac{0.15 \times 20}{1 \cdot 6 \times 10^{-19}\)

n = \(\frac{3}{1 \cdot 6} \times 10^{19}\) = 1.875 x 10¹⁹

Question 12.
200 mA current flows through a conductor. How many electrons will flow through it in 5 sec ?
Solution:
Given:
I = 200 mA = 0.2 A, t = 5 sec
Formula:
n = \(\frac {It}{e}\) = \(\frac{0\cdot 2\times 5}{1\cdot 6\times 10^{-19}}\)

n = \(\frac{1}{1 \cdot 6} \times 10^{19}\)
n = 0.625 x 10¹⁹

Question 13.
The length of a wire becomes twice when stretched. How many times resistance will increase ?
Solution:
On stretching the wire, radius of the wire will decrease but volume will remain same. Let l₁ and r₁ be initial length and radius of wire respectively. On stretching, the length becomes l₂ say and radius r₂
Initial volume = Final volume

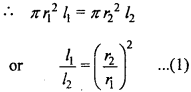
From the formula, R = p \(\frac {1}{A}\)

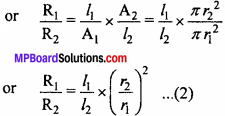
Putting the value of \(\left(\frac{r_{2}}{r_{1}}\right)^{2}\) from eqn. (1) in eqn. (2), we get

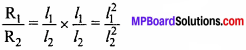
As per the question, l₂ = 2l₁
\(\frac{R_{1}}{R_{2}}\) = \(\left(\frac{l_{1}}{2 l_{1}}\right)^{2}\) = \(\frac {1}{4}\)
R₂ = 4R₁
Hence, the resistance of wire is increased four times.

Question 14.
The ratio of area of cross-section of two wires made of same metal and equal length is 2 : 1. It applied potential difference between their ends are same then what will be the ratio of current among them ?
Solution:

Question 15.
The ratio of length of two wire, made of same metal and equal area of cross-section is 2 : 1. If the applied potential difference between their ends are same, then what will be the ratio of current following among them ?
Solution:

Question 16.
125 mA current flows through a lamp in 10 sec. How many electrons will flow across it ?
Solution:
Given:
I = 125 mA = 0.125 A. t = 10 sec.

MP Board Class 12th Physics Important Questions