MP Board Class 12th Maths Book Solutions Chapter 9 अवकल समीकरण Ex 9.4

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 9 अवकल समीकरण Ex 9.4 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 9 अवकल समीकरण Ex 9.4

1 से 10 तक के प्रश्नों में, प्रत्येक अवकल समीकरण का व्यापक हल ज्ञात कीजिए।
प्रश्न 1.
\(\frac{d y}{d x}=\frac{1-\cos x}{1+\cos x}\)
हल:

प्रश्न 2.
\(\frac{d y}{d x} \sqrt{4-y^{2}}\) (-2 < y < 2)
हल:

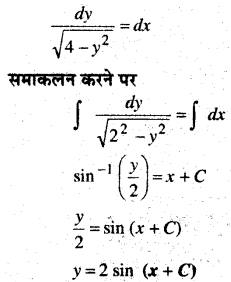
प्रश्न 3.
\(\frac{d y}{d x}\) + y = 1(y ≠ 1)
हल:
\(\frac{d y}{d x}\) = 1 – y
\(\frac{d y}{1-y}\) = dx
समाकलन करने पर

प्रश्न 4.
sec² x tan y dx + sec² y tan x dy = 0
हल:
sec² x tan y dx = – sec² y tan x dy

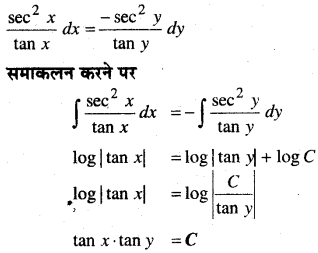
प्रश्न 5.
(e^x + e^-x)dy – (e^x – e^-x) dx = 0
हल:
(e^x + e^-x)dy = (e^x – e^-x) dx = 0

प्रश्न 6.
\(\frac{d y}{d x}\) = (1 + x²) (1 + y²)
हल:


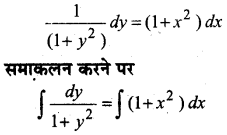
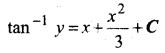
प्रश्न 7.
y log y dx – x dy = 0
हल:
दिया है :
y log y dx – x dy = 0
xy logy से भाग देने पर

प्रश्न 8.
x⁵\(\frac{d y}{d x}\) = -y⁵
हल:
x⁵\(\frac{d y}{d x}\) = -y⁵
⇒ y^-5 dy = -x^-5 dx
समाकलन करने पर

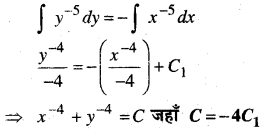
प्रश्न 9.
\(\frac{d y}{d x}\) = sin^-1x
हल:
\(\frac{d y}{d x}\) = sin^-1x
⇒ dy = sin^-1x dx
समाकलन करने पर


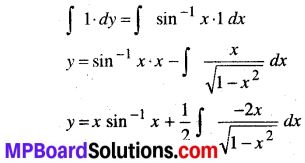
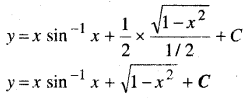
प्रश्न 10.
e^x tan y dx + (1 – e^x) sec²y dy = 0
हल:

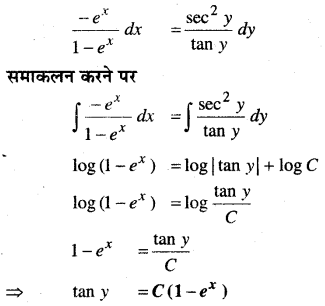
11 से 14 तक के प्रश्नों में, प्रत्येक अवकल समीकरण के लिए दिए हुए प्रतिबंध को संतुष्ट करने वाला विशिष्ट हल ज्ञात कीजिए।
प्रश्न 11.
(x³ + x² + x + 1)\(\frac{d y}{d x}\) = 2x² + x; y = 1 यदि x = 0.
हल:
(x³ + x² + x + 1)\(\frac{d y}{d x}\) = 2x² + x

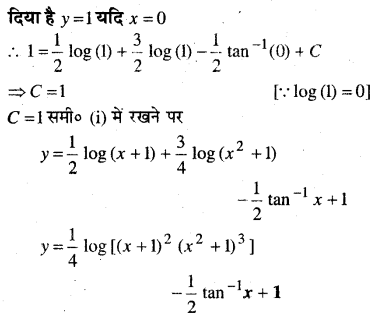
प्रश्न 12.
x (x² – 1)\(\frac{d y}{d x}\) = 1; y = 0 यदि x = 2
हल:
x (x² -1)\(\frac{d y}{d x}\) = 1

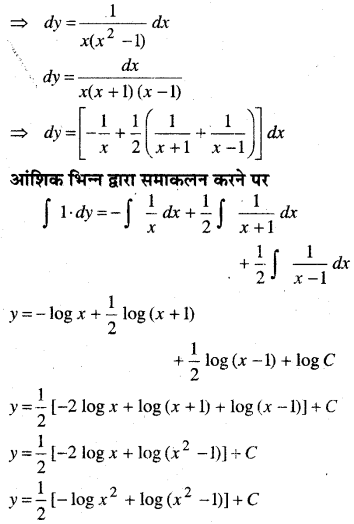
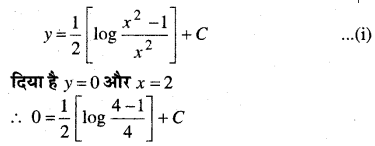
प्रश्न 13.
cos\(\left(\frac{d y}{d x}\right)\) = a (a ϵ R): y = 1 यदि x = 0
हल:
\(\frac{d y}{d x}\) = cos^-1 a ⇒ dy = (cos^-1a) dx
समाकलन करने पर
\(\int d y=\int\left(\cos ^{-1} a\right) d x\)
y = x cos^-1 a + C
इस समी० में y = 1 यदि x = 0 रखने पर
1= 0 + C ⇒ C = 1
C का यह मान समी० (i) में रखने पर
y = x cos^-1 a + 1
\(\frac{y-1}{x}\) = cos^-1a
⇒ cos\(\left(\frac{y-1}{x}\right)\) = a

प्रश्न 14.
\(\frac{d y}{d x}\) = y tan x; y = 1 यदि x = 0
हल:
⇒ \(\frac{d y}{y}\) = tan x dx
समाकलन करने पर
\(\int \frac{1}{y} d y=\int \tan x d x\)
logy = log sec x + log C
log y = log (C sec x)
y = C sec x …(i)
दिया है y = 1 यदि x = 0 तब समी० (i) से
1 = C sec 0 ⇒ C = 1
C = 1 समी० (i) में रखने पर ..
⇒ y = secx

प्रश्न 15.
बिन्दु (0, 0) से गुजरने वाले एक ऐसे वक्र का समीकरण ज्ञात कीजिए जिसका अवकल समीकरण y’ = e^x sinx है।
हल:
दिया है y’ = e^x sin x
या \(\frac{d y}{d x}\) = e^x sin x
⇒ dy = e^x sin x dx
समाकलन करने पर

प्रश्न 16.
अवकल समी० xy\(\frac{d y}{d x}\) = (x + 2)(y + 2) के लिए बिन्दु (1, – 1) से गुजरने वाला वक्र ज्ञात कीजिए।
हल:
दिया है xy\(\frac{d y}{d x}\) = (x + 2)(y + 2)

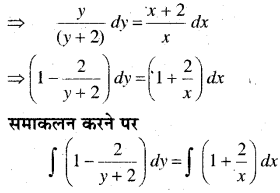
y – 2 log (y + 2) = x + 2 log x + C …(i)
∵ वक्र बिन्दु (1, -1) से गुजरता है अतः x = 1, y = -1
∴ -1 – 2 log (1) = 1 + 2 log (1) + C [∵ log 1 = 0]
-1 = 1 + C ⇒ C = -2
C = – 2 समी० (i) में रखने पर
y – 2 log (y + 2) = x + 2 log x + 2
⇒ y – x + 2 = 2 log x + 2 log (y + 2)
⇒ y – x’ + 2 = 2 [log x (y + 2)]
y – x + 2 = log [x² (y + 2)²]

प्रश्न 17.
बिन्दु (0, -2) से गुजरने वाले एक ऐसे वक्र का समीकरण ज्ञात कीजिए जिसके किसी बिन्दु (x, y) पर स्पर्श रेखा की प्रवणता और उस बिन्दु के ए निर्देशांक का गुणनफल उस बिन्दु के x निर्देशांक के बराबर है।
हल:
प्रश्नानुसार, y\(\frac{d y}{d x}\) = x (जहाँ \(\frac{d y}{d x}\) स्पर्श रेखा की प्रवणता है।)
y dy = x dx
समाकलन करने पर

प्रश्न 18.
एक वक्र के किसी बिन्दु (x, y) पर स्पर्श रेखा की प्रवणता, स्पर्श बिन्दु को, बिन्दु (-4, -3) से मिलाने वाले रेखाखण्डकी प्रवणता की दुगनी है। यदि यह वक्र बिन्दु (-2, 1)से गुजरता हो तो इस वक्र का समीकरण ज्ञात कीजिए।
हल:
दिया है बिन्दु (x, y) पर स्पर्श रेखा की प्रवणता = 2x [स्पर्श बिन्दु को (-4, -3) से मिलाने वाली रेखा की प्रवणता]

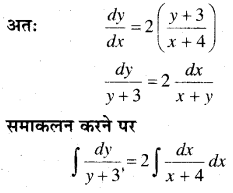
log (y + 3) = 2 log (x + 4) + log C
log (y + 3) = log (x + 4)² .C
⇒ y + 3 = (x + 4)².C …(i)
∵ वक्र बिन्दु (-2, -1) से गुजरता हैं इसलिए
x = -2, y = 1 रखने पर
4 = (2)² C = 4 = 4C
या C = 1
समी० (i) में C =1 रखने पर
– y + 3 = (x + 4)²

प्रश्न 19.
एक गोलाकार गुब्बारे का आयतन, जिसे हवा भरकर फुलाया जा रहा है, स्थिर गति से बदल रहा है। यदि आरम्भ में इस गुब्बारे की त्रिज्या 3 इकाई है और 3 सेकण्ड बाद 6 इकाई है, तो t सेकण्ड बाद उस गुब्बारे की त्रिज्या ज्ञात कीजिए।
हल:
माना किसी क्षण t गुब्बारे की त्रिज्या r तथा आयतन V है तब

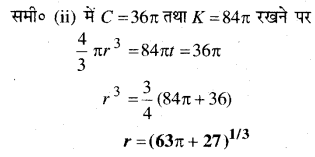
प्रश्न 20.
किसी बैंक में मूलधन की वृद्धि r% वार्षिक की दर से होती है। यदि 100 रु० 10 वर्षों में दुगने हो जाते हैं, तो का मान ज्ञात कीजिए। (log 2 = 0.6931)
हल:
माना किसी समय पर मूलधन P हैं तब प्रश्नानुसार,

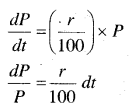
प्रश्न 21.
किसी बैंक में मूलधन की वृद्धि 5% वार्षिक की दर से होती है। इस बैंक में 1000 रु० जमा कराये जाते हैं। ज्ञात कीजिए कि 10 वर्ष बाद यह राशि कितनी हो जाएगी? (e^0.5 = 1.648)
हल:
किसी समय t पर मूलधन P हैं तब प्रश्नानुसार,

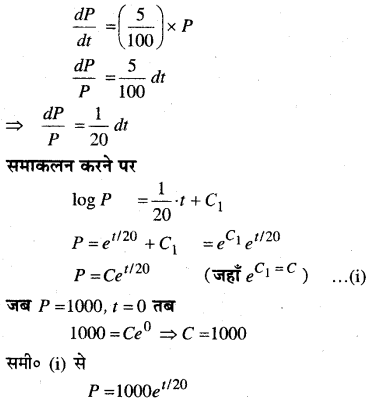
जब t = 10 वर्ष
P = 1000 e^10/20 ⇒ P = 1000e^0.5
P = 1000 × 1.648 (∵ e^0.5 = 1.648)
P = 1648 रु०
अत: 10 वर्ष बाद मूलधन 1648 रु० होगा।

प्रश्न 22.
किसी जीवाणु समूह में जीवाणुओं की संख्या 1,00,000 है। 2 घण्टों में इनकी संख्या में 10% की वृद्धि होती है। कितने घण्टों में जीवाणुओं की संख्या 2,00,000 हो जाएगी। यदि जीवाणुओं के वृद्धि की दर उनमें उपस्थित संख्या के समानुपाती है।
हल:
माना किसी समय t पर जीवाणुओं की संख्या y है।

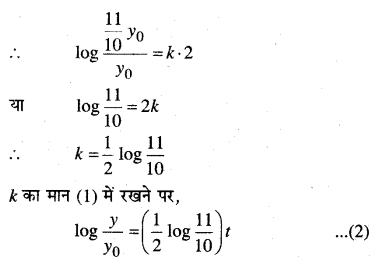
प्रश्न 23.
अवकल समीकरण \(\frac{d y}{d x}\) = e^x+y का व्यापक इल है
(A) e^x + e^-y = C
(B) e^x + e^y = C
(C) e^-x + e^y = C
(D) e^-x + e^-y = C
हल: