MP Board Class 12th Maths Book Solutions Chapter 8 समाकलनों के अनुप्रयोग Ex 8.1

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 8 समाकलनों के अनुप्रयोग Ex 8.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 8 समाकलनों के अनुप्रयोग Ex 8.1

प्रश्न 1.
वक्र y = x रेखाओं x = 1, x = 4 एवं x-अक्ष से घिरे क्षेत्र का प्रथम पाद में क्षेत्रफल ज्ञात कीजिए।
हल:
दिया है y² = x
या y = \( \sqrt{{x}} \)
वक्र का शीर्ष मूल बिन्दु है तब यह एक परवलय है।
∵ क्षेत्र POLM, x = 1, x = 4, x-अक्ष तथा वक्रों से घिरा है

प्रश्न 2.
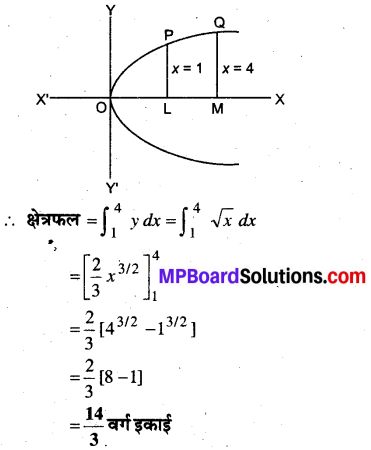
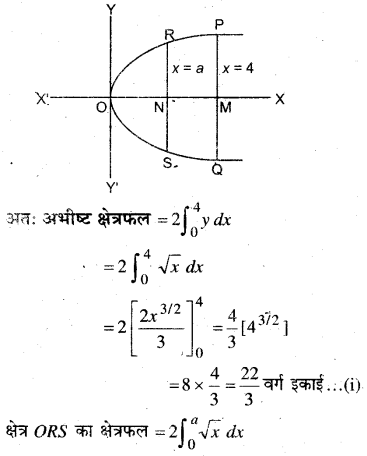
प्रथम चतुर्थांश में वक्र y² = 9x, x = 2, x = 4 एवं x-अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
वक्र y = 9x एक परवलय है जिसका शीर्ष (0, 0) है वक्र x-अक्ष के सममित है ।
क्षेत्र PORS, वक्र y² = 9x,
x = 2, x = 4 तथा x-अक्ष से घिरा है।
अब,
y² = 9x
y = 3\( \sqrt{{x}} \)

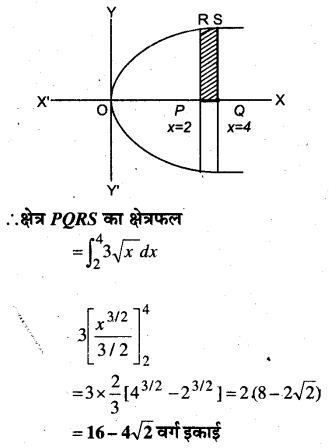
प्रश्न 3.
प्रथम चतुर्थांश में x² = 4y, y = 2, y = 4 एवं y-अंक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
दिया है x² = 4y एक परवलय है
जिनका शीर्ष मूल बिन्दु है।

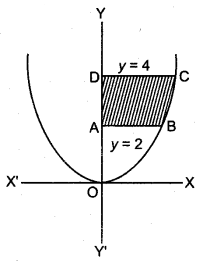
वक्र y = 2, y = 4 तथा v-अक्ष से घिरा है।
x² = 4y
या ⇒ x = 2\( \sqrt{{y}} \)
क्षेत्र ABCD का क्षेत्रफल

प्रश्न 4.
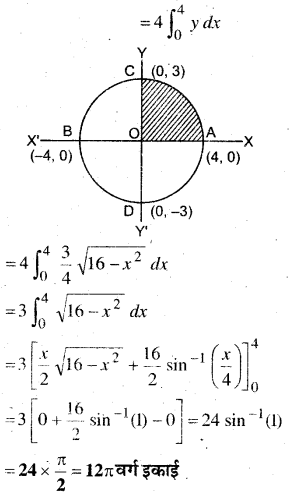
दीर्घवृत्त \(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\) से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
दीर्घवृत्त का समीकरण
\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\)
∵ समी० में x तथा ) की घात बराबर है अत: यह दोनों अक्षों के सममित हैं।
∴ दीर्घवृत्त का क्षेत्रफल = 4 × OACO का क्षेत्रफल

प्रश्न 5.
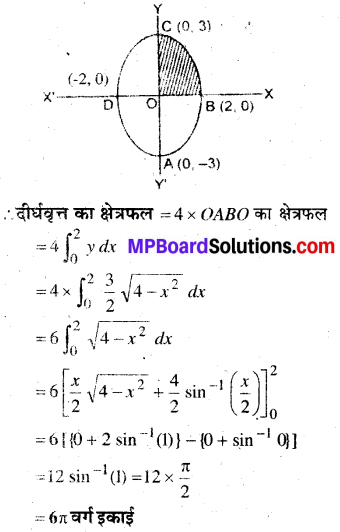
दीर्घवृत्त \(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\) से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
दीर्घवृत्त का समीकरण
\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\)
∵ समीकरण में x तथा y की घात बराबर है अतः दीर्घवृत्त दोनों अक्षों के सममित होगा।

प्रश्न 6.
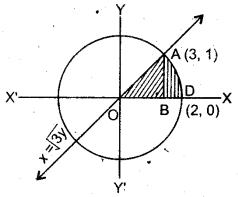
प्रथम चतुर्थांश में वृत्त x² + y² = 4 रेखा r = \( \sqrt{{3}} \)y एवं x-अक्ष द्वारा घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
वृत्त का समी० x² + y² = 4
वृत्त का केन्द्र (0, 0) तथा त्रिज्या 2 के समान हैं।

प्रश्न 7.
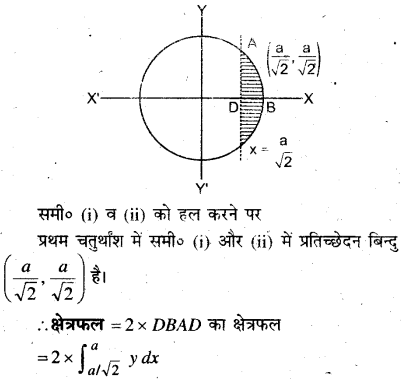
छेदक रेखा x = \(\frac{a}{\sqrt{2}}\) द्वारा वृत्त x² + y² = a² के छोटे भाग का क्षेत्रफल ज्ञात कीजिए।
हल:
वृत्त का समी० x² + y² = a² …(i)
\(\frac{a}{\sqrt{2}}\) …(ii)
समी० (i) से स्पष्ट है कि यह एक वृत्त है और समी० (ii) y-अक्ष के समान्तर \(\frac{a}{\sqrt{2}}\) मात्रक दूरी पर इसके दायीं ओर एक सरल रेखा है।

प्रश्न 8.
यदि वक्र x = y² एवं रेखा x = 4 से घिरा हुआ क्षेत्रफल रेखा x = a द्वारा दो बराबर भागों में विभाजित होता है तो a का मान ज्ञात कीजिए।
हल:
वक्र x = y² एक परवलय है, जिसका शीर्ष मूल बिन्दु है। y = 0 इसका अक्ष है। जिसके सापेक्ष परवलय सममित हैं तथा x = 4 एक सरल रेखा है जो ‘-अक्ष से 4 इकाई दूरी पर है।

प्रश्न 9.
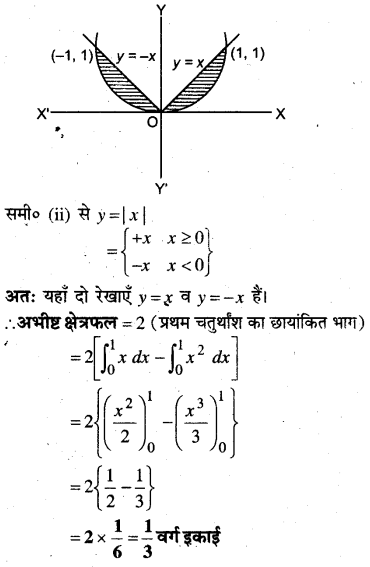
परवलय y = x² एवं y = |x| से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
दिया है y = x² ….(i)
और y = |x|
समी० (i) से स्पष्ट है कि यह एक परवलय का समी० है जिसका केन्द्र मूल बिन्दु है।

प्रश्न 10.
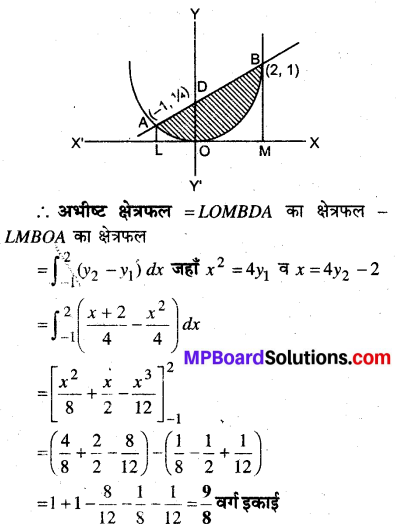
वक्र x² = 4y एवं रेखा x = 4y – 2 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
वक्र का समी० x² = 4y …(i)
तथा रेखा का समी० x = 4y – 2 …(ii)
समी० (i) व (ii) को हल करने पर वक्र तथा रेखा के प्रतिच्छेदन बिन्दु (2, 1) और (-1, 1/4) प्राप्त होते हैं।
वक्र एक ऊपरी ओर का परवलय हैं जिसका केन्द्र मूल बिन्दु हैं।

प्रश्न 11.
वक्र y² = 4x एवं रेखा x = 3 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
वक्र का समी० y² = 4x …(i)
रेखा का समी० x = 3 …(ii)

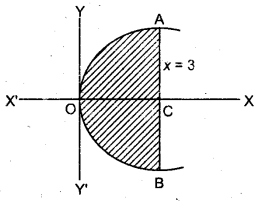
समी० (i) एक परवलय का समी० है जिसका केन्द्र मूल बिन्दु है।
तथा x = 3 रेखा है जो -अक्ष के समान्तर 3 इकाई दूरी पर है।
अभीष्ट क्षेत्रफल OBCAO का क्षेत्रफल
= 2 × OBCAO का क्षेत्रफल

प्रश्न 12 व 13 में सही उत्तर का चयन कीजिए
प्रश्न 12.
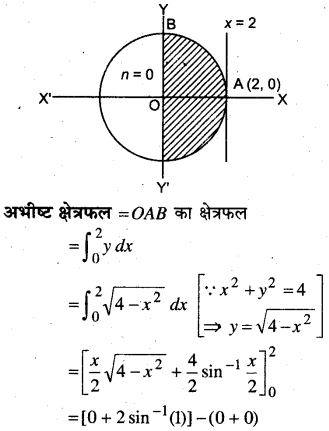
प्रथम चतुर्थांश में वृत्त x² + y² = 4 एवं रेखाओं x = 0, x = 2 से घिरे क्षेत्र का क्षेत्रफल है-
(A) π
(B) \(\frac{\pi}{2}\)
(C) \(\frac{\pi}{3}\)
(D) \(\frac{\pi}{4}\)
हल:
वृत्त का समी० x² + y² = 4

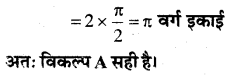
प्रश्न 13.
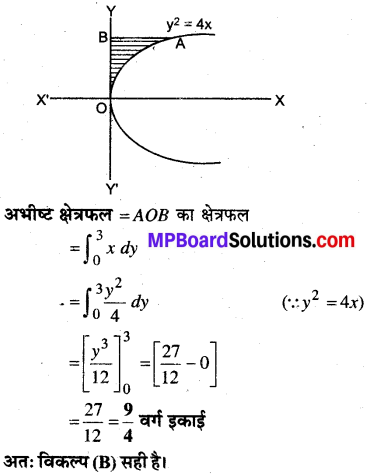
वक्र y² = 4x, y-अक्ष एवं रेखा y = 3 से घिरे क्षेत्र का क्षेत्रफल है-
(A) 2
(B) \(\frac{9}{4}\)
(C) \(\frac{9}{3}\)
(D) \(\frac{9}{2}\)
हल:
वक्र का समी० y = 4x
यह एक परवलय का समी० है जिसका केन्द्र मूल बिन्दु है।