In this article, we share MP Board Class 12th Maths Book Solutions Chapter 7 समाकलन Ex 7.10 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Book Solutions Chapter 7 समाकलन Ex 7.10
1 से 8 तक के प्रश्नों में समाकलनों का मान प्रतिस्थापन का उपयोग करते हुए ज्ञात कीजिए-
प्रश्न 1.
\(\int_{0}^{1} \frac{x}{x^{2}+1} d x\)
हल:

प्रश्न 2.
\(\int_{0}^{\pi / 2} \sqrt{\sin \phi} \cos ^{5} \phi d \phi\)
हल:
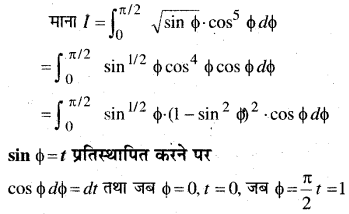

प्रश्न 3.
\(\int_{0}^{1} \sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right) d x\)
हल:
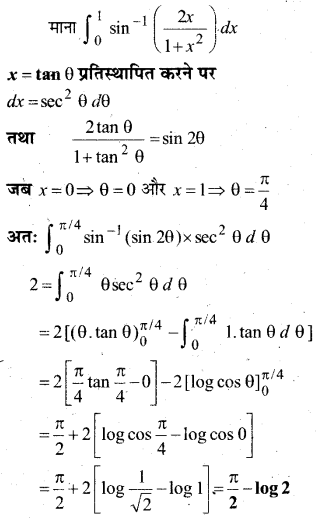
प्रश्न 4.
\(\int_{0}^{2} x \sqrt{x+2} d x\)
हल:
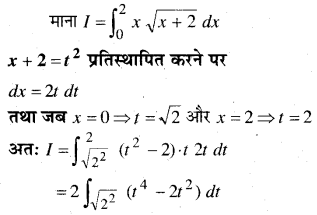

![]()
प्रश्न 5.
\(\int_{0}^{\pi / 2} \frac{\sin x}{1+\cos ^{2} x} d x\)
हल:

प्रश्न 6.
\(\int_{0}^{2} \frac{d x}{x+4-x^{2}}\)
हल:
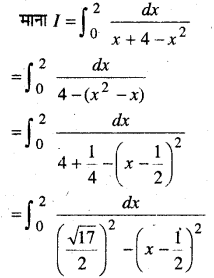

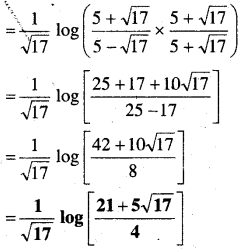
प्रश्न 7.
\(\int_{-1}^{1} \frac{d x}{x^{2}+2 x+5}\)
हल:
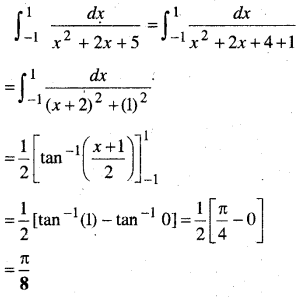
प्रश्न 8.
\(\int_{1}^{2}\left(\frac{1}{x}-\frac{1}{2 x^{2}}\right) e^{2 x} d x\)
हल:

![]()
प्रश्न 9 एवं 10 में सही उत्तर का चयन कीजिए
प्रश्न 9.
समाकलन \(\int_{1 / 3}^{1} \frac{\left(x-x^{3}\right)^{1 / 3}}{x^{4}} d x\) का मान है-
(A) 6
(B) 0
(C) 3
(D) 4
हल:
x = sin θ रखने पर
dx = cos θ dθ
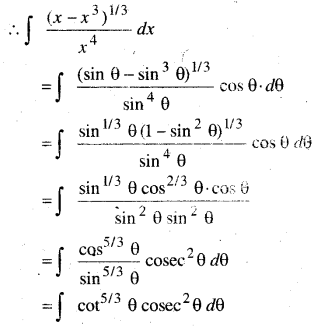
पुनः cot θ = t प्रतिस्थापित करने पर
-cosec2θ dθ = dt

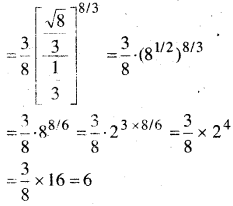
अतः विकल्प (A) सही है।
प्रश्न 10.
यदि f(x) = \(\int_{0}^{x} t \sin t d t\) है, तब f'(x) है-
(A) cos x + x sin x
(B) x sin x
(C) x cos x
(D) sin x + x cos x
हल:
f(x) = \(\int_{0}^{x} t \sin t d t\)
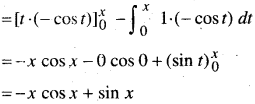
अतः f'(x) = -[cos x – x sin x] + cos x
= – cos x + x sin x + cos x
= x sin x
अतः विकल्प (B) सही है।