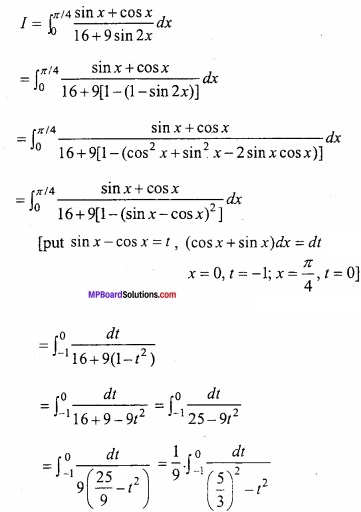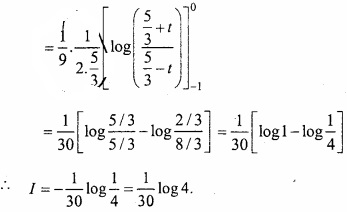MP Board Class 12th Maths Important Questions Chapter 7B Definite Integral
Definite Integral Important Questions
Definite Integral Long Answer Type Questions – II
Question 1.
Evaluate \(\int_{0}^{4 a} \frac{f(x)}{f(x)+f(4 a-x)} d x\)?
Solution:
Let

Adding eqns.(1) and (2),

![]()
Question 2.
Prove that \(\int_{\pi / 6}^{\pi / 3} \frac{d x}{1+\sqrt{\tan x}}=\frac{\pi}{12}\)? (NCERT)
Solution:

Adding eqns.(1) and (2),

Question 3.
Evaluate \(\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} e^{x}(\log \sin x+\cot x) d x\)?
Solution:
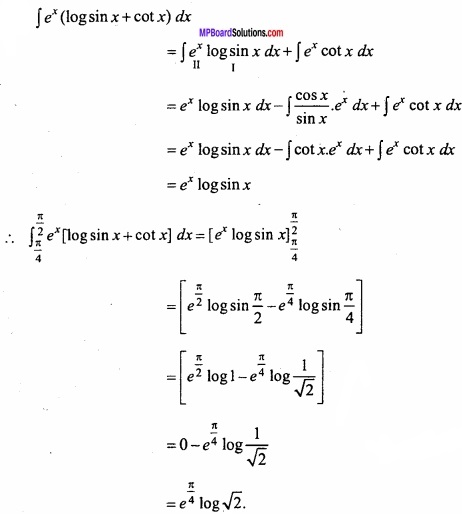
Question 4.
Evaluate \(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}|2 \sin | x|+\cos | x|| d x\)?
Solution:
Let

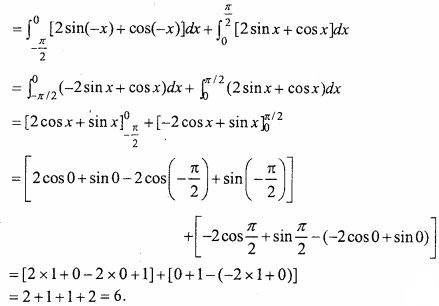
![]()
Question 5.
Prove that:
\(\int_{0}^{\pi} \frac{x \tan x}{\sec x+\cos x} d x=\frac{\pi^{2}}{4}\)?
Solution:

Adding eqns. (1) and (2)

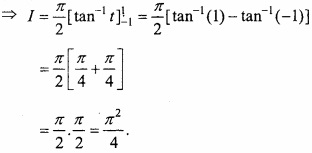
Question 6.
Prove that:
\(\int_{0}^{\pi / 2} \frac{x \sin x \cos x}{\cos ^{4} x+\sin ^{4} x} d x=\frac{\pi^{2}}{16}\)?
Solution:
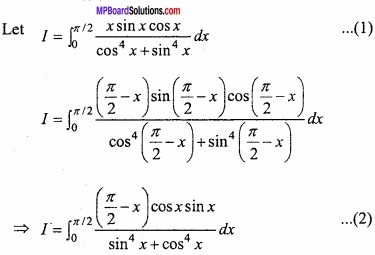
Adding eqns.(1) and (2)
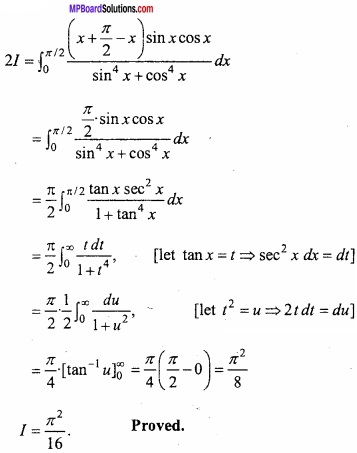
Question 7.
Prove that:
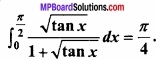
Solution:
Let
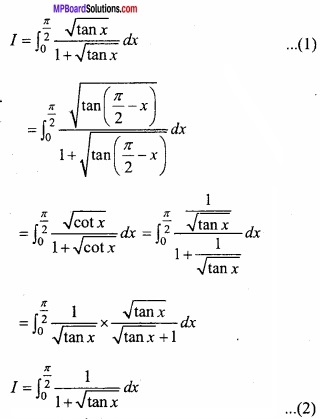
Adding eqns. (1) and (2)

Question 8.
Prove that:

Solution:
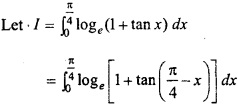

Question 9.
Evaluate
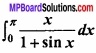
Solution:
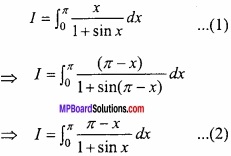
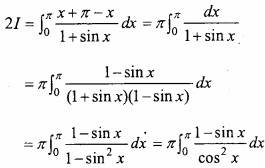
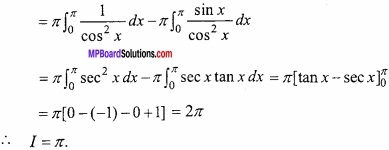
![]()
Question 10.
Prove that:
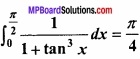
Solution:

Adding eqns.(1) and (2),

Question 11.
Evaluate
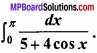
Solution:
Let
![]()

When x = 0, then t = tan 0 = 0
and when x = π, then t = tan \(\frac { \pi }{ 2 } \) = ∞
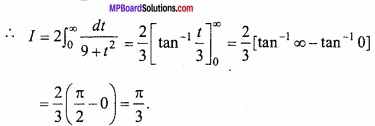
![]()
Question 12.
Prove that:
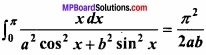
Solution:
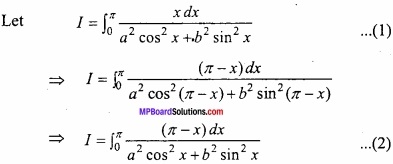
Adding eqns. (1) and (2)
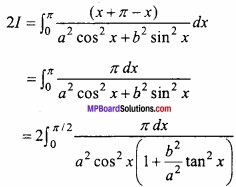

Question 13.
Prove that:
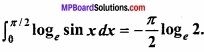
Solution:
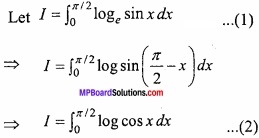
Adding eqns. (1) and (2)
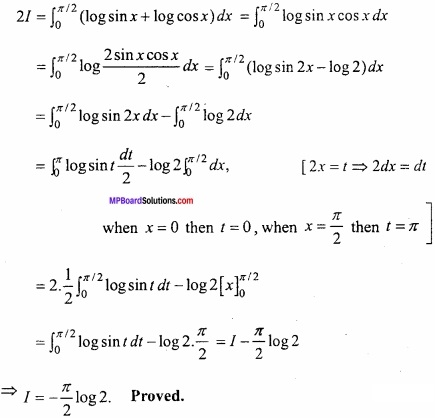
![]()
Question 14.
Prove that:
![]()
Solution:

Question 15.
Evaluate
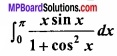
Solution:
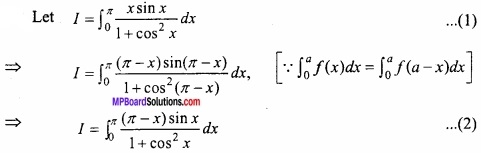
Adding eqns.(1) and (2)

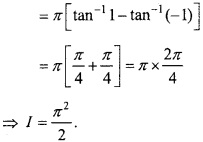
![]()
Question 16.
Evaluate

Solution:
Let