MP Board Class 12th Maths Important Questions Chapter 8 Application of Integrals

MP Board Class 12th Maths Important Questions Chapter Application of Integrals

Application of Integrals Important Questions

Application of Integrals Objective Type Questions

Question 1.
Choose the correct answer:

Question 1.
The value of \(\int_{0}^{\frac{\pi}{2}} \frac{\sin x}{\sin x+\cos x} d x\) is:
(a) π
(b) \(\frac { \pi }{ 2 } \)
(c) \(\frac { \pi }{ 4 } \)
(d) \(\frac { -\pi }{ 4 } \)
Answer:
(c) \(\frac { \pi }{ 4 } \)

Question 2.
Area of the best quadrant of the ellipse \(\frac { x^{ 2 } }{ a^{ 2 } } \) + \(\frac { y^{ 2 } }{ b^{ 2 } } \) = 1 is:
(a) πab
(b) \(\frac{1}{2}\) πab
(c) \(\frac{1}{4}\) πab
(d) \(\frac{1}{8}\) πab
Answer:
(c) \(\frac{1}{4}\) πab

Question 3.
The value of \(\int_{2}^{4} x^{3} d x\) is:
(a) 60
(b) 50
(c) 70
(d) 256
Answer:
(a) 60

Question 4.
\(\int_{0}^{2 a} f(x) d x=0\), if:
(a) f(2a – x) = f(x)
(b) f(2a – x) = – f(x)
(c) f(x) is an even function
(d) f(x) is an odd function
Answer:
(b) f(2a – x) = – f(x)

Question 5.
The value of \(\int_{0}^{2 \pi}|\sin x| d x\) is equal to:
(a) 2
(b) \(\sqrt{3}\)
(c) 4
(d) 0
Answer:
(d) 0

Question 2.
Fill in the blanks:

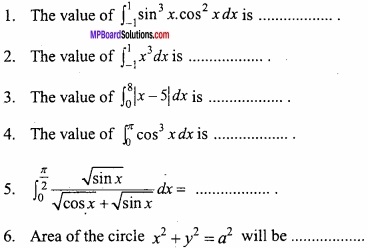
Answer:

1. 0
2. 0
3. 17
4. 0
5. \(\frac { \pi }{ 4 } \)
6. πa²

Question 3.
Write True/False:

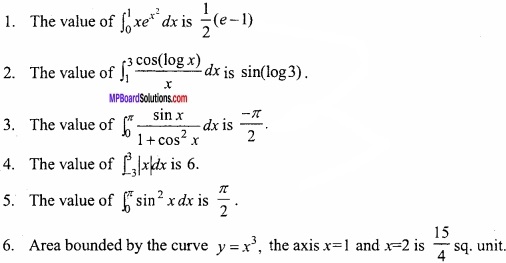
Answer:

1. True
2. True
3. False
4. False
5. True
6. True

Question 4.
Match the column:

Answer:

1. (b)
2. (a)
3. (d)
4. (c)
5. (f)
6. (e)

Question 5.
Write the answer in one word/sentence:

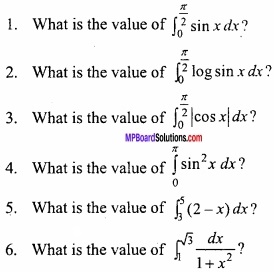
Answer:

1. 1
2. \(\frac { -\pi }{ 2 } \) log 2
3. 2
4. \(\frac { \pi }{ 2 } \)
5. -4
6. \(\frac { \pi }{ 12 } \)

Application of Integrals Long Answer Type Questions – II

Question 1.
Find the area bounded by the parabolas x² = 8y and y² = 8x?
Solution:
Equation of given parabolas:
x² = 8y ………………. (1)
and y² = 8x ………………….. (2)
Solving eqns. (1) and (2),

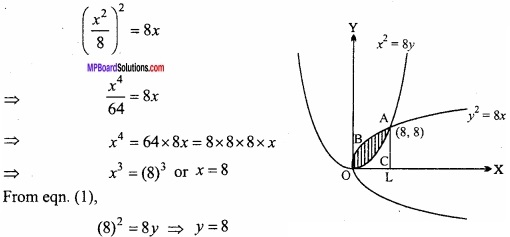
Coordinate of A(8, 8)
Two parabolas intersect at point O and A.
∴ Required area = Area OBALO – Area OCALO

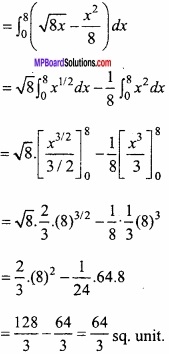
Question 2.
Find the area bounded by the curve y = cos x, the X – axis and x = 0, x = 2π, by integration method?
Solution:
y = f(x) = cos x
When x ∈ [0, \(\frac { \pi }{ 2 } \), cos x ≥ 0;
x ∈ [0, \(\frac { \pi }{ 2 } \), [0, \(\frac { 3\pi }{ 2 } \), cos x ≤ 0;
When x ∈ \(\frac { 3\pi }{ 2 } \), 2π] cos x ≥ 0

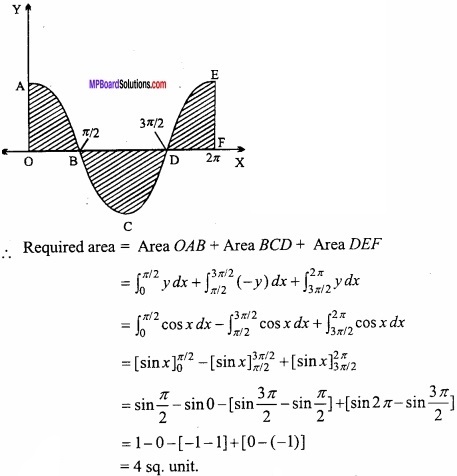
Question 3.
(A) Find the area between the curves y² = 4x and y = 2x? (Integral method)
Solution:
Given, Curve and line are y² = 4x and – y = 2x
(2x)² = 4x
⇒ 4x² = 4x
⇒ x² – x = 0
⇒ x (x – 1) = 0
∴ x = 0 or x = 1
Then y = 2x = 0 or y = 2 × 1 = 2

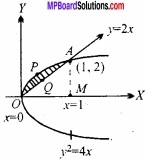
The point of intersections of curve and line are (0, 0) and (1,2).
Area of shaded region = ar (OPAMO) – ar (OQAMO)

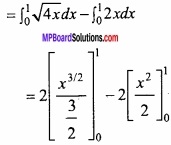
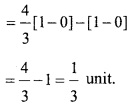
(B) Find the area bounded by the curves x² = 4y and x = 4y – 2 by integration method?
Solution:
Given, Curve and line are y² = 4x and – y = 2x
(2x)² = 4x
⇒ 4x² = 4x
⇒ x² – x = 0
⇒ x (x – 1) = 0
∴ x = 0 or x = 1
Then y = 2x = 0 or y = 2 × 1 = 2

The point of intersections of curve and line are (0, 0) and (1,2).
Area of shaded region = ar (OPAMO) – ar (OQAMO)

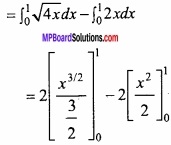
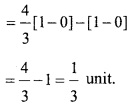
Question 4.
Find the area bounded by lines |x|+|y|= a by using integration method?
Solution:
The given lines are represented by |x|+|y| = a will be
x + y = a ……………. (1)
-x – y = a ……………………. (2)
x – y = a ……………………. (3)
and – x + y = a ………………… (4)
⇒ \(\frac { x }{ a } \) + \(\frac { y }{ a } \) = 1, \(\frac { x }{ -a } \) + \(\frac { y }{ -a } \) = 1
⇒ \(\frac { x }{ a } \) + \(\frac { y }{ -a } \) = 1, \(\frac { x }{ -a } \) + \(\frac { y }{ a } \) = 1

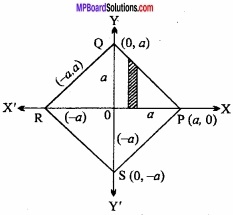
The above graph is represented by the PQ, RS, PS and QR respectively.
Hence, the area bounded by these lines
= 4 × ∆Area of OPQ

Question 5.
(A) Find the rea of circle x² + y² = a² by using integration method?
Solution:
Given:
x² + y² = a²
⇒ y² = a² – x²
⇒ y = \(\sqrt { a^{ 2 }-x^{ 2 } } \)
The circle is symmetric about the axes
Area = 4 × area of quadrant OAB

(B)
Find the area of the circle x² + y² = 25 by using integration method?
Solution:
Solve as Q. No. 5 (A) by putting a = 5.

Question 6.
Find the area included between two parabolas:
y² = 4 ax and x² = 4ay, a > 0.
Solution:
The equations of the given parabolas are
y² = 4ax.
and x² = 4ay
Putting the value of y from eqn. (2) in eqn. (1), we have

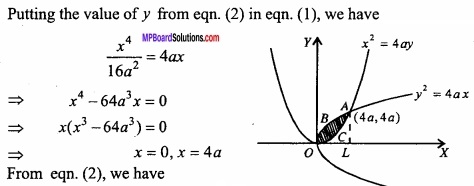
From eqn.(2), we have
y = 0, y = \(\frac { (4a)^{ 2 } }{ 4a } \) = 4a
∴The points of intersection of the given parabolas are (0, 0) and (4a, 4a).
Now, Required area = Area OBAL – Area OCAL

Question 7.
Find the area enclosed between parabolas y² = 4x and x² = 4y?
Solution:
y² = 4x ……………… (1)
x² = 4y …………………. (2)
Putting the value of y in eqn.(1), we get

∴ At O, x = 0 and at M, x = 4
Hence Required area Area OAPB O
= Area OAPMO – Area OBPMO

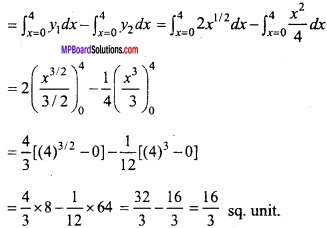
Question 8.
Find the area between curve y² = x and x² = y by integral method?
Solution:
Solve as Q.No. 7.

Question 9.
Find the area enclosed by the ellipse \(\frac { x^{ 2 } }{ a^{ 2 } } \) + \(\frac { y^{ 2 } }{ b^{ 2 } } \) = 1?
Solution:
Equation of the ellipse is

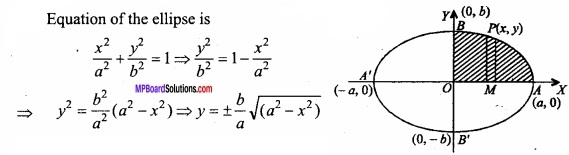
∴ Required area = 4 area AOB

Question 10.
Find the area of the region bounded by the parabola y² = 4ax and its latus rectum?
Solution:
Equation of the parabola is
y² = 4ax or y = ±2 \(\sqrt { ax } \)
In the figure, LSL’ is latus rectum and vertex is O (0, 0)
∴ Required area = 2 × Area OSL

Question 11.
Find the area enclosed between parabola y² = 4ax and straight line y = mx?
Solution:
Equation of the parabola y² = 4ax ……………. (1)
Equation of straight line y = mx ………………….. (2)
O is the origin (O, O). P is the point of intersection of parabola and the straight line. Solving eqns. (1) and (2) we get,
y² = 4ax
⇒ (mx)² = 4ax
⇒ m²x² – 4ax = 0
⇒ x(m² – 4a) = 0
∴ x = 0, x = \(\frac { 4a }{ m^{ 2 } } \)

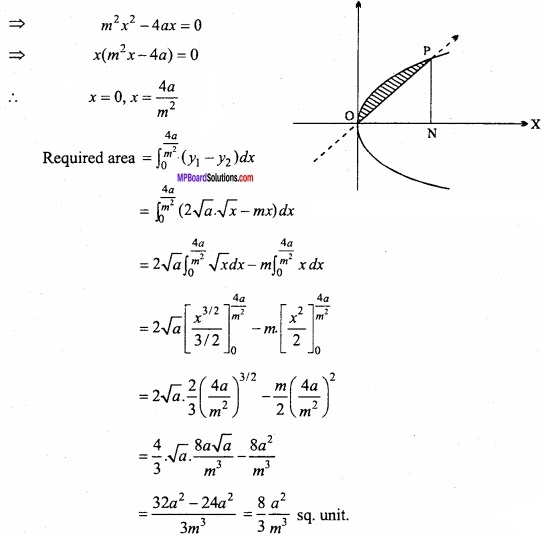
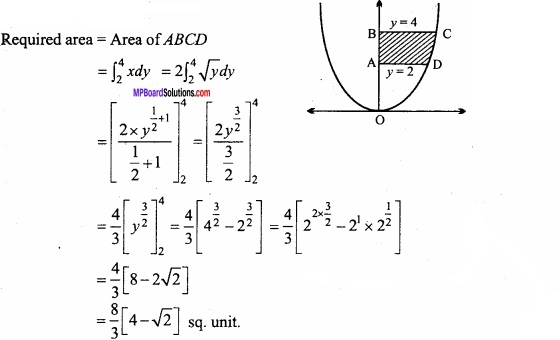
Question 12.
Find the area bounded by the curve x² = 4y, y = 2, y = 4 and Y – axis in the first quadrant? (NCERT)
Solution:
Given equation of curve is:
x² = 4y
⇒ x = \(2\sqrt { y } \)
Required area = Area of ABCD

Question 13.
Find the area of the smaller part of the circle x² + y² = a² cut off by the line x = \(\frac { a }{ \sqrt { 2 } } \)? (NCERT)
Solution:
Given equation of curve is:
x² + y² = a² …………………………. (1)
⇒ y² = a² – x²
⇒ y = \(\sqrt { a^{ 2 }-x^{ 2 } } \)
Equation of line is:


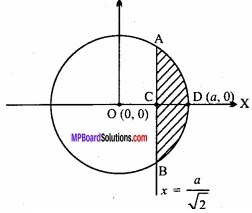
Point of intersection of circle and line is A \(\frac { a }{ \sqrt { 2 } } \), \(\frac { a }{ \sqrt { 2 } } \)
Coordinates of D is (a, 0).
∴ Required area = Area of ABD

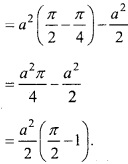
Question 14.
The area between x = y² and x = 4 is divided into two equal parts by the line x = a. Find the value of a? (NCERT)
Solution:
Given:
Equation of parabola is
x = y²
⇒ y = \(\sqrt{x}\)
Area bounded by the parabola and the line x = 4 is divided into two equal parts by the line x = a.
Area OEC = Area EFCB

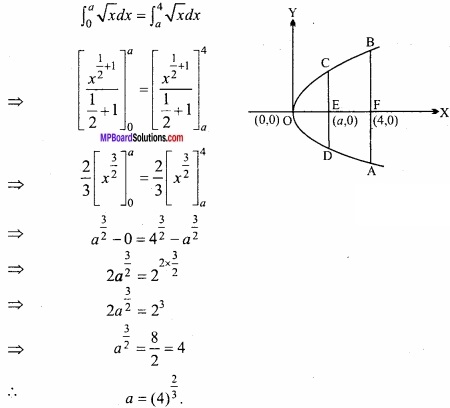
Question 15.
Find the area lying in the first quadrant and bounded by the circle x² + y² = 4 and the lines x = 0 and x = 2? (NCERT)
Solution:
Given equation of circle is:
x² + y² = 4
⇒ y² = 4 – x²
⇒ y = \(\sqrt { (2)^{ 2 }-x^{ 2 } } \)

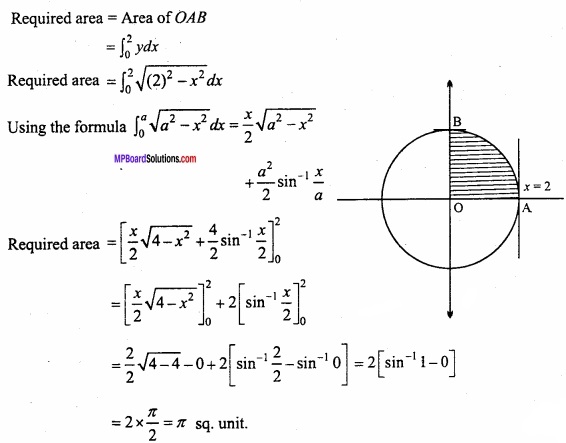
Question 16.
Find the area enclosed by a circle x² + y² = 32, a line y = x and axis of A in the first quadrant?
Solution:
Equation of circle is:

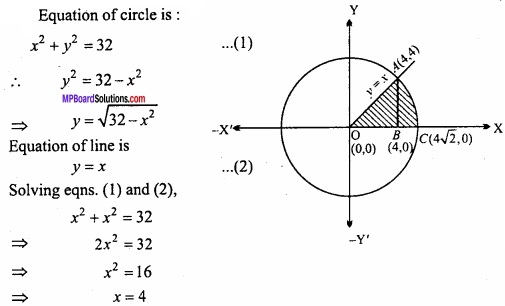
Putting the value of x in eqn. (2)
y = 4
The point of intersection of the line and circle are 0(0,0) and A(4,4) coordinates of B are are (4,0) and coordinates of C are (4\(\sqrt{2}\),0).
Required area = Area OACBO
= Area OAB + Area ABC

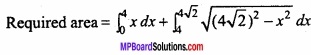
Question 17.
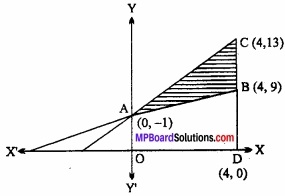
Find the area of triangle whose sides are y = 2x + 1, y = 3x +1 and x = 4? (NCERT)
Solution:
Let the equation of sides AB,AC and BC of & ABC ore respectively.
y = 2x + 1 …………… (1)
y = 3x + 1 ………….. (2)
and x = 4 …………….. (3)
By solving eqns. (1) and (2) we have A (0, 1), by solving eqns. (1) and (3) we have B (4, 9) and by solving eqns. (2) and (3) we have C (4, 13).
Thus required area

MP Board Class 12 Maths Important Questions