MP Board Class 12th Maths Important Questions Chapter 6 Application of Derivatives
Application of Derivatives Important Questions
Application of Derivatives Objective Type Questions:
Question 1.
Choose the correct answer:
Question 1.
The rate of change of the area of a circle with respect to its radius r when r = 5 is:
(a) 10 π
(b) 12 π
(c) 8 π
(d) 11 π.
Answer:
(b) 12 π
Question 2.
Tangent line of a curve y2 = 4x at y = x + 1 is:
(a) (1,2)
(b) (2, 1)
(c) (1, -2)
(d) (- 1, 2).
Answer:
(a) (1,2)
Question 3.
Approximate change in the volume of a cube of side x metre caused by increasing the side by 2%:
(a) 0.03 x3
(b) 0.02 x3
(c) 0.06 x3
(d) 0.09 x3
Answer:
(c) 0.06 x3
![]()
Question 4.
Point on the curve x2 = 2y which lie minimum distance from the point (0,5):
(a) (2\(\sqrt{2}\),4)
(b) (2\(\sqrt{2}\),0)
(c) (0, 0)
(d) (2, 2).
Answer:
(a) (2\(\sqrt{2}\),4)
Question 5.
Minimum value of the function f(x) = x4 – x2 – 2x + 6:
(a) 6
(b) 4
(c) 8
(d) None of these.
Answer:
(b) 4
Question 2.
Fill in the blanks:
- The function f(x) = cosx, for 0 ≤ x ≤ π is …………………………..
- The radius of circular plate is increasing at the rate of 0.2 cm /sec. when r = 10, then the rate of change of the area of the plate is ………………………………
- The function y = x(5 – x) is maximum at x is equal to ……………………………
- The minimum value of 2x + 3y is ………………………….. when xy = 6.
- The maximum value of sin x + cos x is ……………………………
- If line y = mx+ 1 is a tangent line to the curve y2 = 4x. Then value of m will be ……………………………..
- Slope of the tangent to the curve y = x2 at the point (1, 1) is ………………………….
- Using differential the approximate value of \(\sqrt{0.6}\) is …………………………….
Answer:
- Decreasing
- 4πcm2/sec
- \(\frac{5}{2}\)
- 12
- \(\sqrt{2}\)
- 1,
- 2,
- 0.8.
![]()
Question 3.
Write True/False:
- For all real values of x, the function f(x) = ex – e-x is increasing function.
- If the length of equal sides of an isosceles traingle be x then its maximum area will be \(\frac{1}{2}\) x2
- Function f(x) = 3x2 – 4x is increasing in the interval (- ∞, \(\frac{2}{3}\) )
- Function f(x) = x – cot x is always decreasing.
- Equation of the normal of the curve y = ex at point (0, 1) is x + y = l.
Answer:
- True
- True
- False
- False
- True.
Application of Derivatives Short Answer Type Questions
Question 1.
The radius of a circle increases at the rate of 2cm/sec. At what rate the area increases when radius is 10cm?
Solution:
Given:
\(\frac { dr }{ dt } \) = 2cm/sec
Let the area of circle be A
Then,

∵ Area of circle A = πr2

= 40π sq.cm/second
![]()
Question 2.
The radius of air bubble is increasing at the rate of 1/2 cm per second. At what rate the volume of the air bubble is increasing when the radius is 1 cm?
Solution:
Let the radius of air bubble be r.
∴ Volume V = \(\frac{4}{3}\) πr3

Question 3.
The radius of a balloon is increasing at the rate of 10 cm/sec? At what rate surface area of the balloon is increasing when radius is 15cm?
Solution:
Let r be the radius of balloon at any time t and its surface be x then
A = 4πr2
Differentiating eqn.(1) w.r.t. t,

Hence, when radius of ballon is 15cm, then its area is increasing at rate of 1200π cm/sec.
Question 4.
Find those intervals in which the function f(x) = 2x3 – 15x2 + 36x + 1 is increasing or decreasing?
Solution:
f(x) = 2x3 – 15x2 + 36x + 1
⇒ f'(x) = 6x2 – 30x + 36
= 6(x2 – 5x + 6)
= 6(x – 2) (x – 3)
For increasing function of f(x),
f'(x) > 0
or (x – 2) (x – 3) > 0
⇒ x – 2 > 0 and x – 3 > 0
⇒ x > 2 and x < 3 ⇒ x > 3
Clearly the function is increasing in interval (3, ∞)
Again, (x – 2) (x – 3) > 0
or x – 2 < 0 and x – 3 < 0
⇒ x < 2 and x < 3
⇒ x < 2
Clearly the function is increasing in interval (-∞, 2)
Hence, the function is increasing in the interval (-∞, 2) ∪ (3, ∞)
Again for decreasing function of f(x),
f'(x) < 0
⇒ (x – 2) (x – 3) < 0
or x – 2 < 0 and x – 3 > 0
⇒ x < 2 and x > 3, which is impossible
or x – 2 > 0 and x – 3 < 0 ⇒ x > 2 and x < 3
⇒ 2 < x < 3
Hence, f(x) is decreasing function in the interval (2, 3).
![]()
Question 5.
(A) If x + y = 8, then find maximum value of xy?
Solution:
Let P = xy
⇒ x + y = 8
⇒ y = 8 – x
∴P = x(8 – x) = 8x – x2
⇒ \(\frac { dP }{ dx } \) = 8 – 2x
⇒ \(\frac { d^{ 2 }P }{ dx^{ 2 } } \) = -2
For maximum or minimum value
8 – 2x = 0
⇒ x = 4
Now, x = 4 then \(\frac { d^{ 2 }P }{ dx^{ 2 } } \) = -2, which is negative
∴ at x = 4, then y = 4
Maximum value of P, when x = 4, y = 4
= 4 × 4 = 16.
(B) If x + y = 10 then find maximum value of xy?
Solution:
Solve like Q.No.5(A).
Question 6.
The radius of a circle increases at the rate of 3cm/sec. At what rate the area increases when the radius is 10cm?
Solution:
Let r be the radius and A be the area of circle then,
A = πr2
\(\frac { dA }{ dt } \) = rate of change of area = ?
⇒ \(\frac { dA }{ dt } \) = 2πr \(\frac { dr }{ dt } \)
⇒ \(\frac { dA }{ dt } \) = 2π.(10).3
= 60π cm2/second.
![]()
Question 7.
The volume of a cube is increasing at the rate of 9 cm3/sec? If the edge of cube is 10cm then at what rate the surface area of cube is increasing? (NCERT)
Solution:
Let the edge of cube = a dm
Volufne = V= a3
Surface area of cube = s = 6a2
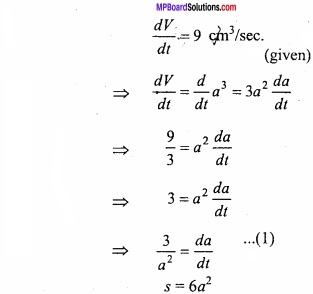
Surface area of cube

When a = 10cm, then \(\frac { ds }{ dt } \) = \(\frac { 36 }{ 10 } \) = 3.6 cm2/sec.
Question 8.
(A) A man 180 cm high walks away from a lamp post at a rate of 1.2metre per second. If the height of lamp post is 4.5 metre. Find the rate at which the length of his shadow increases?
Solution:
Let AB be the lamp post of the height 4.5 m, PQ be the position of man at time t, CQ = x and BQ = y
drrf
(B) A man of height 2 metre walking away from a lamp post at a rate of 5km/ sec. If the height of the lamp post 6m. Find the rate at which the length of his shadow is increasing? (NCERT)
Solution:
Solve like Q. No.8(A).
[Ans. \(\frac{5}{8}\) km/sec.]
Question 9.
A ladder 5 metre long is leaning against a wall. The bottom of the ladder is pulled along the ground away from the wall, at the rate of 2 metre per second. How just is its height on the wall decreasing when the foot of the ladder is 4 metre away from the wall? (NCERT)
Solution:
Let at any time t, the bottom of the ladder be at a distance x metre from the wall and the height of the wall bey metre.
QA = xm, OB = ym, AB = 5m (given)
\(\frac { dx }{ dt } \) = 2m/sec.
In ∆OAB,
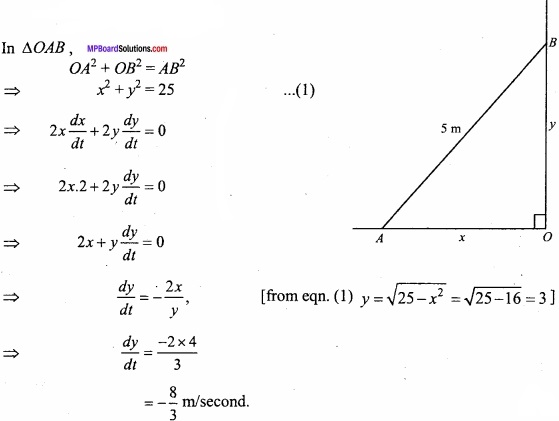
Question 10.
Find the intervals in which f(x) = 5x3 + 7x – 13 is increasing or decreasing?
Solution:
Given:
f(x) = 5x2 + 7x – 13 (given)
∴ f'(x) = 10x + 7
If f(x) is increasing,
f'(x) > 0
⇒ 10x + 7 > 0
⇒ x > \(\frac{-7}{10}\)
Hence, f(x) is increasing in interval ( \(\frac{-7}{10}\) , ∞)
If f(x) os decreasing, then,
f'(x) < 0
⇒ 10x + 7 < 0
⇒ x < \(\frac{-7}{10}\)
∴ f(x) is decreasing in (-∞, \(\frac{-7}{10}\) ).
![]()
Question 11.
Find the intervals in which the function f(x) = 2x3 – 24x + 5 is increasing or decreasing?
Solution:
f(x) = 2x3 – 24x + 5
Differentiating w.r.t x,
f'(x) = 6x2 – 24
⇒ f'(x) = 6(x2 – 4)
⇒ f'(x) = 6(x + 2) (x-2) …………………. (2)
(A) If f(x) in is increasing, then
f'(x) > 0
6(x + 2)(x-2) > 0
∴ f(x), x ∈ (-∞,-2) ∪(2, ∞) is increasing.
(B) If f(x) is decreasing,
f'(x) < 0 ⇒ 6(x + 2) (x – 2) < 0
f(x), x ∈ (-2,2) decreasing.
Question 12.
Show that the function f(x) = x – cos x is always increasing?
Solution:
Given function f(x) = x – cos x
∴ f'(x) = 1 – (- sin x)
⇒ f'(x) = 1 + sin x
We know that -1 ≤ x ≤ 1
-1 + 1 ≤ 1 + sin x ≤ 1 + 1
0 ≤ 1 + sin x ≤ 2
Hence f'(x) = 1 + sin x is always positive for all values of x.
∴ f(x) = x – cos x is always increasing.
![]()
Question 13.
Find the least value of a such that the function given by f(x) = x2 + ax + 1 is strictly increasing on (1, 2)? (NCERT)
Solution:
Given:
f(x) = x2 + ax + 1
∴ f'(x) = 2x + a
When, x ∈ (1,2)
∴ 1 < x < 2
⇒ 2 < 2x < 4
⇒ 2 + a < 2x + a < A + a
⇒ 2 + a < f'(x) < 4 + a Since f(x) is increasing function ∴ f'(x) > 0
⇒ 2 + a > 0 ⇒ a > -2
Hence, the least value of a is -2.
Question 14.
Let I be any interval disjoint from [-1, 1] prove that the function f given by f(x) = x + \(\frac{1}{x}\) is strictly increasing on I? (NCERT)
Solution:
f(x) = x + \(\frac{1}{x}\)
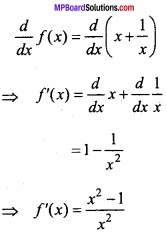
x ∈ 1, x ∉ (-1, 1)
x < – 1 0r x > 1
⇒ x2 – 1 > 0
⇒ \(\frac { x^{ 2 }-1 }{ x^{ 2 } } \) > 0
⇒ f'(x) > 0, x ∈ 1
∴ f(x) is increasing on I. Proved.
![]()
Question 15.
Find the interval in which the given function is increasing or decreasing:
f(x) = x4 – \(\frac { x^{ 3 } }{ 3 } \)?
Solution:
f(x) = x4 – \(\frac { x^{ 3 } }{ 3 } \)

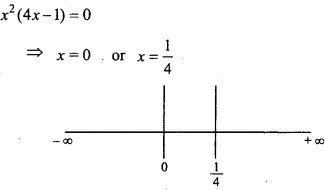
Hence, the interval 0 and \(\frac{1}{4}\) on X – axis is divided in three intervals
(- ∞, 0), (0, \(\frac{1}{4}\) ), ( \(\frac{1}{4}\), ∞)
In interval (- ∞, 0)
f'(x) = x2 (4x – 1),
⇒ f'(x) < 0 [x2 = +ve] [4x – 1 > 0]
⇒ f'(x) < 0
∴ In interval (- ∞, 0) the function f(x) decreasing
In interval (0, \(\frac{1}{4}\) ):
f'(x) = x2 (4x – 1),
⇒ f'(x) > 0 [∵ x2 = positive] [4x – 1 > 0]
∴ In interval (0, \(\frac{1}{4}\) ) f(x) is decreasing
In interval ( \(\frac{1}{4}\), ∞):
f'(x) = x2 (4x – 1), [∵ x2 = positive] [4x – 1 > 0]
⇒ f'(x) > 0
In interval ( \(\frac{1}{4}\), ∞) in function f(x) increasing.
![]()
Question 16.
The perimeter of a rectangle is 100 cm. Find the length of sides of the rectangle for maximum area?
Solution:
Let length of rectangle be x and breadth be y.
∴Perimeter of rectangle = 2(x + y)
⇒ 2x + 2y = 100
⇒ x + y = 50
Let area of rectangle,
A = xy = x(50 – x) = 50x – x2, [from eqn.(1)]
\(\frac { dA }{ dx } \) = 50 – 2x
and \(\frac { d^{ 2 }A }{ dx^{ 2 } } \) = -2
For maximum or minimum of A,
\(\frac { dA }{ dx } \) = 0
⇒ 50 – 2x = 0 or or x = 25
For any value of x, \(\frac { d^{ 2 }A }{ dx^{ 2 } } \) is -ve
For x = 25, area of rectangle is maximum
Put in eqn.(1),
y = 50 – x = 50 – 25 = 25.
![]()
Question 17.
Area of a rectangle is 25 sq.cm. Find its length and breadth when its perimeter is minimum?
Solution:
Let the length and breadth of rectangle be x and y units and A be the area.
xy = 25 ……………………….. (1)
Perimeter of rectangle,
P = 2(x + y)

For maximum or minimum \(\frac { dP }{ dx } \) = 0
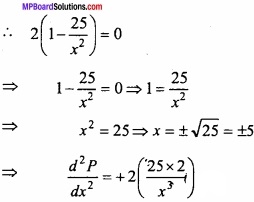
Which is positive for x = 5
∴ For Minimum parimeter x = cm.
y = \(\frac{25}{x}\) = \(\frac{25}{5}\) = 5 cm.
Question 18.
Find the maximum value of sin x + cos x = \(\sqrt{2}\)? (NCERT)
Solution:
Given:
f(x) = sin x + cos x …………………. (1)
∴f'(x) = cos x – sin x …………………… (2)
and f”(x) = – sinx – cos x …………………….. (3)
For maxima or minima
f'(x) = 0
∴ cos x – sin x = 0
⇒ sin x = cos x
⇒ tan x = 1
∴ x = \(\frac { \pi }{ 4 } \), \(\frac { 3\pi }{ 4 } \), \(\frac { 5\pi }{ 4 } \)
Put x = \(\frac { \pi }{ 4 } \) in eqn (3)
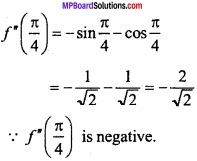
Hence, at x = \(\frac { \pi }{ 4 } \) the given function is maximum. In the same way for x = \(\frac { 3\pi }{ 4 } \), \(\frac { 5\pi }{ 4 } \) ………………… the function is maximum.
Put x = \(\frac { \pi }{ 4 } \) in eqn.(1),
Maximum value f ( \(\frac { \pi }{ 4 } \) ) = sin \(\frac { \pi }{ 4 } \) + cos \(\frac { \pi }{ 4 } \)
= \(\frac { 1 }{ \sqrt { 2 } } \) + \(\frac { 1 }{ \sqrt { 2 } } \) = \(\frac { 2 }{ \sqrt { 2 } } \) = \(\sqrt{2}\). Proved.
Question 19.
Two positive numbers are such that x +y = 60 and xy3 is maximum. Prove (NCERT)
Solution:
Given:
x + y = 60 …………………….. (1)
Let p = xy3
⇒ P = (60 – y). y3
⇒ P = 60y3 – y4
⇒ \(\frac{dp}{dy}\) = 180 y2 – 4y3 …………………….. (2)
Put \(\frac{dp}{dy}\) = 0
180 y2 – 4y2 = 0
⇒ 4y2 (45 – y) = 0
∴ y = 45
Differentiating eqn. (2) w.r.t y,
\(\frac { d^{ 2 }p }{ dy^{ 2 } } \) = 360y – 12y2
= 12 y(30 – y)
Put y = 45,
\(\frac { d^{ 2 }p }{ dy^{ 2 } } \) = 12 × 45 (30 – 45) = – ve
Hence, at y = 45, p is maximum
From eqn.(1),
x + 45 = 60
⇒ x = 15
∴ The two numbers are 15 and 45.
Question 20.
Find the slope of the tangent to curve y = x3 – x + 1 at the point whose x coordinate is 2? (NCERT)
Solution:
The equation of given curve,
y = x3 – x + 1

Slope of tangent at x = 2,

= 3 × 4 – 1 = 11.
Question 21.
Find the slope of the tangent to the curve y = \(\frac { x-1 }{ x-2 } \), x ≠ 2 at x = 10? (NCERT)
Solution:
The equation of given curve:
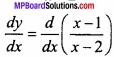
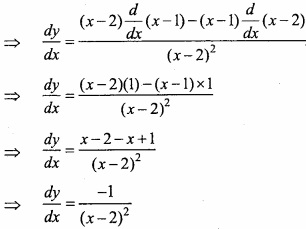
At x = 10 slope of tangent is:
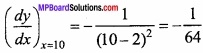
Question 22.
Find the point at which the tangent to curve y = x3 – 3x2 – 9x + 7 is parllel to X – axis? (NCERT)
Solution:
Equation of given curve y = x3 – 3x2 – 9x + 7
\(\frac { dy }{ dx } \) = \(\frac { d }{ dx } \) (x3 – 3x2 – 9x + 7)
⇒ \(\frac { dy }{ dx } \) = 3x2 – 6x – 9
= 3[x2 – 2x – 3]
= 3[x2 – 3x + x – 3]
= 3[x(x – 3) + 1(x – 3)]
⇒ \(\frac { dy }{ dx } \) = 3(x – 3) (x + 1)
Tangent is parllel to X – axis.
∴\(\frac { dy }{ dx } \) = 0
3 (x – 3) (x + 1) = 0
⇒ x = 3,-1
When x = 3, then y = (3)3 – 3(3)2 – 9 × 3 + 7
y = 27 – 27 – 27 + 7
y = – 20
When x = 3, then y = (-1)3 – 3(-1)2 – 9(-1) + 7
y = – 1 – 3 + 9 + 7
y = 12
Hence, the point at which the tangent is parllel to X – axis are (3, -20) and (-1, 12).
![]()
Question 23.
Find the equation of the tangent to the parabolas y2 = 4ax at the point (at2, 2at)? (NCERT)
Solution:
Given:
y2 = 4ax ……………………. (1)
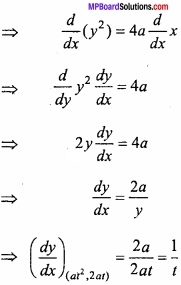
Equation of tangent is:
y – y1 = \(\frac { dy }{ dx } \) (x – x1)
Where x1 = at2, y1 = 2at, \(\frac { dy }{ dx } \) = \(\frac { 1 }{ t } \)
y – 2at = \(\frac { 1 }{ t } \) (x – at2)
⇒ yt – 2at2 = x – at2
⇒ x – ty + at2 = 0.
Question 24.
Find the equation of the tangent to the curve x2/3 + y2/3 = 2 at point (1, 1)? (NCERT)
Solution:
Equation of curve:
x2/3 + y2/3 = 2
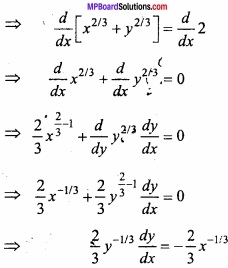
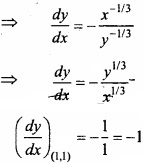
Equation of tangent at point (x1, y1) is:
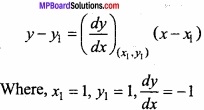
y – 1 = – (x – 1)
⇒ y – 1 = – x + 1
⇒ x + y – 2 = 0
Question 25.
Find the equation of tangent to the curve 2y + x2 = 3 at point (1, 1)? (NCERT)
Solution:
Equation of given curve:
2y + x2 = 3
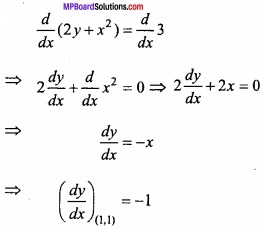
Equation of tangent at point (x1, y1) is:

⇒ y – 1 = x – 1
⇒ x – y = 0.
Question 26.
(A) Find the equation of tangent to the cure x = cos t, y = sin at t = \(\frac { \pi }{ 4 } \)? (NCERT)
Solution:
Equation of 1st curve:
x = cos t
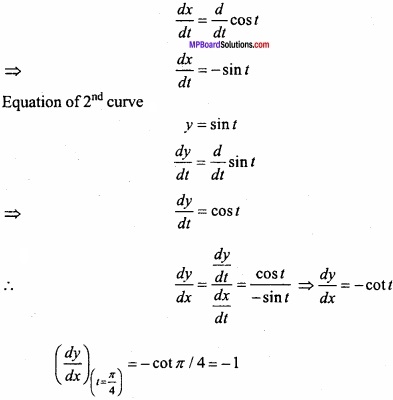
x = cos t = cos \(\frac { \pi }{ 4 } \) = \(\frac { 1 }{ \sqrt { 2 } } \)
y = sin t = sin \(\frac { \pi }{ 4 } \) = \(\frac { 1 }{ \sqrt { 2 } } \)
Equation of tangent at (x1, y1) is:
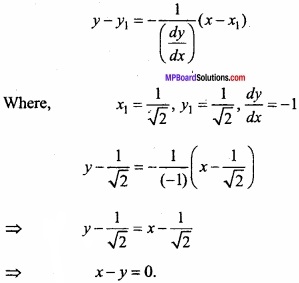
(B) Find the equation of tangent and normal to the curve 16x2 + 9y2 = 145 at point (x1, y1), where x1 = 2 and y1 > 0? (CBSE 2018)
Solution:
Given:
16x2 + 9y2 = 145 ……………………. (1)
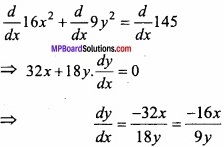
Put x = 2 in eqn.(1), we get
16.(2)2 +9y2 =145
⇒ 64 + 9y2 =145
⇒ 9y2 = 145 – 64 = 81
⇒ y2 =9, [y ≠ -3 ∵ y1 > 0]
⇒ y = 3
At point (2, 3)
\(\frac { dy }{ dx } \) = – \(\frac { 16 }{ 9 } \). \(\frac { 2 }{ 3 } \) = – \(\frac { 32 }{ 27 } \)
Equation of tangent of curve (1) at point (2, 3),

and equation of normal of curve (1) at point (2, 3) is,
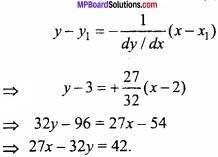
Question 27.
Use differential to approximate (25)1/3? (NCERT)
Solution:
Let y = x1/3
Where, x = 27 and ∆x = -2

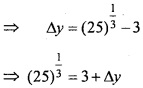
∆y is appromimately equal to dy.
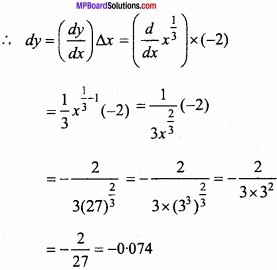
Approximately value of (25)1/3
= 3 + ∆y
= 3 – 0.074 = 2.926.
Question 28.
Use differential to approximate \(\sqrt { 36.6 } \)? (NCERT)
Solution:
Let y = \(\sqrt{x}\), where x = 36 and ∆x = 0.6
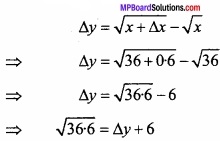
∆y is appromimately equal to b,
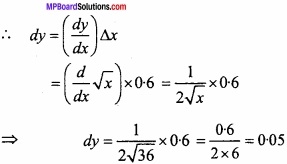
Approximate value of \(\sqrt { 36.6 } \)
= ∆y + 6
= 0.05 + 6 = 6.05
Question 29.
Use differential to approximate (15)1/4? (NCERT)
Solution:
Let y = x1/4
Where, x = 16 and ∆x = -1
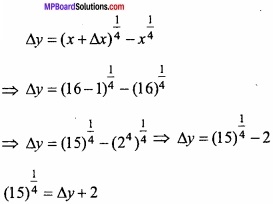
∆y is appromimately equal to dy,
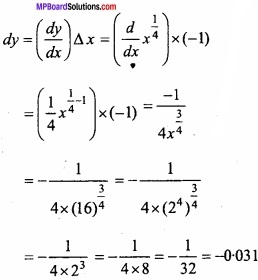
Approximately value of (15)1/4
∆y + 2 = 2 – 0.031 = 1.969.
Question 30.
Use differential to approximate (26)1/3? (NCERT)
Solution:
Let y = x1/3
Where, x = 27 and ∆x = -1

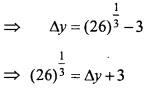
∆y is appromimately equal to dy

Approximate value of (26)1/3
= ∆y + 3
= 3 – 0.037 = 2.963
![]()
Question 31.
If the radius of the sphere is measured as 9cm with an error 0.03 cm then find the approximate error in calculating its surface area? (NCERT)
Solution:
Let the radius of circle = r
Given:
r = 9 cm, ∆r = 0.03 cm
Area of sphere

= (8πr) × 0.03
= 8π × 9 × 0.03 = 2.16 π cm2
The approximate error in caluculating the surface area is = 2.16 π cm2
Question 32.
If the radius of a sphere is measured as 7m with an error of 0.02m then find the approximate error in calculating its volume?
Solution:
Let the radius of sphere = r
and ∆r be the error in measuring the radius.
r = 7m, ∆r = 0.02 m (given)
Volume of sphere V = \(\frac{4}{3}\) πr3

The approximate error in calculating the volume is 3.92π m3
![]()
Question 33.
Find the approximate change in the volume V of a cube of sides x metre caused by increasing the side by 1%? (NCERT)
Solution:
Let x be the sides of cube.
Volume of cube V = x3, ∆x = 1% of x = \(\frac{x}{100}\)
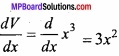
Change in volume ∆V = ( \(\frac { dV }{ dx } \) ) ∆x
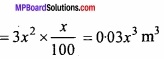
Approximate change in volume = 0.03 x3m3.
Question 34.
Find the approximate change in voume V of a cube of side x metre caused by increasing the side by 2%
Solution:
Let x be the side of cube,
∆x = 2% of x = \(\frac { x\times 2 }{ 100 } \) = 0.02 x
Volume of cube V = x3
\(\frac { dv }{ dx } \) = \(\frac { d }{ dx } \) x3 = 3x2
dV = ( \(\frac { dv }{ dx } \) ) ∆x = 3x2 × 0.02 x = 0.06x3 m3
Thus the approximate change in voume = 0.06 x3m3.