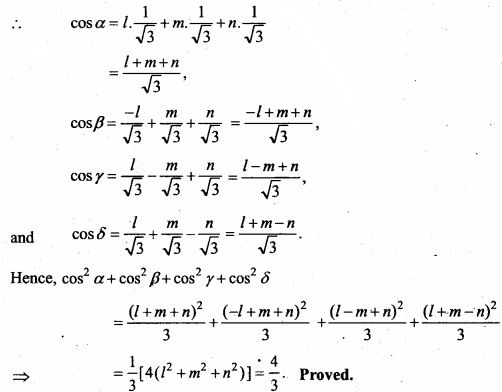MP Board Class 12th Maths Important Questions Chapter 11 Three Dimensional Geometry
Three Dimensional Geometry Important Questions
Three Dimensional Geometry Objective Type Questions
Question 1.
Choose the correct answer:
Question 1.
The FZ – plane divides the line segment joining the points P (- 2, 4, 7) and Q (3, -5, 8) in the ratio:
(a) 2 : 3
(b) 1 : 2
(c) 2 : 5
(d) 3 : 4
Answer:
(a) 2 : 3
Question 2.
If a line makes an angle \(\frac { \pi }{ 4 } \) with both the positive direction of the x – axis, and y – axis, then the angle made by the line with positive direction of the Z – axis is:
(a) \(\frac { \pi }{ 6 } \)
(b) \(\frac { \pi }{ 3 } \)
(c) \(\frac { \pi }{ 4 } \)
(d) \(\frac { \pi }{ 2 } \)
Answer:
(d) \(\frac { \pi }{ 2 } \)
![]()
Question 3.
Equation of the line passing through the points (2, 3, 4) and (1, -2, 3) are:
(a) \(\frac { x-2 }{ 1 } \) = \(\frac { y-2 }{ -5 } \) = \(\frac { z-4 }{ 1 } \)
(b) \(\frac { x-2 }{ -1 } \) = \(\frac { y-3 }{ -5 } \) = \(\frac { z-4 }{ -1 } \)
(c) \(\frac { x-2 }{ -1 } \) = \(\frac { y-3 }{ 5 } \) = \(\frac { z-4 }{ -1 } \)
(d) \(\frac { x-2 }{ -1 } \) = \(\frac { y-3 }{ -5 } \) = \(\frac { z-4 }{ 1 } \)
Answer:
(b) \(\frac { x-2 }{ -1 } \) = \(\frac { y-3 }{ -5 } \) = \(\frac { z-4 }{ -1 } \)
Question 4.
Angle between the planes x + 2y + z + 7 = 0 and 2x + y – z + 13 = 0 is:
(a) \(\frac { \pi }{ 2 } \)
(b) \(\frac { \pi }{ 3 } \)
(c) \(\frac { 3\pi }{ 2 } \)
(d) π
Answer:
(b) \(\frac { \pi }{ 3 } \)
Question 5.
Equation to the plane which cuts off intercepts 2, 3, -4 on the axis is:
(a) \(\frac{x}{2}\) + \(\frac{y}{3}\) – \(\frac{z}{4}\) = 0
(b) \(\frac{x}{2}\) + \(\frac{y}{3}\) – \(\frac{z}{4}\) = -1
(c) \(\frac{x}{2}\) + \(\frac{y}{3}\) – \(\frac{z}{4}\) = 1
(d) None of these.
Answer:
(c) \(\frac{x}{2}\) + \(\frac{y}{3}\) – \(\frac{z}{4}\) = 1
![]()
Question 2.
Fill in the blanks:
- Direction cosine of unit vector \(\frac { 1 }{ \sqrt { 14 } } \) ( \(\hat { i } \) + 2\(\hat { j } \) + 3\(\hat { k } \) ) are ………………………….
- Direction cosine of X – axis are ………………………….
- Angle between the diagonals of cube is ………………………….
- Angle between the straight lines \(\frac{x}{1}\) = \(\frac{y}{0}\) = \(\frac{z}{-1}\) and \(\frac{x}{3}\) = \(\frac{y}{4}\)
= \(\frac{z}{5}\) is …………………………. - If the lines \(\frac { x-2 }{ 3 } \) = \(\frac { y-3 }{ 4 } \) = \(\frac { z-4 }{ k } \) and \(\frac { x-2 }{ 3 } \) = \(\frac { y-3 }{ 4 } \) = \(\frac { z-4 }{ k } \) are coplaner, then k …………………………..
- If the line makes an angle α, β, γ with the coordinate axis respectively, then cos2α + cos2β + cos2 γ = ……………………………..
- Intercept cut by the plane 2x + y – z = 5 on axis is ……………………………..
Answer:
- True
- False
- True
- True
- False
- True
- False
![]()
Question 3.
Write True/False:
- The points A (1, 2, 3), B (4, 0,4) and C (-2, 4, 2) are collinear.
- The angle between lines whose direction ratios are (3,4, 5) and (4, -3, 5) is 30°.
- Angle between the lines 2x = 3y = —z and 6x = -y = -4z is 90°.
- Shortest distance between two intersecting lines always zero.
- Angle between the lines \(\frac { x+1 }{ 3 } \) = \(\frac { y+1 }{ 2 } \) = \(\frac { z+2 }{ 4 } \) and plane 2x + y – 3z + 5 = 0 is cos-1 (\(\frac { 4 }{ \sqrt { 406 } } \) )
- Straight line \(\frac { x-2 }{ 1 } \) = \(\frac { y+1 }{ -2 } \) = \(\frac { z-4 }{ 1 } \) is parllel to the plane x + 3y + 5z = 4
- Equation of plane parallel to the X – axis is ax + by + d = 0.
Answer:
- True
- False
- True
- True
- False
- True
- False.
Question 4.
Match the following:

Answer:
- (c)
- (d)
- (a)
- (b)
- (e)

Answer:
- (e)
- (c)
- (b)
- (f)
- (d)
![]()
Question 5.
Write the answer in one word/sentence:
- Find the direction ratios of the normal of the plane x + 2y + 3z + 4 = 0.
- Find the equation of the plane which intercepts unit length from the coordinate axis.
- Find the equation of the plane which is perpendicular on FOZ-plane.
- Find the angle between the planes x + 2y + z + 7 = 0 and 2x + y – z + 13 = 0.
- Find the distance between the parallel planes 2x – 2y + z + 3= 0 and 4x – 4y + 2z.
- Find the angle between the lines \(\frac{x}{2}\) = \(\frac{y}{-1}\) = \(\frac{z}{1}\) and \(\frac{x}{1}\) = \(\frac{y}{1}\) = \(\frac{z}{2}\)
- If a line makes α, β, γ with the positive direction of the axis, then find the value of sin2α +sin2 β + sin2γ.
Answer:
- (1, 2, 3)
- x + y + z = 1
- by + cz + d = 0
- \(\frac { \pi }{ 3 } \)
- \(\frac{1}{6}\)
- \(\frac { \pi }{ 3 } \)
- 2
Three Dimensional Geometry Short Answer Type Questions
Question 1.
Find the direction cosine of the line joining two points (-2, 4, -5) and (1, 2, 3)? (NCERT)
Answer:
Given points A (- 2, 4, – 5) and B (1, 2, 3).
Direction ratio of AB = 1 + 2, 2 – 4, 3 + 5
= 3, -2, 8

Direction cosine of AB

Question 2.
Find direction cosines of the line which makes an angle 90°, 135° and 45° with X, Y and Z axis respectively? (NCERT)
Solution:
Given α = 90°, β = 135°, λ = 45°
cos α = cos 90° = 0
cos β = cos 135° = cos (180° – 45°)
= – cos 45° = – \(\frac { 1 }{ \sqrt { 2 } } \)
cos λ = cos 45° = \(\frac { 1 }{ \sqrt { 2 } } \)
Direction cosines are cos α, cos β, cos λ
i.e; 0, – \(\frac { 1 }{ \sqrt { 2 } } \), \(\frac { 1 }{ \sqrt { 2 } } \)
Question 3.
A line OP, makes the angle 120° and 60° with X – axis and Y – axis respectively find the angle made by line with Z – axis?
Solution:
Given α = 120°, β = 60°.
Let the angle made by the line with Z – axis be γ then
cos2α + cos2β + cos2 γ = 1
⇒ cos2 120° + cos2 60° + cos2 γ = 1

Hence, the required angle is 45° or 135°.
Question 4.
Show that the points (2, 3, 4), (-1, -2, 1) and (5, 8, 7) are collinear? (NCERT)
Solution:
Given Points are A (2, 3, 4), B (-1,-2, 1), C (5, 8, 7)
Direction ratio of AB x2 – x1, y2 – y1, z2 – z1
= – 1 – 2, – 2 – 3, 1 – 4
= – 3, – 5, – 3 = – (3, 5, 3)
Direction ratio of BC x2 – x1, y2 – y1, z2 – z1
= 5 + 1, 8 + 2, 7 – 1
= 6, 10, 6 = 2 (3, 5, 3)
It is clear that direction ratio of AB and BC are proportional, hence AB is parallel to BC but point B is common to both AB and BC therefore A, B, C are collinear. Proved.
Question 5.
If direction cosine of a line are cos α, cos β and cos γ then prove that:
cos 2α + cos 2β + cos 2γ = – 1.
Solution:
L.H.S. = cos2α + cos2β + cos2γ
= 2cos2α – 1 + 2cos2β – 1 + 2cos2γ – 1
= 2 (cos2α + cos2β + cos2γ) – 3
= 2 × 1 – 3, [∵ cos2α + 2β + cos2γ – 1]
= -1
= R.H.S. Proved.
![]()
Question 6.
Prove that the line passing through the points (1, -1, 2) and (3, 4, -2) are perpendicular to the lines passing through the points (0, 3, 2) and (3, 5, 6). (NCERT)
Solution:
Direction ratio’s of the line joining points (1, -1, 2) and (3, 4, -2)
= 3 – 1, 4 + 1, – 2 – 2
= 2, 5, – 4 = a1, b1, c1 (let)
Direction ratios’s of the line joining the points (0, 3, 2) and (3, 5, 6)
= 3 – 0, 5 – 3, 6 – 2
= 3,2,4
= a2, b2, c2 (let)
Lines will be perpendicular if
a1a2 + b1b2 + c1c2 = 0
⇒ 2.3 + 5.2 – 4.4 = 0
⇒ 16 – 16 = 0
⇒ 0 = 0. Proved.
Question 7.
Prove that the line joining the points A (1, 2, 3) and B (2, 3, 5) are parallel to then line joining the points C (-1, 2, -3) and D ( 1, 4, 1)?
Solution:
Direction ratio of line AB
= 2 – 1, 3 – 2, 5 – 3
= 1, 1, 2
= a1, b1, C1
Direction ratio of line CD
= 1 + 1, 4 – 2, 1 + 3
= 2, 2, 4
= a2, b2, c2
Where \(\frac { a_{ 1 } }{ a_{ 2 } } \) = \(\frac { b_{ 1 } }{ b_{ 2 } } \) = \(\frac { c_{ 1 } }{ c_{ 2 } } \)
= \(\frac{1}{2}\) = \(\frac{1}{2}\) = \(\frac{2}{4}\) or \(\frac{1}{2}\)
Hence line AB and CD are parallel. Proved.
![]()
Question 8.
Find the angle between the lines \(\frac{x}{2}\) = \(\frac{y}{2}\) = \(\frac{z}{1}\) and \(\frac{x – 5}{4}\) = \(\frac{y – 2}{1}\) = \(\frac{z – 3}{8}\)? (NCERT)
Solution:
Equation of the lines are
\(\frac{x}{2}\) = \(\frac{y}{2}\) = \(\frac{z}{1}\)
and \(\frac{x – 5}{4}\) = \(\frac{y – 2}{1}\) = \(\frac{z – 3}{8}\)
a1 = 2, b1 = 2, c1 = 1
a2 = 4, b2 = 1, c2 = 8
Let the angle between them = θ
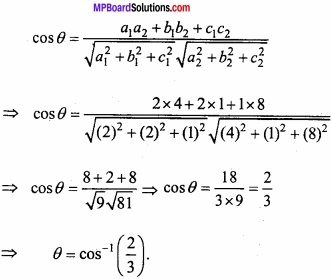
Question 9.
Prove that lines
\(\frac{x – 5}{7}\) = \(\frac{y + 2}{- 5}\) = \(\frac{z}{1}\) and \(\frac{x}{1}\) = \(\frac{y}{2}\) = \(\frac{z}{3}\) are perpendicular? (NCERT)
Solution:
\(\frac{x – 5}{7}\) = \(\frac{y + 2}{- 5}\) = \(\frac{z}{1}\)
and \(\frac{x}{1}\) = \(\frac{y}{2}\) = \(\frac{z}{3}\)
Where a1 = 7, b1 = -5, c1 = 1
a2 = 1, b2 = 2, c2 = 3
a1a2 + b1b2 + c1c2 = 7(1) + (- 5)(2) + 1 × 3
= 10 -10 = 0
Hence, the lines are perpendicular. Proved.
![]()
Question 10.
Find the cartesion equation of the line which passes through the point (-2, 4, -5) and parallel to the line given by \(\frac { x+3 }{ 3 } \) = \(\frac { y-4 }{ 5 } \) = \(\frac { z+8 }{ 8 } \). (NCERT)
Solution:
Equation of given line
\(\frac { x+3 }{ 3 } \) = \(\frac { y-4 }{ 5 } \) = \(\frac { z+8 }{ 8 } \) ………. (1)
Direction ratio of (1) is 3, 5, 8
Equation of line passing through point (- 2, 4, -5)
\(\frac { x+2 }{ a } \) = \(\frac { y-4 }{ b } \) = \(\frac { z+5 }{ c } \) ……………….. (2)
Direction ratio of eqn. (2) is a, b, c
Eqns. (1) and (2) are parallel
∴\(\frac{a}{3}\) = \(\frac{b}{5}\) = \(\frac{c}{8}\) = k
a = 3k, b = 5k, c = 8k
Putting the value of a, b, c in eqn. (2) we get
\(\frac { x+2 }{ 3k } \) = \(\frac { y-4 }{ 5k } \) = \(\frac { z+5 }{ 8k } \)
\(\frac { x+2 }{ 3 } \) = \(\frac { y-4 }{ 5 } \) = \(\frac { z+5 }{ 8 } \).
Question 11.
Find the eqution of straight line passing through point (1, 2, 3) are parallel to \(\frac{x-6}{12}\) = \(\frac{y-2}{4}\) = \(\frac{z+7}{5}\)?
Solution:
Equation of line passing through point (x1, y1, z1) and direction ratio a, b, c is
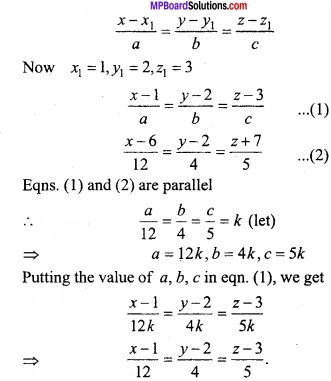
Question 12.
Find the angle between the lines \(\frac{x}{1}\) = \(\frac{y}{0}\) = \(\frac{z}{3}\) and \(\frac{x}{4}\) = \(\frac{y}{5}\) = \(\frac{z}{0}\)?
Solution:
Equation of given lines
\(\frac{x}{1}\) = \(\frac{y}{0}\) = \(\frac{z}{3}\) …………………. (1)
and \(\frac{x}{4}\) = \(\frac{y}{5}\) = \(\frac{z}{0}\) ……………………… (2)
Where a1 = 1, b1 = 0, c1 = 3 and a2 = 4, b2 = 5, c2 = 0
Let θ be the angle between eqns. (1) and (2)

Question 13.
Find the condition that the lines x = ay + b, z = cy + d and x = a’y + b’, z = c’y + d’ are perpendicular?
Solution:
x = ay + b and z = cy + 4
⇒ \(\frac { x-b }{ a } \) = \(\frac { y }{ 1 } \) and \(\frac { z-d }{ c } \) = \(\frac { y }{ 1 } \)
Hence the corresponding equation
\(\frac { x-b }{ a } \) = \(\frac { y }{ 1 } \) = \(\frac { z-d }{ c } \) ………………….. (1)
Again x = a’y + b’ and z = c’y + d’ equation is
\(\frac { x-b^{ ‘ } }{ a^{ ‘ } } \) = \(\frac { y }{ 1 } \) = \(\frac { z-d^{ ‘ } }{ c^{ ‘ } } \) ………………… (2)
Eqns. (1) and (2) are perpendicular.
a × a’ + 1 × 1 + c × c’ = 0
⇒ aa’ + cc’ + 1 = 0 is the required condition.
![]()
Question 14.
(A) Find the angle between the lines \(\vec { r } \) = ( \(\hat { i } \) + 3\(\hat { j } \) + 5\(\hat { k } \) ) + t ( \(\hat { i } \) – 2\(\hat { j } \) – 3\(\hat { k } \) ) and \(\vec { r } \) = ( \(\hat { i } \) – 2\(\hat { j } \) + 5\(\hat { k } \) ) + s(2\(\hat { i } \) – 2\(\hat { j } \) + \(\hat { k } \) )?
Solution:

(B) Find the angle between lines \(\vec { r } \) = (3\(\hat { i } \) + 4\(\hat { j } \) – 2\(\hat { k } \) ) + t(-\(\hat { i } \) + 2\(\hat { j } \) + \(\hat { k } \) ) and \(\vec { r } \) = ( \(\hat { i } \) – 7\(\hat { j } \) – 2\(\hat { k } \) ) + s( \(\hat { i } \) + 3\(\hat { j } \) + 2\(\hat { k } \) )
Solution:
Solve like Q. 14. (A)
Question 15.
Find angle between two planes 2x – y + z = 6 and x + y + 2z = 7?
Solution:
Given planes are:
2x – y + z = 6 ……………. (1)
and x + y + 2z = 7 ………………… (2)
Direction ratio of eqn. (1) = 2, -1, 1 1 ⇒ A1, B1, C1
Direction ratio of eqn. (2) = 1, 1, 2 ⇒ A2, B2, C2
Let θ be the angle between them
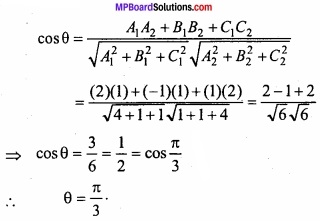
Question 16.
(A) If plane 3x – 6y – 2z = 7 and 2x + y – kz = 5 are perpendicular to each other. Find the value of k?
Solution:
Equation of given planes are
3x – 6y – 2z = 7 ………………………… (1)
and 2x + y – kz = 5 …………………… (2)
Where a1 = 3, b1 = -6, c1 = -2, and a2 = 2, b2 = 1, c2 = -k
Planes (1) and (2) are perpendicular
∴ a1a2 + b1b2 + c1c2 = 0
⇒ (3) (2) + (-6) (1) + (-2) (-k) = 0
⇒ 6 – 6 + 2k = 0
⇒ 2k = 0
⇒ k = 0.
![]()
(B) For which value of k the planes 2x + ky + z + 9 = 0 and 5x + 3y – 4z – 6 = 0 are perpendicular?
Solution:
Solve like Q.16 (A)
[Answer: k = -2]
(C) Prove that the planes x + 2y + 3z = 6 and 5x – 3y + z = 1 are perpendicular?
Solution:
Given equation of planes are:
x + 2y + 3z = 6 ……………………. (1)
and 3x – 3y + z = 1 ……………………… (2)
Direction ratio of eqn. (1) = 1, 2, 3
Direction ratio of eqn. (2) = 3,- 3, 1
∴ a1a2 + b1b2 + c1c2 = (1)(3) + 2(-3) + (3)(1)
= 3 – 6 + 3 = 0
Hence planes (1) and (2) are perpendicular. Proved.
Question 17.
A plane meets the co – ordinate axes at points A, B and C. If the centroid of ∆ABC is (2, – 1, 3) then find the equation of the plane?
Solution:
Let A(a, 0, 0), B(0, b, 0), C(0, 0, c)
∵ OA = a, OB = b, OC = c
Centroid (given) is (2,- 1, 3)

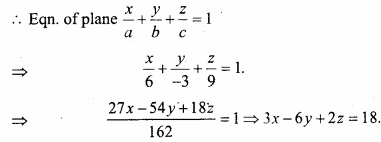
Question 18.
A plane meets the coordinate axes in A, B, C such that the centroid of ∆ABC is (a, b, c). Find the equation of the plane is \(\frac{x}{a}\) + \(\frac{y}{b}\) + \(\frac{z}{c}\) = 3?
Solution:

Question 19.
Find the equation of plane which is parallel to the plane 2x + 3y – z = 8 and passes through the point (1, 2, 3)?
Solution:
Any plane parallel to the plane
2x + 3y – z = 8
⇒ 2x + 3y – z + λ = 0 ………………….. (1)
∵ It passes through the point (1,2, 3), then
2(1) + 3(2) – 3 + λ = 0
⇒ 2 + 6 – 3 + λ = 0
⇒ 8 – 3 + λ = 0
⇒ 5 + λ = 0
⇒ λ = -5 ……………………… (2)
∴ From eqns. (1) and (2), we have
2x + 3y – 5 = 0.
![]()
Question 20.
Find the direction cosines of normal to the plane 2x + 4y + 4z = 9?
Solution:
Equation of given plane is:
2x + 4y + 4z = 9 …………………… (1)
The direction ratios of normal to the given plane are 2, 4, 4
Hence the direction cosines of the normal are

Question 21.
Find the equation of plane on which the length of perpendicular drawn from origin is 5 unit and the direction cosines of normal to it are \(\frac { 1 }{ \sqrt { 3 } } \), \(\frac { 1 }{ \sqrt { 3 } } \), – \(\frac { 1 }{ \sqrt { 3 } } \)?
Solution:
Equation of plane in normal form
lx + my + nz = p
Given: l = \(\frac { 1 }{ \sqrt { 3 } } \), m = \(\frac { 1 }{ \sqrt { 3 } } \), n = – \(\frac { 1 }{ \sqrt { 3 } } \), p = 5
Putting in eqn. (1),
\(\frac { 1 }{ \sqrt { 3 } } \) x + \(\frac { 1 }{ \sqrt { 3 } } \) y – \(\frac { 1 }{ \sqrt { 3 } } \) z = 5
⇒ x + y – z = 5\(\sqrt{3}\)
Question 22.
Find the equation of plane on which length of perpendicular drawn from origin is 4 units and whose direction cosines are in proportional to 2, -3, 6?
Solution:
Let the equation of plane
lx + my + nz = p
Given:
p = 4, a = 2, b = -3, c = 6

Putting in eqn. (1),
\(\frac{2}{7}\) x – \(\frac{3}{7}\) y + \(\frac{6}{7}\) z = 4
⇒ 2x – 3y + 6z = 28.
Question 23.
Find the equation of plane on which length of perpendicular drawn from origin is 5 unit and the direction ratios of normal to the plane are 2, 3, 6.
Solution:
Solve as Q. No. 22.
[Answer: 2x + 3y + 6z = 35]
![]()
Question 24.
Find the equation of the plane which passes through the point (1, – 2, 3) and perpendicular to line whose direction ratios are 2, 1, -1?
Solution:
We know that equation of the plane passing through a point (x1, y1, z1) is
a (x – x1) + b( y – y1) + c (z – z1) = 0
Where, a, b and c are the direction ratios of normal to the plane
Here the point (x1, y1, z1) is (1, -2, 3)
and the direction ratios a, b, c are 2, 1, -1. Therefore by eqn. (1) we get
2. (x – 1) + 1. ( y + 2) -1. (z – 3) = 0
⇒ 2x + y – z – 2 + 2 + 3 = 0
⇒ 2x + y – z + 3 = 0
Which is the required equation of the plane.
Question 25.
(A) Find the perpendicular distance of the plane 6x – 3y + 2z – 14 = 0 from origin?
Solution:
Equation of plane,
6x – 3y + 2z – 14 = 0
The length of perpendicular drawn from (0, 0, 0) to the plane

(B) Find the length of perpendicular drawn from (1, 2, 0) on the plane 4x + 3y + 12z + 16 = 0?
Solution:
Equation of plane,
4x + 3y + 12z + 16 = 0
The length of perpendicular drawn from (1, 2, 0) to the plane
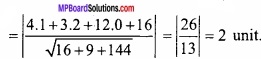
(C) Find the length of perpendicular drawn from (7, 14, 5) to the plane 2x + 4y – z?
Solution:
Solve as Q.No. 25 (B)
Answer:
3\(\sqrt{21}\) unit.
Question 26.
Find the equation of plane which passes through the point (- 1, 2, 3) and parallel to the plane 3x + 4y – 5z = 52?
Solution:
The given plane is
3x + 4y – 5z = 52 …………………… (1)
A plane parallel to the given plane (1),
3x + 4y – 5z = λ ………………(2)
∵ Plane (2) passes through the point (-1, 2, 3)
∴ 3(-1) + 4(2) – 5(3) = λ
⇒ -3 + 8 – 15 = λ
⇒ -18 – 8 = λ
⇒ -10 = λ
∴ From eqn. (2), putting the value of λ
3x + 4y – 5z = -10
∴ The required plane is
3x + 4y – 5z + 10 = 0
![]()
Question 27.
(A) Find the intercepts made by the plane 3x + 4y – 7z = 84 from the co – ordinate axes?
Solution:

(B) Find the intercepts made by the plane 3x + 4y – 6z = 72 from the co – ordinate axes?
Solution:
Solve as Q. No. 27 (A).
[Answer: (24, 18, -12).]
Question 28.
Find the equation of plane parallel to the X – axis and cuts intercepts 5 and 7 from Y and Z – axis respectively?
Solution:
Let the equation of plane
\(\frac{x}{a}\) + \(\frac{y}{b}\) + \(\frac{z}{c}\) = 1
The plane (1) is parallel to X – axis
a = ∞
Given b = 5, c = 7
∴ \(\frac{x}{∞}\) + \(\frac{y}{5}\) + \(\frac{z}{7}\) = 1
⇒ \(\frac{y}{5}\) + \(\frac{z}{7}\) = 1 [∵\(\frac{x}{∞}\) = 0]
⇒ 7y + 5z = 35.
Question 29.
Find the equation of the plane passing through the points (0, 0, 0) and perpendicular to the planes x + 2y – z = 1 and 3x – 4y + z = – 5?
Solution:
Equation of the plane passing through point (0,0,0)
a(x – 0) + b(y – 0) + c(z – 0) = 0
⇒ ax + by + cz = 0 ………………………… (1)
Plane (1) is perpendicular to the given planes.
x + 2y – z = 1 and 3x – 4y + z = -5
a + 2b – c = 0 ………………….. (2)
3a – 4b + c = 0 ………………………….. (3)
Solving eqns. (2) and (3),
\(\frac { a }{ 2-4 } \) = \(\frac { -b }{ 1+3 } \) = \(\frac { c }{ -4-6 } \)
⇒ \(\frac { a }{ -2 } \) = \(\frac { -b }{ 4 } \) = \(\frac { c }{ -10 } \)
⇒ \(\frac{a}{1}\) = \(\frac{b}{2}\) = \(\frac{c}{5}\) = k (say)
∴ a = k, b = 2k and c = 5k, where k ≠ 0.
∴ From eqn. (1),
k [x + 2y + 5z] = 0
∴ x + 2y + 5z = 0.
![]()
Question 30.
Find the equation of the plane parallel to X – axis and passes through the points (2, 3, -4) and (1, -1, 3)?
Solution:
Let the equation of the plane parallel to X – axis is
by + cz + d= 0 ………………………. (1)
It passes through the points (2, 3, – 4) and (1, -1, 3), then
3b – 4c + d = 0 ……………………….. (2)
and – b + 3c + d = o …………………….. (3)
Solving eqns. (2) and (3), we get
\(\frac { b }{ -4-3 } \) = \(\frac { c }{ -1-3 } \) = \(\frac { d }{ 9-4 } \)
⇒ \(\frac{b}{7}\) = \(\frac{c}{4}\) = \(\frac{d}{-5}\) = k (say)
∴ b = 7k, c = 4k, d = -5k
Put the values of b, c and d in eqn. (1), we get
7ky + 4kz – 5k = 0
⇒ 7y + 4z – 5 = 0
This is the required equation of the plane.
Question 31.
Prove that the distance between two parallel planes 2x – 2y + z + 3 = 0 and 4x – 4y + 2z + 5 = 0 is \(\frac{1}{6}\)?
Solution:
The equations of the plane are 4x – 4y + 2z + 5 = 0
2x – 2y + z + 3 = 0 ……………… (1)
and 4x – 4y + 2z + 5 = 0 ………….. (2)
The length of the perpendicular drawn from O (0, 0, 0) to the plane (1) is

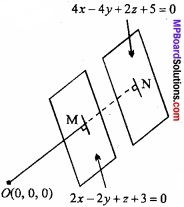
and the length of the perpendicular drawn from O (0, 0, 0) to the plane (2) is

∴ The required distance MN = P1 – P2
= 1 – \(\frac{5}{6}\) = \(\frac{6-5}{6}\) = \(\frac{1}{6}\). Proved.
Question 32.
(A) Find the equation of the plane passes through the intersecting line of the planes x + y + z – 6 = 0 and 2x + 3y + 4z + 5 = 0 and also through the point (1, 1, 1)?
Solution:
The given planes are
x + y + z – 6 = 0 …………………. (1)
and 2x + 3y + 4z + 5 = 0 ………………….. (2)
The equation of the plane passes through the intersecting line of the planes (1) and (2), is
(x – y + z – 6) + λ (2x + 3y + 4z + 5) = 0 ………………….. (3)
Because plane (3) passes through the point (1, 1, 1), then
(1 + 1 + 1 – 6) + (2 + 3 + 4 + 5) = 0
⇒ – 3 + λ (14) = 0
⇒ λ = \(\frac{3}{14}\)
Putting the value of λ in eqn.(3),
(x + y + z – 6) + \(\frac{3}{14}\) (2x + 3y + 4z + 5) = 0
⇒ 20x + 23y + 26z – 69 = 0.
(B) Find the equation of the plane passing through the intersecting line of the planes x + 2y + 3z = 5 and 2x – 4y + z = 3 and also through the point (0, 1, 0)?
Solution:
Solve as Q.No. 32. (A).
[Answer: 3x – 2y + 4z + 2 = 0.]
![]()
Question 33.
(A) Find the vector equation of a plane passing through the point 2\(\hat { i } \) – \(\hat { j } \) + \(\hat { k } \) and perpendicular to the vector 6\(\hat { i } \) + 2\(\hat { j } \) – 3\(\hat { k } \)?
Solution:
Let the equation of plane be
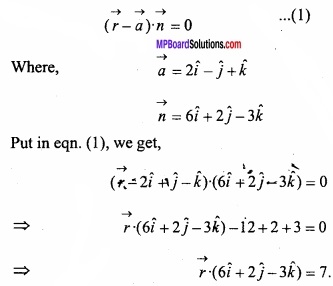
(B) Find the vector equation of the plane which is at a distance 7 units from origin and perpendicular to the vector 4\(\hat { i } \) + 2\(\hat { j } \) – 3\(\hat { k } \)?
Solution:
Let the equation of plane be

(C) Find the distance of the point (2, – 1, 3) from the plane \(\vec { r } \). (3\(\hat { i } \) + 2\(\hat { j } \) – 6\(\hat { k } \) ) + 15 = 0?
Solution:

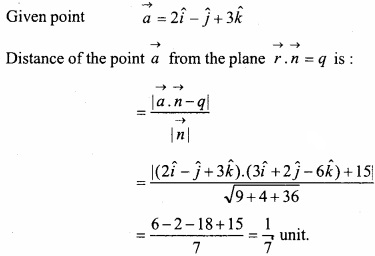
(D) Find the distance from the point (2\(\hat { i } \) – \(\hat { j } \) – 4\(\hat { k } \) ) to the plane \(\vec { r } \). (3\(\hat { i } \) – 4\(\hat { j } \) + 12\(\hat { k } \) ) = 19?
Solution:

Question 34.
Find the angle between the planes \(\vec { r } \). (2\(\hat { i } \) – 3\(\hat { j } \) + 4\(\hat { k } \) ) = 1 and \(\vec { r } \) (- \(\hat { i } \) + \(\hat { j } \) ) = 4?
Solution:

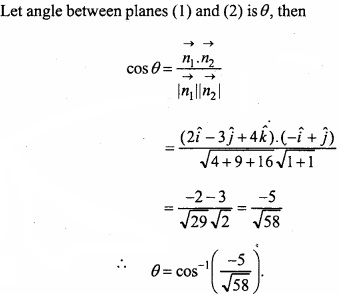
Three Dimensional Geometry Long Answer Type Questions – I
Question 1.
Find the perpendicular distance of line \(\frac{x}{1}\) = \(\frac{y-1}{2}\) = \(\frac{z-2}{3}\) from the point (1, 6, 3)?
Solution:
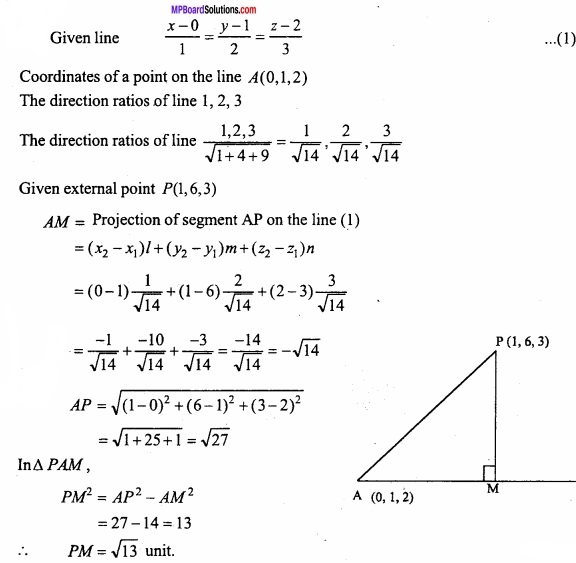
Question 2.
Find the distance between two parallel lines \(\frac { x-1 }{ 2 } \) = \(\frac { y-2 }{ 3 } \) = \(\frac { z-3 }{ 4 } \) and \(\frac { x-2 }{ 4 } \) = \(\frac { y-3 }{ 6 } \) = \(\frac { z-4 }{ 8 } \)?
Solution:
Given lines:
\(\frac { x-1 }{ 2 } \) = \(\frac { y-2 }{ 3 } \) = \(\frac { z-3 }{ 4 } \) …………………… (1)
and \(\frac { x-2 }{ 4 } \) = \(\frac { y-3 }{ 6 } \) = \(\frac { z-4 }{ 8 } \) ………………………… (2)
Any point P (1, 2, 3) lies on line (1). Now we find the length of perpendicular PM drawn from point P (1, 2, 3) to eqn. (2).
∵Eqn. (2) passes through point A (2, 3,4)

![]()
Question 3.
Find the equation plane passing through the line \(\frac { x-3 }{ 2 } \) = \(\frac { y+2 }{ 3 } \) = \(\frac { z-4 }{ -1 } \) and point (-6, 3, 2)?
Solution:
Let the equation of plane be
A(x – α) + B(y – β) + C(z – γ) = 0
Passes through line \(\frac { x-3 }{ 2 } \) = \(\frac { y+2 }{ 3 } \) = \(\frac { z-4 }{ -1 } \)
∴ A(x – 3) + B(y + 2) + C(z – 4) = 0 ………………………… (1)
Plane passes through point (-6, 3, 2)
∴ A(-6 – 3) + B(3 + 2) + C(2 – 4) = 0
⇒ -9A + 5B – 2C = 0
⇒ 9A – 5B + 2C = 0 …………………………… (2)
Direction ratio of plane →A, B, C
2A + 3B – C = 0
Solving eqns. (2) and (3)
9A – 5B + 2C = 0
2A + 3B – C = 0
\(\frac { A }{ 5-6 } \) = \(\frac { B }{ 4+9 } \) = \(\frac { C }{ 27+10 } \)
⇒ \(\frac { A }{ -1 } \) = \(\frac { B }{ 13 } \) = \(\frac { C }{ 37 } \)
Putting in eqn. (1)
-1(x – 3) + 13(y + 2) + 37(z – 4) = 0
⇒ -x + 3 + 13y + 26 + 37z – 148 = 0
⇒ -x + 13y + 37z – 119 = 0
⇒ x – 13y – 37z + 119 = 0.
![]()
Question 4.
Find the shortest distance between the straight lines \(\frac { x-3 }{ 3 } \) = \(\frac { y-8 }{ -1 } \) = \(\frac { z-3 }{ 1 } \) and \(\frac { x
+3 }{ -3 } \) = \(\frac { y+7 }{ 2 } \) = \(\frac { z-6 }{ 4 } \)?
Solution:
Here, x1 = 3, y1 = 8, z1 = 3, x2 = -3, y2 = -7, z2 = 6
a1 = 3, b1 = -1, c1 = 1, a2 = -3, b2 = 2, c2 = 4
Given lines are
\(\frac { x-3 }{ 3 } \) = \(\frac { y-8 }{ -1 } \) = \(\frac { z-3 }{ 1 } \) and \(\frac { x+3 }{ -3 } \) = \(\frac { y+7 }{ 2 } \) = \(\frac { z-6 }{ 4 } \)
We know that the shortest distance between 2 lines \(\frac { x-x_{ 1 } }{ a_{ 1 } } \) = \(\frac { y-y_{ 1 } }{ b_{ 1 } } \) = \(\frac { z-z_{ 1 } }{ c_{ 1 } } \) and \(\frac { x-x_{ 2 } }{ a_{ 2 } } \) = \(\frac { y-y_{ 2 } }{ b_{ 2 } } \) = \(\frac { z-z_{ 2 } }{ c_{ 2 } } \) is

Question 5.
Find the coordinates of point of intersection of the lines \(\frac { x-1 }{ 2 } \) = \(\frac { y-2 }{ 3 } \) = \(\frac { z-3 }{ 4 } \) and \(\frac { x-2 }{ 3 } \) = \(\frac { y-3 }{ 4 } \) = \(\frac { z-4 }{ 5 } \)?
Solution:
Let \(\frac { x-1 }{ 2 } \) = \(\frac { y-2 }{ 3 } \) = \(\frac { z-3 }{ 4 } \) = r
∴ x = 2r + 1, y = 3r + 2, z = 4r + 3
Suppose the above point is intersection point then it will satisfy line

Put in eqn.(1), we get
x = 2(-1) + 1, y = 3(-1) + 2, z = 4(-1) + 3
x = -1, y = -1, z = -1
∴ Intersection point (-1, -1, -1).
Question 6.
Find the coordinates of point of intersection of the lines x – 3 = \(\frac { y+4 }{ -3 } \) = \(\frac { z-5 }{ 3 } \) and x – 4 = \(\frac { y-5 }{ 3 } \) = \(\frac { z+6 }{ -4 } \)?
Solution:
Given lines are \(\frac { x-3 }{ 1 } \) = \(\frac { y+4 }{ -3 } \) = \(\frac { z-5 }{ 3 } \) ……………….. (1)
and \(\frac { x-4 }{ 1 } \) = \(\frac { y-5 }{ 3 } \) = \(\frac { z+6 }{ -4 } \) ……………………… (2)
x1 = 3, y1 = -4, z1 = 5, l1 = 1, m1 = -3, n1 = 3
x2 = 4, y2 = 5, z2 = -6, l2 = 1, m2 = 3, n2 = -4
If lines (1) and (2) are intersect, then

⇒ 1(12 – 9) -1(-36 + 33) + 1(27 – 33) = 0
⇒ 3 + 3 – 6 = 0
⇒ 0 = 0
Hence the lines (1) and (2) are intersect
Again let \(\frac { x-3 }{ 1 } \) = \(\frac { y+4 }{ 3 } \) = \(\frac { z-5 }{ 3 } \) = r
∴ x = r + 3, y = -3r – 4, z = 3r + 5 ……………………………… (3)
Suppose above point is point of intersection hence it will satisfy eqn. (2)

Putting r = -1 in eqn. (3),
We get x = -1 + 3, y = -3(-1) – 4, z = 3(-1) + 5
x = 2, y = -1, z = 2
∴Intersection point (2, -1, 2).
Question 7.
Find the shortest distance between the lines:
\(\vec { r } \) = \(\hat { i } \) + 2\(\hat { j} \) + 3\(\hat { k } \) + t(2\(\hat { i } \) + 3\(\hat { j } \) + 4\(\hat { k } \) ) and \(\vec { r } \) = 2\(\hat { i } \) + 4\(\hat { j } \) + 5\(\hat { k } \) + s(3\(\hat { i } \) + 4\(\hat { j } \) + 5\(\hat { k } \) )?
Solution:
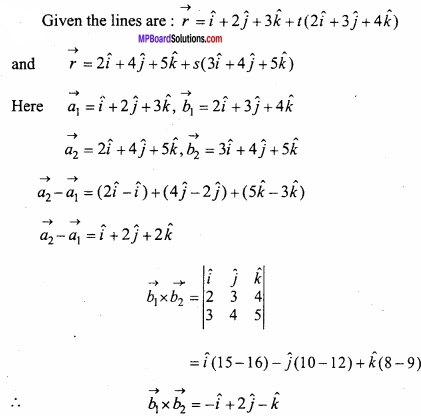

Question 8.
Prove that the lines \(\vec { r } \) = ( \(\hat { i } \) + \(\hat { j } \) – \(\hat { k } \) ) + λ(3\(\hat { i } \) r =(3\(\hat { i } \) – \(\hat { j } \) ) and \(\vec { r } \) = (4\(\hat { i } \) – \(\hat { k } \) ) + μ (2\(\hat { i } \) + 3\(\hat { k } \) are intersect to each other. Also And the point of intersection?
Solution:
Given lines are
Equating the above lines (1) and (2)
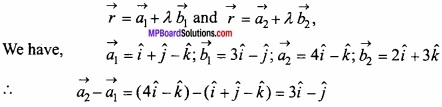
and two lines intersect each other, if


1 + 3λ = 4 + 2μ …………….. (3)
1 – λ = 0 ………………….. (4)
and -1 = 3μ – 1 ………………… (5)
From eqn. (4) we get
1 – λ = 0 ⇒ λ = 1
From eqn.(5) we get λ and μ in eqns. (1) and (2) respectively, we get
μ = 0
The above values of

Question 9.
(A) Find the shortest distance between the lines:
\(\vec { r } \) = (3 – t) \(\hat { i } \) + (4 + 2t) \(\hat { j } \) + (t – 2) \(\hat { k } \)
and \(\vec { r } \) = (1 + s) \(\hat { i } \) + (3s – 7) \(\hat { j } \) + (2s – 2) \(\hat { k } \)?
Solution:
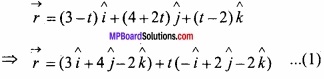

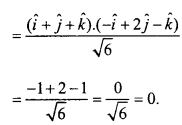
(B) Find the shortest distance between the lines:
\(\vec { r } \) = (λ – 1) \(\hat { i } \) + (λ + 1) \(\hat { j } \) + (1 + λ) \(\hat { k } \)
\(\vec { r } \) = (1 – µ) \(\hat { i } \) + (2µ – 1) \(\hat { j } \) + (µ + 2) \(\hat { k } \)?
Solution:
Solve as Q.No. 9(A)
[Answer: S.D. = \(\frac { 5 }{ \sqrt { 2 } } \) ]
(C) Find the shortest distance between the lines whose vector equations are
\(\vec { r } \) = (1 + 2λ) \(\hat { i } \) + (2 + 3λ) \(\hat { j } \) + (3 + 4λ) \(\hat { k } \)
\(\vec { r } \) = (2 + 3µ) \(\hat { i } \) + (3 + 4µ) \(\hat { j } \) + (4 + 5µ) \(\hat { k } \)?
Solution:
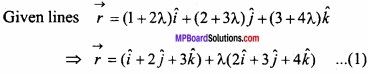
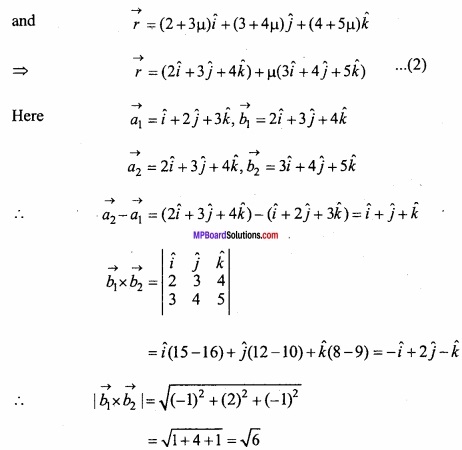
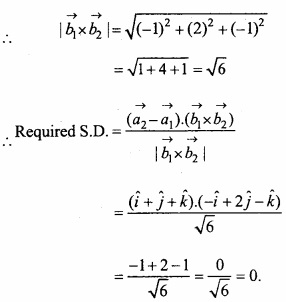
Question 10.
Find the equation of plane passing through the line of intersection of the planes x + 3y + 4z – 5 = 0 and 3x – 4y + 9z – 10 = 0 and perpendicular to the plane x + 2y = 0?
Solution:
Given equation of planes are
x + 3y + 4z – 5 = 0 ………………….. (1)
and 3x – 4y + 9z – 10 = 0 ………………………. (2)
The plane passing through the line of intersection of the planes (1) and (2)
(x + 3y + 4z – 5) + λ(3x – 4y + 9z – 10) = 0
⇒ (1 + 3λ) x + (3 – 4λ) y + (4 + 9λ) z – 5 – 10λ = 0 ………………… (3)
Again, given plane is
x + 2y = 0 ……………………… (4)
Plane (3) is perpendicular to the plane (4)
(1 + 3λ).1 + (3 – 4λ).2 + (4 + 9λ). 0 = 0
⇒ 1 + 3λ + 6 – 8λ = 0
⇒ λ = \(\frac{7}{5}\)
Putting the value of X in eqn. (3),
(x + 3y + 4z – 5) + \(\frac{7}{5}\) (3x – 4y + 9z – 10) = 0
⇒ 26x – 13y + 83z = 95.
![]()
Question 11.
Find the equation of planes which are parallel to the plane x – 2y + 2z = 3 and whose perpendicular distance from the point (1, 2, 3) is 1?
Solution:
The planes parallel to the given plane x – 2y + 2z = 3 is
x – 2y + 2z + λ = 0 ………………….. (1)
Perpendicular distance from the point (1, 2, 3) to the above plane is

Then substitute the value of 2 in eqn. (1), we have
x – 2y + 2z = 0, x – 2y + 2z = 6
Question 12.
(A) Find the equation of the plane passing through the points (1,-2, 4) and (3, -4, 5) and perpendicular to the plane x + y – 2z = 6?
Solution:
Equation of the plane passing through the point (1, -2, 4) is
A(x – 1) + B(y + 2) + C(z – 4) = 0 ………………………. (1)
It also passes through the point (3, -4, 5)
A(3 – 1) + 5(-4 + 2) + C(5 – 4) = 0
⇒ 2A – 2B + C = 0 …………………………. (2)
The given equation of plane is
x + y – 2z = 6 ……………………. (3)
The planes (1) and (3) are perpendicular
A + B – 2C = 0 ……………………. (4)
On solving by cross multiplication method, we get
\(\frac { A }{ 4-1 } \) = \(\frac { B }{ 1+4 } \) = \(\frac { C }{ 2+2 } \)
⇒ \(\frac{A}{3}\) = \(\frac{B}{5}\) = \(\frac{C}{4}\) = k
∴ A = 3k, B = 5k, C = 4k
Putting these values of A, B and C in eqn. (1), we get
⇒ 3k(x – 1) + 5k(y + 2) + 4k(z – 4) = 0
⇒ 3x – 3 + 5y + 10 + 4z – 16 = 0
⇒ 3x + 5y + 4z – 9 = 0.
(B) Find the equation of plane passing through the points (1, 1,-1) and (1, 1,-1) and perpendicular to the planes x + 2y + 2z = 9?
Solution:
Solve as Q.No. 12.(A)
[Answer: 2x + 2y – 3z + 3 = 0]
![]()
Question 13.
(A) Find the equation of plane passing through (1, 1, -1) and perpendicular to the planes x + 2y + 3z = 0 and 2x – 3y + 4z = 0?
Solution:
Let the equation of planes
A(x – x1) + B(y – y1) + C(z – z1) = 0
It passes through (1, 1, -1)
A(x – 1) + B(y – 1) + C(z + 1) = 0 …………………. (1)
Given planes are
x + 2y + 3z = 0 …………………… (2)
2x – 3y + 4z = 0 ………………………. (3)
The plane (1) is perpendicular to eqns. (2) and (3),
∴ 1A + 2B + 3C = 0
and 2A – 3B + 4C = 0
Solving \(\frac { A }{ 8+9 } \) = \(\frac { B }{ 6-4 } \) = \(\frac { C }{ -3-4 } \)
⇒ \(\frac{A}{17}\) = \(\frac{B}{2}\) = \(\frac{C}{-7}\) = k
∴ A = 17k, B = 2k, C = -7k
By eqn. (1),
17k (x – 1) + 2k (y – 1) – 7k (z + 1) = 0
⇒ 17x + 2y – 7z – 26 = 0.
(B) Find the equation of plane passing through (2, 1, 4) and perpendicular to the planes 9x – 7y + 6z + 48 = 0 and x + y – z = 0?
Solution:
Solve as Q.No. 13 (A)
[Answer: x + 15y + 16z = 81]
Question 14.
Find the equation of the plane passing through the points (2, 2, -1), (3, 4, 2) and (7, 0, 6)?
Solution:
Equation of Plane passing through the points (2, 2, -1) is
A(x – 2) + B(y – 2) + C(z + 1) = 0 ………………….. (1)
Since plane given by eqn. (1) passes through the points (3,4, 2) and (7, 0, 6)
Hence it will satisfy eqn. (2),
We get A(3 – 2) + B(4 – 2) + C(2 + 1) = 0
A + 2B + 3C = 0 ………………………. (2)
and A(7 – 2) + B(0 – 2) + C(6 + 1) = 0
5A – 2B + 7C = 0 …………………….. (3)
Solving eqns. (2) and (3),
img 39
\(\frac { A }{ 14+6 } \) = \(\frac { B }{ 15-7 } \) = \(\frac { C }{ -2-10 } \)
\(\frac { A }{ 20 } \) = \(\frac { B }{ 15-7 } \) = \(\frac { C }{ -2-10 } \)
\(\frac { A }{ 20 } \) = \(\frac { B }{ 8 } \) = \(\frac { C }{ -12 } \)
Let \(\frac { A }{ 5 } \) = \(\frac { B }{ 2 } \) = \(\frac { C }{ -3 } \) = k
A = 5k, B = 2k, C = -3k
Let \(\frac{A}{5}\) = \(\frac{B}{2}\) = \(\frac{C}{-3}\) = k
A = 5k, B = 2k, C = -3k
Putting in eqn.(1),
We get 5k(x – 2) + 2k(y – 2) + (-3k) (z + 1) = 0
k (5x + 2y – 3z – 17) = 0
5x + 2y – 3z – 17 = 0.
![]()
Question 15.
prove that the points (0, -1, -1), (4, 5, 1), (3, 9, 4) and (-4, 4, 4) are coplanar?
Solution:
Equation of plane passing through the points (0, -1, -1)
A(x – 0) + B(y + l) + C(z + 1) = 0 ………………………… (1)
It passes through the point (4, 5, 1)
A(4 – 0) + B(5 +1) + C(1 +1) = 0
⇒ 4A + 6B + 2C = 0
⇒ 2A + 3B + C = 0 ………………………………. (2)
Eqn. (1) also passes through (3, 9, 4),
A(3 – 0) + B(9 + 1) + C(4 + 1) = 0
⇒ 3A + 10B + 5C = 0 …………………………. (3)
Solving eqns. (2) and (3),
\(\frac { A }{ 15-10 } \) = \(\frac { B }{ 3-10 } \) = \(\frac { C }{ 20-9 } \) = k (let)
⇒\(\frac { A }{ 5 } \) = \(\frac { B }{ -7 } \) = \(\frac { C }{ 11 } \) = k
⇒ A = 5k, B = -7k, C = 11k
Putting in eqn. (1),
5k – 7k (y + 1) + 11k (z + 1) = 0
⇒ k(5x – 7y + 11z + 4) = 0
⇒ 5x – 7y + 11z + 4 = 0 ………………………… (4)
If the plane also passes through the point (-4, 4, 4) will satisfies eqn. (4),
5(- 4) – 7(4) + 11 (4) + 4 = 0
⇒ -20 – 28 + 44 + 4 = 0
⇒ 0 = 0
Hence given points are coplanar. Proved.
Question 16.
A variable plane \(\frac{x}{a}\) + \(\frac{y}{b}\) + \(\frac{z}{c}\) = 1 is at a distance 1 unit from origin. It cuts co – ordinate axes at A, B, C. The centroid (x, y, z) satisfies the equation \(\frac { 1 }{ x^{ 2 } } \) + \(\frac { 1 }{ y^{ 2 } } \) + \(\frac { 1 }{ z^{ 2 } } \) = k? Find the value of k?
Solution:
Given equation of plane \(\frac{x}{a}\) + \(\frac{y}{b}\) + \(\frac{z}{c}\) = 1
OA = a, OB = b, OC = c
The coordinates of the point A, B, C are (a, 0, 0), (0, b, 0) and (0, 0, c).
The length of perpendicular drawn from origin to the plane (1) is 1.
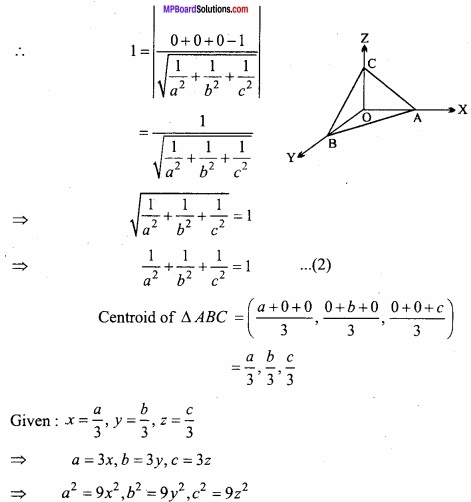
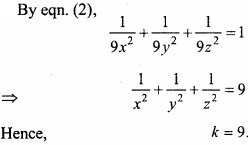
Question 17.
Find the equation of plane passing through the line of intersection of the planes x + 2y + 3z = 4 and 2x + y – z + 5 = 0 and perpendicular to the plane 5x + 3y + 6z + 8 = 0?
Solution:
Given planes
x + 2y + 3z = 4 ………………….. (1)
2x + y – z + 5 = 0 ………………… (2)
Equation of plane passing through the line of intersection of the planes (1) and (2)
x + 2y + 3z – 4 + λ(2x + y – z + 5) = 0 …………………. (3)
⇒ (1 + 2λ)x + (2 + λ)y + (3 – λ)z = 0
⇒ 10λ + 3λ – 6λ + 5 + 6 + 18 = 0
⇒ 7λ + 29 = 0
⇒ λ = \(\frac{-29}{7}\)
Putting the value of A in eqn. (3),
x + 2y + 3z – 4 – \(\frac{-29}{7}\) (2x + y – z + 5) = 0
⇒ 7x + 14y + 21z – 28 – 58x – 29y + 29z – 145 = 0
⇒ -51x – 15y + 50z – 173 = 0
⇒ 51x + 15y – 50z + 173 = 0.
![]()
Question 18.
Find the equation of plane passes through the line \(\frac { x-3 }{ 2 } \) = \(\frac { y+2 }{ 9 } \) = \(\frac { z-4 }{ -1 } \) and point (-6, 3, 2)?
Solution:
Point on given line D (3, -2,4)
∴ Eqn. of plane passing through point (3, -2, 4) is
A(x – 3) + B(y + 2) + C(z – 4) = 0 ……………………….. (1)
Plane (1) passes through point (-6, 3, 2),
– 9A + 5B – 2C = 0 …………………………. (2)
Direction ratio’s of given line is 2, 9, -1 and is parallel to plane (1),
2A + 9B – C = 0 ………………………. (3)
Now,
– 9A + 5B – 2C = 0
2A + 9B – C = 0
\(\frac { A }{ -5+18 } \) = \(\frac { B }{ -4-9 } \) = \(\frac { C }{ -81-10 } \)
⇒ \(\frac { A }{ 13 } \) = \(\frac { B }{ -13 } \) = \(\frac { C }{ -91 } \) = k
⇒ \(\frac { A }{ 1 } \) = \(\frac { B }{ -1 } \) = \(\frac { C }{ -7 } \) = k
A = k, B = -k, C = – 7k
Putting in eqn.(1), we get,
k(x – 3) – k (y + 2) – 7k(z – 4) = 0
⇒ x – y – 7z – 3 – 2 + 28 = 0
⇒ x – y – 7z + 23 = 0.
Question 19.
Find the vector equation of the line passing through (1,2,3) and parallel to the planes \(\vec { r } \). ( \(\hat { i } \) – \(\hat { j } \) + 2\(\hat { k } \) = 5 and \(\vec { r } \).(3\(\hat { i } \) + \(\hat { j } \) + \(\hat { k } \) ) = 6? (NCERT)
Solution:
Equation of line is:

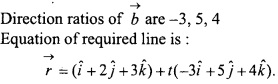
Question 20.
Find the vector equation of the line passing through the point (1, 2, -4) and perpendicular to the two lines
\(\frac { x-8 }{ 3 } \) = \(\frac { y+19 }{ -16 } \) = \(\frac { z-10 }{ 7 } \) and \(\frac { x-8 }{ 3 } \) = \(\frac { y-20 }{ 8 } \) = \(\frac { z-5 }{ -5 } \)? (NCERT)
Solution:

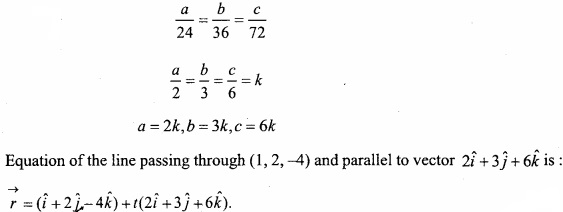
Question 21.
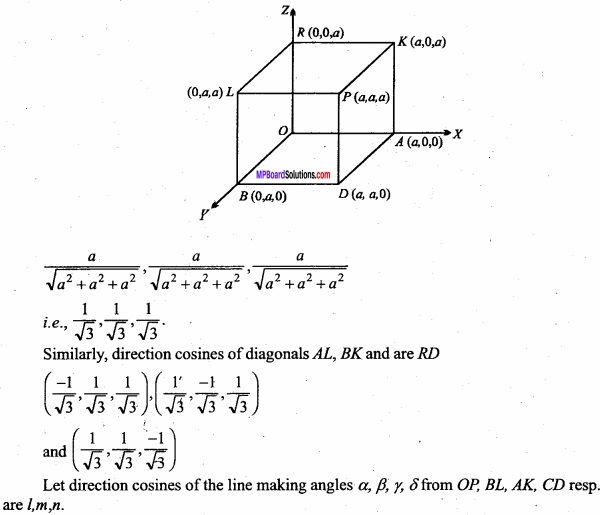
A line makes angles α, β, γ and and with four diagonals of a cube then prove that:
cos2α + cos2β + cos2 = \(\frac{4}{3}\)
Solution:
Taking three adjacent edges OA, OB, OC of the cube of side a as coordinate the coordinates of vertices of the cube are :
0 (0,0,0), A (a,0,0), B (0,a,0), R (0,0,a),
D (a,a,0), K (a,0,a), L (0,a,a), P (a,a,a)
Direction ratio of diagonal are a – 0, a – 0, a – 0, a, a, a direction cosines of OP are: