MP Board Class 12th Maths Important Questions Chapter 1 Relations and Functions
Relations and Functions Important Questions
Relations and Functions Objective Type Questions:
Question 1.
Choose the correct answer:
Question 1.
Let f : R → R te a function defined as f(x) = 8x:
(a) f is one – one onto (c) / is one-one but not onto
(b) f is many – one onto
(c) f is one – one but not onto
(d) f is neither one – one nor onto
Answer:
(a) f is one – one onto (c) / is one-one but not onto
Question 2.
Let f : R → R be a function is defined as f (x) = \(\frac { e^{ x^{ 2 } }-e^{ -x^{ 2 } } }{ e^{ x^{ 2 } }+e^{ -x^{ 2 } } } \):
(a) f is one – one but not onto
(b) f is one – one onto
(c) f is neither one – one nor onto
(d) f is many one onto
Answer:
(a) f is one – one but not onto
Question 3.
If f : R → R be given by f(x) = \((3-x^{ 3 })^{ 1/3 }\) then (fof) x is:
(a) x \(x^{ 1/3 }\)
(b) x\(x^{ 3 }\)
(c) x
(d) \((3-x^{ 3 })\)
Answer:
(c) x
![]()
Question 4.
Consider a binary operation * on N defined as a*b = \(a^{ 3 }\) + \(b^{ 3 }\):
(a) Is * both associative and commulative
(b) Is * commutative but not associative
(c) Is * associative but not commutative
(d) Is * neither commutative nor associative
Answer:
(b) Is * commutative but not associative
Question 5.
Number of binary operations on the set {a,b} are:
(a) 10
(b) 16
(c) 20
(d) 8
Answer:
(b) 16
Question 2.
Fill in the blanks:
- Number of equivalance relation in the set {1, 2, 3} containing (1,2) is …………………………….
- If f : R → R, when f(x) = 5x – 7,∀x∈R, then value of \(f^{ -1 }\) (7) is ……………………….
- If f : R → R, be defined by f(x) = x2 – 3x + 2, then f {f(x)} ……………………………
- If f : R → R, be defined by f(x) = 2x + 5, then \(f^{ -1 }\) (y) ………………………………
- If f : R → R, be defined by f(x) = x3 the f is ………………………………….
Answer:
- 2
- 0
- x4 – 6x3 + 10x2 – 3x
- \(\frac{1}{2}\) (y – 5)
- Is one – one
Question 3.
Write True/False:
- Let R = {(1, 3), (3, 1), (3, 3)} be a relation defined on A = {1, 2, 3}. Then R is symmetric, transitive but not reflexive.
- If f : A → B is bijective function, then the inverse of \(f^{ -1 }\) of f is unique.
- The composition of funtion is commutative
- Every function is invertible
- Let a binary operation * on the set Q+ of positive rational numbers be defined by a*b = \(\frac{ab}{3}\), ∀a,b ∈ Q+. Then the inverse of 4*6 is \(\frac{9}{8}\)
Answer:
- False
- True
- False
- False
- True
![]()
Question 4.
Write the answer in one word/sentence:
- Write the identity relation on the set A = {a, b, c}
- What is the range of the function f(x) = \(\frac{|x – 1|}{x – 1}\)?
- Write the domain of real valued function f defined by f(x) = \(\sqrt { 25-x^{ 2 } } \)
- Let * be a binay operation defined by a*b = 3a + 4b – 2, then find 4*5
- Let fg : R → R, defined f(x) = 2x + 1 and g(x) = x2 – 2, ∀x ∈ R respectively. Then find fog.
Answer:
- {(a,a), (b,b), (c,c)}
- {-1,1}
- [-5,5]
- 30
- 4x2 + 4x – 1
Relations and Functions Long Answer Type Questions – I
Question 1.
Show that the relation R in set Z of integers given by R = {(a, b) : 2 divides a – b} is an equivalence relation? (NCERT)
Solution:
R is reflexive as 2 divides (a – a) for all Z.
Let (a,b) ∈ R ⇒ 2, divides (a – b)
⇒ 2,divides – (b – a)
(a,b) e R ⇒ (b,a) ∈ R
∴R is symmetric.
Let (a,b) ∈ R ⇒ 2, divides (a -b)
(b,c) ∈ R ⇒ 2, divides (b – c)
(a – b) and (b – c), are divisible by 2
(a – b) + (b – c), are divisible by 2
Hence (a – c) is also divisible by 2
∴ (a,b) ∈ R,(b,c) ∈ R ⇒ (a,c) ∈ R
∴ R is transitive.
∴ R is reflexive, symmetric and transitive. Therefore R is an equivalence relation in Z. Proved.
Question 2.
Let R be the relation defined in the set A = {1,2,3,4, 5,6,7} by R = {(a, b): both a and b are either odd or even}
Show that R is an equivalence relation. Further, show that all the elements of the subset {1,3,5,7} are related to each other and all the elements of the subset {2,4,6} are related to each other but no element of the subset {1,3,5, 7} is related to any element of the subset {2,4, 6}? (NCERT)
Solution:
Given any element a in A, both a and a must be either odd or even. So that (a, a) ∈ R .
Further (a,b) ∈ R ⇒ both a and b must be either odd or even (a,b) ∈ R
Similarly (a,b) ∈ R (b,c) ∈ R ⇒ all the elements of the a, b, c must be either even or odd simultaneously ⇒ (a,c) ∈ R .
Hence R is an equivalence relation.
All elements of {1,3,5,7} are related to each other, as all the elements of this subset are odd. Similarly, all the elements of the subset {2, 4, 6} are related to each other(MPBoardSolutions.com) as all of them are even. Also no elements of the subset{ 1, 3, 5, 7} can be related to any elements of {2,4, 6} as elements of {1, 3, 5, 7} are odd, while elements of {2, 4, 6} are even.
Question 3.
Let N is set of natural numbers. If R is a relation defined in set N × N such that (a, b) R (c, d). If ad (b + c) = bc (a + d). Prove that R is an equivalence? (CBSE 2015)
Solution:
Reflexive: For every (a,b) ∈ N × N
ab (b + a) = ba (a + b)
⇒ (a, b) R {a, b)
∴ R is reflexive.
Symmetric: Let (a,b) (c,d) ∈ N × N
(a,b) R (c,d) ⇒ ab(b + c) = bc (a + d)
⇒ bc (a + d) = ab(b + c)
(a,b) R (c,d) ⇒ (c,d) R (a,b)
∴ R is symmetric.
Transitive:
Let (a, b) R(c,d) and (c, d) R (e,f)
⇒ ad (b + c) = bc (a + d)
and cf (d + e) = de (c+f)
⇒ \(\frac{ad (b+c)}{abcd}\) = \(\frac{bc (a+d)}{abcd}\)
and \(\frac{cf(d+e)}{cdef}\) = \(\frac{de(c+f)}{cdef}\)
⇒ \(\frac{1}{c}\) + \(\frac{1}{b}\) = \(\frac{1}{d}\) + \(\frac{1}{a}\)
and \(\frac{1}{e}\) + \(\frac{1}{d}\) = \(\frac{1}{f}\) + \(\frac{1}{c}\)
⇒ \(\frac{1}{c}\) + \(\frac{1}{b}\) + \(\frac{1}{e}\) + \(\frac{1}{d}\) = \(\frac{1}{d}\) + \(\frac{1}{a}\) + \(\frac{1}{f}\) + \(\frac{1}{c}\), (by adding)
⇒ \(\frac{1}{b}\) + \(\frac{1}{e}\) = \(\frac{1}{a}\) + \(\frac{1}{f}\)
⇒ \(\frac{b+e}{be}\) = \(\frac{a+f}{af}\)
⇒ af (b+e) = be (a+f)
(a,b) R (c,d) R (e,f) ⇒ (a,b) R (e,f)
∴ R is transitive
∴ R is reflecxive, symmetric and transitive, hence, equivalence.
![]()
Question 4.
Let A = {1,2,3,4,5} and R = {(a, b) : |a – b| is divided by 2}. Prove that R is an equivalence relation. Also form equivalence class?
Solution:
A = { 1, 2, 3,4, 5 } and R = {(a, b ) : |(a – b) is divisible by 2}
R = {(1, 1), (2,2), (3,3), (4,4), (5,5), (1,3), (1,5), (2,4), (3,5), (3,1) (5,1), (4,2),(5,3)}
∀a eA(a,a) E R R is reflexive.
Since (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) ∈ R
(a,b) ∈ R ⇒ (b,a) ∈ R
(1, 3), (1, 5), (2,4), (3, 5), (3, 1), (5, 1), (4, 2), (5, 3) ∈ R
∴ R is symmetric.
∀(a,b) ∈ R, (b,c) ∈ R ⇒ (a,c) ∈ R
Since (1,3), (3,1) ∈ R ⇒ (1,1) ∈ R
R is transitive.
R is reflexive, symmetric and transitive, hence R is equivalence. Proved.
Equivalence class:
[1] = { a : a and 2 is divided by |a – 1|}
[1] = {a : a ∈ A and a – 1 = 2 k}
[1] = {1, 3, 5}
[2] = { a : a and 2, is divided by |a – 2 |}
[2] = {a : a and a – 2 = 2k}
[2] = {2,4}. Proved.
Question 5.
Let for all n ∈ N

defines a function f : N → N.
Tell, is the function f one – one onto? Justify your answer also? (NCERT)
Solution:
In f : N → N
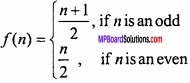
f (1) = \(\frac{1+1}{2}\) = 1
f (2) = \(\frac{2}{2}\) = 1
Here, f (1) = f (2) ⇒ 1 ≠ 2.
In co – domain there is only one image 1 of the two elements 1 and 2 of domain. Hence, f is not an one – one function.
Case I.
When n is odd
n = 2r + l, r ∈ N
Then, 4r + 1 ∈ N exists such that,
f (4r + 1) = \(\frac{4r+1+1}{2}\) = \(\frac{4r+2}{2}\) = 2r + 1.
Clearly, there is a pre – image in domain of the each element of co – domain. Hence, f is onto function.
Case II.
When n = 2r (even number)
Then, 4r ∈ N exists such that,
f (4r) = \(\frac{4r}{2}\) = 2r
Clearly, there is a pre – image in domain of the each element of co – domain.
Hence, f is onto function.
Thus, f is one – one onto function
Question 6.
Let A = R – {3} and B = R – {1}. Discuss the function f : A → B defined by f (x) = \(\frac{x-2}{x-3}\), is the function is one – one and onto? Justify your answer also? (NCERT)
A = R – {3} and B = R – {1}.
Solution:
f: A → B, f(x) = \(\frac{x-2}{x-3}\) , A = R – {3} and B = R – {1}.
Let x,y ∈ A is such that,
f (x) = f (y)
⇒ \(\frac{x-2}{x-3}\) = \(\frac{y-2}{y-3}\)
⇒ (x – 2) (y – 3) = (y – 2) (x – 3)
⇒ xy – 3x – 2y + 6 = xy – 3y – 2x + 6
⇒ – 3x – 2y = – 3y – 2x
⇒ x = y
Here, f(x) = f(y) ⇒ x = y.
∴ f is one – one function.
Let y ∈ B = R – {1}
f is onto if, x ∈ A is such that,
f (x) = y
\(\frac{x-2}{x-3}\) = y
⇒ x – 2 = y (x-3)
⇒ x – 2 = xy – 3y
⇒ xy – x = xy – 3y – 2
⇒ x (y – 1) = 3y – 2
⇒ x = \(\frac{3y-2}{y-1}\) ∈ A
For each y ∈ B, x ∈ A, then

f (x) = y
∴ f(x) is onto function,
∴ f is one – one function.
Question 7.
Prove that function defined below f : N → N is one – one and onto: (NCERT)
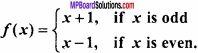
Solution:
Let f(x1) = f(x2)
If x1 is odd and x2 is even, then
x1 + 1 = x2 – 1
x1 – x2 = – 2
Which is impossible.
There is no chance that x1 is even and x2 is odd.
Hence either x1 and x2 both are even or odd.
Let x1, x2 both are odd.
f(x1) = f(x2)
⇒ x1 + 1 = x2 + 1
⇒ x1 = x2
Let x1 and x2 both are even.
f(x1) = f(x2)
⇒ x1 – 1 = x2 – 1
⇒ x1 = x2
∴ f is one – one
Odd number 2r + 1 of co – domain N is image of number 2r + 2 of N and any even number of co – domain N. i.e; 2r is image of number 2r – 1 of N.
∴ f is onto.
![]()
Question 8.
Discuss on function given by f(x) = 4x + 3, f : R →R. Prove that f is invertible. Find also the inverse of f? (NCERT)
Solution:
f : R → R, f(x) = 4x + 3
Domain and co – domain of the function is R.
Let, x,y ∈R are such that,
f(x) = f(y)
4x + 3 = 4y + 3
⇒ 4x = 4y
∴ x = y
Thus, f(x) = f(y) ⇒ x = y
f is one – one.
Let y is any element of co – domain R.
∴ y = f(x)
y = 4x + 3
⇒ 4x = y – 3
⇒ x = \(\frac{y – 3}{4}\)
y is real. Then, x = \(\frac{y – 3}{4}\) is also real. i.e., there is pre – image in domain of each of the element in co – domain.
i.e., range = co – domain
f is onto.
Hence, f is one – one and onto.
Let f – image of x is y. Then,
y = f(x)
y = 4x + 3, y ∈R
4x = y – 3, [f(x) = y ∴x \(f^{ -1 }\) (y)]
⇒ \(f^{ -1 }\) (y) = \(\frac{y – 3}{4}\)
∴ \(f^{ -1 }\) (x) = \(\frac{x – 3}{4}\)
Question 9.
Let y = {n2: n ∈ N] ⊂ N consider f : N → y as f(n) = n2 Show that/is invertible. Find the inverse of f? (NCERT)
Solution:
y = f(n) = n2
n = \(\sqrt { y } \)
From g(y) = \(\sqrt { y } \) is defined g : y → N.
gof (n) = g[f(n)]
= g[n2]
= \(\sqrt { n^{ 2 } } \). [ ∵g (n) = \(\sqrt { n } \) ⇒ g(n2) = \(\sqrt { n^{ 2 } } \) = n]
(gof) n = n
and (fog) y = f [g(y)]
= f \(\sqrt { y } \), [ ∵f (n) = n2 ⇒ f ( \(\sqrt { y } \)) = ( \(\sqrt { y } \))2 = y]
= y
Clearly, gof = In and fog = Iy
Hence, f is invertibel and f-1 = g. Proved.
Question 10.
If f : R → R and g : R → R are defined as f(x) = cosx and g(x) = 3x2. Find gof and fog. Prove that gof ≠ fog? (NCERT)
Solution:
Given:
f(x) = cosx
g(x) = 3x2
(gof) x = g[ f(x)]
(gof) x = g [cosx]
Given: f(x) = cos x …………….. (1)
g (x) = 3x2
g(cosx) = 3 cos2x
From eqns. (1) and (2)
(gof) x = 3 cos2x ………………. (2)
(fog) = f [g(x)]
= f [3x2] …………………….. (3)
Given: g(x) = 3x2
f (x) = cosx
f [3x2] = cos3x2 ………………………… (4)
From eqns. (3) and (4),
(fog)x = cos 3x2
For x = 0
3 cos2x ≠ cos 3x2
Hence, gof ≠ fog.
![]()
Question 11.
Let f : {1,2,3} → {a,b,c} given by f(1) = a, f(2) = b, f(3) = c. Find f-1 and show that (f-1)-1 = f?
Solution:
Given:
f : {1,2,3} → {a,b,c}
f(1) = a, f(2) = b, f(3) = c
Let g: {a,b,c} → {1,2,3}
g(a) = 1, g(b) = 2, g(c) = 3
(fog)a = f[g(a)]
= f[1] = a
(fog)b = f[g(b)]
= f(2) = b
(fog)c = f[g(b)]
= f(3) = c
and (gof) (1) = g[f(1)]
= g(a) = 1
(gof) (2) = g[f(2)]
= g(b) = 2
(gof) (3) = g[f(3)]
= g(c) = 3
Hence gof = Ix and fog = Iy
Where x = {1,2,3} and y = {a,b,c}
Inverse of f exists
and f-1 = g
∴ f-1 → {a,b,c} {1,2,3}
f-1(a) = 1, f-1(b) = 2, f-1(c) = 3
Now, find inverse of f-1 i.e.,g.
Let h : {1,2,3} → {a,b,c}
h(1) = a, h(2) = b, h(3) = c
(goh) 1 = g [h(1)] = g(a) = 1
(goh) 2 = g [h(2)] = g(b) = 2
(goh) 3 = g [h(3)] = g(c) = 3
and (hog) a = h[g(a)] = h(1) = a
(hog) b = h [g(b)] = h(2) = b
(hog) c = h [g(c)] = h(3) = c
∴ goh = Ix and hog = Iy
Where, x = {1,2,3} and y = {a,b,c}
Inverse of g exists and g-1 = h = (f-1)-1 = f
∴ h = f
∴ (f-1)-1 = f. Proved.
Question 12.
Show that the relation defined in the set A of all polygons as R = {(P1,P2): P1 and P2 have same number of sides } is an equivalence relation. (MPBoardSolutions.com) What is the set of all elements in A related of the right angle triangle T with sides 3,4 and 5? (NCERT)
Solution:
Given, A = set of all polygons
R = {(P1, P2): P1 and P2 have same number of sides}
In each polygon P the number of sides of polygon P are equal.
(P,P) ∈ R, ∀P ∈ A
Let (P1,P2) ∈ R
⇒ The number of sides in polygon P1 and Polygon P2 are same.
⇒ The sides of polygon P2 and polygon P1 are same.
(P1,P2) ∈ R ⇒ P2P1 ∈ R
∴ R is a symmetric relation.
Let (P1,P2) ∈ R and P2,P3) ∈ R.
The number of sides of polygon P1 and P2) are same.
∴ (P1,P2) ∈ R , (P2,P3) ⇒ (P1,P3) ∈ R
∴ Relation R is transitive.
The number of polygon realated with right angle traingle with sides 3, 4, 5 be three. Hence polygon realted with right angles traingle with sides 3, 4, 5 is a traingle. Proved.
Question 13.
If f(x) = \(\frac{4x+3}{6x-4}\) , x ≠ \(\frac{2}{3}\) then, prove that for all x ≠ \(\frac{2}{3}\), fof(x) = x. What is inverse function of f?
Solution:
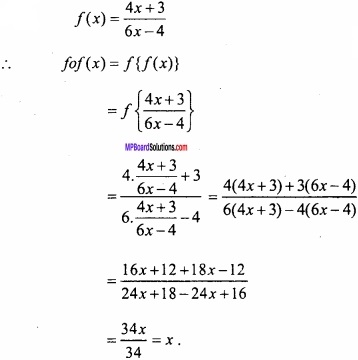
Let, inverse function of f-1 (x) = y .
Then f(y) = x
∴ \(\frac{4y+3}{6y-4}\) = x
⇒ 4y +3 = 6xy – 4x
⇒ 6xy – 4y = 3 + 4x
⇒ y (6x – 4) = 3 + 4x
⇒ y = \(\frac{3+4x}{6x-4}\)
⇒ f-1 (x) = \(\frac{3+4x}{6x-4}\) = f(x)
∴ f-1 = f.
Question 14.
Prove that the function given by f : [-1,1] → R, f(x) = \(\frac{x}{x+2}\) is one – one. Find the inverse function of function f : [-1,1] → (Range of f).
Solution:
f(x) = \(\frac{x}{x+2}\)
f : [-1,1] → R
Here f(x) = f(y)
⇒ \(\frac{x}{x+2}\) = \(\frac{y}{y+2}\)
⇒ xy + 2x = xy + 2y
⇒ 2x = 2y
⇒ x = y
∴ f is one – one
Let f-1(x) = y
∴ f(y) = x
⇒ \(\frac{y}{y+2}\) = x
⇒ y = xy + 2x
⇒ y (1 – x) = 2x
∴y = \(\frac{2x}{1-x}\)
⇒ f-1(x) = \(\frac{2x}{1-x}\).
![]()
Question 15.
If f(x) = \(\frac{x}{1+|x|}\), ∀x ∈ R and g(x) = \(\frac{x}{1-|x|}\) , ∀x ∈ R where -1 < x < 1, then find gof and fog? Show that fog = gof?
Solution:
Given: f(x) = \(\frac{x}{1+|x|}\)
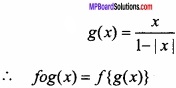
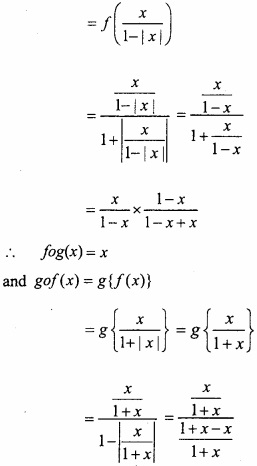
∴ gof (x) = x
∴ From eqns. (1) and (2),
fog = gof.
Question 16.
Consider f : N → N, g : N → N and h : N → R defined as f(x) = 2x, g(y) = 3y + 4 and h(z) = sin z ∀ x, y and z ∈ N. Show that ho(gof) = (hog)of? (NCERT)
Solution:
ho(gof) x = h[gof(x)]
= h[g[f(x)]
= h(g(2x))
= h[3(2x) + 4]
= h[6x + 4]
= sin (6x + 4) ……………………. (1)
Similarly, ((hog)of)x = (hog) f(x)
= (hog) 2x
= h(g(2x))
= h[3(2x) + 4]
= h [6x + 4]
= sin (6x + 4) ……………………… (2)
From eqns. (1) and (2),
ho(gof) = (hog)of. Proved.