MP Board Class 11th Physics Important Questions Chapter 9 ठोसों के यांत्रिक गुण 

Students get through the MP Board Class 11th Physics Important QuestionsChapter 9 ठोसों के यांत्रिक गुण which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 9 ठोसों के यांत्रिक गुण

अति लघु उत्तरीय प्रश्न

प्रश्न 1.
विरूपक बल से क्या समझते हो?
उत्तर-
किसी पिण्ड पर लगाये गये बाहरी बल को विरूपक बल कहते हैं।

प्रश्न 2.
विरूपण से क्या तात्पर्य है ?
उत्तर-
विरूपक बल के कारण पिण्ड में होने वाले परिवर्तन को विरूपण कहते हैं।

प्रश्न 3.
प्रत्यास्थता से क्या तात्पर्य है ?
उत्तर-
किसी पदार्थ का वह गुण जिसके कारण वह विरूपक बल द्वारा होने वाले परिवर्तन का विरोध करता है तथा बल को हटाये जाने पर अपनी पूर्वावस्था में आ जाता है।

प्रश्न 4.
प्रतिबल से क्या तात्पर्य है ?
उत्तर-
किसी वस्तु पर बाह्य बल लगाने पर प्रत्यास्थता के गुण के कारण वस्तु में एक बल उत्पन्न होता है जो इस परिवर्तन का विरोध करता है। इस बल को प्रत्यानयन बल कहते हैं और प्रत्यानयन बल का वह मान जो वस्तु के अनुप्रस्थ काट के एकांक क्षेत्रफल पर लगता है, प्रतिबल कहलाता है।

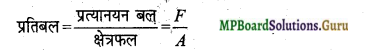
मात्रक-न्यूटन/मीटर- या डाइन/सेमी होता है।

प्रश्न 5.
अप्रत्यास्थ वस्तु से क्या तात्पर्य है ?
उत्तर-
किसी वस्तु का वह गुण जिसके कारण विरूपक बल लगाये जाने पर वस्तु स्थायी रूप से विकृत हो जाती है और अपनी प्रारंभिक अवस्था में वापिस नहीं आ पाती, अप्रत्यास्थता कहलाता है और ऐसी वस्तुएँ अप्रत्यास्थ वस्तुएँ कहलाती हैं।

प्रश्न 6.
प्रत्यास्थता की सीमा से क्या तात्पर्य है ?
उत्तर-
विरूपक बल का वह अधिकतम मान जिससे कम बल लगाने पर पदार्थ में प्रत्यास्थता का गुण बना रहता है तथा जिससे अधिक बल लगाने पर प्रत्यास्थता का गुणधर्म समाप्त हो जाता है, प्रत्यास्थता की सीमा कहलाती है।

प्रश्न 7.
भंगुरता से क्या तात्पर्य है ?
उत्तर-
किसी पदार्थ का वह गुण जिसके कारण प्रत्यास्थता सीमा से अधिक बल लगाने पर पदार्थ टुकड़ों में टूट जाता है, भंगुरता कहलाता है और ऐसी वस्तुएँ भंगुर वस्तुएँ कहलाती हैं।

प्रश्न 8.
प्रतिबल तथा दाब में क्या अन्तर है ?
उत्तर–
प्रतिबल आन्तरिक बल तथा दाब बाह्य बल है।

प्रश्न 9. विकृति से क्या तात्पर्य है ?
उत्तर-
विरूपक बल के कारण किसी वस्तु में एकांक विमा में होने वाले परिवर्तन को विकृति कहते हैं। यह एक विमाहीन राशि है।

प्रश्न 10.
प्रतिबल कितने प्रकार के होते हैं ? नाम लिखिए।
उत्तर-
प्रतिबल तीन प्रकार के होते हैं

• अनुदैर्ध्य प्रतिबल,
• अवमंदक प्रतिबल,
• आयतन प्रतिबल।

प्रश्न 11.
हुक का नियम लिखिए।
उत्तर-
हुक के नियमानुसार “प्रत्यास्थता की सीमा के अन्दर प्रतिबल, विकृति के अनुक्रमानुपाती होता है।” अर्थात्
प्रतिबल ∝ विकृति

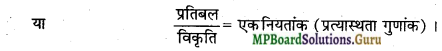
प्रश्न 12.
त्रोटन बल से क्या समझते हो ?
उत्तर-
किसी तार पर लगाया गया वह न्यूनतम बल जिससे तार टूटने लगता है तार के पदार्थ का त्रोटन बल कहलाता है। इससे अधिक बल लगाने पर तार की लंबाई बहुत शीघ्रता से बढ़ती है तथा तार बढ़ता हुआ प्रतीत होता है।

प्रश्न 13.
प्रत्यास्थता थकान से आप क्या समझते हो ?
उत्तर-
जब किसी तार पर कोई बल लंबे समय तक लगा रहता है तो तार अपनी अवस्था में वापिस लौटने में अधिक समय लेने लगता है, ऐसा लगने लगता है मानों तार थक गया है। यदि तार को कुछ समय तक विरूपक बल के प्रभाव से मुक्त रखा जाये तो वह पुन: पहले के समान प्रत्यास्थता के गुणों को प्रदर्शित करने लगता है। इस दोष को प्रत्यास्थता थकान कहते हैं।

प्रश्न 14.
अनुदैर्ध्य प्रतिबल किसे कहते हैं ?
उत्तर-
पिण्ड के जिस काट पर स्पर्शरेखीय प्रतिबल शून्य होता है उस काट के अभिलंब प्रतिबल को अनुदैर्ध्य प्रतिबल कहते हैं।

प्रश्न 15.
अपरूपण प्रतिबल किसे कहते हैं ?
उत्तर-
पिण्ड के जिस काट पर अभिलंब प्रतिबल शून्य होता है उस काट के स्पर्शरेखीय प्रतिबल को अपरूपण प्रतिबल कहते हैं।

प्रश्न 16.
आयतन प्रतिबल की परिभाषा दीजिए।
उत्तर-
पिण्ड के प्रत्येक काट का प्रतिबल जब काट के लंबवत् और बराबर होता है तब उसे आयतन प्रतिबल कहते हैं।

प्रश्न 17.
विकृति कितने प्रकार की होती है ?
उत्तर-
विकृति तीन प्रकार की होती है

1. अनुदैर्ध्य विकृति,
2. अपरूपण विकृति,
3. आयतन विकृति।

प्रश्न 18.
यंग प्रत्यास्थता गुणांक की परिभाषा तथा इसका सूत्र लिखिए।
उत्तर-
प्रत्यास्थता की सीमा के अन्दर अनुदैर्ध्य प्रतिबल तथा अनुदैर्ध्य विकृति के अनुपात को यंग प्रत्यास्थता गुणांक कहते हैं। इसे Y से प्रदर्शित करते हैं।
Y = \(\frac{M g L}{\pi r^{2} l}\)

प्रश्न 19.
आयतन प्रत्यास्थता गुणांक की परिभाषा लिखिये।
उत्तर-
प्रत्यास्थता की सीमा के अन्तर्गत अभिलंब प्रतिबल तथा आयतन विकृति के अनुपात को आयतन प्रत्यास्थता गुणांक कहते हैं। इसे K से प्रदर्शित करते हैं।
अतः
K = \(\frac{-P V}{\Delta V}\)

प्रश्न 20.
संपीड्यता से क्या समझते हो ?
उत्तर-
आयतन प्रत्यास्थता गुणांक के व्युत्क्रम को संपीड्यता कहते हैं।

प्रश्न 21.
ताँबा, लोहा, काँच तथा रबरको बढ़ती प्रत्यास्थता के क्रम में लिखिए।
उत्तर-
रबर < काँच < ताँबा < लोहा।

प्रश्न 22.
यदि हाथी दाँत तथा मिट्टी की एक जैसी गोलियाँ एक ही ऊँचाई से फर्श परगिरायी जायें तो फर्श से टकराने के बाद कौन-सी गोली अधिक ऊँचाई तक उठेगी और क्यों ?
उत्तर-
हाथी दाँत की गोली, क्योंकि इसकी प्रत्यास्थता सबसे अधिक है।

प्रश्न 23.
स्प्रिंग, ताँबे के बजाय लोहे की बनायी जाती है, क्यों?
उत्तर-
क्योंकि ताँबे की अपेक्षा लोहा अधिक प्रत्यास्थ है अतः समान विकृति के लिए लोहे की स्प्रिंग, ताँबे की स्प्रिंग की अपेक्षा अधिक विरूपक बल सहन कर सकती है।

प्रश्न 24.
प्रत्यानयन बल से क्या तात्पर्य है ?
उत्तर-
जिस बल के प्रभाव में वस्तु अपनी पूर्वावस्था ग्रहण करती है, उसे प्रत्यानयन बल कहते हैं।

प्रश्न 25.
प्रत्यानयन बल का विरूपक बल के बराबर और विपरीत होने का प्रतिबन्ध बताइये।
उत्तर-
जब वस्तु में विकृति प्रत्यास्थता की सीमा के अन्दर होती है तभी विरूपक बल, प्रत्यानयन बल के बराबर और विपरीत होता है।

प्रश्न 26.
ताप बढ़ाने पर यंग मापांक बढ़ता है या घटता है ?
उत्तर-
घटता है।

प्रश्न 27.
किसी तार को खींचने में कार्य क्यों करना पड़ता है ?
उत्तर-
एक तार को खींचने में अन्तः आण्विक दूरी बदलने पर अन्तः आण्विक बल क्रियाशील हो जाते हैं जिनके विरुद्ध कार्य करना पड़ता है।

प्रश्न 28.
किसी तार को खींचने में किये गये कार्य का क्या होता है ?
उत्तर-
तार को खींचने में किया गया कार्य तार में प्रत्यास्थ स्थितिज ऊर्जा के रूप में संचित हो जाता है।

प्रश्न 29.
किसी तार के लिए भंजक प्रतिबल से क्या तात्पर्य है?
उत्तर-
तार में प्रतिबल के अधिकतम् संभव मान को भंजक प्रतिबल कहते हैं।

प्रश्न 30.
किसी तार की लंबाई आधी करदी जाये तो उसके यंग प्रत्यास्थता गुणांक पर क्या प्रभाव पड़ेगा?
उत्तर-
कुछ नहीं क्योंकि यंग प्रत्यास्थता गुणांक तार के पदार्थ पर निर्भर करता है लंबाई पर नहीं।

प्रश्न 31.
एक तार की लंबाई काटकर आधी कर दी जाती है तो
(i) दिये गये भार के अन्तर्गत इसके लंबाई में वृद्धि पर क्या प्रभाव पड़ेगा?
उत्तर- लंबाई में वृद्धि पहले की आधी रह जायेगी।
(ii) अधिकतम भार पर जिसे तार सहन कर सकता है, क्या प्रभाव पड़ेगा?
उत्तर-
कोई प्रभाव नहीं पड़ेगा।

प्रश्न 32.
एक तार के स्थान पर उसी लंबाई तथा उसी पदार्थ का लेकिन दुगुने व्यास का एक अन्य तार लटकाया जाता है तो
(i) दिये गये भार के लिए लंबाई में वृद्धि कितनी रह जाएगी?
उत्तर-लंबाई में वृद्धि एक-चौथाई रह जाएगी।
(ii) अधिकतम भार पर जिसे तार वहन कर सकता है, क्या प्रभाव पड़ेगा?
उत्तर-
अधिकतम भार 4 गुना हो जायेगा।

प्रश्न 33.
एक केबिल को काटकर उसकी लंबाई आधी कर देने पर भी उसके द्वारा उठाये जा सकने वाले अधिकतम भार पर कोई प्रभाव नहीं पड़ता, क्यों?
उत्तर-
दिये गये पदार्थ के लिए भंजक प्रतिबल नियत रहता है तथा भंजक भार = भंजक प्रतिबल × अनुप्रस्थ काट का क्षेत्रफल।

प्रश्न 34.
क्या कारण है कि उपकरणों में निलंबन तार प्रायः क्वार्ट्ज या फास्फर ब्रांज के बनाये जाते हैं?
उत्तर-
क्योंकि क्वार्ट्ज और फास्फर ब्रांज में प्रत्यास्थ उत्तर प्रभाव नगण्य होता है।

प्रश्न 35.
लंबे समय तक प्रयोग में लाये जाने पर स्प्रिंग तुला अशुद्ध पाठ देने लगती है, क्यों ?
उत्तर-
लंबे समय तक प्रयोग में लाये जाने पर प्रत्यास्थता श्रांति के कारण स्प्रिंग का बल नियतांक कम हो जाता है अतः दिये गये भार के कारण अब स्प्रिंग में अधिक खिंचाव होता है जिससे वह अशुद्ध पाठ देती है।

प्रश्न 36.
यंग प्रत्यास्थता गुणांक नापने के प्रयोग में यदि तार की लंबाई दुगुनी ली जाये, तो यंग प्रत्यास्थता गुणांक के मान पर क्या प्रभाव पड़ेगा?
उत्तर-
यंग प्रत्यास्थता गुणांक के मान पर कोई प्रभाव नहीं पड़ेगा केवल समान भार के लिए उसकी लंबाई में वृद्धि पहले की अपेक्षा दुगुनी हो जायेगी।

प्रश्न 37.
किसी तार की धातु का यंग मापांक ज्ञात करते समय एक ही धातु के दो समान तार लटकाये जाते हैं, क्यों?
उत्तर-
ताकि प्रयोग करते समय वायुमंडल के ताप परिवर्तन का प्रभाव दोनों तारों पर समान रूप से पड़े।

प्रश्न 38.
क्या कारण है कि प्रत्यास्थता संबंधी प्रयोगों में तार से भार हटाते ही तुरन्त पाठ नहीं लेते अपितु कुछ देर ठहरने के बाद पाठ लेते हैं ?
उत्तर-
प्रत्यास्थता उत्तर प्रभाव का निराकरण करने के लिए।

प्रश्न 39.
किसी पदार्थ की प्रत्यास्थता पर ताप तथा अशुद्धि का क्या प्रभाव पड़ता है ?
उत्तर-
किसी पदार्थ का ताप बढ़ाने पर उसकी प्रत्यास्थता घट जाती है। किसी पदार्थ में उचित अशुद्धि मिलाने से वह अधिक प्रत्यास्थ हो जाती है।

लघु उत्तरीय प्रश्न

प्रश्न 1.
प्रत्यास्थ उत्तर प्रभाव से क्या तात्पर्य है ? क्या कारण है कि प्रत्यास्थता संबंधी प्रयोग में तार पर से भार हटाते ही तुरन्त पाठ नहीं लेते हैं बल्कि कुछ देर रुककर पाठ लेते हैं ?
उत्तर-
प्रत्यास्थता की सीमा के अन्दर भी बल लगाने के बाद उसे हटाने पर वस्तु को अपनी पूर्वावस्था में वापिस आने में कुछ समय लगता है। इसे प्रत्यास्थता उत्तर प्रभाव कहते हैं। यही कारण है कि प्रत्यास्थता संबंधी प्रयोग में तार पर से भार हटाते ही तुरन्त पाठ नहीं लेते हैं। बल्कि कुछ देर ठहरने के बाद पाठ लेते हैं ताकि तार अपनी पूर्वावस्था प्राप्त कर लेवे।

प्रश्न 2.
प्रत्यास्थ एवं प्लास्टिक वस्तुओं में अन्तर स्पष्ट कीजिए।
उत्तर-
वे वस्तुएँ जिन पर बल लगाने से उनकी लंबाई, आयतन, आकृति में कुछ परिवर्तन हो जाता है तथा बल को हटाने पर यह परिवर्तन स्वतः ही समाप्त हो जाता है और वस्तु पूर्ण रूप से अपनी पूर्वावस्था में आ जाती है, प्रत्यास्थ वस्तुएँ कहलाती हैं। क्वार्ट्ज़ को लगभग पूर्ण प्रत्यास्थ वस्तु माना जाता है।

वे वस्तुएँ जिन पर जब कोई बाह्य बल लगाया जाता है तो उनकी लंबाई, आयतन अथवा आकृति में कुछ परिवर्तन हो जाता है, परन्तु बल हटाने पर वे वापिस अपनी पूर्वावस्था में नहीं आती, प्लास्टिक वस्तुएँ कहलाती हैं। यद्यपि कोई भी वस्तु पूर्ण प्लास्टिक नहीं है। परन्तु फिर भी मोम का टुकड़ा पूर्ण प्लास्टिक माना जाता है।

प्रश्न 3.
यंग प्रत्यास्थता गुणांक का सूत्र लिखिये तथा इसके आधार पर यंग प्रत्यास्थता गुणांक की परिभाषा दीजिए इसका मात्रक तथा विमीय सूत्र भी लिखिए।
हल-यदि L लंबाई तथा A अनुप्रस्थ परिच्छेद वाले तार पर F बल लगाने से इसकी लंबाई में वृद्धि ! होती है तो यंग प्रत्यास्थता गुणांक
Y = \(\frac{F . L}{A . l}\)
A. अब यदि A = 1 वर्ग मीटर तथा l = L हो तो Y = F

अतः किसी पदार्थ का यंग प्रत्यास्थता गुणांक संख्यात्मक रूप से उस बल के बराबर होता है जो प्रत्यास्थता की सीमा में उस पदार्थ के एकांक परिच्छेद क्षेत्रफल वाले तार की लंबाई को दोगुना कर दे। यंग गुणांक का मात्रक न्यूटन / मीटर² है।

प्रश्न 4.
सिद्ध कीजिए कि स्टील, रबर से अधिक प्रत्यास्थ है।
उत्तर-
माना समान लंबाई L तथा समान त्रिज्या r के स्टील तथा रबर के दो तार हैं जिन पर समान बल F लगाने पर उनकी लंबाई में वृद्धि l_s तथा l_R होती हैं । यदि स्टील तथा रबर के यंग प्रत्यास्थता गुणांक क्रमशःY_s तथा Y_R हैं तो
Y_s = \(\frac{F \cdot L}{A l l_{S}}\) …………………….. (1)
एवं Y_R = \(\frac{F \cdot L}{A l_{R}}\) …………………… (2)

समी. (1) में समी. (2) का भाग देने पर,
\(\frac{Y_{S}}{Y_{R}}\) = \(\frac{l_{R}}{l_{s}}\) ………………………. (3)
परन्तु समान बल लगाने पर l_R>l_s
अतः समी. (3) से स्पष्ट है कि Y_s > Y_R
अतः स्टील, रबर से ज्यादा प्रत्यास्थ है।

प्रश्न 5.
यंग प्रत्यास्थता गुणांक से आप क्या समझते हैं ? इसके मात्रक तथा विमीय सूत्र लिखिये तथा इसके लिए सूत्र स्थापना कीजिये।
उत्तर-
प्रत्यास्थता की सीमा के अन्तर्गत अनुदैर्ध्य प्रतिबल तथा अनुदैर्ध्य विकृति के अनुपात को यंग प्रत्यास्थता गुणांक कहते हैं। अर्थात् img
इसका SI मात्रक न्यूटन / मीटर² तथा विमीय सूत्र [M¹L^-1T^-2] है।
माना एक तार की प्रारंभिक लंबाई L तथा त्रिज्या r है। उसके एक सिरे को दृढ़ आधार से कसकर दूसरे सिरे पर M द्रव्यमान का भार लटकाने पर उसकी लंबाई में वृद्धि । होती है।

अनुदैर्ध्य विकृति =\(\frac{l}{L}\)
यंग प्रत्यास्थता गुणांक = img
∴ Y = \(\frac{M g / \pi r^{2}}{l / L}\)
Y = \(\frac{M g L}{\pi r^{2} l}\)

प्रश्न 6.
आयतन प्रत्यास्थता गुणांक से क्या तात्पर्य है ? इसका सूत्र स्थापित कीजिए।
उत्तर-
प्रत्यास्थता की सीमा के अन्दर अभिलंब प्रतिबल तथा आयतन विकृति के अनुपात को आयतन प्रत्यास्थता गुणांक कहते हैं।

अनुदैर्ध्य विकृति माना किसी वस्तु का प्रारंभिक आयतन Vहै। उसकी किसी सतह पर अभिलंबवत् बल F लगाने से उसके आयतन में परिवर्तन Δ𝜏V हो जाता है। यदि उसकी सतह का क्षेत्रफल A हो तो
अभिलंब प्रतिबल =\(\frac{F}{A}\)
आयतन विकृति = – \(\frac{\Delta V}{V}\)
अतः आयतन प्रत्यास्थता गुणांक K = –\(\frac{\frac{F}{A}}{-\frac{\Delta V}{V}} \)
∴ K = –\(\frac{F . V}{A . \Delta V}\)
परन्तु \(\frac{F}{A}\) = P= दाब
अतः K= – \(\frac{P V}{\Delta V}\)

प्रश्न 7.
दृढ़ता गुणांक से क्या तात्पर्य है ? इसके लिए सूत्र स्थापित कीजिये।
उत्तर-
प्रत्यास्थता की सीमा के अन्तर्गत स्पर्शरेखीय प्रतिबल तथा अपरूपण विकृति के अनुपात को दृढ़ता गुणांक कहते हैं।
स्पर्शरेखीय प्रतिबल

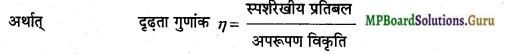
माना घनाभ ABCDEFGH के ऊपरी सतह ADEE जिसका क्षेत्रफल A है, पर स्पर्शरेखीय बल F लगाया जाता है जिससे समान्तर सतहों के मध्य कोणीय विस्थापन के Φ उत्पन्न हो जाता है।
अतः स्पर्शरेखीय प्रतिबल =\(\frac{F}{A}\)
तथा आयतन विकृति = Φ
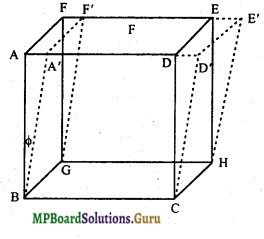
दृढ़ता गुणांक η = \(\frac{F}{\frac{A}{\phi}} \)
या η = \(\frac{F}{A \cdot \phi}\)

प्रश्न 8.
गर्डर लोहे के तथा I के आकार के क्यों बनाये जाते हैं ?
उत्तर-
माना किसी छड़ की लंबाई 1, चौड़ाई b तथा मोटाई d है। यदि इसके मध्य बिन्दु पर भार w लटका दिया जाये तो छड़ का झुकाव निम्न सूत्र द्वारा प्रदर्शित किया जाता है
δ = \(\frac{W l^{3}}{b d^{3} Y}\) ……………………. (1)

गर्डर की मजबूती के लिए आवश्यक है कि δ का मान कम हो। δ का मान कम होगा, यदि
(i) Y का मान अधिक हो अर्थात् प्रयुक्त धातु का यंग मापांक अधिक हो।
(ii) समी. (1) से स्पष्ट है कि δ ∝ \(\frac{1}{b}\) = तथा δ∝\(\frac{1}{d^{3}}\) अत: चौड़ाई 6 की तुलना में गहराई d को अधिक होना चाहिये।
उपर्युक्त कारणों से गर्डर, लोहे के तथा I आकार के बनाये जाते हैं।

प्रश्न 9.
पाइसन अनुपात से आप क्या समझते हैं ?
उत्तर-
प्रत्यास्थता की सीमा के अन्तर्गत अनुप्रस्थ विकृति और अनुदैर्ध्य विकृति के अनुपात को पाइसन अनुपात कहते हैं। इसे σ (सिग्मा) से प्रदर्शित करते हैं।

माना किसी तार के प्रारंभिक लंबाई L तथा व्यास D है। यदि लंबाई में । परिवर्तन होने पर उसके व्यास में परिवर्तन d हो, तो
पाइसन अनुपात σ = \(\frac{\frac{d}{D}}{\frac{l}{L}}\) = \(\frac{d L}{D I}\)
यह एक विमाहीन राशि है। इसका कोई मात्रक नहीं होता। इसका सैद्धान्तिक मान -1 से 0.5 होता है।

प्रश्न 10.
दो दृढ़ आधारों के बीच कसे हुए तार को ठंडा करने पर उत्पन्न होने वाले बल की गणना कीजिए।
उत्तर-
माना किसी तार की प्रारंभिक लंबाई L तथा उसके अनुप्रस्थ काट का क्षेत्रफल A है। इसे दो दृढ़ आधारों के बीच कस दिया गया है। जब उसे ठंडा किया जाता है तो उसमें संकुचन होता है अत: वह दृढ़ आधारों पर बल आरोपित करता है।

माना तार के पदार्थ का यंग मापांक Y तथा रेखीय प्रसार गुणांक a है। उसके ताप में ΔT की कमी करने पर उसकी लंबाई में होने वाली कमी । है। तब रेखीय प्रसार गुणांक की परिभाषा से,
α=\(\frac{l}{L . \Delta T}\) या l = α.LΔT
परन्तु Y=\(\frac{F \cdot L}{A \cdot l}\)
या F = \(\frac{Y A l}{L}\) = \(\frac{Y A \cdot \alpha \cdot L \Delta T}{L}\)
∴ F = YAαΔT

प्रश्न 11.
नीचे चित्र में किसी दिए हुए पदार्थ के लिए प्रतिबल-विकृति वक्र दर्शाया गया है। इस पदार्थ के लिए
(a) यंग प्रत्यास्थता गुणांक एवं
(b) सन्निकट पराभव सामर्थ्य (Yield strength) क्या है?
उत्तर-
(a) ग्राफ से स्पष्ट है कि 150 x 10⁶ N/m² प्रतिबल के लिए विकृति 0.002 है,

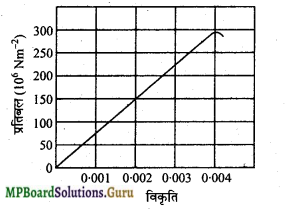
अत: यंग प्रत्यास्थता गुणांक

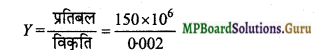
Y= 7.5 x 10¹⁰ N/m².
(b) किसी वस्तु का सन्निकट पराभव सामर्थ्य वह अधिकतम प्रतिबल है जिसे वह सहन कर सकता है। अतः ग्राफ से स्पष्ट है कि अधिकतम प्रतिबल का मान 300 x 10⁶ N/m² या 3 x 10⁸ N/m² है।

प्रश्न 12.
दो पदार्थों A एवं B के लिए प्रतिबल-विकृति ग्राफ चित्र में दर्शाए गए हैं। इन ग्राफों को एक ही पैमाना मानकर खींचा गया है

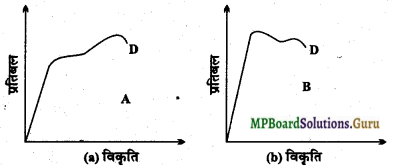
(a) किस पदार्थ का यंग प्रत्यास्थता गुणांक अधिक है।
(b) दोनों पदार्थों में कौन अधिक मजबूत है।
उत्तर-
(a) पदार्थ A का यंग प्रत्यास्थता गुणांक B के तुलना में अधिक है क्योंकि A का प्रतिबल B से अधिक है एवं A के लिए ग्राफ की ढाल (Slope) अधिक है।
(b) पदार्थ A, B के तुलना में अधिक मजबूत है क्योंकि A के लिए विखण्डन बिन्दु D के संगत प्रतिबल अधिक है।

प्रश्न 13.
किसी तार को खींचने में किये गये कार्य की गणना कीजिए।
अथवा
प्रत्यास्थ स्थितिज ऊर्जा का मान ज्ञात कीजिए।
उत्तर-
जब किसी तार को खींचा जाता है तो विरूपक बल के द्वारा उस पर कार्य किया जाता है। यह कार्य उस तार में स्थितिज ऊर्जा के रूप में संचित हो जाता है, जिसे तार की प्रत्यास्थ स्थितिज ऊर्जा कहते हैं।

माना किसी तार की प्रारंभिक लंबाई L, अनुप्रस्थ काट का क्षेत्रफल A तथा तार के पदार्थ का यंग मापांक Y है। उस पर विरूपक बल F लगाने पर उसकी लंबाई में वृद्धि | होती है।
प्रारंभ में तार पर लगने वाला बल 0 है जो बढ़कर F हो जाता है। अतः तार पर लगने वाला माध्य बल = \(\frac{0+F}{2}\) = \(\frac{F}{2}\)
कार्यरत है।
अतः तार को खींचने में किया गया कार्य = माध्य बल × लंबाई में वृद्धि
∴ W = \(\frac{F}{2}\) × l

अतः तार में संचित प्रत्यास्थ स्थितिज ऊर्जा U = \(\frac{1}{2}\) × F × l ………………………………. (1)
या समी. (1) को निम्नानुसार लिखा जा सकता है
U=\(\frac{1}{2}\) × \(\frac{F}{A}\) × \(\frac{l}{L}\) × F.A
या U =\(\frac{1}{2}\) × प्रतिबल × विकृति × आयतन ………………………………………………. (2)
अत: तार के प्रति एकांक आयतन में संचित प्रत्यास्थ स्थितिज ऊर्जा
U = \(\frac{1}{2}\) × प्रतिबल × विकृति ………………………………………….. (3)

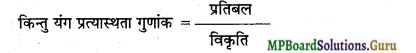
या प्रतिबल = यंग प्रत्यास्थता गुणांक × विकृति
समी. (1) में मान रखने पर,
U =\(\frac{1}{2}\) × यंग मापांक × (विकृति)2 ………………………………………. (4)
इसी प्रकार,

आंकिक प्रश्न

प्रश्न 1.
4.7 मीटर लंबे 3 × 10^-5 मीटर² अनुप्रस्थ काट के स्टील के तार तथा 3.5 मीटर लंबे व 4 × 10^-5 मीटर अनुप्रस्थ काट के ताँबे के तार पर दिए गए समान परिमाण के भारों को लटकाने पर उनके लंबाइयों में समान वृद्धि होती है। स्टील तथा ताँबे के यंग प्रत्यास्थता गुणांकों में क्या अनुपात है?
उत्तर-
हल-प्रश्नानुसार, स्टील के तार के लिए,
l₁ = 4.7 मीटर, A₁ = 3 × 10^-5 मीटर, तार पर लटकाए गये भार = F₁

अतः स्टील तार के लिए यंग प्रत्यास्थता गुणांक
Y₁ = \(\frac{\frac{F_{1}}{A_{1}}}{\frac{\Delta l_{1}}{l_{1}}}\) = \(\frac{\dot{F}_{1} l_{1}}{A_{1} \Delta l_{1}}\)

इसी प्रकार, ताँबे के तार के लिए यंग प्रत्यास्थता गुणांक
Y₂= \(\frac{F_{2} l_{2}}{A_{2} \Delta l_{2}}\)
या \(\frac{Y_{1}}{Y_{2}}\) = \(\frac{F_{1} l_{1}}{A_{1} \Delta l_{1}} \times \frac{A_{2} \Delta l_{2}}{F_{2} l_{2}} \)

या \(\frac{Y_{1}}{Y_{2}}\) = \(\frac{l_{1} A_{2}}{l_{2} A_{1}}\) ,(∵ F₁ = F₂ = F
एवं Δl₁ = Δl₂ = Δl)
∴ \(\frac{Y_{1}}{Y_{2}}\) = \(\frac{4 \cdot 7 \times 4 \times 10^{-5}}{3 \cdot 5 \times 3 \times 10^{-5}}\) = \(\frac{18.8}{10.5} \) = 1.79 ≈ 18:1.

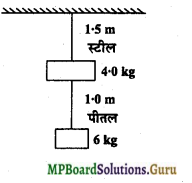
प्रश्न 2.
0.25 सेमी व्यास के दो तार, जिनमें एक इस्पात का तथा दूसरा पीतल का है, चित्र के अनुसार भारित है। बिना भार लटकाये इस्पात एवं
स्टील पीतल के तारों की लंबाइयाँ क्रमश: 1.5 मीटर तथा 1.0 मीटरहै। यदि इस्पात एवं पीतल के यंग गुणांक क्रमश: 2.0 × 10¹¹ Pa तथा 0.91 × 10¹¹Pa हो तो इस्पात एवं पीतल के तारों में विस्तार की गणना कीजिए।
उत्तर-
हल-प्रश्नानुसार, स्टील के तार के लिए,
लटकाये गए भार M₁g = (6 + 4) × 9.8 N = 10 × 9.8 = 98 N
l₁ = 1.5 m, r₁ = \(\frac{0 \cdot 25}{2}\) = 0.125cm = 0.125 x 10^-2m
Y₁ = 2.0 x 10¹¹ Pa

यंग प्रत्यास्थता गुणांक Y₁ = \(\frac{M_{1} g l_{1}}{\pi r_{1}^{2} \Delta l_{1}}\)
या Δl₁ = \(\frac{M_{1} g l_{1}}{\pi r_{1}^{2} Y_{1}}\) = \(\frac{98 \times 1.5}{3.14 \times\left(0-125 \times 10^{-2}\right)^{2} \times 2 \times 10^{11}}\)
∴ Δl₁ = 1.5 × 10^-4m

इसी प्रकार, पीतल के तार के लिए, लटकाये गए भार M₂g = 6 × 9.8 N .
l₂ = 1.0 m =\(\frac{0 \cdot 25}{2}\) = 0.125 cm = 0.125 x 10^-2 m
Y₂ = 0.91 × 10¹¹ Pa
∴ Δl₂= \(\frac{M_{2} g l_{2}}{\pi r_{2}^{2} Y_{2}}\) = \(\frac{6 \times 98 \times 1 \cdot 0}{3.14 \times\left(0 \cdot 125 \times 10^{-2}\right)^{2} \times 091 \times 10^{11}}\)
= 1.3 × 10^-4 m

प्रश्न 3.
ताँबे का एक टुकड़ा जिसका अनुप्रस्थ परिच्छेद 15.2mm × 19.1 mm का है, 44,500 N बल के तनाव से खींचा जाता है, जिसमें केवल प्रत्यास्थ विरूपण उत्पन्न हों। उत्पन्न विकृति की गणना कीजिए।
उत्तर-
हल-प्रश्नानुसार, A = 15.2 × 19.1 mm² = 15.2 × 19.1 × 10^-6 m²,
F= 44,500 N, यंग प्रत्यास्थता गुणांक, Y = 1.1 × 10¹¹ N/m²

प्रश्न 4.
1.5 सेमी त्रिज्या का एक इस्पात का केवल भार उठाने के लिए इस्तेमाल किया जाता है। यदिइस्पात के लिए अधिकतम अनुज्ञेय प्रतिबल 10⁸ N/m² है तो उस अधिकतम भार की गणना कीजिए जिसे केवल उठा सकता है।
उत्तर-
हल-प्रश्नानुसार, स्टील केबल की त्रिज्याr= 1.5 cm = 1.5 × 10^-2 m
अधिकतम प्रतिबल = 10⁸ N/m²
अधिकतम बल या भार = प्रतिबल × परिच्छेद का क्षेत्रफल
= 10⁸ × πr²
=10⁸ × 3.14 × 1.5 × 10^-2 × 1.5 × 10^-2N = 7.07 × 10⁴N.

प्रश्न 5.
4 मीटर लंबे तथा 1.2 सेमी² अनुप्रस्थ काट वाले ताँबे के तार को 4.8 × 10³ न्यूटन बल द्वारा खींचा जाता है। यदि ताँबे के लिए यंग प्रत्यास्थता गुणांक = 1.2 × 10¹¹ न्यूटन / मीटर है तो निम्न की गणना कीजिए-
(i) प्रतिबल,
(ii) विकृति,
(iii) तार की लंबाई में वृद्धि।
उत्तर-
हल-प्रश्नानुसार, L = 4 मीटर, A = 1.2 सेमी.² = 1.2 × 10^-4 मीटर
F= 4.8 x 10³ न्यूटन, Y = 1.2 × 10¹¹ न्यूटन/मीटर²

(i) प्रतिबल = \(\frac{F}{A}\) = \(\frac{4 \cdot 8 \times 10^{3}}{1 \cdot 2 \times 10^{-4}}\) = 4 ×10⁷N/m²

(ii) यंग प्रत्यास्थता गुणांक Y =

प्रश्न 6.
दो तार एक ही धातु के बने हुए हैं। प्रथम तार की लंबाई, द्वितीय तार की लंबाई की आधी है तथा उसका व्यास, दूसरे तार के व्यास का दोगुना है, यदि दोनों तारों पर समान भार लटकाया जाये तो उनकी लंबाइयों में हुई वृद्धि का अनुपात क्या होगा?
उत्तर-
हल-प्रश्नानुसार, L₁ = \(\frac{L_{2}}{2}\), d₁ = 2d₂
या r₁ = 2r₂
F₁ = F₂ तथा Y₁ = Y₂ (क्योंकि पदार्थ समान हैं)
∴ सूत्र Y= \(\frac{F L}{A l}\) = \(\frac{F L}{\pi r^{2} l}\) से.

लंबाई में वृद्धि l = \(\frac{F \cdot L}{\pi r^{2} Y}\)
∴ \(\frac{l_{1}}{l_{2}}\) = \(\frac{F_{1}}{F_{2}} \times \frac{L_{1}}{L_{2}} \times\left(\frac{r_{2}}{r_{1}}\right)^{2} \times \frac{Y_{2}}{Y_{1}}\)
या \(\frac{l_{1}}{l_{2}}\) = 1 × \(\frac{1}{2} \times\left(\frac{1}{2}\right)^{2}\) × 1 = \(\frac{1}{8}\)
या l₁:l₂ = 1 :8.

प्रश्न 7.
सोने के तार को खींचने पर इसकी लंबाई में वृद्धि 1% होती है। तार में रेखीय विकृति की गणना कीजिए। यदि सोने का यंग प्रत्यास्थता गुणांक 8 × 10¹⁰ न्यूटन / मीटर है तो तार पर प्रतिबल की गणना कीजिए।
उत्तर-
हल-प्रश्नानुसार लंबाई में वृद्धि l = 1% , Y = 8 ×10⁸N/m²

= (8 × 10¹⁰) × (0.01)
=8 × 10⁸ न्यूटन / मीटर²।

प्रश्न 8.
एक तार से 5 किग्रा का भार लटकाने पर उसकी लंबाई 8 मिमी बढ़ जाती है। यदि सभी बातें वही रहें परन्तु तार की त्रिज्या दोगुनी हो जाये तो अब लंबाई में कितनी वृद्धि होगी?
उत्तर-
हल- यंग मापांक Y =\(\frac{M g L}{\pi r^{2} l}\)
चूँकि सभी बातें वही रहती हैं (त्रिज्या को छोड़कर) तो r₁²l₁ = r^2₂l₂
दिया है- l₁= 8 मिमी, l₂ = ?, r₁= r तथा r₂
अतः l₂ = \(\frac{r^{2} \times 8}{(2 r)^{2}}\) = 2 मिमी। .

प्रश्न 9.
एक तार में 0.4 रेखीय विकृति उत्पन्न करने से 8 × 10¹⁰ न्यूटन / मीटर² का प्रतिबल उत्पन्न होता है। तार के पदार्थ का यंग मापांक ज्ञात कीजिए।
उत्तर-
हल-रेखीय विकृति = 0.4
रेखीय प्रतिबल = 8 ×10¹⁰ न्यूटन / मीटर²

Y = \(\frac{8 \times 10^{10}}{0 \cdot 4}\) =2 × 10¹¹ न्यूटन / मीटर²।

प्रश्न 10.
यदि 1.0 किग्रा /मिमी² का प्रतिबल एक तार पर लगाया जाये तो इसकी लंबाई में कितने प्रतिशत वृद्धि होगी ? Y = 1 x 10¹¹ न्यूटन /मीटर² तथा 1 किग्रा भार = 10 न्यूटन है।
उत्तर-
हल-प्रश्नानुसार, Y =1 x 10¹¹ न्यूटन / मीटर, 1 किग्रा भार =10 न्यूटन
प्रतिबल =\(\frac{F}{A}\) = 1 किग्रा / मिमी²
= \(\frac{1 \times 10 \times 9 \cdot 8}{10^{-6}}\) = 9.8 × 10⁷ N/m²
मानाकि L = 100 सेमी, I = ?

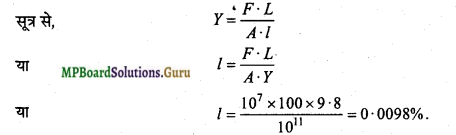
प्रश्न 11.
एक गोलाकार गेंद पर 100 वायुमंडल का दाब लंबवत् लगाने पर गेंद का आयतन 0.01% कम हो जाता है। गेंद के पदार्थ का आयतन प्रत्यास्थता गुणांक ज्ञात कीजिए। 1 वायुमंडल =1.01 x 10⁵ न्यूटन/मीटर²।
उत्तर-
हल-अभिलंब प्रतिबल = गैस पर आरोपित बल = 100 वायुमंडल
= 100 × (1.01 × 10⁵ N/m²) = 1.01 × 10⁷ न्यूटन / मी.²

=1.01 × 10¹¹N/m².

प्रश्न 12.
रबर की गेंद को 200 मीटर गहरी झील के ऊपरी तल से उसकी तली तक ले जाने में गेंद के आयतन में कमी 0.1% हो जाती है। झील के जल का घनत्व 1000 किग्रा/मी है। रबर का आयतन प्रत्यास्थता गुणांक ज्ञात कीजिए।(g = 9.8 मी/से) ।
उत्तर-
हल- गेंद को झील के ऊपरी तल में उसकी तली तक ले जाने में दाब में वृद्धि
P= hdg = 200 × 1000 × 9.8, = 196 × 10⁶N/m²
अतः अभिलंब प्रतिबल = 1.96 × 10⁶N/ m²
आयतन विकृति = 0.1% = \(\frac{0 \cdot 1}{100}\) = 10^-3

= \(\frac{1 \cdot 96 \times 10^{6}}{10^{-3}}\) = 1.96 × 10⁹ N/m².

प्रश्न 13.
20 किग्रा का भार एक तार से लटकाया गया है। तार का अनुप्रस्थ परिच्छेद क्षेत्रफल 1 मिमी है तथा तनी हुई अवस्था में इसकी लंबाई ठीक 6 मीटर है। भार हटा लेने पर लंबाई घटकर 5.995 मीटर रह जाती है। तार के पदार्थ का यंग प्रत्यास्थता गुणांक क्या होगा ?”
उत्तर-
हल-प्रश्नानुसार, M = 20 किग्रा, A=1 मिमी² = 10^-6 मीटर² , L = 6 मीटर
लंबाई में कमी l = 6 – 5.995 = 0.005 मीटर
सूत्र से Y = \(\frac{M g L}{A l}\)
या Y = \(\frac{20 \times 9 \cdot 8 \times 6}{10^{-6} \times 0 \cdot 05}\) = 2.35 × 10¹¹ N /m²

प्रश्न 14.
0.5 मिमी त्रिज्या के लोहे के तार को 300°C तक गर्म करके इसके दोनों सिरों को दो क्लैम्पों से कस दिया जाता है। यदि तार का ताप 30°C हो जाये तो क्लैम्प पर कितना बल लगेगा?
(लोहे का रेखीय प्रसार गुणांक = 1.2 × 10^-5/°C एवं Y = 1.4 × 10¹² डाइन/सेमी)
उत्तर-
हल-दिया है-r= 0.5 मिमी = 0.05 सेमी
α= 1.2 × 10^-5/°C
Y = 1.4 × 10¹² डाइन /सेमी²
ΔT = 300-30 = 270°C
F = YA αΔT से,
F = Y πr²ΔT
F = 1.4 × 10¹² × 3.14 x(0.05)² × 1.2 x 10^-5 × 270
= 3.56 × 10⁷ डाइन।

वस्तुनिष्ठ प्रश्न

1. सही विकल्प चुनकर लिखिए

प्रश्न1.
किसी तार की त्रिज्या r तथा लम्बाई L है। उस पर M द्रव्यमान का भार आरोपित करने पर उसकी लम्बाई में वृद्धि । होती है। यंग मापांक का मान होगा
(a) \(\frac{\mathrm{MgL}}{\pi r^{2} l}\)
(b) \(\frac{\mathrm{Mgl}}{\pi r^{2} \mathrm{~L}}\)
(c) \(\frac{\pi r^{2} \mathrm{~L}}{\mathrm{Mgl}}\)
(d) \(\frac{\pi r^{2} l}{M g L}\)
उत्तर-
(a) \(\frac{\mathrm{MgL}}{\pi r^{2} l}\)

प्रश्न 2.
कौन-सा पदार्थ अधिक प्रत्यास्थ है- ….
(a) काँच
(b) इस्पात
(c) प्लास्टिक
(d) रबर ।
उत्तर-
(b) इस्पात

प्रश्न 3.
पाइसन निष्पत्ति का मान किसके मध्य रहता है
(a) -1 व \(\frac{1}{2}\)
(b) \(\frac{3}{4}\) -व- \(\frac{1}{2}\)
(c) – \(\frac{1}{2}\) व 1
(d) 1 व 2.
उत्तर-
(a) -1 व \(\frac{1}{2}\)

प्रश्न 4.
एक प्रत्यास्थ तार के लिये प्रति एकांक आयतन में सम्पन्न कार्य है
(a) प्रतिबल × विकृति
(b) \(\frac{1}{2}\) × प्रतिबल × विकृति
(c) 2(प्रतिबल × विकृति)
(d) प्रतिबल/विकृति।
उत्तर-
(b) \(\frac{1}{2}\) × प्रतिबल × विकृति

प्रश्न 5.
निम्नलिखित चार तार एक ही पदार्थ के बने हैं, जब समान भार लटकाया जाता है तो किस तार की लम्बाई में सबसे अधिक वृद्धि होगी
(a) लम्बाई 50 सेमी तथा व्यास 0.5 मिमी
(b) लम्बाई 100 सेमी तथा व्यास 1 मिमी
(c) लम्बाई 200 सेमी तथा व्यास 2 मिमी
(d) लम्बाई 300 सेमी तथा व्यास 3 मिमी।
उत्तर-
(a) लम्बाई 50 सेमी तथा व्यास 0.5 मिमी

प्रश्न 6.
एक मिमी त्रिज्या के तार को तोड़ने के लिये 10 न्यूटन बल की आवश्यकता होती है। 3 मिमी त्रिज्या के तार को तोड़ने के लिये आवश्यक बल होगा- .
(a) 90 न्यूटन
(b) 1 न्यूटन
(c) 10 न्यूटन
(d) 30 न्यूटन ।
उत्तर-
(a) 90 न्यूटन

प्रश्न 7.
समान्यतः किसी वस्तु का दृढ़ता गुणांक उसके यंग प्रत्यास्थता गुणांक से
(a) कम होता है
(b) अधिक होता है
(c) बराबर होता है
(d) इनमें से कोई नहीं।
उत्तर-
(a) कम होता है

प्रश्न 8.
धातु की एक पत्ती की लम्बाई L, अनुप्रस्थ काट का क्षेत्रफल A, इसकी यंग प्रत्यास्थता । तथा रेखीय प्रसार गुणांक a है। इसे दो खम्भों के बीच बांधकर C तक गर्म किया। पट्टी पर लगने वाला बल होगा
(a) γAαa
(b) γAαLt
(c) tALα
(d) \(\frac{t \alpha \mathrm{L}}{\mathrm{A}}\)
उत्तर-
(a) γAαa .

2. रिक्त स्थानों की पूर्ति कीजिये-

1. प्रतिबल का मात्रक …………. है।
उत्तर-
न्यूटन/मीटर²

2. ताप बढ़ाने पर प्रत्यास्थता गुणांक का मान …………. होता है।
उत्तर-
कम

3. …………. में व्यावहारिक रूप से प्रत्यास्थ उत्तर प्रभाव नहीं होता है।
उत्तर-
क्वार्ट्ज

4. प्रत्यास्थता सीमा के भीतर …………. विकृति के अनुक्रमानुपाती होता है।
उत्तर-
प्रतिबल

5. पूर्ण दृढ़ वस्तु के पदार्थ का यंग मापांक …………. होता है।
उत्तर-
अनंत।

3. सत्य/असत्य बताइए

1. हुक का नियम प्रत्यास्थता सीमा के अन्दर ही लागू होता है।
उत्तर-
सत्य

2. हीरा को पूर्ण दृढ़ वस्तु माना जा सकता है।
उत्तर-
सत्य

3. यंग का प्रत्यास्थता गुणांक विमाहीन होता है।
उत्तर-
असत्य

4. प्रतिबल तथा विकृति का गुणनफल संचित ऊर्जा के बराबर होता है।
उत्तर-
असत्य

5. त्रोटन प्रतिबल तार के पदार्थ पर निर्भर करता है।
उत्तर-
सत्य

6. यंग प्रत्यास्थता गुणांक का अस्तित्व केवल ठोसों के लिए होता है।
उत्तर-
सत्य

7. रबर और इस्पात में रबर अधिक प्रत्यास्थ होता है।
उत्तर-
असत्य

8. हुक का नियम प्रत्यास्थता सीमा के लिये परिभाषित है।
tal
उत्तर-
असत्य

9. क्वार्ट्ज व्यावहारिक दृष्टि से प्रत्यास्थ उत्तर प्रभाव नहीं दर्शाता है।
उत्तर-
सत्य

10. एक छोटी छड़ की तुलना में एक लम्बी छड़ को मरोड़ना अधिक कठिन होता है।
उत्तर-
सत्य

11. समान लम्बाई और समान द्रव्यमान की एक खोखली छड़ ठोस छड़ की तुलना में अधिक मजबूत ……………………. होती है।
उत्तर-
सत्य।

4. सही जोड़ियाँ बनाइए

खण्ड ‘अ’	खण्ड ‘ब’
1. हुक का नियम	(a) क्षेत्रफल के अनुक्रमानुपाती
2. अभिलम्ब प्रतिबल	(b) शून्य
3. त्रोटन बल	(c) अपरूपण विकृति
4. प्लास्टिक वस्तु का यंग गुणांक	(d) प्रत्यास्थता सीमा के भीतर लागू होता है
5. स्पर्शी प्रतिबल	(e) आयतन विकृति।

उत्तर-
1. (d) प्रत्यास्थता सीमा के भीतर लागू होता है
2. (e) आयतन विकृति।
3. (a) क्षेत्रफल के अनुक्रमानुपाती
4. (b) शून्य
5. (c) अपरूपण विकृति.