MP Board Class 11th Maths Important Questions Chapter 8 Binomial Theorem
Binomial Theorem Important Questions
Binomial Theorem Objective Type Questions
(A) Choose the correct option :
Question 1.
The total number of terms in the expansion of
(a) 7
(b) 12
(c) 13
(d) 6.
Answer:
(c) 13
Question 2.
If y = 3x + 6x2 + 10x3 + …………… ∞, then the correct relation will be :
(a) x = 1 – (1 + y)–\(\frac { 1 }{ 3 }\)
(b) x = (1 + y)–\(\frac { 1 }{ 3 }\)
(c) y = 1 – (1 – x)-3
(d) x = 1 + (1 + y)–\(\frac { 1 }{ 3 }\)
Answer:
(a) x = 1 – (1 + y)–\(\frac { 1 }{ 3 }\)
Question 3.
The total number of terms in the expansion of (1+ x)-1 will be :
(a) 0
(b) ∞
(c) 2
(d) It can not be expand
Answer:
(b) ∞
![]()
Question 4.
The mid – term in the expansion of (x – \(\frac { 1 }{ x }\))10 will be :
(a) – 10C5
(b) 10C5
(c) 251
(d) 252
Answer:
(a) – 10C5
Question 5.
For all positive integer of n, n(n – 1) is :
(a) Integer
(b) Natural number
(c) Even positive integer
(d) Odd positive integer.
Answer:
(c) Even positive integer
Question 6.
Expansion of (a + x)n is :
(a) an + nC1an-1x + nC2an-2x2 + ……….. + nCran-rxr + ………… + an
(b) xn + nC1xn-1a +nC2xn-2a2 + ……….. + nCrxn-rar + ………… + an
(c) an – nC1an-1x + nC2an-2x2 + ……….. + (-1)rnCran-rxr + ………… + (-1)nan
(d) xn – nC1an-1a + nC2an-2a2 + ……….. + (-1)rnCran-rxr + ………… + (-1)nxn
Answer:
(a) an + nC1an-1x +nC2an-2x2 + ……….. + nCran-rxr + ………… + an
Question 7.
The fifth term in the expansion of ( x – \(\frac { 1 }{ x }\) )10 from the end, will be :
(a) \(\frac { ^{ 10 }{ C }_{ 6 } }{ x }\)
(b) \(\frac { 105 }{ 32{ x }^{ 2 } }\)
(c) \(\frac { ^{ 10 }{ C }_{ 6 } }{ { x }^{ 2 } }\)
(d) \(\frac { ^{ 10 }{ C }_{ 6 } }{ { x }^{ 10 } }\)
Answer:
(a) \(\frac { ^{ 10 }{ C }_{ 6 } }{ x }\)
[Hint: The total number of terms be 11 in the expansion of it.
∵ The 5th term from end = (11 – 5)th = 7th term from the beginning.]
Question 8.
The number of mid – terms in the expansion of ( x – \(\frac { 1 }{ x }\) )10
(a) 1
(b) 2
(c) – \(\frac { ^{ 13 }{ C }_{ 7 } }{ x }\)
(d) 1716x
Answer:
(b) 2
Question 9.
The value of nC0 + nC1 + nC2 + …………….. + nCn :
(a) 2n + 1
(b) 2n – 1
(c) 2n – 1
(d) 2n
Answer:
(d) 2n
Question 10.
The value of nC0 + nC2 + nC4 + …………….. = nC1 + nC3 + ……………. will be :
(a) 2n + 1
(b) 2n – 1
(c) 2n – 1
(d) 2n
Answer:
(b) 2n – 1
Question 11.
The total number of terms in the expansion of (a + b + c + d)n will be :
(a) \(\frac { (n+1)(n+2) }{ 2 }\)
(b) \(\frac { n(n+1) }{ 2 }\)
(c) \(\frac { (n+1)(n+2)(n+3) }{ 6 }\)
(d) \(\frac { (n+1)(n+2) }{ 6 }\)
Answer:
(c) \(\frac { (n+1)(n+2)(n+3) }{ 6 }\)
Question 12.
The necessary condition for expansion of (1 + x)-1 is :
(a) | x | < 1
(b) | x | > 1
(c) | x | = 1
(d) | x | = – 1.
Answer:
(a) | x | < 1
Question 13.
The general term in the expansion of (x + a)n will be :
(a) rth
(b) (r+1)thterm
(c) (r-1)th
(d) (r+2)thterm
Answer:
(b) (r+1)thterm
Question 14.
In the expansion of ( 2x + \(\frac { 1 }{ { 3x }^{ 2 } }\) )9, then term independent of x will be :
(a) \(\frac { 8 }{ 127 }\)
(b) \(\frac { 124 }{ 81 }\)
(c) \(\frac { 1792 }{ 9 }\)
(d) \(\frac { 256 }{ 243 }\)
Answer:
(c) \(\frac { 1792 }{ 9 }\)
Question 15.
The coefficient of x3 in the expansion of ( x – \(\frac { 1 }{ x }\) )15 is :
(a) 14
(b) 21
(c) 28
(d) 35
Answer:
(b) 21
Question 16.
The independent term in the expansion of (x2 – \(\frac { 2 }{ { x }^{ 3 } }\))15 is :
(a) 5th
(b) 6th
(c) 7th
(d) 8th
Answer:
(c) 7th
![]()
Question 17.
The value of nC0 + nC1 + nC2 + …………….. = nCn the expansion of (l + x)n is :
(a) 2n – 1
(b) 2n – 2
(c) 2n
(d) 2n-1
Answer:
(c) 2n
Question 18.
The value of 15C0 + 15C2 + 15C4 + 15C6 + …………….. = 15C14 is :
(a) 214
(b) 215
(c) 215 – 1
(d) None of these
Answer:
(a) 214
(B) Match the following :

Answer:
- (d)
- (a)
- (e)
- (c)
- (b)
- (g)
- (f)
- (i)
- (b)
(C) Fill in the blanks :
- By binomial theorem the value of (102)4 is ……………..
- The value of second term in the expansion of (1 – x)-3/2 is ……………..
- The 5th term from the end in the expansion of (x – \(\frac { 1 }{ 2x }\) )10 is ……………..
- The constant term will be …………….. in the expansion of ( x2 – 2 + \(\frac { 1 }{ { x }^{ 2 } }\) )6
- The value of C1 + 2C2 + 3C3 + ………….. + nCn will be ……………..
- The value of nC0 – nC1 + nC2 – nC3 + ………….. will be ……………..
- The value of
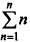 is ……………..
is …………….. - The value of
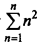 is ……………..
is …………….. - The value of
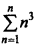 is ……………..
is …………….. - (2x + 3y)5 = …………….. up to three terms.
- The coefficient of x7 in the expansion of (x2 + \(\frac { 1 }{ x }\) )11 will be …………….
- In the expansion of (1 – x)10 the value of middle term is ……………..
- Third (3rd) term in the expansion of e-3x will be ……………..
- If n is odd, in the expansion of (x + a)n, then number of middle terms are ……………..
- The middle term in the expansion of (\(\frac { x }{ a }\) + \(\frac { a }{ x }\) )10
- The coefficient of xn in the expansion of (1 + x) (1 – x)n will be ……………..
Answer:
- 08243216
- \(\frac { { x }^{ 3 } }{ 16 }\)
- \(\frac { 105 }{ 32{ x }^{ 2 } }\)
- 924
- n.2n-1
- 0
- \(\frac { n(n+1) }{ 2 }\)
- \(\frac { n(n+1)(2n+1) }{ 6 }\)
- [ \(\frac { n(n+1) }{ 2 }\) ]2
- 32x5 + 240x4y + 720x3y2
- 462
- – 252 x-5
- \(\frac { 1 }{ 2 }\)
- Two
- 252
- (- 1)n(1 – n)
(D) Write true / false :
- The expansion of (1 + x)-3 is 1 – 3x + 6x2 – 10x3 + ………….. + \(\frac { (- 1)(r + 1)(r +2) }{ 2! }\)xr + ……………..
- The expansion of (1 – x)-3 is 1 + 3x + 6x2 + 10x3 + ………….. + \(\frac { (- 1)r(r + 1)(r +2) }{ 2! }\)xr + ……………..
- The expansion of (1 – x)-2 is 1 + 2x + 3x2 + (r + 1) xr+ ………….. +
- The (r + 1 )th term in the expansion of (1 – x)-2 is (- 1)r(r + 1) xr+ ………….. +
- The (r + 1 )th term in the expansion of (1 – x)n will be xr
- The total number of terms in the expansion of (a + b + c)n is \(\frac { (n + 1)(n + 1) }{ 2 }\)
- In the expansion of ( 3x – \(\frac { { x }^{ 3 } }{ 9 } \) )9, No . of terms is 9.
- The number of term in the expansion of ( 3x – \(\frac { { x }^{ 3 } }{ 9 } \) )9 is 8.
- In the expansion of (x + a)n then sum of powers of x and α in any term is n.
- The coefficient of x in the expansion of (1 – 2x)-3 is 6.
- The second term in the expansion of (2x + 3y)5 is 240x4y.
- The value of second term in the expansion of (1 – x)-3/2 is \(\frac { 3 }{ 2 }\)x.
Answer:
- True
- True
- True
- True
- False
- True
- False
- False
- True
- False
- True
- True.
(E) Write answer in one word / sentence :
- Find the value of 9993 by the binomial theorem
- Find the middle term in expansion of (x2 – \(\frac { 1 }{ x }\))6
- General term in the expansion of (x + a)n will be.
- If in the expansion of (1+x)51 the coefficient of xr and xr – 5 are equal, then the value of r will be.
- Find the coefficient of xn in the expansion of (1 + x + x2 + …………… ∞)2, if | x | < 1.
- In the expansion of (\(\frac { x }{ 3 }\) – \(\frac { 2 }{ { x }^{ 2 } }\))10, x4 comes in rth term, then the value of r will be.
- The 5th term in the expansion of (1 – 2x)– 1 will be.
Answer:
- 997002999
- – 20 x5
- nCr xn – r ar
- 28
- (n + 1)
- 3
- 16x2
Binomial Theorem Long Answer Type Questions
Question 1.
Expand : (\(\frac { 2 }{ x }\) – \(\frac { x }{ 2 }\))5 (NCERT)
Solution:

Question 2.
Expand : (2x – 3)6 (NCERT)
Solution:

Question 3.
Expand : (\(\frac { x }{ 3 }\) + \(\frac { 1 }{ x }\))5 (NCERT)
Solution:

Question 4.
Expand : (x + \(\frac { 1 }{ x }\))6. (NCERT)
Solution:

Question 5.
find 13th term in the expansion of ( 9x – \(\frac { 1 }{ 3\sqrt { x } }\) )18. (NCERT)
Solution:

Question 6.
Find the middle term of (3 – \(\frac { { x }^{ 3 } }{ 6 }\))7
Solution:

Question 7.
Find the middle term in the expansion of (\(\frac { x }{ 3 }\) + 9y)10
Solution:
Here n =10
Total number of terms = n + 1 = 10 + 1 = 11 (odd)
Here, the term will be middle term.

Question 8.
If coefficient of x2 and x3 in the expansion of (3 + ax)9 are equal, the value of a.
Solution:
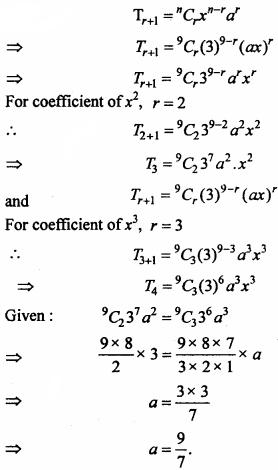
Question 9.
Find the coefficient of x5 in the expansion of (x + 3)8
Solution:
Suppose x5 appears in (r + 1)th term Tr+1 = nC1xn-rar
Here n = 8, x = x, a = 3
Tr+1 = 8Cr(x)8 – r(3)r
For the coefficient of x5,
8 – r = 5
=> r = 3
T3+1 = 8C3(3)3
= \(\frac { 8 × 7 × 6 }{ 3 × 2 × 1}\) × 3 × 3 × 3 × x5
= 1512 × x5
Hence coefficient of x5 is 1512.
![]()
Question 10.
Find the coefficient of a5b7 in the expansion of (a – 2b)12.
Solution:

Question 11.
If the 17th and 18th terms in the expansion of (2 + a)50 are equal, then find the value of a. (NCERT)
Solution:
In the expansion of (x + a)n
Tr+1 = nCr xn – r ar
Here n = 50, x = 2, a = a
T17 = T16 + 1 = 50C16 (2)50 – 16 (a)16
⇒ T17 = 50C16 (2)34 (a)16
and T18 = T17 + 1 = 50C17 (2)50 – 17 (a)17
= 50C17 (2)33 (a)17

Question 12.
Prove that the value of the middle term in the expansion of (1+x)2n is \(\frac { { 1.3.5 …….. (2n – 1)} }{ n! }\).2n xn
Solution:
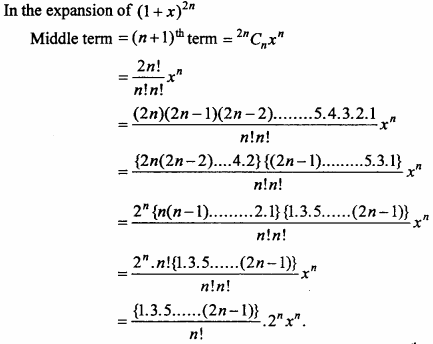
Question 13.
In the expansion of (x + 1)n, the coefficient of the (r – 1)th, rth and (r + 1)th terms are in the ratio 1 : 3 : 5, then find the value of n and r.
Solution:
In the expansion of (x + 1)n,
Tr + 1 = nCrxn – r(1)r
Tr – 1 = Tr – 2 + 1 = nCr – 2(x)n – (r – 2)(1)r – 2
Coefficient of Tr – 1th term = nCr – 2
Tr = Tr – 1 + 1 = nCr – 1(x)n – (r – 1)(1)r – 1
Coefficient of Trthterm = nCr – 1
Tr + 1 = nCr xn – r (1)r
Coefficient of Tr+1th term = nCr
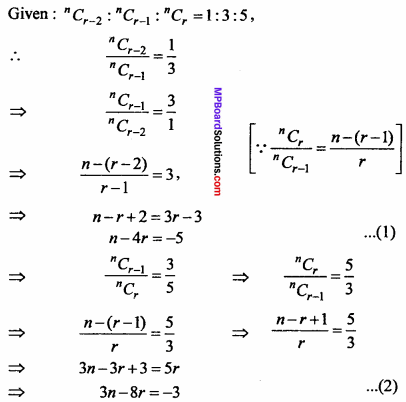
Put n = 4r – 5 from equation (1) in equation (2),
3(4r – 5) – 8r = – 3
⇒ 12r – 15 – 8r = – 3
⇒ 4r = 12
∴ r = 3
Put r = 3 in equation (2),
n – 4 x 3 = – 5
⇒ n = 12 – 5
⇒ n = l
n = 7, r = 3
Question 14.
Prove that the coefficient of xn in the expansion of (1 + x)2n of in the expansion of (1 + x)2n – 1.
Solution:
In the expansion of (x + a)n
Tr+1 = nCr xn – r ar
Here x = 1, a = x, n = 2n
Tr+1 = 2nCr(1)2n – r(x)r
For the coefficient of xn, put r = n,
Tn+1 = 2nCn(a)2n – n(x)n
and T18 = T17 + 1 = 50C17 (2)50 – 17 (a)17
= (2nCn) xn
∴ In the expansion of (1 + x)2n, the coefficient of xn = 2nCn …. (1)
and in the expansion of (1 + x)2n – 1, x = 1, a = x, n = 2n – 1
∴ Tr+1 = 2nCr (1)2n – 1 -r (x)n
For the coefficient of xn, put r = n, ‘
We get Tn+1 = 2n – 1Cn xn
The coefficient of xn in the expansion of (1 + x)2n – 1 = n – 1Cn
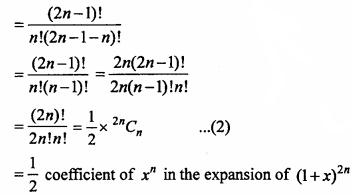
∴ The coefficient of xn in the expansion of (1 + x)2n
= 2 x The coefficient of xn in the expansion of (1 + x)2n, [from equation (1) and (2)]
Question 15.
Find the constant term in the expansion of (\(\frac { 3 }{ 2 }\)x2 – \(\frac { 1 }{ 3x }\))6
Solution:
