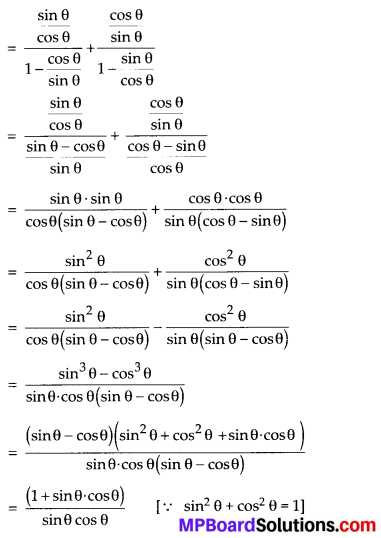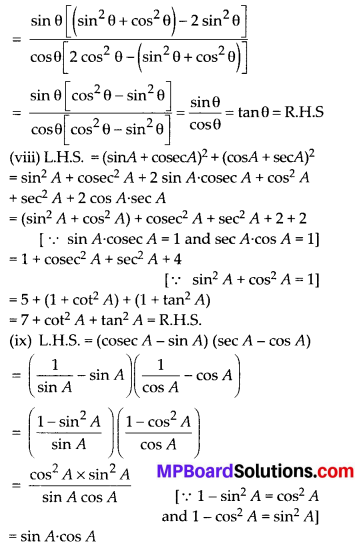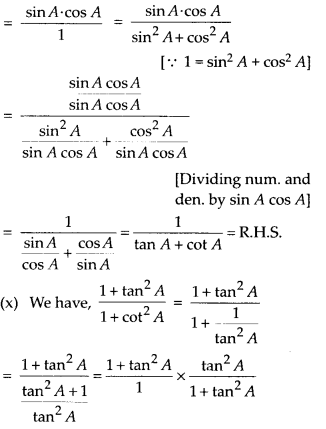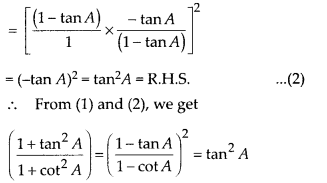In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 8 Introduction to Trigonometry Ex 8.4 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 8 Introduction to Trigonometry Ex 8.4
Question 1.
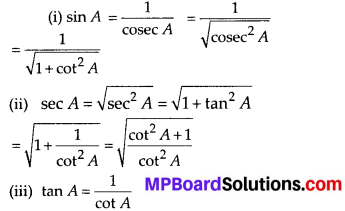
Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Solution:
Question 2.
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:
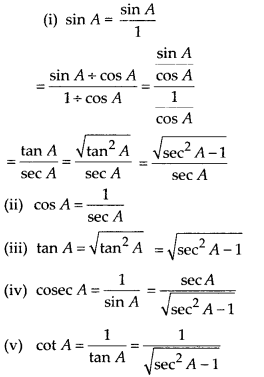
Question 3.
Evaluate:
(i) \(\frac{\sin ^{2} 63^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\cos ^{2} 73^{\circ}}\)
(ii) sin 25° cos 65° + cos 25° sin 65°
Solution:
(i) \(\frac{\sin ^{2} 63^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\cos ^{2} 73^{\circ}}\)
∵ sin 63° = sin (90° – 27°) = cos 27°
⇒ sin2 63° = cos2 27°
cos2 73° = cos2 (90° – 17°) = sin2 17°
∴ \(\frac{\sin ^{2} 63^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\cos ^{2} 73^{\circ}}=\frac{\cos ^{2} 27^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\sin ^{2} 17^{\circ}}=1\)
[ ∵ cos2 A + sin2 A = 1]
(ii) sin 25° cos 65° + cos 25° sin 65°
∵ sin 25° = sin (90° – 65°) = cos 65° [ ∵ sin (90° – A) = cos A]
cos 25° = cos (90° – 65°) = sin 65° [ ∵ cos (90° – A) = sin A]
∴ sin 25° cos 65° + cos 25° sin 65°
= cos 65° cos 65° + sin 65° sin 65°
= (cos 65°)2 + (sin 65°)2
= cos2 65° + sin2 65° = 1 [∵ cos2 A + sin2 A = 1]
![]()
Question 4.
Choose the correct option. Justify your choice.
(i) 9 sec2A – 9 tan2A =
(A) 1
(B) 9
(C) 8
(D) 0
(ii) (1 +tanθ + secθ) (1 + cotθ – cosec0) =
(A) 0
(B) 1
(C) 2
(D) – 1
(iii) (sec A + tan A) (1 – sinA) =
(A) sec A
(B) sin A
(C) cosec A
(D) cos A
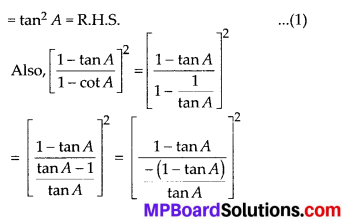
(iv) \(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}=\)
(A) sec2 A
(B) -1
(C) cot2 A
(D) tan2 A
Solution:
(i) (B): Since, 9 sec2 A – 9 tan2 A
= 9 (sec2 A – tan2 A) = 9 (1) = 9 [∵ sec2 A – tan2 A = 1]
(ii) (C): Here,

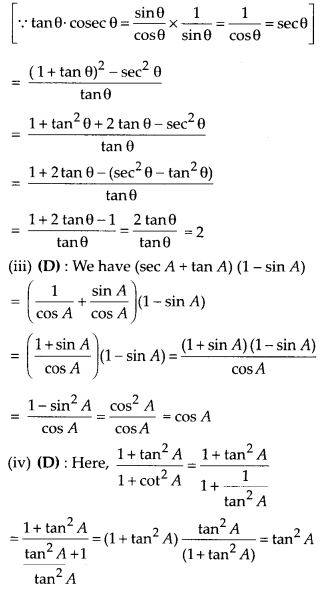
Question 5.
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

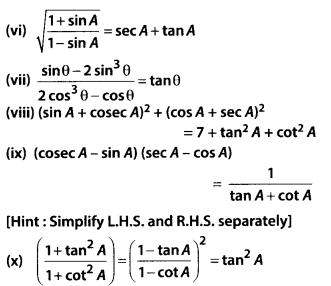
Solution: