MP Board Class 9th Maths Solutions Chapter 9 Areas of Parallelograms and Triangles Ex 9.3
Question 1.
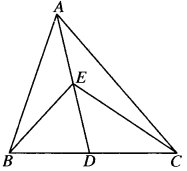
In Fig. given below E is any point on median AD of a ∆ABC. Show that ar (ABE) = ar (ACE).
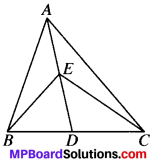
Solution:
Given.
E is any point on median AD of ∆ABC.
To prove
ar (ABE) = ar (ACE)
Proof:
In ∆ABC, AD is the median
ar (ABD) = ar(ACD) ….(1)
In ∆EBC, ED is the median
∴ ar (BDE) = ar (CDE) ….(2)
Subtracting (2) from (1), we get
ar (ABD) – ar (BDE) = ar (ACD) – ar (CDE)
ar (ABE) = ar (ACE)
![]()
Question 2.
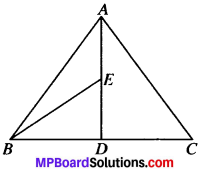
In a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = \(\frac{1}{4}\) ar (ABC).
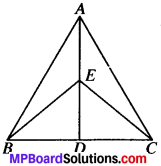
Solution:
Given
E is the mid point of – median AD of ∆ABC.
To prove:
ar (BED) = \(\frac{1}{4}\) ar (ABC)
Proof:
In ∆ABC, AD is the media
ar (ABD) = \(\frac{1}{2}\) ar (ABC) …..(1)
In ∆ABD, BE is the median
ar (BED) = \(\frac{1}{2}\) ar (ABD)
= \(\frac{1}{2}\) [\(\frac{1}{2}\) ar (ABC)]
= \(\frac{1}{4}\) ar (ABC)
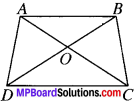
Question 3.
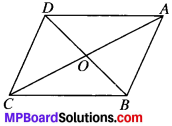
Show that the diagonals of parallelogram divide it into four triangles of equal area.
Solution:
Given.
ABCD is a parallelogram.
To prove:
ar (AOB) = ar (BOC) = ar (COD) = ar (AOD)
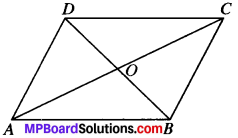
Proof:
In ∆ABC, OA is the median
∴ ar (AOB) = ar (AOD) …..(1)
In AABC, BO is the median
∴ ar (AOB) = ar (BOC) …..(2)
In ABCD, CO is the median
ar (BOC) = ar (COD) …(3)
From (1), (2) and (3), we get
ar (AOB) ar (BOC) = ar (COD) = ar (AOD)
Question 4.
In Fig. given below, ABC and ABC are two triangles on the same base AB. If line – segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).
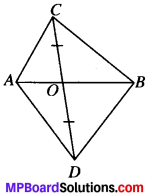
Solution:
Given.
∆ABC and ∆ABD have a common base AB.
OC = OD
To prove
ar (ABC) = ar (ABD)
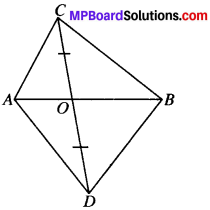
Proof:
As OC = OD,
O is the mid-point of CD
In ∆ACD, O is the median
ar (AOC) = ar(AOD)
In ABCD, BO is the median
ar (BOC) = ar (BOD)
Adding (1) and (2), we get
ar (AOC) + (BOC) = ar (AOD) + ar (BOD)
ar (ABC) = ar (ABC)
![]()
Question 5.
D, E and F are respectively the mid-points of the sides BC, CA and AB of a AABC. Show that
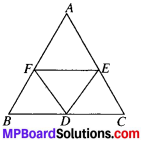
- BDEF is a parallelogram.
- ar (DEF) = \(\frac{1}{2}\) ar (ABC)
- ar (BDEF) = \(\frac{1}{4}\) ar (ABC).
Solution:
D, E, F are the mid points of sides BC, CA and AB of ∆ABC.
To prove:
- BDEF is a parallelogram.
- ar (DEF) = \(\frac{1}{4}\) ar (ABC)
- ar (BDEF) = \(\frac{1}{2}\) ar (ABC)
Proof:
In ∆ABC, F is the mid-point of AB, E is the mid point of AC.
∴ FE ∥ BC and FE = – BC (By MPT)
⇒ FE ∥ BD and FE =BD
1. BDEF is a ∥gm
Similarly CDFE and AEDF are ∥gm
In parallelogram BDEF, DF is the diagonal
∴ ax (BDF) = ar (DEF)
[In a ∥gm diagonal divides it into 2∆s of equal areas]
Similarly, In ∥gm CDFE, DE is a diagoilal …(1)
ar (CDE) = (DEF) …(2)
In ∥gm AEDF, FE is a diagonal
ar (AEF) = ar (DEF) …(3)
From (1), (2) and (3), we get
ar (BDF) = ar (CDF) = ar (AEF) = (DEF) …(4)
2. ar (ABC) = ar (AEF) + ar (ADF) + ar (CDE) + ar (DEF)
ar (ABC) = 4 ar (DEF) [Using (4)]
ar (DEF) = \(\frac{1}{4}\) ar (ABC)
3. ar (BDEF) = ar (BDF) + ar (DEF)
ar (BDEF) = 2ar (DEF) [∴ ar (BDF) = ar (DEF)]
= 2 x \(\frac{1}{4}\) ar (ABC) = \(\frac{1}{2}\) ar (ABC)
Question 6.
In the Fig. diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB – CD, then show that:
- ar (DOC) = ar (AOB)
- ar DCB = ar (ACB)
- DA ∥ CB or ABCD is a parallelogram.
[Hint: From D and B, draw perpendiculars to AC.]
Solution:
Given
ABCD is a quadrilateral in which OB = OD and AB = CD.
To prove:
- ar (DOC) = ar (AOB)
- ar (DCB) = ar (ACB)
- DA ∥ CB or ABCD is a ∥gm
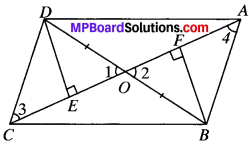
Construction:
Draw DE and BF perpendicular from point D and B on AC.
Proof:
1. In ∆OED and ∆OFB
∠1 = ∠2 (V.O.A.’s)
OD = OB (given)
∠E = ∠F (each 90°)
∆ OED = ∆ OFB (by AAS)
and so DE = BF (by CPCT)
In ∆DEC and ∆BFA, DE = BF (proved)
∠E = ∠F (each 90°)
DC = BA (given)
∆DEC = ∆BFA (by RHS)
and so ∠3 = ∠4 (by CPCT)
ar (OED) = ar (OFB) [∴ AOED = AOFB] …(1)
ar (DEC) = ar (BFB) [∴ ADEC = ABEA] …..(2)
Adding (1) and (2), we get
ar (OED) + ar (DEC) = ar (OFB) = ar (BFA)
ar (OCD) = ar (OAB) …..(3)
2. Adding ar (OBC) on both sides of equation (3)
ar (OCD) + (OBC) = ar (OAB) + ar (OBC)
ar (DCB) = ar (ACB)
3. ∆DCB and ∆ACB have the same base BC and have equal area
∴ they will lie between the same parallels BC and AD
and so BC ∥ AD
∠3 and ∠4 are A.I.A’s and are equal
∴ AB ∥ DC
In quadrilateral ABCD, AB ∥ DC and AB = DC (given)
ABCD is a parallelogram.
![]()
Question 7.
D and E are points on sides AB and AC respectively of ∆ABC such that ar (DBC) = ar (EBQ. Prove that DE ∥ BC.
Solution:
Given
ar (DBC) = ar (EBC)
To prove:
DE ∥ BC
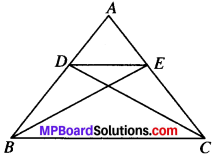
Proof:
∆ DBC and ∆EBC have the same base BC and
ar (DBC) = ar (EBC)
∴ They will lie between the same parallel lines DE and BC.
and so DE ∥ BC
Question 8.
XY is a line parallel to side BC of a triangle ABC. If BE ∥ AC and CF ∥ AB meet XY at E and F respectively, show that ar (ABE) = ar (ACF).
Solution:
Given
XY ∥ BC, BE ∥ AC and CF ∥ AB.
To prove
ar (ABE) = ar (ACF)
Proof:
In quadrilateral ACBE, AE ∥ CB (∴ BC ∥ XY)
and AC ∥ EB
ACBE is a ∥gm
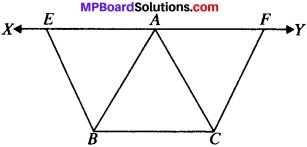
Similarly ABCF is a parallelogram.
∥gm ACBE and ABCF have the same base BC and are between the same parallels BC and AY.
∴ ar (ACBE) = ar (ABCF)
ar (ABE) + ar (ABC) = ar (ABC) + ar (ACF)
∴ ar (ABE) = ar (ACF)
Question 9.
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see Fig. below). Show that ar (ABCD) = ar (PBQR).
[Hint: Joint AC and PQ. Now compare ar (ACQ) and ar (APQ).]
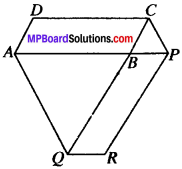
Solution:
Given
ABCD and BPRQ are parallelograms. CP ∥ AQ
To prove:
ar (ABCD) = ar (PBQR)
Construcion:
Join AC and PQ
Proof:
∆ACQ and ∆APQ lie on the same base AQ and are between the same parallels AQ and CP.
∴ ar (ACQ) = ar (APQ)
⇒ ar (ABQ) + ar (ABC) = ar (ABQ) + ar (BQP)
∴ ar (ABC) = ar (BQP) …..(i)
Multiplying (1) by 2 on both sides
2 ar (ABC) = 2 ar (BQP)
∴ ar (ABCD) = ar (PBQR)
[∴ ABCD and PBQR are parallelogram]
![]()
Question 10.
Diagonals AC and BD of a trapezium ABCD with AB ∥ DC intersect each other at C. Prove that ar (AOD) = ar (BOC).
Solution:
Given
ABCD is a trapezium in which AB ∥ DC.
To prove:
ar (AOD) = ar (BOC).
Proof:
∆ADC and ∆BCD lie on the same base DC and between the same parallels AB and CD.
∴ ar (ADC) = ar (BCD)
Subtracting ar (DOC) from both sides
ar (ADC) – ar (DOC) = ar (BCD) – ar (DOC)
ar (AOD) = ar (BOC)
Question 11.
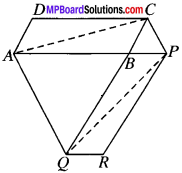
In Fig. ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that:
- ar (ACB) = ar (ACF)
- ar (AEDF) = ar (ABCDE).
Solution:
Given
ABCDE is a pentagon.
To prove:
1. ar (ACB) = ar (ACF)
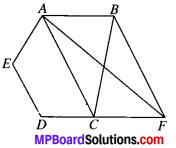
2. ar (AEDF) = ar (ABCDE)
Proof:
∆ACB and ∆ACF lie on the same base AC and between the same parallels AC and BE.
ar (ACB) = ar (ACF)
3. Adding ar (AEDC) on both sides
ar (ACB) + ar (AEDC) = ar (ACF) + ar (AEDC)
ar (ABCDE) = ar (AEDF)
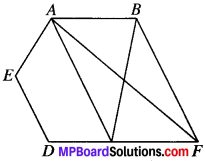
Question 12.
A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Solution:
Given.
ABCD is a quadrilateral.
Construction:
Join AC. Draw DE ∥ CA which intersect BA produced at E.
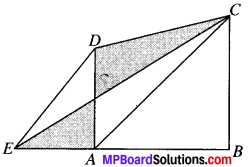
Proof:
∆ADC and ∆ACE both lie on the same base AC and between the same parallels AC and DE.
ar (ADC) = ar (ACE)
Adding ar (ABC) on both sides
ar (ADC) + ar (ABC) = ar (ACE) + ar (ABC)
ar (ABCD) = ar (EBC)
![]()
Question 13.
ABCD is a trapezium with AB ∥ DC. Aline parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY).
[Hint: Join CX.]
Solution:
Given
ABCD is trapezium with AB ∥ DC and AC ∥ XY.
To prove:
ar (ADX) = ar (ACY).
Construction:
Join CX.
Proof:
∆ADX and ∆ACX both lie on the same base AX and between the same parallel AN and DC.
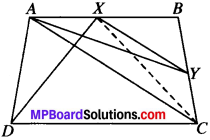
∴ ar (ADX) = ar (ACX) …(1)
∆ACX and ∆ACT both lie on the same base AC and between the same parallels AC and AT.
ar (ADY) = ar (ACX) …(2)
From (1) and (2), we get
ar (ADX) = ar(ACT)
Question 14.
In Fig. below AP ∥ BQ ∥ CR. Prove that ar (AQC) = ar (PBR).
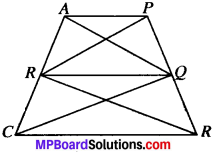
Solution:
Given:
AP∥BQ∥CR.
To prove:
ar (AQC) = ar (PBR)
Proof:
∆ABQ and ∆PBQ both lie on the same base BQ and between the same parallels AP and BQ.
∴ ar (ABQ) = ar (PBQ) …(1)
∆BCQ and ∆BRQ both lie on the same base BQ and between the same parallels BQ and CR.
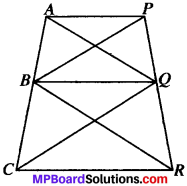
∴ ar (BCQ) = ar (BRQ) …(2)
Adding (1) and (2), we get
ar (ABQ) tar (BCQ) = ar (PBQ) + ar (BRQ)
∴ ar (AQC) = ar (PBR)
Question 15.
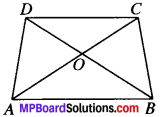
Diagonals AC and BD of a quadrilateral ABCD intersect at 0 in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
Solution:
Given:
ar (AOD) = ar (BOC)
To prove:
ABCD is a trapezium.
Proof:
ar ∠AOD = ar (BOC) (given)
Adding ar (AOB) on both sides
ar (AOD) + ar (AOB) = ar (BOC) + ar (AOB)
ar (ABD) = ar (ABC)
∆ABD and ∆ABC both lie on same base AB and have equal area.
∴ they will lie between the same parallels.
⇒ AB ∥ DC
∴ ABCD is a trapezium.
Question 16.
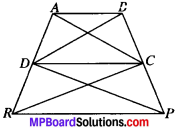
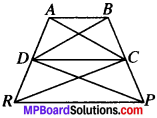
In Fig. below, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
Solution:
Given
ar (DRC) = ar (DPC)
ar (BDP) = ar (ARC)
To prove:
ABCD and DCPR are trapezium.
Proof:
∆DRC and ∆DPC both lie on the same base DC and have equal area .•. They will lie between the same parallels.
⇒ DC ∥ BP
and so DCPR is a trapezium.
ar (BDP) = ar (ARC) [given] …(1)
ar (DPC) = ar (DRC) [given] …(2)
Subtracting (1) and (2), we get
ar (BDP) – ar (DPC) = ar (ARC) – (DRC)
ar (BDC) = ar (ADC)
∆ADC and ∆BDC both lie on same base DC and have equal area.
∴ they will lie between the same parallels
⇒ AB ∥ DC
and so ABCD is a trapezium.