MP Board Class 9th Maths Solutions Chapter 8 चतुर्भुज Additional Questions
MP Board Class 9th Maths Chapter 8 अतिरिक्त परीक्षोपयोगी प्रश्न
MP Board Class 9th Maths Chapter 8 दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
एक समान्तर चतुर्भुज ABCD में AB = 10 cm और ∠AD = 6 cm है। ∠A का समद्विभाजक DC से E पर मिलता है तथा AE और BC बढ़ाने पर F पर मिलते हैं। CF की लम्बाई ज्ञात कीजिए।
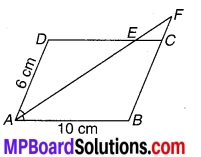
चित्र 8.25
हल:
ABCD एक समानान्तर चतुर्भुज है जिसमें AB = 10 cm AK एवं AD = 6 cm है।
∠A का समद्विभाजक DC को E पर प्रतिच्छेद करता है तथा आगे बढ़ाने पर BC को F पर प्रतिच्छेद करता है।
चूँकि AD || BC को तिर्यक रेखा AB प्रतिच्छेद करती है।
⇒ ∠DAB + ∠ABC = 180° एक ही ओर के अन्त:कोण हैं,
अर्थात् ∠ DAF + ∠ FAB + ∠ABF = 180° ….(1)
एवं ∆ABF में, ∠ FAB + ∠ABF + ∠ BFA = 180° …(2)
⇒ ∠BFA = ∠DAF [समीकरण (1) और (2) से]
अर्थात् ∠BFA = ∠ BAF (∠ DAF = ∠ BAF क्योंकि AF, ∠A का समद्विभाजक है)
⇒ BF = AB (∵ समान कोणों की सम्मुख भुजाएँ हैं)
⇒ BC + CF = AB (चित्रानुसार)
⇒ 6 cm + CF = 10 [AB = 10 cm, BC = AD = 6 cm (दिया है)]
⇒ CF = 10cm – 6 cm = 4 cm
अत: CF का अभीष्ट मान = 4 cm.
प्रश्न 2.
P, Q, R और S क्रमशः चतुर्भुज ABCD की AB, BC, CD R और DA भुजाओं के मध्य-बिन्दु हैं जिसमें AC = BD है। सिद्ध कीजिए कि PQRS एक समचतुर्भुज है।
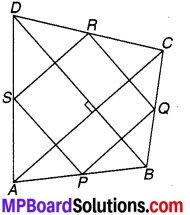
चित्र 8.26
हल:
ABCD एक चतुर्भुज है जिसकी भुजाओं AB, BC, CD और DA के मध्य-बिन्दु क्रमशः PQR और S हैं।
चतुर्भुज के AC = BD.
चूँकि ∆ABC में AB और BC के मध्य-बिन्दु क्रमशः P और Q हैं।
⇒ PQ = \(\frac { 1 }{ 2 }\) AC …(1)
चूँकि ∆ADC में AD और CD के मध्य-बिन्दु क्रमश: S और R हैं।
SR = \(\frac { 1 }{ 2 }\)AC ….(2)
PQ = SR = \(\frac { 1 }{ 2 }\) AC [समीकरण (1) और (2) से] ..(3)
चूँकि ∆BAD में BA और DA के मध्य-बिन्दु क्रमशः P और S है।
⇒ PS = \(\frac { 1 }{ 2 }\)BD …..(4)
चूँकि ∆BCD में BD एवं CD के मध्य-बिन्दु क्रमशः Q और R है
⇒ QR = \(\frac { 1 }{ 2 }\) = BD …..(5)
⇒ PS = QR = \(\frac { 1 }{ 2 }\)BD
PS = QR = \(\frac { 1 }{ 2 }\)AC (चूँकि AC = BD दिया है) ..(6)
⇒ PQ = SR = PS = QR [समीकरण (3) एवं (6) से]
अत: PQRS एक समचतुर्भुज है। इति सिद्धम्
प्रश्न 3.
P, Q, R और S क्रमशः एक चतुर्भुज ABCD की भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं जिसमें AC ⊥ BD है। सिद्ध कीजिए कि PQRS एक आयत है।
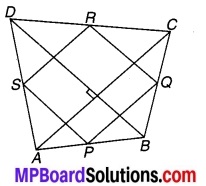
चित्र 8.27
हल:
P, Q, R और S क्रमशः एक चतुर्भुज ABCD की भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं जिसके विकर्ण AC ⊥ BD
चूँकि ∆ABC की भुजाओं AB और BC के मध्य-बिन्दु क्रमशः P और ए हैं।
PQ = \(\frac { 1 }{ 2 }\) = AC एवं PQ || AC …(1)
चूँकि ∆ADC की भुजाओं CD और AD के मध्य-बिन्दु R और S हैं।
⇒ SR = \(\frac { 1 }{ 2 }\) = AC एवं SR || AC …(2)
⇒ PQ = SR एवं PQ || SR [समीकरण (1) और (2) से]
⇒ PQRS एक समान्तर चतुर्भुज है।
चूँकि ∆BAD की भुजाओं BA और DA के मध्य-बिन्दु क्रमशः P और S हैं।
⇒ PS || BD
⇒ चूँकि PQ || AC और PS || BD तथा AC ⊥ BD
⇒ PQ ⊥ PS ∠SPQ = 90° (दो परस्पर लम्ब रेखाओं के समान्तर रेखाएँ परस्पर लम्ब होती हैं)
अत: PORS एक आयत है। (परिभाषा से) इति सिद्धम्
![]()
प्रश्न 4.
ABCD एक आयत है जिसका विकर्ण BD कोण ∠B को समद्विभाजित करता है। दर्शाइए कि ABCD एक वर्ग है।।
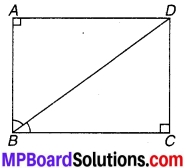
चित्र 8.28
हल:
ABCD एक आयत है जिसका विकर्ण BD, ∠B को समद्विभाजित करता है अर्थात्,
∠ABD = ∠CBD = \(\frac { 1 }{ 2 }\)∠B = \(\frac { 1 }{ 2 }\) x 90° = 45° (आयत का कोण = 90°)
अब ∆BCD में, ∠ BCD + ∠CBD + ∠CDB = 180° (∆ के अन्तः कोण हैं)
⇒ 90° + 45° + ∠CDB = 180° (∠BCD = 90° आयत का कोण तथा ∠CBD = 45°)
⇒ ∠CDB = 45° लेकिन ∠CBD = 45° (सिद्ध कर चुके हैं)
⇒ BC = DC (समान कोणों की सम्मुख भुजाएँ हैं)
⇒ AB = BC = CD = DA
अत: ABCD एक वर्ग है। (परिभाषा से) इति सिद्धम्
MP Board Class 9th Maths Chapter 8 लघु उत्तरीय प्रश्न
प्रश्न 1.
एक चतुर्भुज का एक कोण 108° है तथा अन्य तीनों कोण बराबर हैं। तीनों बराबर कोणों में से प्रत्येक का मान ज्ञात कीजिए।
हल:
माना बराबर कोणों में प्रत्येक का मान = x° है।
⇒ 108° + 3x° = 360° (चतुर्भुज के अन्तः कोण हैं)
⇒ 3x = 360° – 108° = 252°
x = 252/3 = 84°
अतः अभीष्ट बराबर कोणों में से प्रत्येक मान = 84°.
प्रश्न 2.
ABCD एक समलम्ब चतुर्भुज है जिसमें AB || DC और ∠A=∠B = 45°। इस समलम्ब के ∠C और ∠D का मान ज्ञात कीजिए।
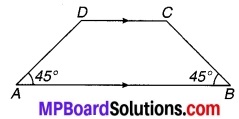
चित्र 8.29
हल:
समलम्ब चतुर्भुज ABCD में AB || DC एवं ∠A = ∠B = 45°
चूँकि AB || DC को तिर्यक रेखा AD काटती है
⇒ ∠A+∠D = 180° (एक ओर के अन्त:कोण हैं)
⇒ 45° + ∠D = 180° (∵∠A = 45°)
⇒ ∠D = 180° – 45° = 135°
चूँकि AB || DC को तिर्यक रेखा BC प्रतिच्छेद करती है।
⇒ ∠B + ∠C = 180° (एक ही ओर के अन्त: कोण है)
⇒ 45° + ∠C = 180° (∠B = 45° दिया है)
⇒ ∠C = 180° – 45° = 135°
अतः अभीष्ट कोणों ∠C और ∠D का प्रत्येक का मान 135° है।
प्रश्न 3.
ABCD एक समचतुर्भुज है जिसमें D से AB पर शीर्षलम्ब AB को समद्विभाजित करता है। समचतुर्भुज के कोण ज्ञात कीजिए।
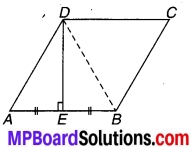
चित्र 8.30
हल:
ABCD एक समचतुर्भुज है जिसमें D से AB पर डाला गया शीर्ष लम्ब DE, AB को समद्विभाजित करता है अर्थात्
AE = EB …(1)
DB को मिलाइए।
चूँकि ∆DAB में आधार AB के मध्य-बिन्दु पर खींचा गया लम्बशीर्ष D से होकर जाता है।
⇒ AD = BD
AB = BC = CD = DA (समचतुर्भुज की भुजाएँ हैं)
⇒ AB = BC = CD = DA = BD (∵ DA = AD = BD)
⇒ ∆ABD एवं ∆BCD समबाहु त्रिभुज है।
⇒ ∠DAB = ∠ BCD = 60° कोण ∠ABC = ∠CDA = 180° – 60° = 120° (क्रमश: ∠DAB एवं ∠BCD के सम्पूरक हैं)
अतः समचतुर्भुज के अभीष्ट कोण ∠A = ∠C = 60° एवं ∠B = ∠D = 120°
![]()
प्रश्न 4.
D, E और F क्रमशः एक समबाहु त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिन्दु mn हैं। दर्शाइए कि ∆DEF भी एक समबाहु त्रिभुज है।
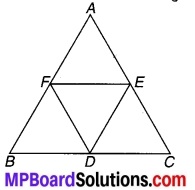
चित्र 8.31
हल:
त्रिभुज ABC में AB = BC = CA तथा D, E और F क्रमशः
BC, CA और AB के मध्य-बिन्दु हैं।
चूँकि ∆ABC में E और F भुजाओं AB और AC के मध्य-बिन्दु हैं।
⇒ EF = \(\frac { 1 }{ 2 }\)BC …(1)
चूँकि ∆ABC में F और D भुजाओं AB और BC के मध्य-बिन्दु हैं।
⇒ FD = \(\frac { 1 }{ 2 }\)CA
चूँकि ∆ABC में D और E भुजाओं BC और CA के मध्य-बिन्दु हैं।
⇒ DE = \(\frac { 1 }{ 2 }\)AB …(3)
⇒ DE = EF = FD (बराबर के आधे बराबर होते हैं)
अतः त्रिभुज DEF की समबाहु त्रिभुज है। इति सिद्धम्
प्रश्न 5.
चतुर्भुज के कोई तीन प्रकार लिखिए, चित्र भी बनाइए। (2019)
हल:
चतुर्भुज के कोई तीन प्रकार
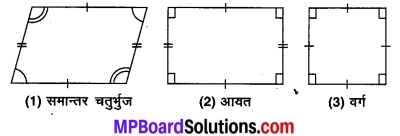
चित्र 8.32
![]()
MP Board Class 9th Maths Chapter 8 अति लघु उत्तरीय प्रश्न
प्रश्न 1.
एक समान्तर चतुर्भुज ABCD के विकर्ण AC और BD परस्पर O बिन्दु पर प्रतिच्छेद करते हैं। यदि OA = 3 cm और OD = 2 cm है, तो AC और BD की लम्बाई ज्ञात कीजिए। उत्तर:
AC = 2OA = 2 x 3 = 6 cm एवं BD = 2 x OD = 2 x 2 = 4 cm, क्योंकि समान्तर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं।
प्रश्न 2.
“समान्तर चतुर्भुज के विकर्ण परस्पर लम्ब होते हैं।” क्या यह कथन सत्य है ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
कथन असत्य है, क्योंकि समान्तर चतुर्भुज के विकर्ण परस्पर किसी भी कोण पर समद्विभाजित करते हैं।
प्रश्न 3.
क्या कोण 110°, 80°, 70° और 95° किसी चतुर्भुज के कोण हो सकते हैं ? क्यों और क्यों नहीं ?
उत्तर:
नहीं हो सकते, क्योंकि कोणों का योग = 110° + 80° + 70° + 95° = 355° है, जबकि चतुर्भुज के चारों कोणों का योग 360° होता है।
प्रश्न 4.
चतुर्भुज ABCD में ∠A+ ∠D = 180° है। इस चतुर्भुज को कौन-सा विशेष नाम दिया जा सकता है ?
उत्तर:
समलम्ब चतुर्भुज, क्योंकि AB || CD है।
प्रश्न 5.
एक चतुर्भुज के सभी कोण बराबर हैं। इस चतुर्भुज को कौन-सा नाम दिया जा सकता है ?
उत्तर:
आयत, क्योंकि आयत का प्रत्येक कोण 90° का होता है।
प्रश्न 6.
एक आयत के विकर्ण परस्पर बराबर और लम्ब हैं। क्या यह कथन सत्य है ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
कथन असत्य है, क्योंकि आयत के विकर्णों का परस्पर लम्ब होना आवश्यक नहीं है।
प्रश्न 7.
क्या किसी चतुर्भुज के सभी कोण अधिक कोण हो सकते हैं ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
नहीं हो सकते, क्योंकि चतुर्भुज चारों अन्तः कोणों का योग 360° होता है।
![]()
प्रश्न 8.
∆ABC में AB = 5 cm, BC = 8 cm और CA = 7 cm है। यदि D और E क्रमशः AB और BC के मध्य-बिन्दु हैं, तो DE की लम्बाई निर्धारित कीजिए।
उत्तर:
DE = \(\frac { 1 }{ 2 }\) AC = \(\frac { 7 }{ 2 }\) = 3.5 cm, क्योंकि किसी त्रिभुज में दो भुजाओं के मध्य-बिन्दु को मिलाने
वाला रेखाखण्ड तीसरी के आधा होता है।
प्रश्न 9.
क्या किसी चतुर्भुज के सभी कोण न्यूनकोण हो सकते हैं ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
नहीं हो सकते, क्योंकि इसके अन्तः कोणों का योग चार समकोण से कम होगा जबकि यह चार समकोण होना चाहिए।
प्रश्न 10.
क्या किसी चतुर्भुज के सभी कोण समकोण हो सकते हैं ? अपने उत्तर के लिए कारण दीजिए।
उत्तर:
हो सकते हैं, क्योंकि इनका योग चार समकोण के बराबर है।
प्रश्न 11.
एक चतुर्भुज ABCD के विकर्ण परस्पर समद्विभाजित करते हैं। यदि ∠A= 35° है तो ∠B निर्धारित कीजिए।
उत्तर:
चूँकि चतुर्भुज एक समान्तर चतुर्भुज है। इसलिए ∠A + ∠B = 180° ⇒∠B = 180° – ∠A = 180° – 35° = 145°
प्रश्न 12.
एक चतुर्भुज ABCD के सम्मुख कोण बराबर हैं। यदि AB = 4 cm है, तो CD निर्धारित कीजिए।
उत्तर:
चतुर्भुज एक समान्तर चतुर्भुज है, इसलिए CD = AB = 4 cm.
प्रश्न 13.
चतुर्भुज के कोई चार प्रकार लिखिए। (2019)
उत्तर:
1. समान्तर चतुर्भुज,
2. समचतुर्भुज,
3. समलम्ब चतुर्भुज,
4. आयत।
![]()
प्रश्न 14.
यदि किसी चतुर्भुज के तीन कोण क्रमश: 90°, 120° व 80° हैं, तो चौथा कोण ज्ञात कीजिए। (2019)
हल:
मान लीजिए कि चौथा कोण x है, और चूँकि चतुर्भुज के चारों अन्तः कोणों का योग 360° होता हैं।
इसलिए, 90° + 120° + 80° + x° = 360°
⇒ 290° + x° = 360°
⇒ x° = 360° – 290° = 70°
अतः अभीष्ट कोण का मान = 70°.
प्रश्न 15.
किसी चतुर्भुज के तीन कोण 110°, 80° एवं 70° है, तो उसका चौथा कोण ज्ञात कीजिए। (2019)
हल:
निर्देशः उपर्युक्त प्रश्न की तरह हल करें।
उत्तर:
अभीष्ट कोण का मान = 100°
MP Board Class 9th Maths Chapter 8 वस्तुनिष्ठ प्रश्न
बहु-विकल्पीय प्रश्न
प्रश्न 1.
एक चतुर्भुज के तीन कोण 75°, 90° और 75° हैं। इसका चौथा कोण है :
(a) 90°
(b) 95°
(c) 105°
(d) 120°.
उत्तर:
(d) 120°
प्रश्न 2.
एक आयत का एक विकर्ण उसकी एक भुजा से 25° पर नत है। इसके विकर्णों के बीच न्यूनकोण
(a) 55°
(b) 50°
(c) 40°
(d) 25°
उत्तर:
(b) 50°
![]()
प्रश्न 3.
ABCD एक सम चतुर्भुज है जिसमें ∠ACB = 40° । तब ∠ADB है :
(a) 40°
(b) 45°
(c) 50°
(d) 60°
उत्तर:
(c) 50°
प्रश्न 4.
यदि चतुर्भुज ABCD के कोणों A, B, C और D का इसी क्रम में लेने पर अनुपात 3 : 7 : 6 : 4 है तो ABCD है एक:
(a) समचतुर्भुज
(b) समान्तर चतुर्भुज
(c) समलम्ब
(d) आयत।
उत्तर:
(c) समलम्ब
प्रश्न 5.
चतुर्भुज के चारों कोणों का योग होता है :
(a) 180°
(b) 90°
(c) 360°
(d) 720°.
उत्तर:
(c) 360°
प्रश्न 6.
यदि किसी चतुर्भुज की सम्मुख भुजाएँ समान हों, तो वह होगा :
(a) समलम्ब
(b) चक्रीय चतुर्भुज
(c) समान्तर चतुर्भुज
(d) आयत।
उत्तर:
(c) समान्तर चतुर्भुज
प्रश्न 7.
समान्तर चतुर्भुज ABCD में कोण बराबर होंगे :
(a) ∠A और B
(b) ∠B और ∠C
(c) ∠A और ∠C
(d) ∠C और ∠D.
उत्तर:
(c) ∠A और ∠C
प्रश्न 8.
एक चतुर्भुज के विकर्ण बराबर तथा परस्पर लम्ब हैं, तो वह चतुर्भुज होगा :
(a) आयत
(b) समान्तर चतुर्भुज
(c) वर्ग
(d) समचतुर्भुज।
उत्तर:
(c) वर्ग
प्रश्न 9.
किस आकृति के विकर्ण एक-दूसरे को समद्विभाजित नहीं करते :
(a) आयत
(b) समान्तर चतुर्भुज
(c) समलम्ब चतुर्भुज
(d) समचतुर्भुज।
उत्तर:
(c) समलम्ब चतुर्भुज
![]()
प्रश्न 10.
समचतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं :
(a) समकोण पर
(b) न्यूनकोण पर
(c) अधिक कोण पर
(d) इनमें से कोई नहीं।
उत्तर:
(a) समकोण पर
प्रश्न 11.
आयत का प्रत्येक कोण होता है :
(a) 90°
(b) 180°
(c) 360°
(d) 270°.
उत्तर:
(a) 90°
प्रश्न 12.
किसी चतुर्भुज के ऐसे दो कोण जिनकी कोई भुजा उभयनिष्ठ न हो, कहलाते हैं :
(a) सम्मुख कोण
(b) आसन्न कोण
(c) समकोण
(d) न्यूनकोण।
उत्तर:
(a) सम्मुख कोण
रिक्त स्थानों की पूर्ति
1. समान्तर चतुर्भुज के दोनों विकर्ण परस्पर ……. करते हैं।
2. आयत के विकर्ण बराबर होते हैं तथा एक-दूसरे को …………. करते हैं।
3. किसी वर्ग की भुजाओं के मध्य-बिन्दुओं को मिलाने से निर्मित चतुर्भुज ……. होगा।
4. यदि किसी समान्तर चतुर्भुज के विकर्ण परस्पर समान और लम्ब हों तो वह चतुर्भुज …….. होगा।
5. वह चतुर्भुज जिसके विकर्ण परस्पर समकोण पर समद्विभाजित करें ……….. होता है।
उत्तर:
1. समद्विभाजित,
2. समद्विभाजित,
3. वर्ग,
4. वर्ग,
5. समचतुर्भुज ।
जोड़ी मिलान

उत्तर:
1. → (c),
2. → (d),
3. → (e),
4. → (a),
5. → (b),
6. → (g),
7. → (f).
![]()
सत्य/असत्य कथन
1. चतुर्भुज के चारों कोणों का योग 180° होता है।
2. समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं।
3. समलम्ब चतुर्भुज की सम्मुख भुजाएँ समान्तर होती हैं।
4. वर्ग के विकर्ण समान होते हैं तथा परस्पर समकोण पर समद्विभाजित करते हैं।
5. यदि किसी समान्तर चतुर्भुज के विकर्ण एक-दूसरे पर लम्ब और बराबर हों, तो वह आयत होता है।
उत्तर:
1. असत्य,
2. सत्य,
3. असत्य,
4. सत्य,
5. असत्य।
एक शब्द/वाक्य में उत्तर
1. चार रेखाखण्डों में निर्मित आकृति क्या कहलाती है?
2. यदि किसी चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर और समान्तर हो तो वह चतुर्भुज क्या होगा?
3. किसी त्रिभुज की दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाली रेखा और तीसरी भुजा में क्या सम्बन्ध
4. किसी त्रिभुज की एक भुजा के मध्य-बिन्दु से दूसरी, भुजा के समान्तर खींची गई रेखा तीसरी भुजा को किस अनुपात में विभक्त करती है?
5. किसी चतुर्भुज में कितने शीर्ष होते हैं?
6. आयत का प्रत्येक कोण कितने अंश का होता है? (2019)
उत्तर:
1. चतुर्भुज,
2. समान्तर चतुर्भुज,
3. तीसरी भुजा के समान्तर और आधी,
4. 1 : 1,
5. चार,
6. 90°.