MP Board Class 9th Maths Solutions Chapter 6 Lines and Angles Ex 6.3
Question 1.
In Fig. given below, sides QP and RQ of ∆PQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ.
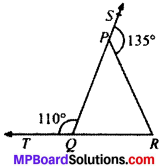
Solution:
Given
∠SPR = 135°
∠PQT = 110°
To find. ∠PRQ
Calculation:
∠Q = 110°
110° + ∠PQR = 180° (LPA’s)
∠1 = 70°
∠P = ∠1 + ∠PRQ
135° = 70° + ∠PRQ
135° – 70° = ∠PRQ
65° = ∠PRQ
Question 2.
In Fig. given below, ∠X = 62°, ∠XYZ = 54°. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ∠XYZ, find ∠OZY and ∠YOZ.
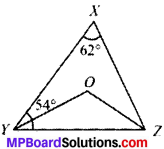
Solution:
Given
∠X = 62°, ∠XYZ = 54°
∠OYZ = \(\frac{1}{2}\)∠XYZ
∠OZY = \(\frac{1}{2}\)∠XZY
To find ∠OZY and ∠YOZ
Calculation:
In ∠XYZ
∠X + ∠Y + ∠Z = 180° (ASP)
62° + 54° + ∠Z = 180°
116° + ∠Z = 180°
∴ ∠Z = 64°
In ∠OYZ
∠OYZ + ∠OZY + ∠O = 180° (ASP)
⇒ \(\frac{1}{2}\)∠XYZ + \(\frac{1}{2}\)∠XZY + ∠O = 180°
32° + 27° + ∠O = 180°
59° + ∠O = 180°
∠O = 121°
Question 3.
In Fig. given below, if AS ∥ DE, ∠BAC = 35° and ∠CDE = 53°, find ∠DCE.
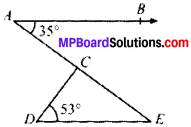
Solution:
Given
AS ∥ DE,
∠BAC = 35°
∠CDE = 53°
To find. ∠DCE
Calculation:
AB ∥ DE and AE is the transversal.
∠BAE = ∠AED = 35°
In ∆DEC
∠D + ∠E + ∠C = 180°
53° + 35° + ∠C = 180°
88° + ∠C = 180°
∠C = 180° – 88° = 92°
![]()
Question 4.
In Fig. given below, if lines PQ and RS intersect at point T, such that ∠PRT = 40°, ∠RPT = 95° and ∠TSQ = 75°, find ∠SQT.
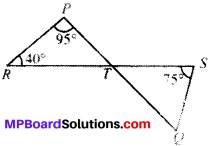
Solution:
Given
∠PRT = 40°
∠RPT = 95°
∠TSQ = 75°
To find. ∠SQT
Calculation:
In ∆PRT
∠P + ∠R + ∠T= 180° (ASP)
95° + 40 ° + ∠T= 180°
∠T = 180° – 135° = 45°
∠T = ∠STQ = 45°
In ∆TSQ
∠STQ + ∠S + ∠Q = 180° (V.O.A’S)
45° + 75° + ∠Q = 180° (ASP)
∠Q = 180° – 120° = 60°
Question 5.
In Fig. given below, if PQ ⊥ PS, PQ ∥ SR, ∠SQR = 28° and ∠QRT = 65°, then find the values of x and y.
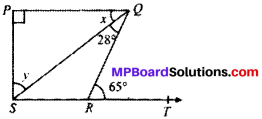
Solution:
Given
PQ ⊥ PS
PQ ∥ SR
∠SQR = 28°
∠QRT = 65°
To find, x and y
Calculation:
PQ ∥ SR and QR is the transversal
x + 28° = 65° (A.I.A’s)
x = 65° – 28° = 37°
In ∆PQS
x + y + 90° = 180° (ASP)
37° + y + 90° = 180°
∴ y = 180° – 127° = 53°
Question 6.
In Fig. given below, the side QR to ∆PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = \(\frac{1}{2}\) ∠QPR.

Solution:
Given
∠TQR = \(\frac{1}{2}\)∠PQR
∠TRS = \(\frac{1}{2}\)∠PRS
To prove. ∠QTR = \(\frac{1}{2}\)∠QPR
Proof:
In ∆PQR
∠PRS = ∠P + ∠Q (EAP)
In ∆TQR, ∠TRS = ∠T + ∠TQR (EAP)
\(\frac{1}{2}\)∠PRS = ∠T + \(\frac{1}{2}\)∠PQR
Multiplying both sides by 2
∠PRS = 2∠T+ ∠PQR
From (1) and (2) we get,
∠P + ∠Q = 2∠T + ∠PQR
∠P=2∠T
∠T= \(\frac{1}{2}\)∠P
∠QTR = \(\frac{1}{2}\)∠QPR
Proved.