MP Board Class 9th Maths Solutions Chapter 6 Lines and Angles Ex 6.1

MP Board Class 9th Maths Solutions Chapter 6 Lines and Angles Ex 6.1

Question 1.
In the given fig., lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.
Solution:
Given
∠AOC + ∠BOE = 70°
∠BOD = 40°
To find:
∠BOE and Reflex ∠COE

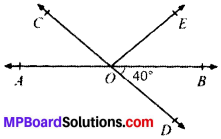
Calculation:
∠BOD
= ∠AOC = 40° (VOA’s)
∠AOC + ∠BOE = 70°
40° + ∠BOE = 70°
∴ ∠BOE = 30°
∠AOC + ∠COE + ∠BOE = 180°
(∴ Angles on the same line)
70° + ∠COE = 180°
∴ ∠COE – 110°
Reflex ∠COE = 360° – ∠COE
= 360° – 110° = 250°

Question 2.
In Fig. below, lines XY and MN intersect at O. If ∠POY = 90° and a : b = 2 : 3, find c.

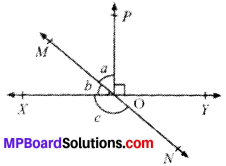
Solution:
Given
∠POY= 90°
a : b = 2 : 3
To find. ∠C
Calculation:
a = 2x
b = 3x
b + a + 90° = 180° (∴ Angles on the same line)
3x + 2x + 90° = 180°
5x = 90°
x = 18°
a = 2 x 18° = 36°
b = 3 x 18° = 54°
b + c = 180 (LPA’s)
c = 180° – 54° = 126°

Question 3.
In Fig. below, if ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.

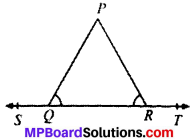
Solution:
Given
∠PQR = ∠PRQ
To prove:
∠PQS = ∠PRT
Proof:
∠PQS + ∠PQR = 180° (LPA’s) …..(1)
∠PRT + ∠PRQ = 180° (LPA’s)
=> ∠PRT + ∠PQR = 180° (∴ ∠PRQ = ∠PQR) …(2)
From (1) and (2), we get
∠PQS + ∠PQR = ∠PRT + ∠PQR
∠PQS = ∠PRT Proved.

Question 4.
In Fig. below, if x + y = w + z, then prove that AOB is a line.

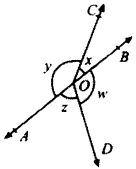
Solution:
Given
x + y = w + z
To prove
AOB is a line
Proof:
x + y + z + w = 360° (Complete angle)
x + y + x + y = 360° (∴ w + z = x + y)
2(x + y) = 360°
x + y = 180° (LPA’s)
AOB is a line. Proved

Question 5.
In Fig. below. POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that
∠ROS = \(\frac{1}{2}\) (∠QOS – ∠POS).
Solution:
Given
POQ is a line, OR ⊥ PQ

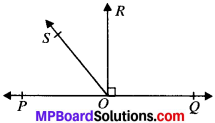
To prove:
∠ROS = \(\frac{1}{2}\) (∠QOS – ∠POS).
Proof:
∠QOS = ∠QOR + ∠ROS
∠QOS = 90° + ∠ROS ….(1)
∠POS = ∠POR – ∠ROS
∠POS = 90° – ∠ROS …..(2)
Subtracting (1) and (2), we get
∠QOS – ∠POS = 90° + ∠ROS – (90° – ∠ROS)
= 90° + ∠ROS – 90° + ∠ROS
∠QOS – ∠POS = 2 ∠ROS
∠ROS = \(\frac{1}{2}\) (∠QOS – ∠POS)

Question 6.
It is given that ∠XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.
Solution:
Given
∠XYZ = 64°
To find:
∠XYQ and Reflex ∠QYP

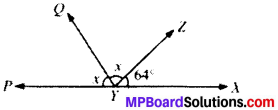
Calculation:
∠XYZ + ∠ZYQ + ∠QYP
= 180° (∴ Angles on the same line)
64° + x + x = 180°
2x = 180° – 64° = 116°
x = 58°
∠XYQ = ∠XYZ + ∠ZYQ
= 64° + 58° = 122°
Reflex ∠QYP = 360° – 58° = 302°

Transversal:
A line which intersects two or more lines at distinct points is called a transversal.

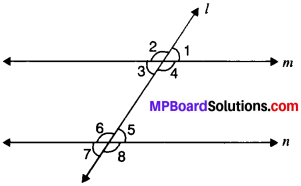
Angles and their Name formed by Transversal:
Line intersects line m and n at point P and Q respectively. So line l is a transversal ftk lines m and n. Observe that four angles are formed at each of the points P and Q. Name these angles ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 and ∠8. There are two type of angles: exterior angles and interior angles as shown in Fig. above.

(a) ∠1, ∠2, ∠7 and ∠8 are Exterior angles and
(b) ∠3, ∠4, ∠5 and ∠6 are Interior angles

Same pairs of angles are formed when a transversal intersects two lines. These are given below:

(a) Corresponding angles:

1. ∠1 and ∠5
2. ∠2 and ∠6
3. ∠4 and ∠8
4. ∠3 and ∠7

(b) Alternate interior angles:

1. ∠4 and ∠6
2. ∠3 and ∠5

(c) Alternate exterior angles:

1. ∠1 and ∠7
2. ∠2 and ∠8

(d) Interior angles on the same side of the transversal:

1. ∠4 and ∠5
2. ∠3 and ∠6

Axiom 3:
If a transversal intersects two parallel lines, then each pair of corresponding angles is equal.

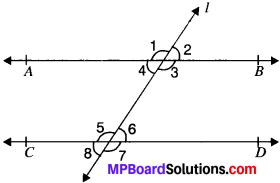
If AB ∥ CD and l is the transversal.
∠1 = ∠5; ∠4 = ∠8
(Corresponding angles)
∠2 = ∠6; ∠3 = ∠7

Axiom 4:
If a transversal intersects two lines such that a pair of correspond-ing angles are equal, then the two lines are parallel to each other.

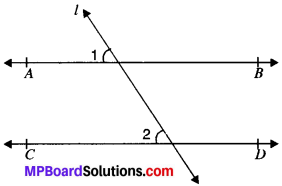
In Fig., AB and CD are two lines, intersected by transversal ‘l’ such that ∠1 = ∠2 (corresponding angles,) then AB ∥ CD.

Theorem 1.
If a transversal intersects two parallel lines, then each pair of alternate interior angles are equal.

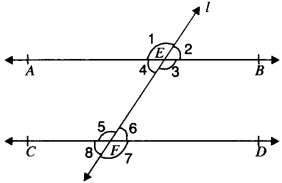
Given. AB ∥ CD and l is the transversal.
To prove:

1. ∠3 = ∠5
2. ∠4 = ∠6

Proof:

∠1 = ∠3 (V.O.A’s) ……(i)
∠1 = ∠5 (Corresponding angle’s) …(ii)
From (i) and (ii), we get
∠3 = ∠5
∠4 = ∠2 (V.O.A’s)
∠2 = ∠6 (Corresponding angle’s)
From (iii) and (iv), we get
∠4 = ∠6. Proved.

Theorem 3.
if a transversal intersect two lines, such that a pair of alternate interior angle is equal, then the two lines are parallel.

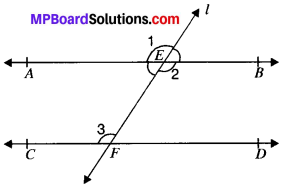
Given
AB and CD are two lines, and l is the transversal.
∠2 = ∠3
To prove:
AB ∥ CD
Proof:
∠2 = ∠3 (V.O.A’s) …..(i)
∠1 = ∠2 (Corresponding angle’s) …(ii)
From (i) and (ii), we get
∠1 = ∠2
∠1 and ∠3 are corresponding angles and are equal.
AB ∥ CD. Proved.

Theorem 4.
If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.

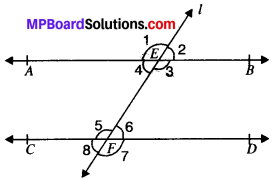
Given
AB ∥ CD and l is the transversal.
To prove:
∠4 + ∠5 = 180° and ∠3 + ∠6 = 180°
Proof
∠3 + ∠4 = 180° (LPA’s) …..(i)
∠3 = ∠5 (AIA’s) …..(ii)
∠4 = ∠6 (AIA’s) …..(iii)
From (i) and (ii) we get
∠5 + ∠4 = 180°
From (i) and (iii), we get
∠3 + ∠6 = 180s.

Theorem 5.
If a transversal intersects two lines, such that a pair of interior angles on the same side of transversal is supplementary, then the two lines are parallel.

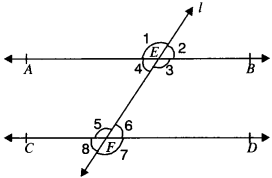
Given
AB and CD are two lines, l is the transversal.
∠4 + ∠5 = 180°
To prove
AB ∥ CD
Proof
∠4 + ∠5 = 180° (Given) …..(i)
∠1 + ∠4 = 180° (LPA’s) …..(ii)
From (i) and (ii), we get
∠4 + ∠5 = ∠1 + ∠4
∠5 = ∠1
∠1 and ∠5 are corresponding angles and are equal.
AB ∥ CD. Proved.

Theorem 6.
Lines which are parallel to the same line are parallel to each other.

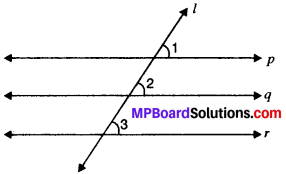
Given, p, q and r are three lines
P ∥ r and q ∥ r
To prove
p ∥ q
Proof
p ∥ r and l is the transversal.
∠1 = ∠3 (Corresponding angles) …..(i)
q ∥ r and l is the transversal.
∠2 = ∠3 (Corresponding angles) …..(ii)
From (i) and (ii), we get
∠1 = ∠2
∠1 and ∠2 are corresponding angles and are equal.
p ∥ q. Proved.

MP Board Class 9th Maths Solutions