MP Board Class 9th Maths Solutions Chapter 2 Polynomials Ex 2.2

by

MP Board Class 9th Maths Solutions Chapter 2 Polynomials Ex 2.2

Question 1.
Find the value of the polynomial 5x – 4x2 + 3 at

  1. x = 0
  2. x = – 1
  3. x = 2.

Solution:
Let f(x) = 5x – 4x2 + 3

1. Value of f(x) at x = 0
= f(0) = 5(0) – 4(0)2 + 3 = 3

2. Value of f(x) at x = – 1
= f(- 1) = 5(- 1) – 4(- 1)2 + 3
= – 5 – 4 + 3 = – 6

3. Value of f(x) at x = 2
= f(2) = 5(2) – 4(2)2 + 3
= 10 – 16 + 3 = – 3.

MP Board Solutions

Question 2.
Find p(0), p(1) and p(2) for each of the following polynomials:

  1. p(y) = y2 – y + 1
  2. p(t) = 2 + t + 2t2 – t3
  3. p(x) = x3
  4. p(x) = (x – 1)(x + 1)

Solution:
1. p(y) = y2 – y + 1
P(0) = (0)2 – (0) + 1
= p(1) = (1)2 – (1) + 1 = 1,
and p(2)2 = (2)2 – (2) + 1
= 4 – 2 + 1 = 3.

2. p(t) = 2 + t + 2t2 – t3
p(0) = 2 + 0 + 2(0)2 – (0)2 = 2
p(1) = 2 + 1 + 2(1)2 – (1)2
= 2 + 1 + 2 – 1 = 4
and p(2) = 2 + 2 + 2(2)2 – (2)3
= 2 + 2 + 8 – 8 = 4

3. p(x) = x3
p(0) = (0)2 = 0,
p(1) = (1)2 = 1,
and p(2) = (2)3 = 8.

4. p(x) = (x – 1) (x + 1)
p(0) = (0 – 1) (0 + 1) = (- 1) (1) = – 1
P(1) = (1 – 1) (1 + 1) = (0) (2) = 0 and
p(2) = (2 – 1) (2 + 1) = (1) (3) = 3

Question 3.
Verify whether the following are zero of the polynomial, written against them.

  1. p(x) = 3x + 1, x = – \(\frac{1}{3}\)
  2. p(x) = 5x – π, x = \(\frac{4}{5}\)
  3. p(x) = x2 -1, x = 1, – 1
  4. p(x) = (x + 1) (x – 2), x – 1, 2
  5. p(x) = x2, x = 0
  6. p(x) = lx + m, x = – \(\frac{m}{l}\)
  7. p(x) = 3x2 – 1, x = – \(\frac{1}{\sqrt{3}}\), \(\frac{2}{\sqrt{3}}\)
  8. p(x) = 2x + 1, x = \(\frac{1}{2}\)

Solution:
1. p(x) = 3x + 1
x = – \(\frac{1}{3}\)
p(- \(\frac{1}{3}\)) = 3(- \(\frac{1}{3}\)) + 1 = 0
= – 3 x \(\frac{1}{3}\) + 1 = – 1 + 1 = 0
As p(- \(\frac{1}{3}\)) = 0, – \(\frac{1}{3}\) is the zero of p(x).

2. p(x) = 5x – π
x = \(\frac{4}{5}\)
p(\(\frac{4}{5}\)) = 5 x \(\frac{4}{5}\) – π = 4 – π
As p(\(\frac{4}{5}\)) ≠ 0,
\(\frac{4}{5}\) is not the zero of p(x).

3 p(x) = x2 – 1, x = 1, -1
P(1) = (1)2 – 1 = 1 – 1 = 0
p(-1) = (-1)2 – 1 = 1 – 1 = 0
As p(1) = 0 and p(-1) = 0
Both 1 and -1 are the zeros of p(x).

4. p(x) = (x + 1)(x – 2)
x = – 1, 2
p(- 1) = (-1 + 1) (- 1 – 2)
= (0) (-3) = 0
p( 2) = (2 + 1) (2 – 2)
= 3 x 0 = 0
As p(- 1) = 0 and p(2) = 0,
Both -1 and 2 are the zeros of p(x).

5. p(x) = x2
x = 0
P(0) = (0)2 = 0
As p(0) = 0, 0 is a zero of p(x)

6. p(x) = lx + m, x = – \(\frac{m}{l}\)
p(- \(\frac{m}{l}\)) = l x – \(\frac{m}{l}\) + m
As p(- \(\frac{m}{l}\)) = 0, (-\(\frac{m}{l}\)) is a zero of p(x).

7.
MP Board Class 9th Maths Solutions Chapter 2 Polynomials Ex 2.2 img-1
8.
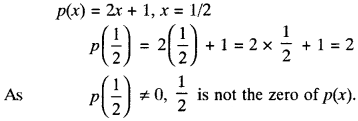
MP Board Class 9th Maths Solutions Chapter 2 Polynomials Ex 2.2 img-2

Question 4.
Find the zero of the polynomial in each of the following cases:

  1. p(x) = x + 5
  2. p(x) = x – 5
  3. p(x) = 2x + 5
  4. p(x) = 3x – 2
  5. p(x) = 3x
  6. p(x) = ax, a ≠ 0
  7. p(x) = cx + d, c ≠ 0, c, d are real numbers.

Solution:
1. p(x) = x + 5
p(x) = 0
x + 5 = 0
x = – 5
∴ – 5 is a zero of the polynomial p(x).

2. P(x) = x – 5
p(x) = 0
x – 5 = 0 x = 5
∴ 5 is a zero of the polynomial p(x).

3. p(x) = 2x + 5
2x + 5 = 0
x = – \(\frac{5}{2}\)
∴ – \(\frac{5}{2}\) is the zero of p(x).

4. p(x) = 3x – 2
3x – 2 = 0
x = \(\frac{2}{3}\)
∴ \(\frac{2}{3}\) is the zero of p(x)

5. p(x) = 3x
3x = 0
x = \(\frac{0}{3}\)
∴ 0 is the zero of p(x).

6. p(x) = ax where a ≠ 0
ax = 0
x = \(\frac{0}{a}\)
∴ 0 is the zero of p(x).

7. p(x) = cx + d where c ≠ 0, c, d are real numbers
cx + d = 0
x = – \(\frac{d}{c}\)
∴ – \(\frac{d}{c}\) is the zero of p(x).

MP Board Solutions

Remainder Theorem:
If a polynomial p{x) is divided by another polynomial (x – a), the remainder isp(a). Where p(x) is any polynomial of degree greater than or equal to one and also degree p(x) > degree p(a) ‘a’ be any real number.

Dividend = divisor x quotient + remainder

Proof:
Let p(x) be any polynomial with degree greater than or equal to 1, suppose that when p(x) is divided by x – a, the quotient is q(x) and remainder is r(x).
p(x) – (x – a) x q(x) + r(x)
p(x) = (x – a) x q(x) + r(x)…..(i)

Case I:
If r(x) = 0
Equation reduce to
p(x) = (x – a) q(x) ……(ii)
On putting x = a, in (ii),
We get p(a) = (a – a) q(a)
p(a) = 0 = Remainder

Case II:
If r(x) ≠ 0
Equation (i) reduced to
p(x) = (x – a) q(x) + r …..(iii)
On putting x = a in (iii), we get
p(a) =(a – a) x q(x) + r
p(a) = r = Remainder
∴ So the remainder is p(a) when p(x) is divided by (x – a).

MP Board Class 9th Maths Solutions