MP Board Class 9th Maths Solutions Chapter 12 Heron’s Formula Ex 12.1

MP Board Class 9th Maths Solutions Chapter 12 Heron’s Formula Ex 12.1

Question 1.
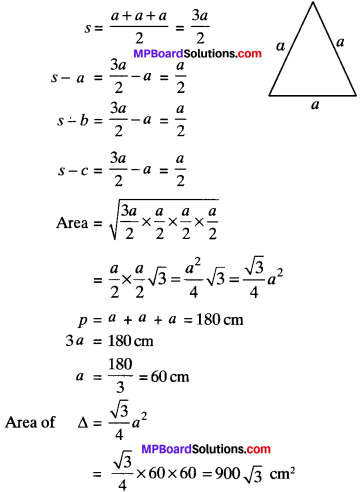
A traffic signal borard, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’ Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?
Solution:

Question 2.
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see Fig.) the advertisements yield an earning of ₹ 5000/m² per year. Acompany hired one of its walls for 3 months. How much rents did it pay?

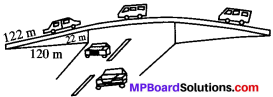
Solution:

s = \(\frac{122+120+22}{2}\) = \(\frac{264}{2}\) = 132 m
s – a = 132 – 122 = 10 m
s – b = 132 – 22 = 12m
s – c = 132 – 22 = 110 m
area of triangular portion of wall = \(\sqrt{32x10x12x110}\)
= \(\sqrt{2x2x3x11x10x2x2x3x11x10}\)
= 10 x 2 x 2 x 3 x 11 = 1320 m²
Rate = ₹ 5000/m² per year
Rent for 3 months = 1320 x \(\frac{5000×3}{12}\)
= 330 x 5000
= ₹ 16,50,000

Question 3.
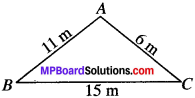
There is a slide in a park. One of its side walls has been painted in some colour with a message “Keep The Park Green And Clean” (see Fig.). If the sides of the wall are 15 m, 11 m and 6 m, find the area painted in colour.

Solution:
a = 15 m
b = 11 m
c = 6m
p = a + b + c
= 15 + 11 + 6
= 32 m P

s = \(\frac{P}{2}\) = \(\frac{32}{2}\) = 16m
s – a = 16 – 15 = 1 m
s – b = 16 – 11 = 5 m
s – c = 16 – 6 = 10m
Area of triangular park = \(\sqrt{16x1x5x10}\)
= \(\sqrt{2x2x2x2x1x5x2x5}\)
= 2 x 2 x 5√2 = 2o\(\sqrt{2m^{2}}\)

Question 4.
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
Solution:

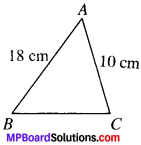
a = 18 cm
b = 10 cm
Let the third side be c
p = 42 cm
18 + 10 + C = 42
C = 14
S = \(\frac{P}{2}\) = \(\frac{42}{2}\) = 21 cm
s – a = 21 – 18 = 3
s – b = 21 – 10 = 11
s – c = 21 – 14 = 7
Area of ∆ = \(\sqrt{21x3x11x7}\) = \(\sqrt{3x7x3x11x7}\)
= 3 x 7\(\sqrt{11}\) = 21\(\sqrt{11}\) cm²

Question 5.
Sides of triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm. Find its area
Solution:
a = 12x
b = 17x
c = 25x
p = 12x + 11x + 25x = 540
54x = 540
x = \(\frac{540}{54}\) = 10
a = 12 x 10 = 120 cm
b = 17 x 10 = 170 cm
c = 25 x 10 = 250 cm
s = \(\frac{P}{2}\) = \(\frac{540}{2}\) = 270 cm
s – a = 270 – 120 = 150 cm
s – b = 270 – 170 = 100 cm
s – c = 270 – 250 = 20 cm
Area of ∆ = \(\sqrt{270x150x100x20}\)
= \(\sqrt{3x3x3x10x3x5x10x10x10x2x10}\)
= 3 x 3 x 10 x 10 x 10
= 9000 cm²

Question 6.
An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
Solution:

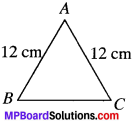
a = 12 cm
b = 12cm
Let the third side be c.
p = a + b + c
30 = 12 + 12 + c
c = 30 – 24 = 6 cm
s = \(\frac{P}{2}\) = \(\frac{30}{2}\) = 15
s – a = 15 – 12 = 3
s – b = 15 – 12 = 3
s – c = 15 – 6 = 9
Area of ∆ = \(\sqrt{5x3x3x9}\)
= \(\sqrt{5x3x3x3x3x3}\)
= 3 x 3\(\sqrt{15}\) = 9\(\sqrt{15}\) cm²

Area of Quadrilaterals:
To find the area of quadrilaterals divide the quadrilateral into two triangles using a diagonal and then use heron’s formula.

Example 1:
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 13 cm, 14 cm and 15 cm and the parallelogram stands on the base 14 cm, And the height of the parallelogram.
Solution:

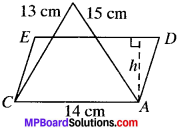
Here, a = 13 cm,
b = 14 cm,
c = 15 cm
Base of parallelogram =14 cm.

= 7 x 3 x 2 x 2
= 84 cm²
Let h be the height of the parallelogram ADEC.
Area of parallelogram ADEC = Area of ∆ABC (given)
Base x height = 84
14 x height = 84
h = \(\frac{84}{14}\)
= 6 cm.

Example 2:
The sides of a quadrilateral, taken in order are 5, 12, 14 and 15 meters respectively, and the angle contained by the first two sides is a right angle. Find its area.
Solution:

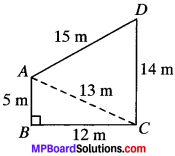
Here, AB = 5m
BC = 12m
CD = 14m
DA = 15 m
Join AC. The ABCD is divided into two triangles ABC and ACD. The area of the quadrilateral is equal to sum of areas of ∆ABC and ∆ADC.
In ∆ABC

area of ABCD
= ar (∆ABC) + ar (∆ACD) –
= (84 + 30)m² = 114m²

Example 3:
In a parallelogram measure of adjacent sides are 34 cm and 20 cm. One of the diagonals is 42 cm. Find the area of the parallelogram.
Solution: In Fig.

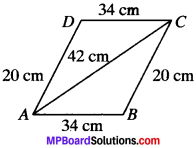
AB = DC = 34 cm
AD = BC = 20 cm
AC =42 cm.
We know that the diagonal of a parallelogram divides it into two tri¬angles of equal area.
∴ Area of parallelogram ABCD = 2 x Area of (∆ABC)
Consider ∆ABC
a = 34cm
b = 20cm
c = 42cm
s = \(\frac{a+b+c}{2}\)
= \(\frac{34+20+42}{2}\)
= \(\frac{96}{2}\) = 48 cm
s – a = 48 – 34 = 14 cm
s – b = 48 – 20 = 28 cm
s – c = 48 – 42 = 6 cm
By Heron’s formula,

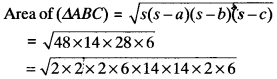
= 2 x 2 x 6 x 14
= 336 cm²
∴ Area of (∥^gm ABCD) = 2 x 336
= 672 cm²

Example 4:
A rhombus sheet, whose perimeter is 32 m and whose one diagonal is 10 m long, is painted on both sides at the rate of? 5 per m2. Find the cost of painting.
Solution:

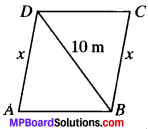
Given P = 32m
BD = 10m
Rate of painting = ₹ 5/m²
Let the sides of rhombus be x m.
P = Ax
⇒ 32 = 4x
∴ x = 8m
So, AB = BC = CD = DA = 8 m
We know that the diagonal of a rhombus divides it into two triangles of equal area. .
∴ Area of rhombus ABCD = 2 x area of ∆ABD
Consider ∆ABD
a = 8m
b = 8m
c = 10m
S = \(\frac{a+b+c}{2}\) = \(\frac{8+8+10}{2}\)
= 13 m.
s – a = 13 – 8 = 5 m
s – b = 13 – 8 = 5m
s – c = 13 -10 = 3 m
By Heron’s formula,
Area of ∆ABD = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{3x5x5x3}\)
= 5 x \(\sqrt{39}\)
= 5 x 6.24 = 31.2 m²
Area of rhombus ABCD = 2 x 31.2 = 62.4 m²
Area of rhombus to be painted = 2 x area of rhombus (∴ Painting is to be done on both sides)
= 2 x 62.4 = 124.80
Cost of painting = Rate x Area
= 5 x 124.80
= ₹ 624.

Example 5:
Two parallel sides of a trapezium are 60 cm and 77 cm other sides are 25 cm and 26 cm. Find the area of trapezium.
Solution:

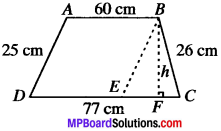
Given AB = 60 cm
DC = 77 cm
AD = 25 cm
BC =26 cm
Draw a line BE ∥ AD from point B.
In ABED
AB ∥ DE
AD ∥ BE
ABED is a parallelogram.
AB = DE = 60
EC = 77 – 60 = 17 cm.
AD = BE = 25 cm
In ∆BEC
a = EC = 17 cm
b = BE = 25 cm
c = BC = 26cm
s = \(\frac{17+25+36}{2}\)
s – a = 34 – 17 = 17 cm
s – b = 34 – 25 = 9 cm
s – c = 34 – 26 = 8cm
By Heron’s formula,

MP Board Class 9th Maths Solutions