MP Board Class 9th Maths Solutions Chapter 11 Constructions Ex 11.1
Question 1.
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Solution:
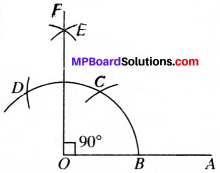
- Draw a ray OA and with O as centre and any radius, draw an arc, cutting OA at B.
- With B as centre and the same radius draw an arc cutting the arc drawn in step (i) at C.
- With C as centre draw another arc with same radius cutting the arc drawn in step (i) at D.
- with C as centre and the same radius draw an arc.
- With D as centre and the same radius draw an arc, cutting the arc drawn in step (iv) at E.
- Draw OE ∴ ∠AOF = 90°
![]()
Question 2.
Construct an angle of 45° at the initial point of a given ray justify the construction.
Solution:
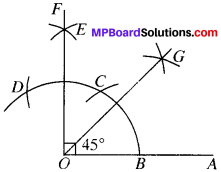
- Draw ∠AOF = 90° by following the same steps for constructing a 90° angle.
- Draw OG, the bisector of ∠AOF.
- ∠AOF= 45°
Question 3.
Construct the angle of the following measurements:
Solution:
- 30°
- 22 \(\frac{1}{2}\)°
- 15°
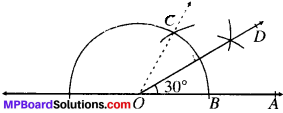
1. 30°
- Draw a ray OA.
- With O as centre and any radius draw an arc which intersect OA at B.
- With B as centre and same radius draw an arc cutting the arc drawn is step (ii) at C.
- Join OC and produce upward
- ∠BOC = 60°
- Draw the bisector OD of ABOC.
- ∠BOD = ∠COD = 30°
2. 22 \(\frac{1}{2}\)°
- Draw a ray OA.
- With O as centre and any radius draw an arc which intersect intersect CM at B.
- With B as centre and same radius draw an arc intersecting the arc drawn in step (ii) at C.
- With C as centre and same radius draw an arc cutting the arc drawn in step (ii) at D.
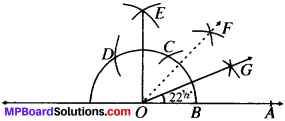
- With C and D as centres and same radius draw arcs to intersect at E.
- Join OE.
- ∠AOG – 90°
- Draw the bisector OE of ∠AOE, to get ∠AOF = 45°
- Draw the bisector OG of ∠AOF.
- ∠AOG = 22\(\frac{1}{2}\)°
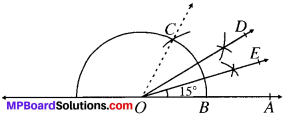
3. 15°
- Draw a ray CM.
- With O as centre and any radius draw an arc which intersect CM at B.
- With B as centre and same radius draw an arc intersecting the arc drawn in step (ii), at C.
- Draw OD as the bisector of ZAOC.
- ∠BOD = 30°
- Draw the bisector OE of ∠AOD.
- ∠AOE = 15°
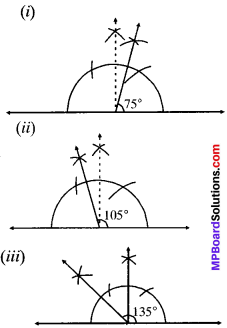
Question 4.
Construct the following angles and verily by measuring them by a protractor.
(i) 75°
(ii) 105°
(iii) 135°
Solution:
Question 5.
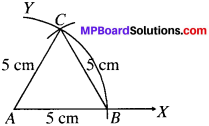
Construct an equilateral triangle given its side and justify the construction.
Solution:
- Draw a ray AY with intial point A.
- With centred and radius equal to length of a side of the A draw an arc BY, cutting the ray AX at B.
- With centre B and the same radius draw an arc cutting are BY at C.
- Join AC and BC to obtain the required A.
Construction of Triangles:
Example 1:
Construction of a Triangle when its base, a base angle and sum of other two sides are given
Solution:
Step of Construction:
- Draw the base PQ.
- At point P draw an angle, MPQ equal to the given angle.
- Cut a line segment PM equal to sum of sides i.e., (PR + RQ) from point P.
- Join MQ.
- Draw the perpendicular bisector of MQ which intersect PM at R.
- Join QR. PQR is the required triangle.
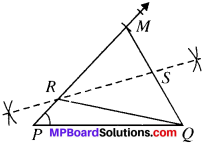
Justification:
Mark points S as shown in Fig.
QS = MS (∴ RS is the perpendicular bisector of MQ)
RS = RS (Common)
∠QSR = ∠MSR (Each \({ 90 }^{ \underline { 0 } }\))
∆RSQ ≅ ∆RSQ (By SAS)
and so PQ = RM (By CPCT)
Now PR = PM – RM = PM – RQ
PM = PR + RQ.
![]()
Example 2:
Construct a AABC in which BC = 3.6 cm, AB + AC = 4.8 and A RSM QS – MS RS = RS cm and B = ∠60°.
Solution:
Steps of Construction:
- Draw BC = 3.6 cm.
- Draw ∠CBX= \({ 60 }^{ \underline { 0 } }\) at B.
- From BX, cut off line segment BD = 4.8 cm.
- Join DC.
- Draw the perpcndicub: bisector ofDC meeting BD at A.
- joinAC.
- ABC is the required Mangle.
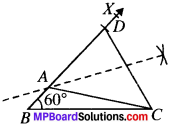
Justification:
‘A‘ lies on the perpendicular bisector of DC
∴ AD = AC
Now BD = 4.8 cm
⇒ BA + AD = 4.8
BA + AC = 4.8 (∴ AD = AC)
Example 3:
Construction of a Triangle when its Base Angle and the Difference of the other two sides are given.
Solution:
Case I:
Given the base BC, a base angle, say ∠B and AB – AC. Steps of Construction:
- Draw the base BC.
- At point B draw an angle ∠CBX equal to the given angle.
- Cut a line segment BD = AB – AC from point B.
- Join DC.
- Draw the perpendicular bisector of . DC which intersect BX at A.
- Join AC.
- ΔABC is the required triangle.
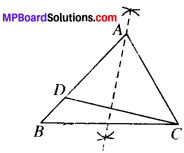
Justification:
As point A lies on the perpendicular bisector of DC
∴ AD = AC
BD = AB – AD = AB – AC (∴ AD = AC)
Case II:
Given the base BC, a base angle say ∠B and (AC – AB).
Steps of Construction:
- Draw the base SC.
- At point S, draw an angle, ∠CBX equal to the given angle and extend the arm XB backward.
- Cut a line segment BD equal to (AC – AB) from the extended arm.
- Join DC.
- Draw the perpendicular bisector of DC which intersect BX at A.
- Join AC.
- ΔABC is the required triangle.
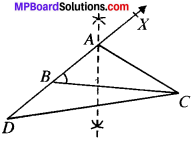
Justification:
As the perpendicular bisector of DC passes through A.
∴ AD – AC
BD = AD – AB
∴ BD = AC – AB
Example 4:
Construct a ∆ABC in which BC = 3.4 cm, AB – AC = 1.5 cm and ∠B = \({ 45 }^{ \underline { 0 } }\).
Solution:
Steps of Construction:
- Draw base BC = 3.4 cm.
- Draw ∠CBX = \({ 45 }^{ \underline { 0 } }\).
- From BX, cut line segment BD =1.5 cm.
- Join DC.
- Draw the perpendicular bisector of DC which intersect BX at A.
- Join AC.
- ABC is the required triangle.
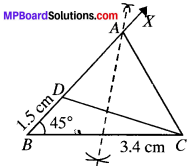
Justification:
As A lies on perpendicular bisector of DC.
AD = AC
BD = 1.5 cm
⇒ AB – AD =1.5 cm
AB – AC =1.5 cm
![]()
Example 5:
Construct a ∆PQR in which QR = 5.8 cm, PR – PQ = 1.8 cm and ∠Q = \({ 45 }^{ \underline { 0 } }\). Justify your construction.
Solution:
Steps of Construction:
- Draw base QR = 5.8 cm.
- Draw ∠RQP = \({ 45 }^{ \underline { 0 } }\).
- Produce arm XQ backward and cut a line segment QS = 1.8 cm.
- Join SR.
- bisector of SR which intersect QX at P.
- Join PR.
- PQR is the required triangle.
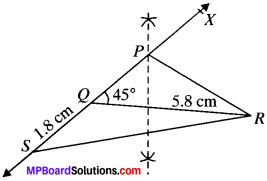
Justification:
As P lies on perpendicular bisector of SR
PS = PR
QS = 1.8 cm
⇒ PS – PQ = 1.8 cm
∴ PR – PQ = 1.8 cm
Example 6:
Construct a ∆ABC in which BC = 5.8 cm, ∠C = \({ 60 }^{ \underline { 0 } }\) and AB – AC = 2.5 cm.
Solution:
Steps of Construction:
- Draw base BC = 5.8 cm
- Draw ∠ACB = \({ 60 }^{ \underline { 0 } }\)
- Produce arm CX backward and cut a line segment CD = 2.5 cm.
- Join BD.
- Draw perpendicular bisector of BD which intersect CX at A.
- Join AB.
- ABC is the required triangle.
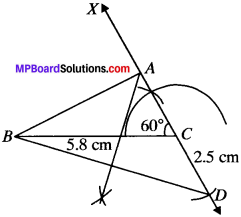
Justification:
A lies on the perpendicular bisector of BD.
∴ AB =AD
CD = 2.5 cm
⇒ AD – AC = 2.5 cm
⇒ AB – AC = 2.5 cm
Example 7:
Construct a ∆ABC in which AC – AB = 3.5 cm, BC = 6.2 cm and ∠C = \({ 45 }^{ \underline { 0 } }\).
Solution:
Steps of Construction:
- Draw BC = 6.2 cm
- Draw ∠ACB = \({ 45 }^{ \underline { 0 } }\)
- Cut CD = 3.5 cm from CX.
- Join BD and draw the perpendicular bisector of BD which intersect CX at A.
- Join AB.
- ABC is the required triangle.
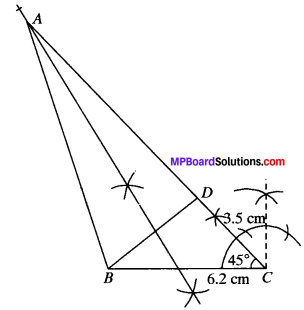
Justification:
As A lies on the perpendicular bisector of BD.
∴ AB = AD
CD = 3.5 cm
⇒ AC – AD = 3.5 cm
∴ AC – AB = 3.5 cm
Example 8:
Construction of a Triangle when its Perimeter and Two Base Angles are given.
Solution:
Given the base angles, ∠B and ∠C and perimeter, i.e., AB + BC + AC.
Steps of Construction:
- Draw a line segment, DE equal to AB + BC + CA.
- Draw ∠EDM and ∠DEN equal to the base angles ∠B and ∠C respectively.
- Draw bisectors of ∠MDE and ∠NED which intersect at A.
- Draw the perpendicular bisectors of AD and AE which intersect DE at B and C respectively.
- Join AE and AC.
- ABC is the required triangle.
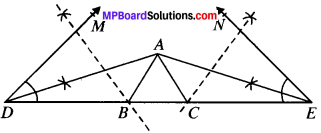
Justification:
As B lies on the perpendicular bisector of AD
∴ AB = DB
In ∆ADB
AB = DB
∠ADB = ∠DAB
(∴ Angles opposite to equal sides of a A are equal)
Similarly, AC = CE
and ∠CAE = ∠CEA
Now DE = DB + BC + CE
= AB + BC + AC
In ∆ABD, ∠ABC = ∠DAB + ∠ADB = ∠ADB + ∠ADB = 2∠ADB
In ∆ACE, ∠ACB = ∠CAE + ∠CEA = ∠CEA + ∠CEA = 2∠CEA
![]()
Example 9:
Construct a triangle whose perimeter is 6.4 cm and angles at the base are \({ 60 }^{ \underline { 0 } }\) and \({ 45 }^{ \underline { 0 } }\).
Solution:
Steps of Construction:
- Draw line segment DE equal to (AB + BC + CA) = 6.4 cm
- Draw ∠EDM = \({ 60 }^{ \underline { 0 } }\) and ∠DEN = \({ 45 }^{ \underline { 0 } }\).
- Draw AD and AE as bisectors of ∠MDE and ∠NED which inter sect at A.
- Draw the perpendicular bisector of AD and AE which intersect DE at B and C respectively.
- Join AB and AC.
- ABC is the required triangle.