MP Board Class 8th Maths Solutions Chapter 4 Practical Geometry Ex 4.3
Question 1.
Construct the following quadrilaterals.
(i) Quadrilateral
MORE
MO = 6 cm
OR = 4.5 cm
∠M = 60°
∠O = 1050°
∠R = 105°
(ii) Quadrilateral
PLAN
PL = 4 cm
LA = 6.5 cm
∠P = 90°
∠A = 6.5 cm
∠N = 85°
![]()
(iii) Parallelogram
HEAR
HE =5 cm
EA = 6 cm
∠B = 85°
(iv) Rectangle
OKAY
OK = 7 cm
KA = 5 cm
Solution:
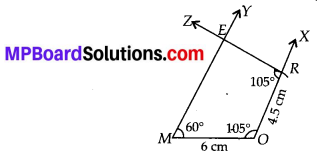
(i) Steps of Construction:
Step-1: Draw MO = 6 cm
Step-2 : Make ∠MOX = 105° and ∠OMY = 60°.
Step-3 : Cut off OR = 4.5 cm on OX.
Step-4 : At point R, draw ∠ORZ = 105° which cuts MY at E.
Hence, MORE is the required quadrilateral.
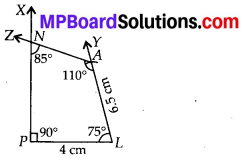
(ii) Here, ∠P = 90°, ∠A = 110°, ∠N = 85°
∴ ∠L = 360° – (∠P + ∠A + ∠N)
= 360° – (90° + 110° + 85°)
= 360°- 285° = 75° ….. (A)
Steps of Construction:
Step-1: Draw PL = 4 cm.
Step-2 : Make ∠LPX = 90° and ∠PLY = 75°. [From (A)]
Step-3 : Cut off LA = 6.5 cm on \(\overrightarrow{L Y}\).
Step-4: Draw ∠LAZ = 110° which cut \(\overrightarrow{P X}\) at point N.
Hence, PLAN is the required quadrilateral.
![]()
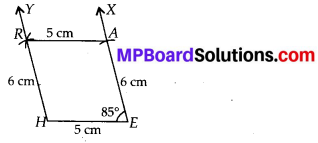
(iii) Since, opposite sides and angles of a parallelogram are equal i.e., ∠R = ∠E = 85°, HE = RA = 5 cm and EA = HR = 6 cm.
Steps of Construction:
Step-1: Draw HE = 5 cm.
Step-2 : Draw ∠HEX = 85°.
Step-3 : Cut off EA = 6 cm on \(\overrightarrow{E X}\)
Step-4: With H as centre and radius equal to 6 cm, draw an arc.
Step-5: With A as centre and radius equal to 5 cm, cut another arc on the arc drawn in step-4 at point R.
Step-6 : Join HR and RA.
Hence HEAR is the required parallelogram.
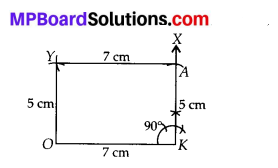
(iv) We know that each of the four angles of a rectangle is equal to 90° and opposite sides are also equal.
OK = YA and KA = OY
Steps of Construction:
Step-1: Draw OK = 7 cm.
Step-2 : Make ∠OKX = 90°.
Step-3 : Cut off KA = 5 cm on \(\overrightarrow{K X}\).
Step-4: With O as centre and radius equal to 5 cm, cut an arc.
Step-5: With A as centre and radius equal to 7 cm cut another arc on the arc drawn in step-4 at point Y.
Step-6 : Join OY and YA.
Hence, OKAY is the required rectangle.