MP Board Class 8th Maths Solutions Chapter 3 चतुर्भुजों को समझना Ex 3.4
प्रश्न 1.
बताइए कथन सत्य है या असत्य –
- सभी आयत वर्ग होते हैं।
- सभी समचतुर्भुज समान्तर चतुर्भुज होते हैं।
- सभी वर्ग समचतुर्भुज और आयत भी होते हैं।
- सभी वर्ग समान्तर चतुर्भुज नहीं होते।
- सभी पतंगें समचतुर्भुज होती हैं।
- सभी समचतुर्भुज पतंग होते हैं।
- सभी समान्तर चतुर्भुज समलम्ब होते हैं।
- सभी वर्ग समलम्ब होते हैं।
उत्तर:
- असत्य
- सत्य
- सत्य
- असत्य
- असत्य
- सत्य
- सत्य
- सत्य।
![]()
प्रश्न 2.
उन सभी चतुर्भुजों की पहचान कीजिए जिनमें –
- चारों भुजाएँ बराबर लम्बाई की हों।
- चार समकोण हों।
उत्तर:
- ऐसे चतुर्भुज जिनकी चारों भुजाएँ समान लम्बाई की हों, वर्ग और समचतुर्भुज हैं।
- चतुर्भुज जिनमें चार समकोण हों-वर्ग और आयत।
प्रश्न 3.
बताइए कैसे एक वर्ग –
- एक चतुर्भुज
- एक समान्तर चतुर्भुज
- एक समचतुर्भुज
- एक आयत है।
उत्तर:
- एक वर्ग में चार भुजाएँ होती हैं; इसलिए यह एक चतुर्भुज है;
- एक वर्ग की सम्मुख भुजाएँ समान्तर होती हैं; इसलिए यह एक समान्तर चतुर्भुज है।
- वर्ग एक ऐसा समान्तर चतुर्भुज होता है जिसकी सभी भुजाएँ बराबर होती हैं; इसलिए यह एक समचतुर्भुज है।
- वर्ग एक ऐसा समान्तर चतुर्भुज होता है; जिसके सभी कोण समकोण होते हैं; इसलिए यह एक आयत है।
प्रश्न 4.
एक चतुर्भुज का नाम बताइए जिसके विकर्ण –
- एक दूसरे को समद्विभाजित करते हैं।
- एक दूसरे पर लम्ब समद्विभाजक हों।
- बराबर हों।
उत्तर:
- एक चतुर्भुज जिसके विकर्ण एक दूसरे को समद्विभाजित करते हैं-समान्तर चतुर्भुज; समचतुर्भुज; वर्ग और आयत।
- एक चतुर्भुज जिसके विकर्ण एक दूसरे पर लम्ब समद्विभाजक होते हैं समचतुर्भुज; वर्ग।
- एक चतुर्भुज जिसके विकर्ण बराबर होते हैं-वर्ग; आयत।
![]()
प्रश्न 5.
बताइए एक आयत उत्तल चतुर्भुज कैसे हैं?
उत्तर:
एक आयत उत्तल चतुर्भुज है क्योंकि –
- इसके प्रत्येक कोण की माप 180° से कम है।
- इसके दोनों विकर्ण अभ्यंतर में होते हैं। अतः आयत उत्तल चतुर्भुज है।
प्रश्न 6.
ABC एक समकोण त्रिभुज है और ‘o’समकोण की सम्मुख भुजा का मध्य बिन्दु है। बताइए कैसे ‘o’ बिन्दु A, B तथा C से समान दूरी पर स्थित है। (बिन्दुओं से चिह्नित अतिरिक्त भुजाएँ आपकी सहायता के लिए खींची गई हैं)।
हल:
BO को D तक इस प्रकार आगे बढ़ाते हैं कि BO = OD.
AD और DC को मिलाया।
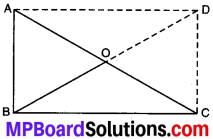
अब ABCD एक आयत है। आयत ABCD में विकर्ण AC और BD बराबर हैं तथा एक-दूसरे को बिन्दु o पर प्रतिच्छेद करते हैं।
\(\overline { AB } \) || \(\overline { BC } \);\(\overline { AB } \) || \(\overline { DC } \)
तथा OA = OC
और OB = OD
परन्तु AC = BD
∴ OA = OB = OC
अतः बिन्दु o; A, B तथा C से समान दूरी पर है।
पाठ्य-पुस्तक पृष्ठ संख्या # 61
सोचिए, चर्चा कीजिए और लिखिए –
प्रश्न 1.
एक राजमिस्त्री एक पत्थर की पट्टी बनाता है। वह इसे आयताकार बनाना चाहता है। कितने अलग-अलग तरीकों से यह विश्वास हो सकता है कि यह आयताकार है?
उत्तर:
राजमिस्त्री को पत्थर की पट्टी को आयताकार बनाने के लिए निम्न प्रकार विश्वास हो सकता है –
- पट्टी की आमने-सामने के किनारे बराबर हों।
- विकर्ण बराबर हों।
- प्रत्येक कोण 90° का हो।
![]()
प्रश्न 2.
वर्ग को आयत के रूप में परिभाषित किया गया था जिसकी सभी भुजाएँ बराबर होती हैं। क्या हम इसे समचतुर्भुज के रूप में परिभाषित कर सकते हैं जिसके कोण बराबर माप के हों? इस विचार को स्पष्ट कीजिए।
उत्तर:
हम वर्ग को समचतुर्भुज के रूप में परिभाषित नहीं कर सकते जब तक कि इसके विकर्ण बराबर नहीं होते और प्रत्येक कोण समकोण नहीं हो।
प्रश्न 3.
क्या एक समलम्ब के सभी कोण बराबर माप के हो सकते हैं? क्या इसकी सभी भुजाएँ बराबर हो सकती हैं? वर्णन कीजिए।
उत्तर:
1. समलम्ब के सभी कोण बराबर माप के हो सकते हैं जबकि सम्मुख भुजाएँ समान्तर हों। लेकिन समलम्ब में भुजा का एक युग्म ही समान्तर होता है।
2. समलम्ब की सभी भुजाएँ बराबर नहीं हो सकती जब तक कि सम्मुख भुजाएँ समान्तर न हो जाएँ। लेकिन समलम्ब एक ऐसा चतुर्भुज है जिसमें भुजाओं का एक युग्म ही समान्तर होता है।