MP Board Class 7th Maths Solutions Chapter 7 त्रिभुजों की सर्वांगसमता Ex 7.2
प्रश्न 1.
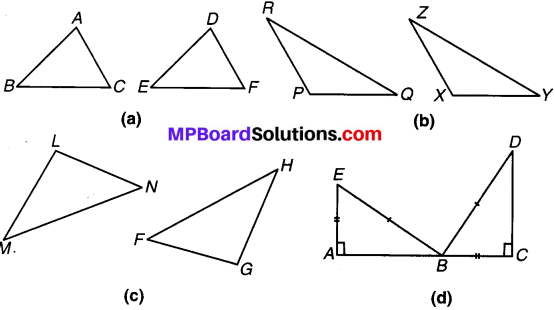
निम्न में आप कौन-से सर्वांगसम प्रतिबन्धों का प्रयोग करेंगे ?
(a) दिया है : AC = DF AB = DE, BC = EF
इसलिए, ∆ABC ≅ ∆DEF
(b) दिया है : ZX = RP RQ = ZY
∠PRQ = ∠XZY
इसलिए, ∆PQR = ∆XYZ
(c) दिया है: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
इसलिए, ∆LMN ≅ ∆GFH
(d) दिया है: EB = DB
AE = BC
∠A = ∠C
इसलिए, ∆ABE ≅ ∆CDB
उत्तर:
(a) S.S.S. सर्वांगसमता प्रतिबन्ध द्वारा,
∆ABC ≅ ∆DEE
(b) S.A.S. सर्वांगसमता प्रतिबन्ध द्वारा,
∆PQR ≅ ∆XYZ.
(c) A.S.A. सर्वांगसमता प्रतिबन्ध द्वारा,
∆LMN ≅ ∆GFH.
(d) R.H.S. सर्वांगसमता प्रतिबन्ध द्वारा,
∆ABE ≅ ∆CDB.
![]()
प्रश्न 2.
आप ∆ART ≅ ∆PEN दर्शाना चाहते हैं।
(a) यदि आप S.S.S. सर्वांगसमता प्रतिबन्ध का प्रयोग करें तो आपको दर्शाने की आवश्यकता है:
(i) AR =
(ii) RT =
(iii) AT =
(b) यदि यह दिया गया है कि ∠T = ∠N और आपको S.A.S. प्रतिबन्ध का प्रयोग करना है, तो आपको आवश्यकता होगी:
(i) RT = और (ii) PN =
(c) यदि यह दिया गया है कि AT = PN और आपको A.S.A. प्रतिबन्ध का प्रयोग करना है, तो आपको आवश्यकता होगी:
(i) ? =
(ii) ? =
हल:
(a) ∆ART ≅ ∆PEN को S.S.S. सर्वांगसमता प्रतिबन्ध द्वारा दर्शाने के लिए दर्शाना होगा –
(i) AR = PE
(ii) RT = EN
(iii) AT = PN
(b) ∴ ∠T = ∠N
∴ (i) RT = EN
(ii) PN = AT
(c) यदि AT = PN और A.S.A. सर्वांगसमता के लिए आवश्यकता होगी –
(i) ∠RAT = ∠EPN
(ii) ∠ATR = ∠PNE
प्रश्न 3.
आपको ∆AMP ≅ ∆AMQ दर्शाना है। निम्न चरणों में, रिक्त कारणों को भरिए:
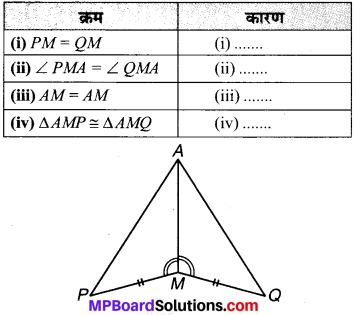
उत्तर:
(i) दिया है
(ii) दिया है
(iii) उभयनिष्ठ
(iv) S.A.S. सर्वांगसमता प्रतिबन्ध।
![]()
प्रश्न 4.
∆ABC में ∠L = 30°, ∠B = 40° और ∠C = 110°, ∆PQR में, ∠P = 30° ∠Q = 40° और ∠R = 110°. एक विद्यार्थी कहता है कि A.A.A. सर्वांगसमता प्रतिबन्ध से ∆ABC ≅ ∆PQR है।
क्या यह कथन सत्य है ? क्यों या क्यों नहीं ?
हल:
यहाँ ∆MBC के तीनों कोण ∆PQR के तीनों कोणों के बराबर हैं। तो यह आवश्यक नहीं कि त्रिभुज सर्वांगसम हों क्योंकि यदि ∆ABC में, भुजा BC = 3.0-सेमी तथा ∆POR में, भुजा QR = 4.0 सेमी हो, तो इस दशा में त्रिभुज के संगत कोण तो बराबर हैं परन्तु यह सर्वांगसम नहीं हैं। क्योंकि BC ≠ QR अतः विद्यार्थी की A.A.A. सर्वांगसमता का प्रतिबन्ध तर्कसंगत नहीं है।
प्रश्न 5.
संलग्न आकृति में दो त्रिभुज ART तथा OWN सर्वांगसम हैं जिनके संगत भागों को अंकित किया गया है। हम लिख सकते हैं ∆RAT = ?
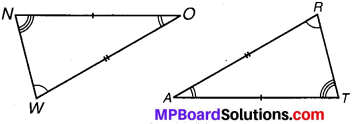
हल:
हम लिख सकते हैं ∆RAT ≅ ∆WON
(∴ O ↔ A, N ↔ T, W ↔ R)
प्रश्न 6.
कथनों को पूरा कीजिए –
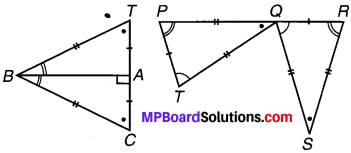
∆BCA ≅ ? ∆QRS ≅ ?
उत्तर:
∆BCA ≅ ∆ABTA, ∆QRS = ∆TPQ
प्रश्न 7.
एक वर्गांकित शीट पर, बराबर क्षेत्रफलों वाले दो त्रिभुजों को इस प्रकार बनाइए कि
(i) त्रिभुज सर्वांगसम हों
(ii) त्रिभुज सर्वांगसम न हों। आप उनके परिमाप के बारे में क्या कह सकते हैं?
हल:
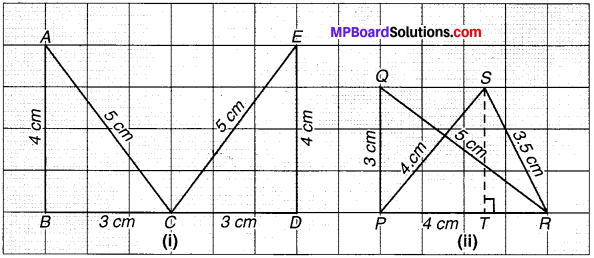
(i) चित्र 7.19 (1) में,
∆ ABC का क्षेत्रफल = ∆EDC का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × 3 × 4 = 6 cm2
∆ ABC का परिमाप = 3 + 4 + 5 = 12 cm
∆ EDE का परिमाप = 3 + 4 + 5 = 12 cm
∆ ABC का परिमाप = ∆EDC का परिमाप,
अतः चित्र 7.19 में, ∆ABC ≅ ∆EDC है।
(ii) चित्र 7.19 (ii) में,
∆ PQR का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × PQ × PR
= \(\frac { 1 }{ 2 } \) × 3 × 4 = 6 cm2
तथा ∆ PSR का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × ST × PR
\(\frac { 1 }{ 2 } \) × 3 × 4 = 6 cm2
∴ ∆ POR का क्षेत्रफल = ∆ PSR का क्षेत्रफल
अब, ∆ PQR का परिमाप = 3 + 4 + 5 = 12 cm
तथा ∆ PRS का परिमाप = 4 + 35 + 4 = 11’5 cm
∆ POR का परिमाप ≠ ∆PRS का परिमाप
अत: चित्र 7.19 (ii) में ∆POR व ∆PRS सर्वांगसम नहीं हैं क्योंकि इनके क्षेत्रफल तो समान हैं परन्तु परिमाप समान नहीं
![]()
प्रश्न 8.
संलग्न आकृति में एक सर्वांगसम भागों का एक अतिरिक्त युग्म बताइए जिससे ∆ABC और ∆PQR सर्वांगसम हो जाएँ। आपने किस प्रतिबन्ध का प्रयोग किया ?
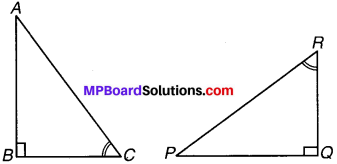
हल:
यहाँ, ∆ABC ≅ ∆PQR
∴ ∠B = ∠Q IR ∠C = ∠R
∴ सर्वांगसम भागों का अतिरिक्त युग्म –
BC = QR
उत्तर हमने यहाँ A.S.A. सर्वांगसम प्रतिबन्ध का प्रयोग किया है।
प्रश्न 9.
चर्चा कीजिए, क्यों?
∆ABC ≅ ∆FED.
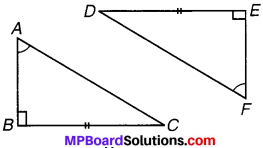
हल:
∠B = ∠E = 90°,
∠A = ∠F (दिया हुआ है)
∴ ∠C = ∠D (तीसरा कोण)
BC = DE (दिया हुआ है)
अत: ASA सर्वांगसम प्रतिबन्ध से ∆ ABC ≅ ∆ FED परिणाम प्राप्त होगा।
पाठ्य-पुस्तक पृष्ठ संख्या # 163
ज्ञानवर्धक क्रियाकलाप
प्रश्न 1.
अलग-अलग माप के वर्गों के कट-आउट सोचिए। अध्यारोपण विधि का प्रयोग वर्गों की सर्वांगसमता के लिए प्रतिबन्ध ज्ञात करने के लिए कीजिए। कैसे “सर्वांगसम भागों” की संकल्पना सर्वांगसम के अंतर्गत उपयोग होती है ? क्या यहाँ संगत भुजाएँ हैं ? क्या यहाँ संगत विकर्ण हैं ?
हल:
हम जानते हैं कि समतल आकृतियाँ सर्वांगसम होती हैं। जब आकृतियों के आकार समान होते हैं तो वे एक-दूसरे की ठीक-ठीक पूरा ढक लेती हैं। सभी वर्ग समान आकृति के होते हैं लेकिन वर्ग का आकार उनकी भुजाओं की लम्बाई पर निर्भर करता है।
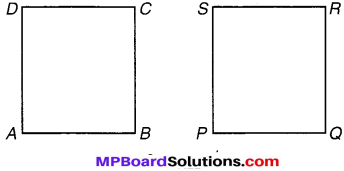
ABCD व PQRS दो वर्ग हैं। वर्ग ABCD के कट-आउट को वर्ग PQRS के ऊपर इस प्रकार रखते हैं कि शीर्ष A, वर्ग PQRS के शीर्ष P पर और भुजा AB भुजा PQ पर आए।
स्पष्ट है कि ABCD वर्ग PQRS को पूर्णतया ढक लेता है।
यदि AB = PQ तो दो वर्ग सर्वागसम होंगे यदि उनकी भुजाओं की लम्बाइयाँ समान हों।
अत: वर्ग ABCD ≅ वर्ग PORS यदि AB = PQ
हम एक वर्ग की किसी भी भुजा को दूसरे वर्ग की किसी भुजा के संगत ले सकते हैं। दूसरी संगत भुजाओं के युग्म इसी प्रकार बदल जाएँगे। यह बात विकर्णों के लिए भी सत्य है।
![]()
प्रश्न 2.
यदि आप वृत्त लेते हैं तो क्या होता है ? दो वृत्तों की सर्वांगसमता के लिए प्रतिबन्ध क्या है ? क्या, आप फिर अध्यारोपण विधि का प्रयोग कर सकते हैं ? पता लगाइए।
हल:
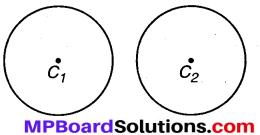
सभी वृत्तों की समान आकृति होती है और वृत्त का आकार वृत्त की त्रिज्या पर निर्भर करता है। यहाँ दो वृत्त C1 व C2 हैं। इनमें से किसी एक वृत्त का कट-आउट (माना वृत्त C2 का) वृत्त C1 पर रखते हैं। वृत्त C2 वृत्त C1 को पूरी तरह ठीक-ठीक ढल लेता है। यदि दोनों वृत्तों की त्रिज्याएँ समान होंगी तो दोनों वृत्त सर्वांगसम होंगे।
वृत्त C1 वृत्त C2 जबकि C1 वृत्त की त्रिज्या = C2 वृत्त की त्रिज्या।
प्रश्न 3.
इस संकल्पना को बढ़ाकर तल की दूसरी आकृतियाँ जैसे समषद्भुज इत्यादि के लिए प्रयत्न कीजिए।
हल:
हम जानते हैं कि समतल आकृतियाँ सर्वांगसम होती हैं यदि वे एक-दूसरे को पूर्णतया ढक लेती हैं। सभी समषट्भुज समान आकृति के होते हैं और इनका आकार समषट्भुज की भुजा की लम्बाई पर निर्भर करता है। दो समषट्भुज ABCDEF व PQRSTU लेते हैं। इनके कट-आउट लेते हैं जिनमें से प्रत्येक की सभी भुजाएँ समान हों।
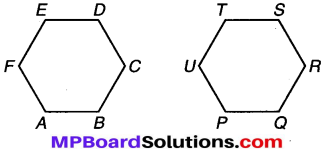
अब PQRSTU के कट-आउट को ABCDEF पर इस प्रकार रखते हैं कि PQRSTU का बिन्दु P बिन्दु A पर आए तथा भुजा PQ भुजा AB पर आए। यदि PQ = AB तो समषट्भुज PQRSTU, समषट्भुज ABCDEF को पूर्णतया ठीक-ठीक ढक लेता है। अत: दो समषट्भुज सर्वांगसम होते हैं यदि इनकी भुजाओं की लम्बाई समान हो।
अत: समषट्भुज ABCDEF = समषट्भुज PQRSTU.
![]()
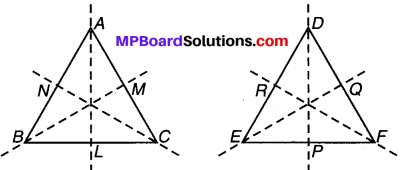
प्रश्न 4.
एक त्रिभुज की दो सर्वांगसम प्रतिलिपियाँ लीजिए। कागज को मोड़कर पता लगाइए कि क्या उनके शीर्ष लम्ब बराबर हैं ? क्या उनकी माध्यिकाएँ समान हैं ? आप उनके परिमाप तथा क्षेत्रफल के बारे में क्या कह सकते हैं ?
हल:
माना ∆ABC ≅ ∆DEF
कागज को मोड़कर प्रत्येक त्रिभुज के शीर्ष बनाए। हम देखते हैं कि
AL = DP BM = EQ और CN = FR
अर्थात् संगत शीर्ष लम्ब समान हैं।
इसी प्रकार हम देख सकते हैं कि सर्वांगसम त्रिभुजों में संगत माध्यिकाएँ समान होती हैं और इनके परिमाप व क्षेत्रफल समान होते हैं।