MP Board Class 7th Maths Solutions Chapter 12 Algebraic Expressions Ex 12.4

MP Board Class 7th Maths Solutions Chapter 12 Algebraic Expressions Ex 12.4

Question 1.
Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the display of electronic
watches or calculators,

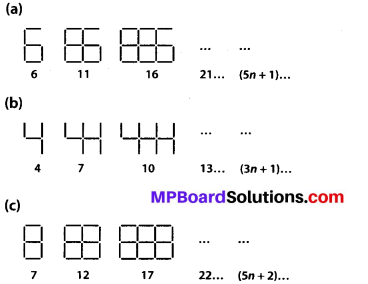
If the number of digits formed is taken to be n, the number of segments required to form n digits is given by the algebraic expression appearing on the right of each pattern. How many segments are required to form 5, 10, 100 digits of the kind

Solution:
(a) It is given that the number of segments required to form n digits of the kind
is (5n + 1).
Number of segments required to form 5 digits = (5 × 5 + 1) = 25 + 1 = 26
Number of segments required to form 10 digits = (5 × 10 + 1) = 50 + 1 = 51
Number of segments required to form 100 digits = (5 × 100 + 1) = 500 + 1 = 501

(b) It is given that the number of segments required to form n digits of the kind
[ is (3n +1).
Number of segments required to form 5 digits = (3 × 5 + 1) = 15 + 1 = 16
Number of segments required to form 10 digits = (3 × 10 + 1) = 30 + 1 = 31
Number of segments required to form 100 digits = (3 × 100 + 1) = 300 + 1 = 301

(c) It is given that the number of segments required to form n digits of the kind
is (5n + 2).
Number of segments required to form 5 digits = (5 × 5 + 2) = 25 + 2 = 27
Number of segments required to form 10 digits = (5 × 10 + 2) = 50 + 2 = 52
Number of segments required to form 100 digits = (5 × 100 + 2) = 500 + 2 = 502

Question 2.
Use the given algebraic expression to complete the table of number patterns.

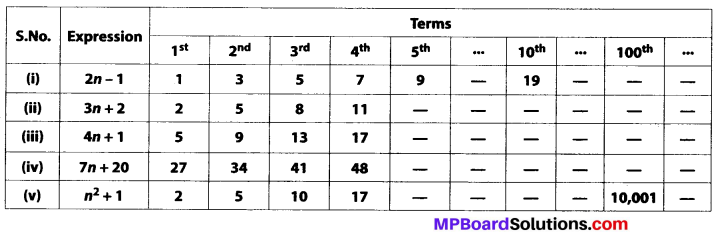
Solution:
(i) Number pattern for expression 2n – 1
Put n = 1, 2, 3,…. and so on, we get

(ii) For expression 3 n + 2, 5^th, 10^th term and 100th term of the pattern are 3 × 5 + 2 = 17, 3 × 10 + 2 = 32 and 3 × 100 + 2 = 302 respectively.
(iii) For expression 4n +1, 5^th, 10^th and 100^th term of the pattern are 4 × 5 +1 = 21, 4 × 10 + 1 = 41 and 4 × 100 + 1 = 401 respectively.
(iv) For expression 7n + 20, 5^th, 10^th and 100^th term of the pattern are 7 × 5 + 1 = 36, 7 × 10 + 20 = 90 and 7 × 100 + 20 = 720 respectively.
(v) For expression n² + 1, 5^th and 10th term of the pattern are 5² + 1 = 26 and 10² + 1 = 101 respectively.

MP Board Class 7th Maths Solutions