MP Board Class 6th Maths Solutions Chapter 5 Understanding Elementary Shapes Ex 5.6
Question 1.
Name the types of following triangles:
(a) Triangle with lengths of sides 7 cm, 8 cm and 9 cm.
(b) ∆ABC with AB = 8.7 cm, AC = 7 cm and BC = 6 cm.
(c) ∆PQR such that PQ = QR – PR = 5 cm.
(d) ∆DEF with m∠D = 90°
(e) ∆XYZ with m∠Y = 90° and XY = YZ.
(f) ∆LMN with m∠L= 30°, m∠M = 70° and m∠N= 80°.
Solution:
(a) Scalene triangle
(b) Scalene triangle
(c) Equilateral triangle
(d) Right-angled triangle
(e) Isosceles right-angled triangle
(f) Acute-angled triangle
![]()
Question 2.
Match the following:


Solution:
(i) ➝ (e);
(ii) ➝ (g);
(iii) ➝ (a);
(iv) ➝ (f);
(v) ➝ (d);
(vi) ➝ (c);
(vii) ➝ (b)
Question 3.
Name each of the following triangles in two different ways: (you may judge the nature of the angle by observation)
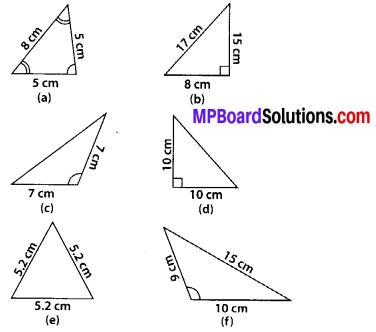
Solution:
(a) Acute angled triangle and Isosceles triangle
(b) Right-angled triangle and Scalene triangle
(c) Obtuse-angled triangle and Isosceles triangle
(d) Right-angled triangle and Isosceles triangle
(e) Acute angled triangle and Equilateral triangle
(f) Obtuse-angled triangle and Scalene triangle
![]()
Question 4.
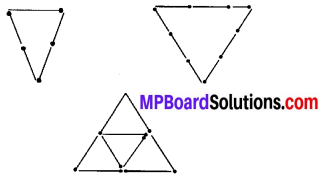
Try to construct triangles using match sticks. Some are shown here.
Can you make a triangle with
(a) 3 matchsticks?
(b) 4 matchsticks?
(c) 5 matchsticks?
(d) 6 matchsticks?
(Remember you have to use all the available matchsticks in each case)
Name the type of triangle in each case.
If you cannot make a triangle, think of reasons for it.
Solution:
(a) Yes, it is possible to make a triangle with 3 matchsticks because sum of lengths of two sides is greater than the length of third side.

(b) No, it is not possible to make a triangle with 4 matchsticks because sum of lengths of two sides is equal to the length of third side.
(c) Yes, it is possible to make a triangle with 5 matchsticks because sum of lengths of two sides is greater than the length of third side.

(d) Yes, it is possible to make a triangle with the help of 6 matchsticks because sum of lengths of two sides is greater than the length of third side.
