In this article, we share MP Board Class 12th Maths Book Solutions Chapter 2 Inverse Trigonometric Functions Ex 2.2 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Solutions Chapter 2 Inverse Trigonometric Functions Ex 2.2
![]()
Question 1.
3sin-1x = sin-1(3x – 4x³). x ∈ [-\(\frac { 1 }{ 2 }\), \(\frac { 1 }{ 2 }\)]
Solution:
Let θ = sin-1 ⇒ x = sin θ
∴ 3x – 4x³ = 3sinθ – 4sin³θ = sin3 θ
∴ 3θ = sin-1(3x – 4x³)
⇒ 3sin-1x = sin-1(3x – 4x³)
Question 2.
3cos-1x = cos-1(4x³ – 3x). x ∈ [\(\frac { 1 }{ 2 }\), 1]
Solution:
Let θ cos-1 ⇒ x = cos θ
4x³ – 3x = 4cos³θ – 3cosθ = cos 3 θ
⇒ 3θ = cos-1(4x³ – 3x)
⇒ 3cos-1x = cos-1(4x³ – 3x)
Question 3.
tan-1\(\frac { 2 }{ 11 }\) + tan-1\(\frac { 7 }{ 24 }\) = tan-1\(\frac { 1 }{ 2 }\)
Solution:
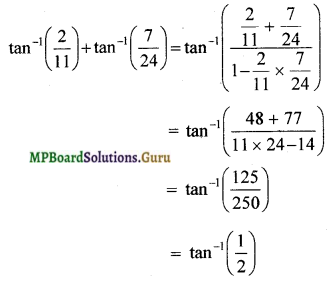
![]()
Question 4.
2tan-1\(\frac { 1 }{ 2 }\) + tan-1\(\frac { 1 }{ 7 }\) = tan-1\(\frac { 31 }{ 17 }\)
Solution:

Question 5.
tan-1\(\frac{\sqrt{1+x^{2}}-1}{x}\), x ≠ 0
Solution:

![]()
Question 6.
tan-1\(\frac{1}{\sqrt{x^{2}-1}}\), |x| > 1
Solution:

Question 7.
tan-1\(\left(\sqrt{\frac{1-\cos x}{1+\cos x}}\right)\), x < π
Solution:

Question 8.
tan-1\(\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)\), x < π
Solution:

Question 9.
tan-1\(\frac{x}{\sqrt{a^{2}-x^{2}}}\), |x| < a
Solution:

![]()
Question 10.
tan-1\(\left(\frac{3 a^{2} x-x^{3}}{a^{3}-3 a x^{2}}\right), a>0 ; \frac{-a}{\sqrt{3}} \leq x \leq \frac{a}{\sqrt{3}}\).
Solution:

Question 11.
tan-1[2 cos(2 sin-1\(\frac{1}{2}\))]
Solution:
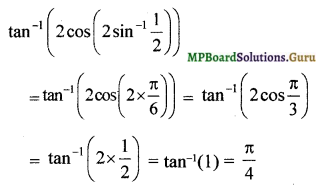
Question 12.
cot(tan-1 a + cot-1 a)
Solution:
Since tan-1 a + cot-1 a = \(\frac{π}{2}\),
cot(tan-1 a + cot-1 a = cot(\(\frac{π}{2}\)) = 0
Question 13.
tan\(\frac{1}{2}\)[\(\left[\sin ^{-1} \frac{2 x}{1+x^{2}}+\cos ^{-1} \frac{1-y^{2}}{1+y^{2}}\right]\))], |x| < 1, y > 0 and xy < 1
Solution:
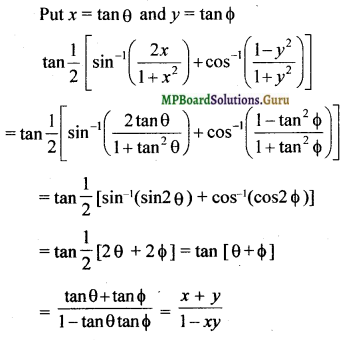
![]()
Question 14.
If sin(sin-1\(\frac{1}{5}\) + cos-1x) = 1, then find the value of x.
Solution:

Question 15.
If tan-1\(\frac{x-1}{x-2}\) + tan-1\(\frac{x+1}{x+2}\), then find the value of x.
Solution:

Question 16.
sin-1\(\left(\sin \frac{2 \pi}{3}\right)\)
Solution:

![]()
Question 17.
tan-1\(\left(\tan \frac{3 \pi}{4}\right)\)
Solution:

Question 18.
tan\(\left(\sin ^{-1} \frac{3}{5}+\cot ^{-1} \frac{3}{2}\right)\)
Solution:

![]()
Question 19.
cos-1\(\left(\cos \frac{7 \pi}{6}\right)\) is equal to
a. \(\frac{7π}{6}\)
b. \(\frac{5π}{6}\)
c. \(\frac{π}{3}\)
d. \(\frac{π}{6}\)
Solution:
b. \(\frac{5π}{6}\)

Question 20.
sin\(\left(\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)\right)\) is equal to
a. \(\frac{1}{2}\)
b. \(\frac{1}{3}\)
c. \(\frac{1}{4}\)
d. 1
Solution:
d. 1
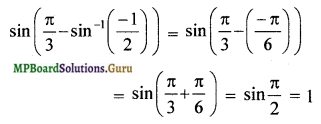
![]()
Question 21.
tan-1\(\sqrt{3}\) – cot-1\(\sqrt{3}\) is equal to
a. π
b. – \(\frac{π}{2}\)
c. 0
d. 2\(\sqrt{3}\)
Solution:
b. – \(\frac{π}{2}\)
tan-1\(\sqrt{3}\) – cot-1(-\(\sqrt{3}\))
= \(\sqrt{3}\) – (π – cot-1\(\sqrt{3}\))
= (tan-1\(\sqrt{3}\) + cot-1\(\sqrt{3}\)) – π
= \(\frac{π}{2}\) – π = – \(\frac{π}{2}\)