MP Board Class 12th Maths Book Solutions Chapter 13 प्रायिकता Ex 13.5

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 13 प्रायिकता Ex 13.5 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 13 प्रायिकता Ex 13.5

प्रश्न 1.
एक पासे को 6 बार उछाला जाता है। यदि ‘पासे पर सम संख्या प्राप्त होना एक सफलता है तो निम्नलिखित की प्रायिकताएँ क्या होंगी?
(i) तथ्यतः 5 सफलताएँ?
(ii) न्यूनतम 5 सफलताएँ?
(iii) अधिकतम 5 सफलताएँ?
हल:
एक पासे पर 3 सम संख्या हैं।
∴ एक पासे पर सम संख्या प्राप्त होने की प्रायिकता

= \(\left(\frac{1}{2}\right)^{6}\) = (6 + 1)
= \(\frac{7}{64}\)
(iii) P (अधिकतम 5 सफलताएँ)
= P(0) + P(1) + P(2) + P(3) + P(4) + P(5)
= [P(O) + P(1) + P(2) + P(3) + P(4) + P(5) + P(6)] – P(6)
= 1 – P(6) =1 – \(\left(\frac{1}{2}\right)^{6}\)
=1 – \(\frac{1}{64}=\frac{63}{64}\)

प्रश्न 2.
पासों के एक जोड़े को 4 बार उछाला जाता है। यदि ‘पासों पर प्राप्त अंकों का दिक होना’ एक सफलता मानी जाती है तो 2 सफलताओं की प्रायिकता ज्ञात कीजिए।
हल:
जब पासे के एक जोड़े को उछाला जाता है, तब n(s) =36
पासों पर प्राप्त अंकों का दिक् प्राप्त होने की प्रायिकता

प्रश्न 3.
वस्तुओं के एक ढेर से 5%त्रुटियुक्त वस्तुएँ हैं। इसकी क्या प्रायिकता है कि 10 वस्तुओं के एक प्रतिदर्श में एक से अधिक त्रुटियुक्त वस्तुएँ नहीं होंगी?
हल:
एक त्रुटियुक्त वस्तु प्राप्त होने की प्रायिकता
= 5% = \(\frac{5}{100}=\frac{1}{20}\)
एक अच्छी वस्तु प्राप्त होने की प्रायिकता
= \(1-\frac{1}{20}=\frac{19}{20}\)
10 वस्तुओं के एक प्रतिदर्श में एक से अधिक त्रुटियुक्त वस्तुएँ नहीं होंगी।

प्रश्न 4.
52 ताश के पत्तों की एक भली-भाँति फेंटी गई गड्डी में से 5 पत्ते उत्तरोतर प्रतिस्थापना सहित निकाले जाते हैं। इनकी क्या प्रायिकता है कि–
(i) सभी 5 पत्ते हुकुम के हों?
(ii) केवल 3 पत्ते हुकुम के हों?
(iii) एक भी पत्ता हुकुम का नहीं हो?
हल:
ताश की गड्डी में कुल पत्तों की संख्या =52
तथा हुकुम के पत्तों की संख्या =13
∴ 1 पत्ता खींचने पर हुकुम का पत्ता आने की प्रायिकता
= \(\frac{13}{52}=\frac{1}{4}\)
∴ हुकुम का पत्ता न आने की प्रायिकता = \(1-\frac{1}{4}=\frac{3}{4}\)
(i) पाँच पत्ते खींचने पर सभी हुकुम के पत्ते आने की | प्रायिकता = \(\left(\frac{1}{4}\right)^{5}=\frac{1}{1024}\)
(ii) पाँच पत्तों में से 3 पत्ते हुकुम के आने की प्रायिकता

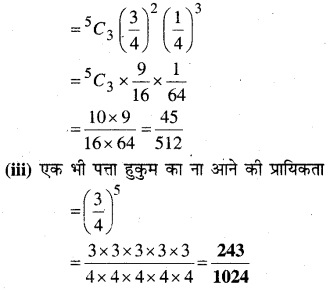
प्रश्न 5.
किसी फैक्टरी में बने एक बल्ब की 150 दिनों के उपयोग के बाद फ्यूज होने की प्रायिकता 0.05 है। इसकी प्रायिकता ज्ञात कीजिए कि इस प्रकार के 5 बल्बों में से
(i) एक भी नहीं
(ii) एक से अधिक नहीं
(iii) एक से अधिक
(iv) कम-से-कम एक, 150 दिनों के उपयोग के बाद फ्यूज हो जाएँगें।
हल:
∵ 150 दिनों के उपयोग होने के बाद फ्यूज की प्रायिकता = 0.05
∴ फ्यूज न होने की प्रायिकता =1 – 0.05 = 0.95
(i) 5 बल्बों में से 150 दिनों के उपयोग होने के बाद फ्यूज न होने की प्रायिकता
= (0.95)⁵ = 0.7738 = 0.77
(ii) एक से अधिक बल्ब फ्यूज नहीं होने की प्रायिकता
= P(0) + P(1)
= (0.95)⁵ + ⁵C₁ x (0.95)⁴ x (0.05)
= (0.95)⁴ (0.95 + 5 x 0.05)
= (0.95)⁴ (0.95 + 0.25)
=(0.95)⁴ x 1.2 = 9.5
(iii) एक से अधिक फ्यूज होने की प्रायिकता
= P(2) + P(3) + P(4) + P(5)
= [P(0) + P(1) + P(2) + P(3) + P(4) + P(5) – P(O) + P(1)]
= 1 – [P(0) + P(1)]
= 1 – (0.95)⁴ x 1.2
= 1 – 0.52 = 0.43
(iv) कम से कम 1 बल्ब फ्यूज होने की प्रायिकता
= P(1) + P(2) + P(3) + P(4) + P(5)
= P(0) + P(1) + P(2) + P(3) + P(4) + P(5) – P(0)
=1 – P(0)
=1 – (0.95)⁵ = 1 – 0.77
= 0.23

प्रश्न 6.
एक थैले में 10 गेंदें हैं जिनमें से प्रत्येक पर 0 से 9 तक के अंकों में से एक अंक लिखा है। यदि थैले से 4 गेंदे उत्तरोत्तर पुन: वापस रखते हुए निकाली जाती हैं तो इसकी क्या प्रायिकता है कि उनमें से किसी भी गेंद पर अंक 0 न लिखा हो?
हल:
एक थैले में 10 गेंदें हैं जिन पर 0 से 9 तक के अंकों में से एक अंक लिखा है।
0 अंक वाली एक गेंद प्राप्त होने की प्रायिकता
= \(\frac{1}{10}\) = 0.1
गेंद पर 0 न लिखा होने की प्रायिकता
= 1 – 0.1 = 0.9
अब 4 गेंदें निकाली गईं।
उनमें से किसी भी गेंद पर अंक 0 न लिखा होने की प्रायिकता
=(0.9)⁴ = \(\left(\frac{9}{10}\right)^{4}\)

प्रश्न 7.
एक सत्य-असत्य प्रकार के 20 प्रश्नों वाली परीक्षा में मान लें कि एक विद्यार्थी एक न्याय्य सिक्के को उछाल कर प्रत्येक प्रश्न का उत्तर निर्धारित करता है। यदि पासे पर चित प्रकट हो तो वह प्रश्न का उत्तर ‘सत्य’ देता है और यदि पट प्रकट हो तो ‘असत्य’ लिखता है। इसकी प्रायिकता ज्ञात कीजिए कि वह कम-से-कम 2 प्रश्नों का सही उत्तर देता है।
हल:
P (सिक्का उछालने पर चित आता है) = \(\frac{1}{2}\)
P (सिक्का उछालने पर चित नहीं आता है)
= \(1-\frac{1}{2}=\frac{1}{2}\)
सत्य उत्तर लिखने की प्रायिकता = \(\frac{1}{2}\)
असत्य उत्तर लिखने की प्रायिकता = \(\frac{1}{2}\)
P (कम-से-कम 2 प्रश्नों के उत्तर सत्य हैं)

प्रश्न 8.
मान लीजिए कि x का बंटन बंटन है। दर्शाइए कि x =3 अधिकतम प्रायिकता वाला परिणाम है।
हल:


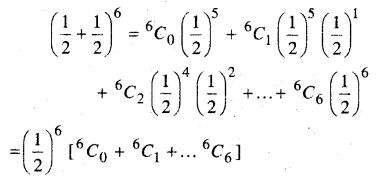
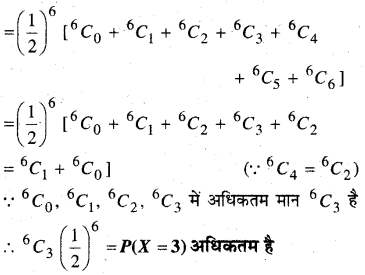
अतः X = 3 पर अधिकतम प्रायिकता वाला परिणाम है।

प्रश्न 9.
एक बहुविकल्पीय परीक्षा में 5 प्रश्न हैं जिनमें प्रत्येक के तीन संभावित उत्तर हैं। इसकी क्या प्रायिकता है कि एक विद्यार्थी केवल अनुमान लगाकर चार या अधिक प्रश्नों का सही उत्तर दे देगा।
हल:
∵ 1 प्रश्न के तीन सम्भावित उत्तर हैं।
∴ सही उत्तर की प्रायिकता = \(\frac{1}{3}\)
P = \(\frac{1}{3}\)
तथा गलत उत्तर देने की प्रायिकता = \(1-\frac{1}{3}=\frac{2}{3}\)
q = \(\frac{2}{3}\)
इसलिए पाँच प्रश्नों में से चार या अधिक सही उत्तरों की प्रायिकता

प्रश्न 10.
एक व्यक्ति एक लॉटरी के 50 टिकट खरीदता है, जिसमें उसके प्रत्येक में जीतने की प्रायिकता है। इसकी क्या प्रायिकता है कि वह
(a) न्यूनतम एक बार
(b) तथ्यतः एक बार
(c) न्यूनतम दो बार, इनाम जीत लेगा।
हल:
1 टिकट पर जीतने की प्रायिकता = \(\frac{1}{100}\)
न जीतने की प्रायिकता = 1 – \(\frac{1}{100}\) = \(\frac{99}{100}\)
(a) ∴ 50 मिनट लेने पर न्यूनतम 1 बार इनाम जीतने की
प्रायिकता = 1 – \(\left(\frac{99}{100}\right)^{50}\)
= 1 – (0.99),sup>50
(b) तथ्यतः एक बार इनाम जीतने की प्रायिकता
= \(^{50} C_{1}\left(\frac{99}{100}\right)^{49}\left(\frac{1}{100}\right)^{1}\)
= \(\frac{1}{2}\left(\frac{99}{100}\right)^{49}\)
(c) न्यूनतम दो बार, इनाम जीतने की प्रायिकता
= P(2) + P(3) +…P(50)
= P(0) + P(1) +…P(50) – [P(0) + P(1)] = 1 – [P(O) + P(1)]
=1 – [P(0) + P(1)]

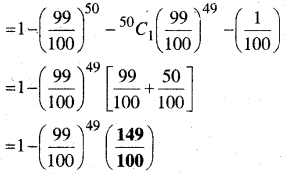
प्रश्न 11.
एक पासे को सात बार उछालने पर तथ्यतः दो बार 5 आने की प्रायिकता ज्ञात कीजिए।
हल:
पासे को 1 बार उछालने पर 5 आने की प्रायिकता = \(\frac{1}{6}\)
तथा 5 न आने की प्रायिकता = \(1-\frac{1}{6}=\frac{5}{6}\)
इसलिए पासे को सात बार उछालने पर दो बार 5 आने की प्रायिकता

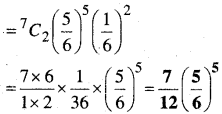
प्रश्न 12.
एक पासे को छः बार उछालने पर अधिकतम 2 बार 6 आने की प्रायिकता ज्ञात कीजिए।
हल:
पासे को 1 बार उछालने पर 6 आने की प्रायिकता = \(\frac{1}{6}\)
तथा 6 न आने की प्रायिकता = \(1-\frac{1}{6}=\frac{5}{6}\)
अत: पासे को 6 बार उछालने पर अधिकतम दो बार 6 आने की प्रायिकता

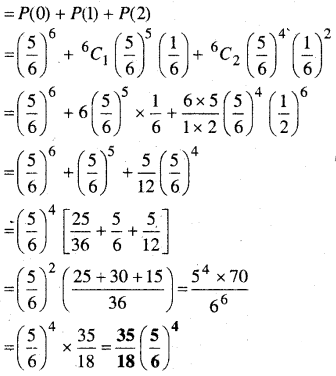
प्रश्न 13.
यह ज्ञात है कि किसी विशेष प्रकार की निर्मित वस्तुओं की संख्या में 10% खराब हैं। इसकी क्या प्रायिकता है कि इस प्रकार की 12 वस्तुओं के यादृच्छिक प्रतिदर्श में से 9 खराब हों?
हल:
निर्मित वस्तुओं में खराब वस्तुओं के चुनने की प्रायिकता
= 10% = \(\frac{1}{10}\)
अच्छी वस्तुओं को चुनने की प्रायिकता
= \(1-\frac{1}{10}=\frac{9}{10}\)
12 वस्तुओं के यादृच्छिक प्रतिदर्श में से 9 खराब होने की प्रायिकता

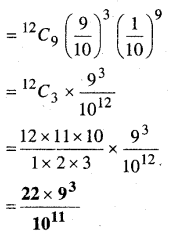
प्रश्न 14.
एक बॉक्स में 100 बल्ब हैं। जिसमें 10 त्रुटियुक्त हैं। 5 बल्ब के नमूने में से, किसी भी बल्ब के त्रुटियुक्त न होने की प्रायिकता है-

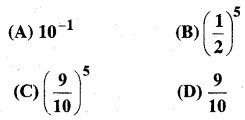
हल:
बॉक्स में बल्बों की संख्या =100
खराब बल्बों की संख्या =10
खराब बल्ब होने की प्रायिकता = \(\frac{10}{100}=\frac{1}{10}\)
अच्छे बल्ब होने की प्रायिकता = \(1-\frac{1}{10}=\frac{9}{10}\)
अतः 5 बल्बों के नमूने में से, किसी भी बल्ब की त्रुटि युक्त न होने की प्रायिकता = \(\left(\frac{9}{10}\right)^{5}\)
अतः विकल्प (C) सही है।

प्रश्न 15.
एक छात्र की तैराक न होने की प्रायिकता है। तब 5 छात्रों में से 4 छात्रों की तैराक होने की प्रायिकता है-

हल: छात्रों की कुल संख्या = 5
एक छात्र की तैराक न होने की प्रायिकता = \(\frac{1}{5}\)
∴ एक छात्र की तैराक होने की प्रायिकता = \(1-\frac{1}{5}=\frac{4}{5}\)
∴ छात्रों का प्रायिकता बंटन जो तैराक है = \(\left(\frac{1}{4}+\frac{4}{5}\right)^{5}\)
इसलिए 5 छात्रों में से 4 छात्रों की तैराक होने की प्रायिकता
= \(^{5} C_{4}\left(\frac{4}{5}\right)^{4} \frac{1}{5}\)
अतः विकल्प (A) सही है।