In this article, we share MP Board Class 12th Maths Book Solutions Chapter 1 संबंध एवं फलन विविध प्रश्नावली Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Book Solutions Chapter 1 संबंध एवं फलन विविध प्रश्नावली
प्रश्न 1.
मान लीजिए कि f: R → R, f(x) = 10x + 7 द्वारा परिभाषित फलन है। एक ऐसा फलन g: R → R ज्ञात कीजिए, जिसके लिए gof = fog = IR हो।
हल:
यहाँ f: R → R इस प्रकार है कि f(x) = 10x + 7
माना y = 10x + 7

अतः f व्युत्क्रमणीय है, जो g : Y → X, g(y) = \(\frac{y – 7}{10}\) से परिभाषित है।
प्रश्न 2.
मान लीजिए कि f: W → W, f(n) = n – 1, यदि ॥ विषम है तथा f (n) = n + 1, यदि n सम है, द्वारा परिभाषित है। सिद्ध कीजिए कि f व्युत्क्रमणीय है। f का प्रतिलोम ज्ञात कीजिए। यहाँ के समस्त पूर्णांकों का समुच्चय
हल:
दिया है : f: W → W को

यदि n1 विषम n2 दोनों सम हों तो
f(n1) = f(n2) ⇒ n1 – 1 = n2 + 1
या n1 – n2 = 2, जो सम्भव नहीं है।
यदि n1 और n2 विषम हों तो
f(n1)= f(n2) ⇒ n1 – 1 = n2 – 1
⇒ n1 = n2
यदि n1 और n2 दोनों सम हों, तो
n1 + 1 = n2 + 1 ⇒ n1 = n2
अतः f एकैकी भी है।
सहप्रान्त में प्रत्येक अवयव 2r + 1, प्रान्त का 2 प्रतिबिम्ब है। इसी प्रकार कोई भी सम संख्या प्रान्त का 2r + 1 का प्रतिबिम्ब है।
इस प्रकार सहप्रान्त का प्रत्येक अवयव प्रान्त के किसी – न – किसी अवयव का प्रतिबिम्ब है।
∴ f आच्छादक तथा व्युत्क्रमणीय है।
अतः f – 1(y) = g(y) इस प्रकार है कि
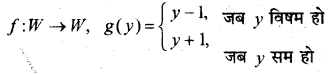
अतः का प्रतिलोम स्वयं है।
प्रश्न 3.
यदि f : R → R जहाँ f(x) = x2 – 3x + 2 द्वारा परिभाषित है तो fIf (x)] ज्ञात कीजिए।
हल:
यहाँ f: R → R, f(x) = x2 – 3x + 2 द्वारा परिभाषित है।
∴ [f(x)] = f(x2 – 3x + 2)
= (x2 – 3x + 2)2 – 3(x2 – 3x + 2) + 2
= (x4 + 9x2 + 4 – 6x3 – 12x + 4x2) + (- 3x2 + 2x – 6) + 2
= x4 – 6x3 + 10x2 – 3x
प्रश्न 4.
सिद्ध कीजिए कि
f: R → {x ϵ R: – 1 < x < 1} जहाँ f(x) = \(\frac{x}{1+|x|}\), x ϵ R द्वारा परिभाषित फलन एकैकी तथा आच्छादक है।
हल:
यहाँ f: R → {x ϵ R : – 1 < x < 1} तथा f(x)= \(\frac{x}{1+|x|}\) द्वारा परिभाषित है।
(a) माना x ≥ 0, |x| = x
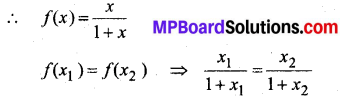
उत्तर
⇒ x1(1 + x2) = x2(1 + x1)
या x1 + x1x2 = x2 + x2x1
जब x < 0 |x| = – x, f(x) = \(\frac{x}{1-x}\)
f(x1) = f(x2) ⇒ \(\frac{x_{1}}{1-x_{1}}=\frac{x_{2}}{1-x_{2}}\)
⇒ x1 (1 – x2) = x2(1 – x1)
⇒ x1 – x1x2 = x2 – x2x1
∴ x1 = x2
अतः f एकैकी है।
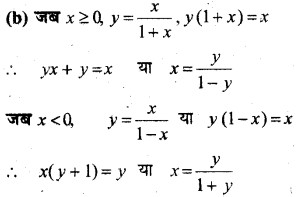
अतः दोनों ही अवस्था में सहप्रान्त का प्रत्येक अवयव प्रान्त के किसी – न – किसी अवयव का प्रतिबिम्ब है।
∴ f आच्छादक है।
अत: f एकैकी तथा आच्छादक है।
![]()
प्रश्न 5.
सिद्ध कीजिए कि f(x) = x3 द्वारा प्रदत्त फलन f: R → R एकैक (Injective) है।
हल:
यहाँ f: R → R, f(x) = x3 द्वारा परिभाषित है।
f(x1) = f(x2) ⇒ x13 x23
⇒ x1 = x1
अतः f एकैकी है।
प्रश्न 6.
दो फलनों f: N → Z तथा g : Z → Z के उदाहरण दीजिए जो इस प्रकार हों कि gof एकैक है परन्तु g एकैक नहीं है।
हल:
(i) यहाँ f: N → Z तथा g: Z → Z द्वारा परिभाषित है।
f(x) = – x, g(x) = |x| से,
g(x)= |x|, – 1, 1 दोनों का प्रतिबिम्ब 1 है। .
∴ g एकैक नहीं है।
परन्तु g[f(x)] =g (- x) = |-x| = |x|
x ϵ N, g[(fx)] = |x|x = x
अतः gof एकैकी है।
(ii) f(x) = -2x, g(x) = |2x|
प्रश्न 7.
दो फलनों f: N → N तथा g: N → N के उदाहरण दीजिए, जो इस प्रकार हों कि gof आच्छादक है किन्तु f आच्छादक नहीं है।
हल:
(i) यहाँ f : N → N तथा g : N → N

f(x) = y = x + 1
∴ x = y – 1
यदि y – 1, x = 0 जो कि प्राकृत संख्या नहीं है।
अतः f आच्छादक नहीं है।
यदि x > 1,
gof (x) = g[f(x)] =g (x + 1) = (x + 1) – 1 = x
अतः gof आच्छादक है।
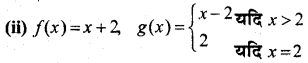
प्रश्न 8.
एक अरिक्त समुच्चय X दिया हुआ है। P(X) जो कि के समस्त उपसमुच्चयों का समुच्चय है, पर विचार कीजिए। ‘निम्नलिखित तरह से P(X) में एक सम्बन्ध R परिभाषित कीजिए-
P(x) में उपसमुच्चयों, A, B के लिए ARB, यदि और केवल यदि A⊂B है। क्या R,P(X) में एक तुल्यता सम्बन्ध है? अपने उत्तर का औचित्य भी लिखिए।
हल:
(i) यहाँ A ⊂ A ⇒ R स्वतुल्य है। .
(ii) A ⊂ B, B ⊄ A ⇒ R सममित नहीं है।
(iii) A ⊂ B, B ⊂ C ⇒ A ⊂ C ⇒ R संक्रामक है।
अतः R तुल्यता सम्बन्ध नहीं है।
प्रश्न 9.
किसी प्रदत्त अरिक्त समुच्चय x के लिए एक द्विआधारी संक्रिया* : P(X) × P(X) → P(X) पर विचार कीजिए, जो A * B = A ∩ B, ∀ A, B ϵ P(X) द्वारा परिभाषित है, जहाँ P(X) समुच्चय x का घात समुच्चय (Power set) है। सिद्ध कीजिए कि इस संक्रिया का तत्समक अवयव X है तथा संक्रिया के लिए P(X) में केवल x व्युत्क्रमणीय अवयव है।
हल:
दिया है : P(X) × P(X) → P(X)
तथा A * B = A ∩ B
∴ X * A = X ∩ A = A, सभी A के लिए
इसी प्रकार A * X = A ∩ X = A.
∴X एक तत्समक अवयव है तथा व्युत्क्रमणीय अवयव है। माना I एक दूसरा तत्समक अवयव है।
∴ I ∩ A = A सभी A के लिए
तथा x ϵ X, I ∩ {x} = {x}
⇒ x ϵ I ⇒ x ⊂ I और I ⊂ x
∴ I = X
![]()
प्रश्न 10.
समुच्चय {1, 2, 3,…., n} से स्वयं तक के समस्त आच्छादक फलनों की संख्या ज्ञात कीजिए।
हल:
माना Y : 1 2 3….n
तथा X : 1 2 3…..n
समुच्चय – Y का प्रत्येक अवयव समुच्चय X में किसी – न – किसी अवयव का प्रतिबिम्ब है।
इस प्रकार x और Y के अवयवों में सम्बन्ध
n (n – 1)(n – 2)… 3 2 1 = n! तरीकों से हो सकता है।
अतः द्विआधारी संक्रियाओं की संख्या n! है।
प्रश्न 11.
मान लीजिए कि S = {a, b, c} तथा T = {1, 2, 3} है। S से T तक के निम्नलिखित फलनों F के लिए F-1 ज्ञात कीजिए, यदि उसका अस्तित्व है :
(i) F = {(1, 3), (b, 2), (c, 1)}
(ii) F = {(a, 2), (b, 1), (c, 1)}
हल:
(i) यहाँ S = {a, b, c},T = {1, 2, 3}
तथा F = {(a, 3), (b, 2), (c, 1)}
F(a)= 3, F(b)= 2, F(c)=1
∴ F-1(3)= a, F-1 (2) = F-1 (1) = c
∴ F-1 = {(3, a),(2, b), (1, c)}
(ii) F = {(a, 2),(b, 1), (c, 1)}
फलन F में b तथा c का प्रतिबिम्ब 1 है।
∴ यह एकैकी नहीं है।
अत: यह फलन व्युत्क्रमणीय नहीं है।
प्रश्न 12.
a * b=|a – b| तथा a o b = a, ∀ a, b ϵ R द्वारा परिभाषित द्विआधारी संक्रियाओं* : R × R → R तथा 0: R × R → R पर विचार कीजिए। सिद्ध कीजिए कि * क्रमविनिमेय है परन्तु साहचर्य नहीं है, . साहचर्य है परन्तु क्रमविनिमेय नहीं है। पुनः सिद्ध कीजिए कि सभी a, b, c ϵ R के लिए a * (b o c) = (a * b) o (a * c) है। [यदि ऐसा होता है तो हम कहते हैं कि संक्रिया * संक्रिया o पर वितरित (Distributes) होती है। क्या o संक्रिया * पर वितरित होती है? अपने उत्तर का औचित्य भी बतलाइए।
हल:
दिया है : a * b = |a – b| और a o b = a
(i) (a) a * b = |a – b|, |b * a| = |b – a| = |a – b|
अतः यह क्रमविनिमेय संक्रिया है।
(b) a * b = |a – b|, b * c = |b – c|
⇒ a * c ≠ |a – c|
अत: यह साहचर्य संक्रिया नहीं है।
(ii) (a) a o b = a, b o a = b ⇒ a ≠ b
अतः o क्रमविनिमेय संक्रिया नहीं है।
a o b = a, b o c = b, a o c = a
अतः o एक साहचर्य संक्रिया है।
(iii) सिद्ध करना है :
a * (boc)= (a * b) 0 (b * c)
L.H.S. = a * (boc)= a * b = |a – b|
R.H.S. = (a * b) 0 (b * c)
= |a – b| o |b – c| = |a – b|
∴ L.H.S. = R..S.
अतः A * (boc)= (a * b) o (b * c)
(iv) क्या a o (b * c) और (a o b) * (a0c) बराबर है?
L.H.S. = a 0 * (b * c) = ao |b – c| = a
R.H.S. = (aob) * (aoc) = a * a = |a – a|= 0
∴ L.H.S. ≠ R.H.S.
अतः संक्रिया o संक्रिया * पर वितरण संक्रिया नहीं है।
![]()
प्रश्न 13.
किसी प्रदत्त अरिक्त समुच्चय x के लिए मान लीजिए कि * : P(X) × P(X) → P(X), जहाँ A * B = (A – B) ∪ (B – A), ∀A, B ϵ P(X) द्वारा परिभाषित है। सिद्ध कीजिए कि रिक्त समुच्चयक ϕ, संक्रिया * का तत्समक है तथा P(X) के समस्त अवयव A व्युत्क्रमणीय हैं, इस प्रकार कि A-1 = A.
हल:
यहाँ * : P(X) × P(X) → P(X) जो इस प्रकार परिभाषित है।
A * B = (A – B) ∪ (B – A)
दिया है : A * B = (A – B) ∪ (B – A)
जब B = ϕ क रखने पर,
A * ϕ = (A – ϕ) ∪ (ϕ – A)
= A ∪ ϕ = A
ϕ * A = (ϕ – A) ∪ (A – ϕ) = ϕ ∪ A = A
⇒ A * ϕ = ϕ * A = A
अतः ϕ तत्समक अवयव है।
(ii) A * A = (A – A) ∪ (A – A) = ϕ
A * A = ϕ = A-1 = A
प्रश्न 14.
निम्नलिखित प्रकार से समुच्चय {0, 1, 2, 3, 4, 5} में एक द्विआधारी संक्रिया * परिभाषित कीजिए।

सिद्ध कीजिए कि शून्य (0) इस संक्रिया का तत्समक है तथा समुच्चय का प्रत्येक अवयव a ≠ 0 व्युत्क्रमणीय है, इस प्रकार कि 6 – c, a का प्रतिलोम है।
हल:
यहाँ संक्रिया समुच्चय A = {0, 1, 2, 3, 4, 5} पर
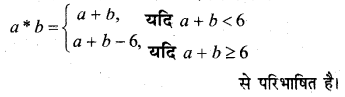
(i) e तत्समक अवयव है, यदि a * e = e * a = a
अब, माना e = 0, a * e = a + 0 = a
e* a = 0 + a = a
∴ a * e = e * a = a
अतः O तत्समक अवयव है।
(ii) b अवयव a का व्युत्क्रम है, यदि a * b = b * a = e
a * (6 – a)= a + (6 – a) – 6 = a + 6 – a – 6 = 0
(6 – a) * a = (6 – a) + a – 6 = 0
∴ a * (6 – a) = (6 – a) * a = 0
अतः A के प्रत्येक अवयव a का 6 – a व्युत्क्रम है।
प्रश्न 15.
मान लीजिए कि A ={ – 1, 0, 1, 2}, B = { – 4, – 2, 0, 2} और f, g: A → B, क्रमशः f(x) = x2 – x, x ϵ A तथा g(x) = 2x\(\left|x-\frac{1}{2}\right|\) – 1. x ϵ A द्वारा परिभाषित फलन हैं क्या है तथा g समान हैं? अपने उत्तर का औचित्य भी बताइए।
हल:
यहाँ, यदि A = { – 1, 0, 1, 2) B = { – 4, – 2, 0, 2}
और f, g . A → B फलन की f(x) = x2 – x, x ϵ A और g(x)= \(\left|x-\frac{1}{2}\right|\) . 1, x ϵ A द्वारा परिभाषित है।

प्रश्न 16.
यदि A = {1, 2, 3} हो तो ऐसे सम्बन्ध जिनमें अवयव (1, 2) तथा (1, 3) हों और जो स्वतुल्य तथा सममित हैं किन्तु संक्रामक नहीं है, की संख्या है
(A) 1
(B) 2
(C) 3
(D) 4
हल:
यहाँ, A = {1, 2, 3}
वह सम्बन्ध जिसमें (1, 2) और (1, 3) हों तथा सम्बन्ध स्वतुल्य व सममित हो तथा संक्रामक न हो,
{(1, 2), (1, 3), (1, 1), (2, 2), (3, 3), (2, 1), (3, 1)}
∴ ऐसा एक ही सम्बन्ध है।
अतः विकल्प (A) सही है।
प्रश्न 17.
यदि A= {1, 2, 3} हो तो अवयव (1, 2) वाले तुल्यता सम्बन्धों की संख्या है
(A) 1
(B) 2
(C) 3
(D) 4
हल:
यहाँ, A = {1, 2, 3}
तुल्यता सम्बन्ध जिसमें (1, 2) सम्मिलित हो ऐसे 2 सम्बन्ध हो सकते हैं।
अतः विकल्प (B) सही है।
प्रश्न 18.
मान लीजिए कि f :R → R है तब निम्नलिखित प्रकार से परिभाषित चिह्न फलन (signum Function) है।

तथा g : R → R, g(x) = [x] द्वारा प्रदत्त महत्तम पूर्णांक फलन है, जहाँ [x], x से कम या x के बराबर पूर्णांक है तो क्या fog तथा gof, अन्तराल [0, 1] में सम्पाती (coincide) हैं?
हल:
यहाँ f: R → R, जो
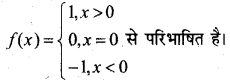
तथा g: R → R जो g(x) = [x] से परिभाषित है।
∴ x ϵ [0, 0, f(x) = 1, g(x) = 0.
gof (x) = g [f(x)] = g(1) = 1
तथा fog(x) = f(0)= 0
इस प्रकार fog ≠ gof
अतः अन्तराल (0, 1) में fog तथा gof सम्पाती नहीं हैं।
प्रश्न 19.
समुच्चय {a, b} में द्विआधारी संक्रियाओं की संख्या है
(A) 10
(B) 16
(C) 20
(D) 8
हल:
यहाँ समुच्चय {a, b}
समुच्चय A में 2 अवयव हैं।
द्विआधारी संक्रियाओं की संख्या = 24 = 16
अतः विकल्प (B) सही है।