MP Board Class 12th Maths Important Questions Chapter 3 आव्यूह

MP Board Class 12th Maths Important Questions Chapter 3 आव्यूह

आव्यूह Important Questions

आव्यूह वस्तुनिष्ठ प्रश्न

प्रश्न 1.
सही विकल्प चुनकर लिखिए –

प्रश्न 1.
यदि A = \(\begin{bmatrix} cos\alpha & -sin\alpha \\ sin\alpha & cos\alpha \end{bmatrix}\) तथा A + A’ = I, तो α का मान है –
(a) \(\frac { \pi }{ 6 } \)
(b) \(\frac { \pi }{ 3 } \)
(c) π
(d) \(\frac { 3\pi }{ 2 } \)
उत्तर:
(b) \(\frac { \pi }{ 3 } \)

प्रश्न 2.
यदि A = \(\left[\begin{array}{lll}
{2} & {0} & {0} \\
{0} & {2} & {0} \\
{0} & {0} & {2}
\end{array}\right]\) हो, तो A⁵ बराबर होगा –
(a) 5 A
(b) 10 A
(c) 16 A
(d) 32 A
उत्तर:
(c) 16 A

प्रश्न 3.
यदि एक आव्यूह सममित तथा विषम सममित दोनों ही है, तो –
(a) A एक विकर्ण आव्यूह है
(b) A एक शून्य आव्यूह है
(c) A एक वर्ग आव्यूह है
(d) A इनमें से कोई नहीं।
उत्तर:
(b) A एक शून्य आव्यूह है

प्रश्न 4.
यदि A = \(\begin{bmatrix} \alpha & \beta \\ \gamma & -\alpha \end{bmatrix}\) इस प्रकार है, कि A² = I तो –
(a) 1 + α² + βγ = 0
(b) 1 – α² + βγ = 0
(c) 1 – α² – βγ = 0
(d) 1 + α² – βγ = 0
उत्तर:
(c) 1 – α² – βγ = 0

प्रश्न 5.
यदि A = \(\begin{bmatrix} 2 & -1 \\ 3 & -2 \end{bmatrix}\) हो तो Aⁿ = ……………………………
(a) A = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\), यदि n सम प्राकृत संख्या
(b) A = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\), यदि n विषम प्राकृत संख्या
(c) A = \(\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\), यदि n ∈ N
(d) इनमें से कोई नहीं।
उत्तर:
(a) A = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\), यदि n सम प्राकृत संख्या

प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिए –

1. यदि A = \(\begin{bmatrix} 2 & 4 \\ 3 & 2 \end{bmatrix}\) तथा B = \(\begin{bmatrix} 1 & 3 \\ 2 & 5 \end{bmatrix}\) हो, तो AB का मान.
   …………………………………. होगा।
2. यदि A = diag [1, – 1, 2] तथा B = diag [2, 3, – 1] हो, तो 3A + 4B का मान ……………………………. होगा।
3. एक वर्ग आव्यूह A समशम आव्यूह कहलाता है, यदि ……………………………….
4. एक वर्ग आव्यूह A लाम्बिक आव्यूह कहलाता है, यदि …………………………..
5. यदि [x, 1] \(\begin{bmatrix} 1 & 0 \\ -2 & 0 \end{bmatrix}\) = 0, तो x का मान…………. होगा।

उत्तर:

1. \(\begin{bmatrix} 10 & 26 \\ 7 & 19 \end{bmatrix}\)
2. diag [11, 9, 2]
3. A² = A
4. AA’ = A’A = I
5. x = 2

प्रश्न 3.
निम्न कथनों में सत्य/असत्य बताइए –

1. गुणन संक्रिया क्रम-विनिमेय नियम का सदैव पालन करती है।
2. दो आव्यूह तुलनीय कहलाते हैं यदि उनमें पंक्तियों और स्तम्भों की संख्या समान हो।
3. यदि A एक वर्ग आव्यूह हो, तो A.adj A = |A|I होता है।
4. वर्ग आव्यूह A सममित आव्यूह कहलाती है, यदि A = -A^T।
5. आव्यूह A तथा B एक-दूसरे के व्युत्क्रम होंगे यदि AB = BA

उत्तर:

1. असत्य
2. सत्य
3. सत्य
4. असत्य
5. असत्य।

प्रश्न 4.
सही जोड़ी बनाइये –

उत्तर:

1. (d)
2. (e)
3. (a)
4. (b)
5. (c).

प्रश्न 5.
एक शब्द/वाक्य में उत्तर दीजिए –

1. यदि A और B एक ही क्रम के वर्ग आव्यूह हों तो Adj (AB) का मान क्या होगा?
2. एक वर्ग आव्यूह A प्रतिकेन्द्रज कहलाता है, यदि –
3. यदि A = \(\begin{bmatrix} 0 & i \\ i & 0 \end{bmatrix}\) हो, तो A² का मान होगा।
4. यदि A = [1, 2, 3], तो AA^T का मान ज्ञात कीजिए।
5. यदि x + Y = \(\begin{bmatrix} 1 & -2 \\ 3 & 4 \end{bmatrix}\) तथा X – Y = \(\begin{bmatrix} 3 & 2 \\ -1 & 0 \end{bmatrix}\) तो X का मान ज्ञात कीजिए।

उत्तर:

1. Adj.(AB) = (Adj B).(Adj A)
2. A² = I
3. – 1
4. [14]
5. \(\begin{bmatrix} 2 & 0 \\ 1 & 2 \end{bmatrix}\)

आव्यूह लघु उत्तरीय प्रश्न

प्रश्न 1.
यदि A = \(\begin{bmatrix} a^{ 2 }+b^{ 2 } & b^{ 2 }+c^{ 2 } \\ a^{ 2 }+c^{ 2 } & a^{ 2 }+b^{ 2 } \end{bmatrix}\) हो, तो A + B ज्ञात कीजिए।
हल:
A+ B = \(\begin{bmatrix} a^{ 2 }+b^{ 2 } & b^{ 2 }+c^{ 2 } \\ a^{ 2 }+c^{ 2 } & a^{ 2 }+b^{ 2 } \end{bmatrix}\) + \(\begin{bmatrix} 2ab & 2bc \\ -2ac & -2ab \end{bmatrix}\)

प्रश्न 2.
यदि A = \(\begin{bmatrix} cos^{ 2 }x & sin^{ 2 }x \\ sin^{ 2 }x & cos^{ 2 }x \end{bmatrix}\) तथा B = \(\begin{bmatrix} sin^{ 2 }x & cos^{ 2 }x \\ cos^{ 2 }x & sin^{ 2 }x \end{bmatrix}\) हो, तो A + B ज्ञात कीजिए। (NCERT)
हल:
A + B = \(\begin{bmatrix} cos^{ 2 }x & sin^{ 2 }x \\ sin^{ 2 }x & cos^{ 2 }x \end{bmatrix}\) + \(\begin{bmatrix} sin^{ 2 }x & cos^{ 2 }x \\ cos^{ 2 }x & sin^{ 2 }x \end{bmatrix}\)

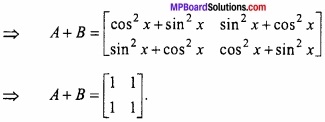
प्रश्न 3.
यदि A = \(\left[\begin{array}{lll}
{\frac{2}{3}} & {1} & {\frac{5}{3}} \\
{\frac{1}{3}} & {\frac{2}{3}} & {\frac{4}{3}} \\
{\frac{7}{3}} & {2} & {\frac{2}{3}}
\end{array}\right]\) तथा B = \(\left[\begin{array}{ccc}
{\frac{2}{5}} & {\frac{3}{5}} & {1} \\
{\frac{1}{5}} & {\frac{2}{5}} & {\frac{4}{5}} \\
{\frac{7}{5}} & {\frac{6}{5}} & {\frac{2}{5}}
\end{array}\right]\) हो, तो 3A – 5B परिकलित कीजिए।
हल:

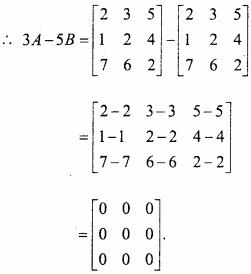
प्रश्न 4.
सरल कीजिए –
cos θ \(\begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix}\) + sin θ \(\begin{bmatrix} sin\theta & -cos\theta \\ cos\theta & sin\theta \end{bmatrix}\)
हल:

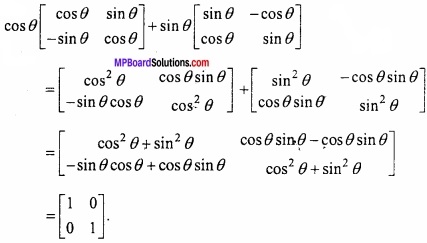
प्रश्न 5.
निम्नलिखित समीकरण से x तथा y के मानों को ज्ञात कीजिए – (NCERT)
2 \(\begin{bmatrix} x & 5 \\ 7 & y-3 \end{bmatrix}\) + \(\begin{bmatrix} 3 & -4 \\ 1 & 2 \end{bmatrix}\) = \(\begin{bmatrix} 7 & 6 \\ 15 & 14 \end{bmatrix}\)?
हल:
दिया है –

समान आव्यूह की परिभाषा से,
2x + 3 = 7
⇒ 2x = 4 ⇒ x = 2
⇒ 2y – 4 = 14
⇒ 2y = 18 ⇒ y = 9
∴ x = 2, y = 9

प्रश्न 6.
X तथा Y ज्ञात कीजिए यदि X + Y = \(\begin{bmatrix} 5 & 2 \\ 0 & 9 \end{bmatrix}\) तथा X – Y = \(\begin{bmatrix} 3 & 6 \\ 0 & -1 \end{bmatrix}\) है। (NCERT)
हल:
दिया है:
X + Y = \(\begin{bmatrix} 5 & 2 \\ 0 & 9 \end{bmatrix}\) ……………………………. (1)
तथा
X – Y = \(\begin{bmatrix} 3 & 6 \\ 0 & -1 \end{bmatrix}\) ……………………………….. (2)
समी. (1) और (2) को जोड़ने पर,
2X = \(\begin{bmatrix} 5 & 2 \\ 0 & 9 \end{bmatrix}\) + \(\begin{bmatrix} 3 & 6 \\ 0 & -1 \end{bmatrix}\)

समी. (1) में (2) को घटाने पर,

प्रश्न 7.
x तथा y ज्ञात कीजिए यदि
2 \(\begin{bmatrix} 1 & 3 \\ 0 & x \end{bmatrix}\) + \(\begin{bmatrix} y & 0 \\ 1 & 2 \end{bmatrix}\) = \(\begin{bmatrix} 5 & 6 \\ 1 & 8 \end{bmatrix}\)? (NCERT)
हल:
दिया है:
2 \(\begin{bmatrix} 1 & 3 \\ 0 & x \end{bmatrix}\) + \(\begin{bmatrix} y & 0 \\ 1 & 2 \end{bmatrix}\) = \(\begin{bmatrix} 5 & 6 \\ 1 & 8 \end{bmatrix}\)

समान आव्यूह की परिभाषा से,
2 + y = 5 ⇒ y = 3
2x + 2 = 8
⇒ x + 1 = 4
⇒ x = 3
∴ x = 3, y = 3.

प्रश्न 8.
यदि \(\left[\begin{array}{c}
{x+y+z} \\
{x+z} \\
{y+z}
\end{array}\right]\) = [ \(\begin{matrix} 9 \\ 5 \\ 7 \end{matrix}\) ] हो तो x, yतथा z के मान कीजिये
हल:
दिया है:
\(\left[\begin{array}{c}
{x+y+z} \\
{x+z} \\
{y+z}
\end{array}\right]\) = [ \(\begin{matrix} 9 \\ 5 \\ 7 \end{matrix}\) ]
सामान आतुयह की परोबाशा से
x + y + 2 = 9
x+ z = 5
y + z = 7
समी. (1) और (2) से,
x + z + y = 9
⇒ 5 + y = 9
⇒ y = 4
समी. (1) और (3) से,
x + (y + z) = 9
⇒ x + 7 = 9
⇒ x = 2
x का मान समी. (2) में रखने पर,
2 + z = 5
⇒ z = 3
∴ x = 2, y = 4, z = 3.

प्रश्न 9.
यदि
\(\begin{bmatrix} x+y & 2 \\ 5+z & xy \end{bmatrix}\) = \(\begin{bmatrix} 6 & 2 \\ 5 & 8 \end{bmatrix}\)
हो, तो x, y तथा z के मान ज्ञात कीजिए। (NCERT)
हल:
दिया है:
\(\begin{bmatrix} x+y & 2 \\ 5+z & xy \end{bmatrix}\) = \(\begin{bmatrix} 6 & 2 \\ 5 & 8 \end{bmatrix}\)
समान आव्यूह की परिभाषा से,
x + y = 6 …………………………. (1)
xy = 8 ………………………… (2)
5 + z = 5
⇒ z = 0
समी. (1) से,
y = 6 – x
xy = 8
⇒ x (6 – x) = 8
⇒ 6x – x² = 8
⇒ x² – 6x + 8 = 0
⇒ x² – 4x – 2x + 8 = 0
⇒ x(x – 4) – 2(x – 4) = 0
⇒ (x – 2) (x – 4) = 0
⇒ x = 2, 4
जब x = 2 तब y = 6 – 2 = 4
जब x = 4 तब y = 6 – 4 = 2
अतः
x = 2, y = 4, z = 0
x = 4, y = 2, z = 0.

प्रश्न 10.
यदि A = \(\begin{bmatrix} 1 & -1 \\ 2 & 3 \end{bmatrix}\) हो, तो सिद्ध कीजिए A² – 4A + 5I = 0?
हल:
दिया है
A = \(\begin{bmatrix} 1 & -1 \\ 2 & 3 \end{bmatrix}\)
A² = A. A = \(\begin{bmatrix} 1 & -1 \\ 2 & 3 \end{bmatrix}\) \(\begin{bmatrix} 1 & -1 \\ 2 & 3 \end{bmatrix}\)

प्रश्न 11.
यदि A = \(\begin{bmatrix} 2 & -3 \\ 3 & 4 \end{bmatrix}\) हो, तो सिद्ध कीजिए A² – 6A + 17I = 0?
हल:
A = \(\begin{bmatrix} 2 & -3 \\ 3 & 4 \end{bmatrix}\)
A² = A.A = \(\begin{bmatrix} 2 & -3 \\ 3 & 4 \end{bmatrix}\) \(\begin{bmatrix} 2 & -3 \\ 3 & 4 \end{bmatrix}\)

प्रश्न 12.
यदि A = \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}\) हो, तो सिद्ध कीजिए कि A² – 5A + 7I = 0? (NCERT)
हल:
A² = A.A = \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}\) × \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}\)

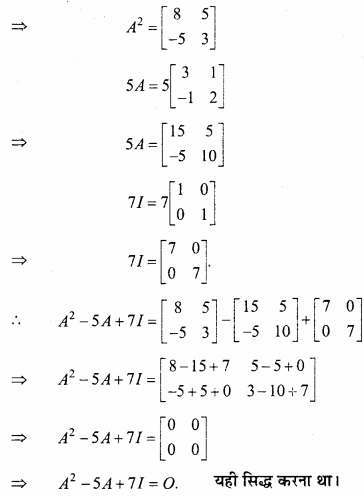
प्रश्न 13.
यदि A = \(\begin{bmatrix} 3 & -2 \\ 4 & -2 \end{bmatrix}\) और I = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\) हो, तो k का मान ज्ञात कीजिए यदि A² = KA – 2I? (NCERT)
हल:
माना A² = kA – 2I
⇒ kA = A² + 2I

प्रश्न 14.
यदि f (x) = x² – 2x – 3, तो f (A) ज्ञात कीजिए जब A = \(\begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix}\)?
हल:
f (x) = x² – 2x – 3
∴ f (A) = A² – 24A – 3I

प्रश्न 15.
यदि आव्यूह A = \(\left[\begin{array}{ccc}
{0} & {a} & {-3} \\
{2} & {0} & {-1} \\
{b} & {1} & {0}
\end{array}\right]\) विषम सममित है तो ‘a’ तथा ‘b’ के मान ज्ञात कीजिये। (CBSE 2018)
हल:
यदि A आव्यूह विषम सममित है तो A’ = – A

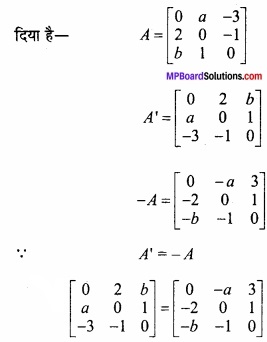
2 = – a या a = – 2
– 3 = – b या b = 3.

प्रश्न 16.
यदि A = \(\begin{bmatrix} cos\alpha & -sin\alpha \\ sin\alpha & cos\alpha \end{bmatrix}\) है तो सिद्ध कीजिए –
AA^-1 = I?
हल:
दिया है:
A = \(\begin{bmatrix} cos\alpha & -sin\alpha \\ sin\alpha & cos\alpha \end{bmatrix}\)
A^-1 = \(\frac { adjA }{ |A| } \)
|A| = \(\begin{vmatrix} cos\alpha & -sin\alpha \\ sin\alpha & cos\alpha \end{vmatrix}\)
= cos² α – ( – sin² α)
= cos² α + sin² α = 1
∴ |A| = 1 …………………………….. (1)

प्रश्न 17.
यदि A = \(\begin{bmatrix} cos\alpha & -sin\alpha \\ sin\alpha & cos\alpha \end{bmatrix}\) है तो सिद्ध कीजिए –
A. (Adj A) = |A|I?
हल:

प्रश्न 18.
सिद्ध कीजिए कि वर्ग आव्यूह A = \(\begin{vmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{vmatrix}\) लाम्बिक आव्यूह है। [
हल:

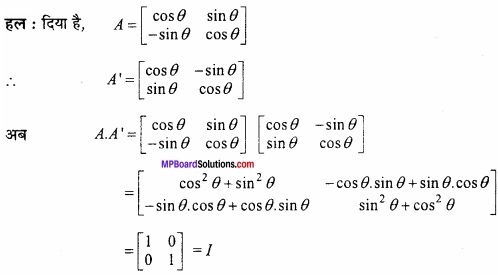
इसी प्रकार A’. A = I
तब A. A’ = A’. A = I
अतः A लाम्बिक आव्यूह है। यही सिद्ध करना था।

प्रश्न 19.
यदि A = \(\begin{bmatrix} 3 & 2 \\ 7 & 5 \end{bmatrix}\) तथा B = \(\begin{bmatrix} 6 & 7 \\ 8 & 9 \end{bmatrix}\) हो, तो (AB)^-1 का मान ज्ञात कीजिए।
हल:
दिया है,
A = \(\begin{bmatrix} 3 & 2 \\ 7 & 5 \end{bmatrix}\), B = \(\begin{bmatrix} 6 & 7 \\ 8 & 9 \end{bmatrix}\)
A. B = \(\begin{bmatrix} 3 & 2 \\ 7 & 5 \end{bmatrix}\) \(\begin{bmatrix} 6 & 7 \\ 8 & 9 \end{bmatrix}\)

प्रश्न 20.
यदि A = \(\begin{bmatrix} 2 & -3 \\ -4 & 7 \end{bmatrix}\) हो, तो सिद्ध कीजिए कि
2A^-1 = 9I – A? (CBSE 2018)
हल:
दिया है,
A = \(\begin{bmatrix} 2 & -3 \\ -4 & 7 \end{bmatrix}\)

अतः समी (1) और (2) से,
2A^-1 = 9I – A

प्रश्न 21.
A तथा B आव्यूहों के लिए सत्यापित कीजिए कि (AB)’ = B’A’ जहाँ A = [ \(\begin{matrix} 1 \\ -4 \\ 3 \end{matrix}\) ] B = [-1 2 1]? (NCERT)
हल:
AB = [ \(\begin{matrix} 1 \\ -4 \\ 3 \end{matrix}\) ] _3×1 [ \(\begin{matrix} -1 & 2 & 3 \end{matrix}\) ] _1×3



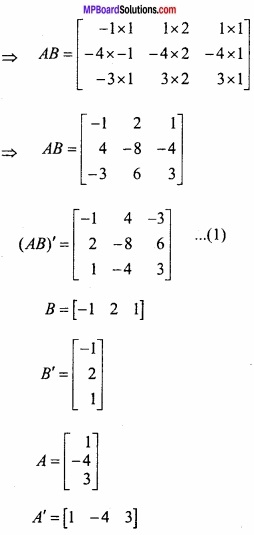
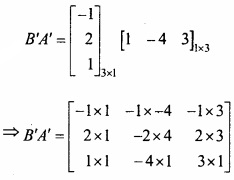
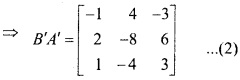
अतः समी (1) और (2) से,
(AB)’ = B’A’

आव्यूह दीर्घ उत्तरीय प्रश्न – II

प्रश्न 1.
यदि A = \(\begin{bmatrix} 1 & 4 \\ 3 & 5 \end{bmatrix}\) हो, तो सिद्ध कीजिए कि –
A. adj A = (adjA). A = (adj A). A = |A| I?
हल:
दिया है,
A = \(\begin{bmatrix} 1 & 4 \\ 3 & 5 \end{bmatrix}\)
तब
|A| = \(\begin{bmatrix} 1 & 4 \\ 3 & 5 \end{bmatrix}\) = 5 – 12 = -7
A₁₁, A₁₂ = – 3, A₂₁ = – 4, A₂₂ = 1

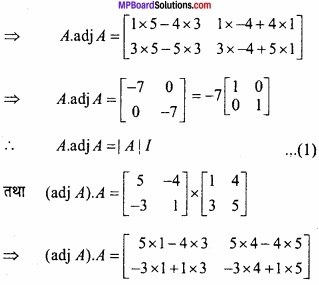
⇒ (adj A). A = \(\begin{bmatrix} -7 & 0 \\ 0 & -7 \end{bmatrix}\)
⇒ (adj A). A = – 7 \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\)
⇒ (adj A).A = |A| I ………………………….. (2)
अतः समी (1) और (2) से,
A.adj A = (adjA). A = |A| I. यही सिद्ध करना था।

प्रश्न 2.
यदि A = \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\) हो, तो सिद्ध कीजिए कि A^-1 = A?
हल:
प्रश्न क्र. 1 की भाँति हल करें।

प्रश्न 3.
यदि आव्यूह A = \(\left[\begin{array}{lll}
{0} & {0} & {1} \\
{0} & {1} & {0} \\
{1} & {0} & {0}
\end{array}\right]\) हो, तो सिद्ध कीजिए कि A^-1 = A?
हल:
दिया है:
A = \(\left[\begin{array}{lll}
{0} & {0} & {1} \\
{0} & {1} & {0} \\
{1} & {0} & {0}
\end{array}\right]\)

प्रश्न 4.
आव्यूह A = \(\left[\begin{array}{lll}
{2} & {3} & {1} \\
{3} & {4} & {1} \\
{3} & {7} & {2}
\end{array}\right]\) का प्रतिलोम ज्ञात कीजिए।
हल:
दिया है,
A = \(\left[\begin{array}{lll}
{2} & {3} & {1} \\
{3} & {4} & {1} \\
{3} & {7} & {2}
\end{array}\right]\)
∴ |A| = 2(4 × 2 – 7 × 1) – 3(3 × 2 – 3 × 1) + 1(3 × 7 – 3 × 4)
= 2(8 – 7) – 3(6 – 3) + 1(21 – 12)
= 2(1) – 3(3) + 1(9)
= 2 – 9 + 9 = 2
स्पष्ट है कि |A| ≠ 0
अतः A^-1 का अस्तित्व है।
अब |A| के अवयवों का सहखण्ड है –
A₁₁ = +(8 – 7) = 1, A₁₂ = -(6 – 3) = -3
A₁₃ = +(21 – 12) = 9, A₂₁ = -(6 – 7) = 1
A₂₂ = +(4 – 3) = 1, A₂₃ = -(14 – 9) = -5
A₃₁ = +(3 – 4) = -1, A₃₂ = -(2 – 3) = 1
A₃₃ = +(8 – 9) = -1

प्रश्न 5.
यदि A = \(\left[\begin{array}{lll}
{1} & {2} & {3} \\
{2} & {4} & {5} \\
{3} & {5} & {6}
\end{array}\right]\) हो, तो A^-1 का मान ज्ञात कीजिए।
हल: प्रश्न क्र. 4 की भाँति हल कीजिए।
उत्तर:
\(\left[\begin{array}{lll}
{1} & {2} & {3} \\
{2} & {4} & {5} \\
{3} & {5} & {6}
\end{array}\right]\)

प्रश्न 6.
यदि A = \(\left[\begin{array}{lll}
{1} & {2} & {2} \\
{2} & {1} & {2} \\
{2} & {2} & {1}
\end{array}\right]\) हो, तो A^-1 का मान ज्ञात कीजिए।
हल:
दिया है, A = \(\left[\begin{array}{lll}
{1} & {2} & {2} \\
{2} & {1} & {2} \\
{2} & {2} & {1}
\end{array}\right]\)
|A| = \(\left[\begin{array}{lll}
{1} & {2} & {2} \\
{2} & {1} & {2} \\
{2} & {2} & {1}
\end{array}\right]\)
⇒ |A| = 1(1 – 4) + 2(4 – 2) + 2 (4 – 2)
= – 3 + 4 + 4 = 5
|A| ≠ 0, इसलिए A^-1 का अस्तित्व है।

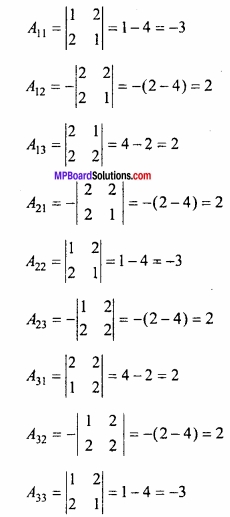
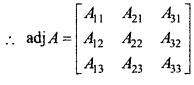
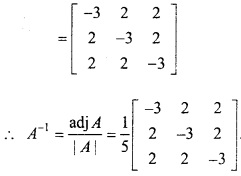
प्रश्न 7.
यदि A = \(\begin{bmatrix} 2 & 3 \\ -1 & 0 \end{bmatrix}\) हो, तो सिद्ध कीजिए कि –
A² – 2A + 3I = 0?17
हल:
दिया है,
A = \(\begin{bmatrix} 2 & 3 \\ -1 & 0 \end{bmatrix}\)

प्रश्न 8.
यदि A = \(\begin{bmatrix} 2 & -3 \\ 3 & 4 \end{bmatrix}\) हो, तो दर्शािइये कि A² – 6A + 17I = 0 तथा A^-1 का मान ज्ञात कीजिए।
हल:
दिया है:
A = \(\begin{bmatrix} 2 & -3 \\ 3 & 4 \end{bmatrix}\)

प्रश्न 9.
यदि A = \(\begin{bmatrix} -8 & 5 \\ 2 & 4 \end{bmatrix}\) हो, तो दर्शाइये A² + 4A – 42I = 0 तथा A^-1 का मान ज्ञात कीजिए।
हल:
प्रश्न क्र. 8 की भाँति हल कीजिए।
उत्तर:
A^-1 = \(\frac{1}{42}\) \(\begin{bmatrix} -4 & 5 \\ 2 & 0 \end{bmatrix}\)

प्रश्न 10.
आव्यूह विधि से निम्न समीकरणों को हल कीजिए –
x + y + 2 = 3
2x – y + z = 2
x – 2y + 3z = 2
हल:
यहाँ A = \(\left[\begin{array}{lll}
{1} & {1} & {1} \\
{2} & {-1} & {1} \\
{1} & {-2} & {3}
\end{array}\right]\), X = [ \(\begin{matrix} x \\ y \\ z \end{matrix}\) ] तथा B = [ \(\begin{matrix} 3 \\ 2 \\ 2 \end{matrix}\) ]

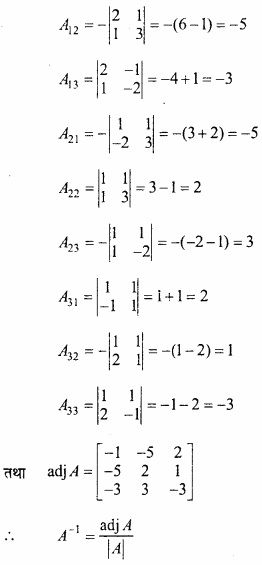
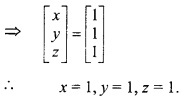
प्रश्न 11.
आव्यूह विधि से निम्न समीकरण हल कीजिये।
x + y + z = 6
x + 2y + 3z = 14
x + 4y + 9z = 36?
हल:
दिया गया समीकरण निकाय है –
x + y + z = 6
x + 2y + 3z = 14
x + 4y + 9z = 36.
उपरोक्त समीकरण निकाय का आव्यूह रूप है –
AX = B

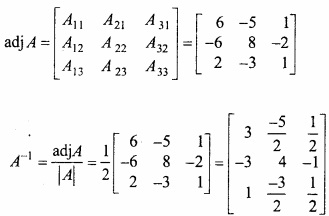
प्रश्न 12.
यदि A’ = \(\left[\begin{array}{rr}
{3} & {4} \\
{-1} & {2} \\
{0} & {1}
\end{array}\right]\) तथा B = \(\left[\begin{array}{rrr}
{-1} & {2} & {1} \\
{1} & {2} & {3}
\end{array}\right]\) है तो सत्यापित कीजिये की

(i) (A + B)’ = A’ + B’
(ii) (A – B)’ = A’ – B’ (NCERT)

हल:




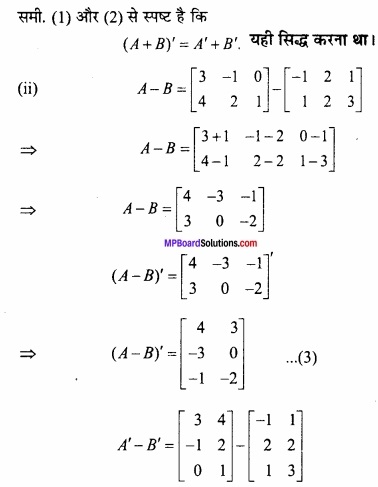
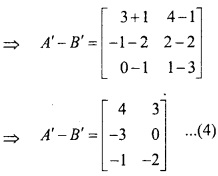
अतः समी (1) और (4) से,
(A – B)’ = A’ – B’ यही सिद्ध करना था।

प्रश्न 13.
यदि A = \(\left[\begin{array}{rrr}
{-1} & {2} & {3} \\
{5} & {7} & {9} \\
{-2} & {1} & {1}
\end{array}\right]\) तथा B = \(\left[\begin{array}{rrr}
{-4} & {1} & {-5} \\
{1} & {2} & {0} \\
{1} & {3} & {1}
\end{array}\right]\) हो, तो सत्यापित कीजिए कि
(i) (A + B)’ = A’ + B’
(ii) (A – B)’ = A’ – B’
हल:
प्रश्न क्र. 12 की भाँति हल करें। (NCERT)

प्रश्न 14.
आव्यूह A = \(\begin{bmatrix} 3 & 5 \\ 1 & -1 \end{bmatrix}\) को सममित और विषम सममित आव्यूह के योग के रूप में प्रदर्शित कीजिए? (NCERT)
हल:

प्रश्न 15.
(A) प्रारंभिक संक्रियाओं का प्रयोग करते हुए आव्यूह A = \(\begin{bmatrix} 2 & 3 \\ 5 & 7 \end{bmatrix}\) का व्युत्क्रम ज्ञात कीजिए? (NCERT)
हल:
A = AI के प्रयोग से,

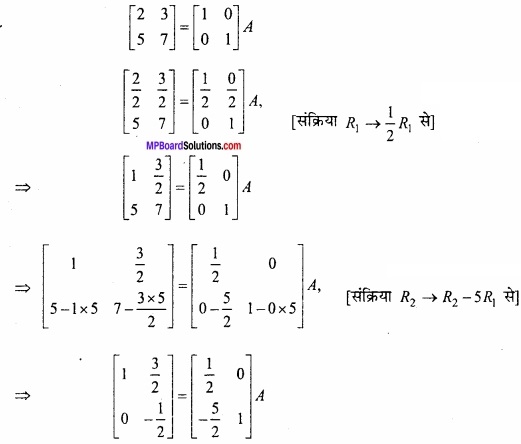
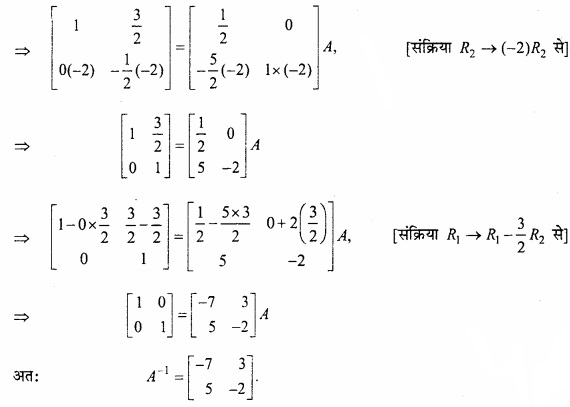
(B)
प्रारंभिक संक्रियाओं का प्रयोग करते हुए आव्यूह A = \(\begin{bmatrix} 3 & 10 \\ 2 & 7 \end{bmatrix}\) का व्युत्क्रम ज्ञात कीजिए। (NCERT)
हल: प्रश्न क्र. 15 (A) की भाँति हल करें।
उत्तर- \(\begin{bmatrix} 7 & -10 \\ -2 & 3 \end{bmatrix}\)

प्रश्न 16.
आव्यूह विधि के प्रयोग से निम्नलिखित समीकरण निकाय को हल कीजिए – (NCERT)
\(\frac{2}{x}\) + \(\frac{3}{y}\) + \(\frac{10}{z}\) = 4 (CBSE 2011)
\(\frac{4}{x}\) – \(\frac{6}{y}\) + \(\frac{5}{z}\) = 1
\(\frac{6}{x}\) + \(\frac{9}{y}\) – \(\frac{20}{z}\) = 2, x, y, z, ≠ 0
हल:
माना
\(\frac{1}{x}\) = u, \(\frac{1}{y}\) = v, \(\frac{1}{z}\) = w, तब
2u+ 3v+ 10w = 4
4u – 6v + 5w = 1
6u + 9v – 20w = 2
उपरोक्त समीकरण निकाय का आव्यूह रूप है –
AX = B

⇒ |A| = 2 × (120 – 45) – 3(-80 – 30) + 10(36 + 36)
⇒ |A| = 150 + 330 + 720 = 1200
⇒ |A| ≠ 0 अर्थात् A व्युत्क्रमणीय है।
अतः समीकरण निकाय संगत है और अद्वितीय हल निम्न है –
X = A^-1 B
माना A में अवयव a_ij का सहखण्ड A_ij है, तब

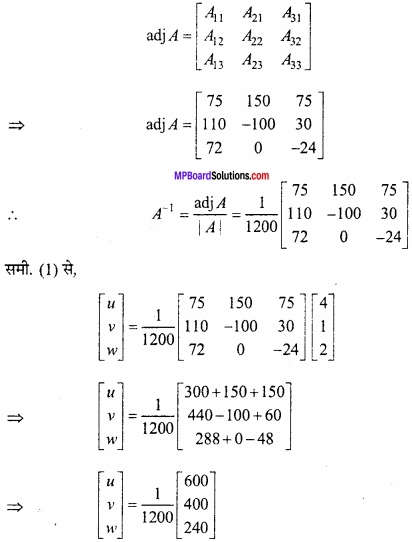
प्रश्न 17.
A^-1 ज्ञात कीजिये जहाँ इसकी सहायता से निम्न निम्न समीकरण निकाय को हल कीजिये –
x + 2y – 3z = -4
2x + 3y + 2z = 2
3x – 3y – 4z = 11 (CBSE 2008, 10, 12)
हल:

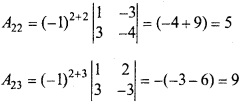
प्रश्न 18.
\(\left[\begin{array}{ccc}
{-4} & {4} & {4} \\
{-7} & {1} & {3} \\
{5} & {-3} & {-1}
\end{array}\right]\) \(\left[\begin{array}{ccc}
{1} & {-1} & {1} \\
{1} & {-2} & {-2} \\
{2} & {1} & {3}
\end{array}\right]\) का गुणनफल ज्ञात कीजिए तथा इसकी सहायता से समीकरण निकाय को हल कीजिए – (CBSE 2012)
x – y + z = 4
x – 2y – 2x = 9
2x + y + 3z = 1.
हल:
माना B = \(\left[\begin{array}{ccc}
{-4} & {4} & {4} \\
{-7} & {1} & {3} \\
{5} & {-3} & {-1}
\end{array}\right]\) और A = \(\left[\begin{array}{ccc}
{1} & {-1} & {1} \\
{1} & {-2} & {-2} \\
{2} & {1} & {3}
\end{array}\right]\)

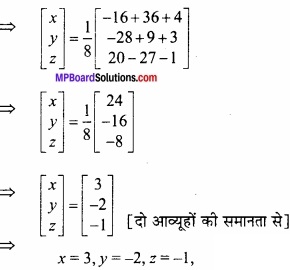
प्रश्न 19.
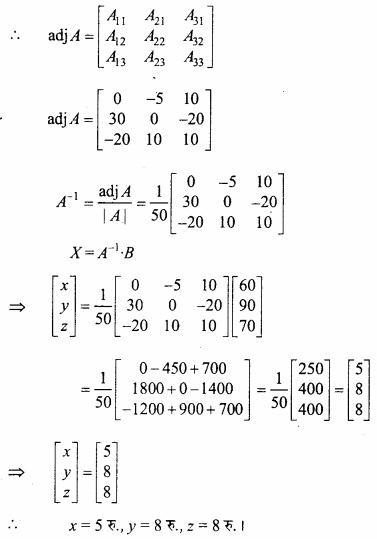
4kg प्याज, 3kg गेहूँ और 2kg चावल का मूल्य 60 रु. है। 2kg प्याज, 4kg गेहूँ और 6kg चावल का मूल्य 90 रु. है। 6kg प्याज, 2kg गेहूँ और 3kg चावल का मूल्य 70 रु. है। आव्यूह विधि द्वारा प्रत्येक का मूल्य प्रति kg ज्ञात कीजिए।
हल:
माना 1 kg प्याज का मूल्य = x रु.
1 kg गेहूँ का मूल्य = y रु.
1 kg चावल का मूल्य = zरु.
प्रश्नानुसार,
4x + 3y + 2z = 60
2x + 4y + 6z = 90
6x + 2y + 3z = 70
आव्यूह रूप है –
AX = B

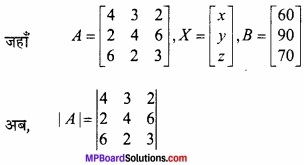
⇒ |A| = 4(12 – 12) – 3(6 – 36) + 2(4 – 24)
⇒ |A| = 0 + 90 – 40 = 50 ≠ 0
⇒ A^-1 का अस्तित्व है।
अतः समीकरण निकाय का अद्वितीय हल है –
X = A^-1 B
माना A में a_ij का सहखण्ड A_ij है, तब

MP Board Class 12 Maths Important Questions