ΨMP Board Class 12th Maths Important Questions Chapter 2 Inverse Trigonometric Functions
Inverse Trigonometric Functions Important Questions
Inverse Trigonometric Functions Objective Type Questions:
Question 1.
Choose the correct answer:
Question 1.
If sin-1x – cos -1 x = \(\frac { \pi }{ 6 } \), then the value of x is equal to:
(a) \(\frac{1}{2}\)
(b) \(\frac { \sqrt { 3 } }{ 2 } \)
(c) \(\frac{-1}{2}\)
(d) None of these
Answer:
(a) \(\frac{1}{2}\)
Question 2.
If tan-13 + tan-1 8, then the value of x is equal to:
(a) \(\frac { \pi }{ 2 } \)
(b) \(\frac { \pi }{ 3 } \)
(c) \(\frac { \pi }{ 4 } \)
(d) \(\frac { -3\pi }{ 4 } \)
Answer:
(b) \(\frac { \pi }{ 3 } \)
Question 3.
tan-1 \(\frac{x}{y}\) + tan-1 \(\frac{x-y}{x+y}\) is equal to:
(a) \(\frac { \pi }{ 2 } \)
(b) \(\frac { \pi }{ 3 } \)
(c) \(\frac { \pi }{ 4 } \)
(d) \(\frac { -3\pi }{ 4 } \)
Answer:
(c) \(\frac { \pi }{ 4 } \)
![]()
Question 4.
The value of 2 tan-1 {cosec (tan-1 x ) – tan (cot-1 x)} is equal to:
(a) cot-1x
(b) cot-1\(\frac{1}{x}\)
(c) tan-1x
(d) tan-1\(\frac{1}{x}\)
Answer:
(c) tan-1x
Question 5.
The value of tan{cos-1\(\frac { 1 }{ 5\sqrt { 2 } } \) – sin-1 \(\frac { 4 }{ \sqrt { 17 } } \)} is equal to:
(a) \(\frac { \sqrt { 29 } }{ 3 } \)
(b) \(\frac{29}{3}\)
(c) \(\frac { \sqrt { 3 } }{ 29 } \)
(d) \(\frac{3}{29}\)
Answer:
(d) \(\frac{3}{29}\)
Question 2.
Fill in the blanks:
- tan-1(1) + tan-1(2) + tan-1 (3) = …………………………..
- tan-1(2) – tan-1 (1) = …………………………..
- cot-1 3 + cosec-1 \(\sqrt { 5 } \) = ……………………………
- sin(sin-1 x + 2 cos-1 x) = ……………………………….
- If sin-1(\(\frac { 2a }{ 1+a^{ 2 } } \)) + sin-1 (\(\frac { 2b }{ 1+b^{ 2 } } \)) = 2 tan-1 x, then x = ……………………….
- If tan-1 \(\frac{1-x}{1+x}\) = \(\frac{1}{2}\) tan-1 x ( When x > 0), then x = ………………………..
- tan-1\(\frac{a-b}{1+ab}\) + tan-1\(\frac{b-c}{1+bc}\) + tan-1c = ………………………….
Answer:
- π
- tan-1\(\frac{1}{3}\)
- \(\frac{π}{4}\)
- x
- \(\frac{a+b}{1-ab}\)
- \(\frac { 1 }{ \sqrt { 3 } } \)
- tan-1 (a)
![]()
Question 3.
Write True/False:
- tan-1x + tan-1 y = tan-1\(\frac{x+y}{1-xy}\)
- cos-1(-x) = – cos-1 x
- sin-1(3x – 4x3) = sin-1 \(\frac{x}{3}\)
- cos-1 (\(\frac { 1-x^{ 2 } }{ 1+x^{ 2 } } \)) = 2 tan-1x
- sin-1x – sin-1[xy – \(\sqrt { 1-x^{ 2 } } \) \(\sqrt { 1-y^{ 2 } } \)]
Answer:
- True
- False
- False
- True
- False
Question 4.
Match the column:
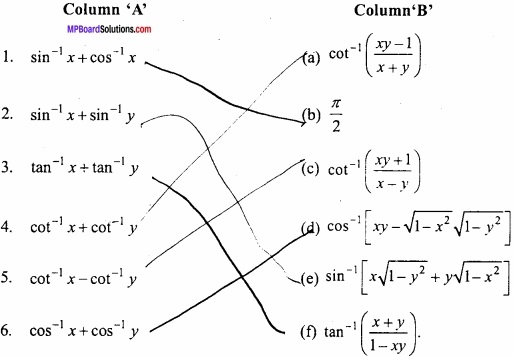
Answer:
- (b)
- (e)
- (f)
- (a)
- (c)
- (d)
![]()
Question 5.
Write the answer in one word/sentence:
- Find the value of tan-1\(\frac{1}{2}\) + tan-1\(\frac{3}{2}\)
- Find the value of tan-1\(\frac { x }{ \sqrt { 1-x^{ 2 } } } \)
- Find the value of sin ( 2 sin-1\(\frac{3}{5}\))
- Solve the equation: sin-1\(\frac{x}{5}\) + cosec -1\(\frac{5}{4}\) = \(\frac { \pi }{ 2 } \)
- Write the principal value of cos-1 (cos \(\frac { 7\pi }{ 6 } \))
- If cos-1 (\(\frac{1}{x}\)) = θ, then find the value of tan θ
Answer:
- tan-1 8
- sin-1x
- \(\frac{24}{25}\)
- x = 3
- \(\frac { 5\pi }{ 6 } \)
- \(\sqrt { x^{ 2 }-1 } \)
Inverse Trigonometric Functions Very Short Answer Type Questions
Question 1.
Find the principle value of the following?
- tan-1[sin(- \(\frac { \pi }{ 2 } \)) ] (CBSE 2014)
- cot [ \(\frac { \pi }{ 2 } \) – 2 cot-1 \(\sqrt{3}\) ] (CBSE 2014)
- tan-1(- \(\sqrt{3}\) )
- sec-1 ( \(\frac{-2}{3}\) \(\sqrt{3}\) ) (NCERT)
- cosec-1(2) (NCERT)
Solution:
1. Let, tan-1[ sin(- \(\frac { \pi }{ 2 } \) ) = θ
⇒ tan-1 [-sin \(\frac { \pi }{ 2 } \) ] = θ
⇒ tan-1 (-1) = θ
⇒ tan θ = 1
⇒ tan θ = – tan \(\frac { \pi }{ 4 } \)
⇒ tan θ = tan ( \(\frac { -\pi }{ 4 } \) )
θ = \(\frac { -\pi }{ 4 } \)
∴ The principle value is \(\frac { -\pi }{ 4 } \)
2. cot(\(\frac { -\pi }{ 2 } \) – cot-1 \(\sqrt{3}\))
Let cot-1 \(\sqrt{3}\) = θ
⇒ cot θ = \(\sqrt{3}\)
⇒ cot θ = cot \(\frac { \pi }{ 6 } \)
∴ θ = \(\frac { \pi }{ 6 } \)
∴ cot ( \(\frac { \pi }{ 2 } \) – cot-1\(\sqrt{3}\) ) = cot (\(\frac { \pi }{ 2 } \) – 2 × \(\frac { \pi }{ 6 } \))
= cot ( \(\frac { \pi }{ 2 } \) – \(\frac { \pi }{ 3 } \) )
= cot \(\frac { \pi }{ 6 } \)
= \(\sqrt{3}\)
∴ The principal value is \(\sqrt{3}\)
3. Let tan(- \(\sqrt{3}\)) = θ
⇒ tan θ = – \(\sqrt{3}\)
⇒ tan θ = – tan (\(\frac { \pi }{ 3 } \))
⇒ tan θ = tan (- \(\frac { \pi }{ 3 } \))
⇒ θ = – \(\frac { \pi }{ 3 } \)
Hence the principle value is – \(\frac { \pi }{ 3 } \)
4. Let sec-1( \(\frac{-2}{3}\) \(\sqrt{3}\) ) = θ
⇒ sec-1( \(\frac { -2 }{ \sqrt { 3 } } \) ) = θ
⇒ sec θ = \(\frac { -2 }{ \sqrt { 3 } } \)
⇒ sec θ = – sec ( \(\frac { \pi }{ 6 } \) )
⇒ sec θ = sec (π – \(\frac { \pi }{ 6 } \) )
⇒ sec θ = sec \(\frac { 5\pi }{ 6 } \)
∴θ = \(\frac { 5\pi }{ 6 } \)
The principle value is \(\frac { 5\pi }{ 6 } \)
5. Let cosec-1(2) = θ
⇒ cosec θ = 2
⇒ cosec θ = cosec \(\frac { \pi }{ 6 } \) θ ∈ [- \(\frac { \pi }{ 2 } \), \(\frac { \pi }{ 2 } \) ]
The principle value is \(\frac { \pi }{ 6 } \).
![]()
Question 2.
Prove the following:
- 2 cos-1(\(\frac{4}{5}\)) = cos-1( \(\frac{7}{25}\) )
- 2 sin-1( \(\frac{5}{13}\) ) = sin-1( \(\frac{120}{169}\) )
- 2 sin-1( \(\frac{3}{5}\) ) = sin-1( \(\frac{24}{25}\) )
Solution:
1. 2 cos-1( \(\frac{4}{5}\) ) = cos-1( \(\frac{7}{25}\) )
Formula 2 cos-1 x = cos-1(2x2 – 1)
∴ L.H.S = 2 cos-1( \(\frac{4}{5}\) )
= cos-1 (2 \(\frac{16}{25}\) – 1)
= cos-1 ( \(\frac{32}{25}\) – 1)
= cos-1( \(\frac{32-25}{25}\) )
= cos-1\(\frac{7}{25}\)
= R.H.S.
2. 2 sin-1\(\frac{3}{5}\) = sin-1\(\frac{24}{25}\)
Formula 2 sin-1(x) = sin-1(2x\(\sqrt { 1-x^{ 2 } } \))
∴ 2 sin-1 \(\frac{3}{5}\) = sin-1[2. \(\frac{3}{5}\) \(\sqrt { 1-\frac { 9 }{ 25 } } \)]
= sin-1[ \(\frac{6}{5}\) \(\sqrt { \frac { 16 }{ 25 } } \) ]
= sin-1[ \(\frac{6}{5}\) . \(\frac{4}{5}\) ]
= sin-1[ \(\frac{24}{25}\) ]
= R.H.S. Proved.
3. 2 sin-1(\(\frac{5}{13}\)) = sin-1\(\frac{120}{169}\)
Solve like Q.2(b)
![]()
Question 3.
Find the value of tan-1{2 cos(2 sin-1\(\frac{1}{2}\)} (CBSE 2013, NCERT)
Solution:
tan-1[2 cos(2 sin-1\(\frac{1}{2}\)) ]
= tan-1[ 2 cos (2 sin-1 sin \(\frac { \pi }{ 6 } \)) ]
= tan-1[ 2 cos (2. \(\frac { \pi }{ 6 } \)) ]
= tan-1[ 2 cos \(\frac { \pi }{ 3 } \) ]
= tan-1 [ 2. \(\frac{1}{2}\) ]
= tan-1 1
= \(\frac { \pi }{ 4 } \).
Question 4.
Find the value of sin [ \(\frac { \pi }{ 3 } \) – sin-1( \(\frac{-1}{2}\) ) ]? [CBSE 2008, 2013]
Solution:
sin[ \(\frac { \pi }{ 3 } \) – sin-1(\(\frac{-1}{2}\) ) ] = sin-1 [ \(\frac { \pi }{ 3 } \) – ( – sin-1\(\frac{1}{2}\) ) ]
= sin-1 [ \(\frac { \pi }{ 3 } \) + sin-1 sin\(\frac { \pi }{ 6 } \) ]
= sin-1 [ \(\frac { \pi }{ 3 } \) + \(\frac { \pi }{ 6 } \) ]
= sin-1 ( \(\frac { \pi }{ 2 } \) )
= 1.
Question 5.
Prove that:
2 tan-1\(\frac{1}{5}\) = tan-1 ( \(\frac{5}{12}\) )
Solution:
2 tan-1( \(\frac{1}{5}\) ) = tan-1 ( \(\frac{5}{12}\) )
L.H.S. = 2 tan-1 ( \(\frac{1}{5}\) )

= tan-1 [ \(\frac{2×25}{5×24}\) ]
= tan-1 [ \(\frac{5}{12}\) ]
= R.H.S. Proved.
Question 6.
Find the value of tan [ 2 tan-1 \(\frac{1}{5}\) – \(\frac { \pi }{ 4 } \) ]?
solution:

= tan tan-1( \(\frac{-7}{17}\) )
= \(\frac{-7}{17}\).
Question 7.
Prove that: 3 sin-1 x = sin-1 (3x – 4x3)? (NCERT, CBSE 2018)
Solution:
Let sin-1 x = θ
⇒ x = sin θ
We know that sin 3θ = 3 sinθ – 4 sin3 θ
= 3x – 4x3
⇒ 3θ = sin-1 ( 3x – 4x3)
⇒ 3.sin-1 x = sin-1(3x – 4x3). proved.
![]()
Question 8.
Prove that: 3 cos-1 x = cos-1 (4x3 – 3x)? (NCERT)
Solution:
Let cos-1 x = cos θ
⇒ x = cos θ
We know that cos 3θ = 4 cos3θ – 3 cos θ
= 4x3 – 3x
⇒ 3θ = cos-1 (4x3 – 3x)
⇒ 3 cos-1x = cos-1 (4x3 – 3x). Proved.
Question 9.
Prove the following:
- tan-1 \(\frac{1}{2}\) + tan-1 \(\frac{1}{3}\) = \(\frac { \pi }{ 4 } \)
- cos-1 \(\frac{12}{13}\) = tan-1 \(\frac{5}{12}\)
- cos-1 \(\frac{3}{5}\) = sin-1 \(\frac{4}{5}\)
Solution:
1. tan-1 \(\frac{1}{2}\) + tan-1 \(\frac{1}{3}\) = \(\frac { \pi }{ 4 } \)
L.H.S = tan-1 \(\frac{1}{2}\) + tan-1 \(\frac{1}{3}\)
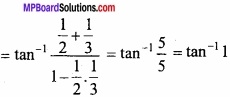
∴ A = tan-1 \(\frac{5}{12}\)
\(\frac { \pi }{ 4 } \) = R.H.S. Proved
2. cos-1 \(\frac{12}{13}\) = tan-1 \(\frac{5}{12}\)
Let cos-1 \(\frac{12}{13}\) = A
\(\frac{12}{13}\) = cos A
sin A = \(\sqrt { 1-cos^{ 2 }A } \) = \(\sqrt { 1-\frac { 144 }{ 169 } } \)
= \(\sqrt { \frac { 25 }{ 169 } } \) = \(\frac{5}{13}\)
tan A = \(\frac { sinA }{ cosA } \) = \(\frac { 5/13 }{ 12/13 } \) = \(\frac{5}{12}\)
A = tan-1 \(\frac{5}{12}\)
From eqns. (1) and (2), L.H.S = R.H.S. Proved.
3. cos-1 \(\frac{3}{5}\) = sin-1 \(\frac{4}{5}\)
Let cos-1 \(\frac{3}{5}\) = A ……………… (1)
⇒ cos A = \(\frac{3}{5}\)
⇒ sin A = \(\sqrt { 1-cos^{ 2 }A } \)
= \(\sqrt { \frac { 16 }{ 25 } } \) = \(\frac{4}{5}\) ……………… (2)
A = sin-1 \(\frac{4}{5}\).
From eqns. (1) and (2), L.H.S = R.H.S. Proved.
Question 10.
Prove that:
- sec-1 x + cosec-1 x = \(\frac { \pi }{ 2 } \)
- sin-1x + cos-1x = \(\frac { \pi }{ 2 } \)
- tan-1x + cot-1x = \(\frac { \pi }{ 2 } \)
Solution:
1. sec-1 x + cosec-1x = \(\frac { \pi }{ 2 } \)
Let sec -1 x = θ
∴x = sec θ
⇒ x = cosec ( \(\frac { \pi }{ 2 } \) – θ)
⇒ cosec -1 x = \(\frac { \pi }{ 2 } \) – θ. Proved.
2. sin-1 x + cos-1 x = \(\frac { \pi }{ 2 } \)
Let sin-1 x = θ ……………………. (1)
⇒ x = sin θ
⇒ x = cos ( \(\frac { \pi }{ 2 } \) – θ)
⇒ cos -1 x = \(\frac { \pi }{ 2 } \) – θ ………………. (2)
Adding eqns (1) and (2),
sin -1 x + cos -1 x = θ + \(\frac { \pi }{ 2 } \) – θ
⇒ sin -1 x + cos-1 x = \(\frac { \pi }{ 2 } \) Proved.
3. tan -1 x + cot-1 x = \(\frac { \pi }{ 2 } \)
Let tan -1 x = θ
⇒ x = tan θ
⇒ x = cot ( \(\frac { \pi }{ 2 } \) – θ)
⇒ cot -1 x = \(\frac { \pi }{ 2 } \) – θ
Adding eqns. (1) and (2),
tan -1 x + cot -1 x = \(\frac { \pi }{ 2 } \). Proved.
![]()
Question 11.
Prove the following:
- tan-1 5 – tan-1 3 = tan-1 \(\frac{1}{8}\)
- tan-1 3 – tan-1 2 = tan-1 \(\frac{1}{7}\)
- tan-1 7 – tan-1 5 = tan-1 3 = tan-1 \(\frac{1}{18}\)
Solution:
1. tan-1 5 – tan-1 3 = tan-1 \(\frac{1}{8}\)
L.H.S. = tan-1 5 – tan-1 3
= tan-1 \(\frac{5-3}{1+5.3}\) = tan-1 \(\frac{2}{16}\) = tan-1 \(\frac{1}{8}\)
= R.H.S. Proved.
2. Solve like Q.No. 11 (A).
3. Solve like Q.No. 11(A).
Question 12.
Prove that:
- tan-1 \(\frac{4}{7}\) – tan-1 \(\frac{1}{5}\) = tan-1 \(\frac{1}{3}\)
- tan-1 \(\frac{1}{2}\) – tan-1 \(\frac{2}{9}\) = tan-1 \(\frac{1}{4}\)
- tan-1 \(\frac{1}{7}\) + tan-1 \(\frac{1}{8}\) = tan-1 \(\frac{3}{11}\)
Solution:
1. tan-1 \(\frac{4}{7}\) – tan-1 \(\frac{1}{5}\) = tan-1 \(\frac{1}{3}\)

2. Solve like Q.No. 12 (A).
3. Solve like Q.No. 12 (A).
Question 13.
tan-1 1 + tan-1 2 + tan-1 3 = π?
Solution:
L.H.S. = tan-1 1 + (tan-1 2 + tan-1 3)
= tan-1 (1) + π + tan-1 ( \(\frac{2+3}{1-2×3}\) ),
[∵ tan-1 x + tan-1 y = π + tan-1 \(\frac{x+y}{1-xy}\), if x > 0, y > 0, xy > 1 Here xy = 6 > 1]
= tan-1 )1) + π + tan-1( \(\frac{5}{1-6}\) )
= tan-1 (1) + π + tan-1 (-1)
= tan-1 (1) + π – tan-1 (1), [∵tan-1 (-x) = – tan-1 x]
= π = R.H.S. Proved.
![]()
Question 14.
(A) If tan-1 ( \(\frac{1}{2}\) ) + tan-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \) then find the value of k?
Solution:
tan-1 ( \(\frac{1}{2}\) ) + tan-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \)

⇒ \(\frac{k+2}{2k – 1}\) = 1
⇒ k + 2 = 2k – 1
⇒2 + 1 = 2k – k
⇒ k = 3.
(B) If tan -1 ( \(\frac{1}{2}\) ) + tan-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \) then find the value of k?
Solution:
Solve like Q.No. 14 (A).
[Answer: k = -1]
(C) If tan -1 ( \(\frac{4}{5}\) ) + tan-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \) then find the value of k?
Solution:
Solve like Q.No. 14 (A).
[Answer: k = 9]
Question 15.
Prove that:
tan -1 \(\sqrt { x } \) = \(\frac{1}{2}\) cos-1 ( \(\frac{1-x}{1+x}\) )?
Solution:
R.H.S = \(\frac{1}{2}\) cos -1 ( \(\frac{1-x}{1+x}\) )
Let \(\sqrt { x } \) = tan θ
⇒ x = tan2 θ
⇒ \(\frac{1-x}{1+x}\) = \(\frac { 1-tan^{ 2 }\theta }{ 1+tan^{ 2 }\theta } \) = cos 2θ
∴ R.H.S. = \(\frac{1}{2}\) cos -1(cos 2θ)
= \(\frac{1}{2}\) × 2θ = θ
= tan-1 ( \(\sqrt { x } \) ) [∵\(\sqrt { x } \) = tan θ ⇒ tan-1 ( \(\sqrt { x } \) ) = θ]
= L.H.S. Proved.
![]()
Question 16.
Prove that:
sin (cos-1 x ) = cos (sin-1 x)?
Solution:
L.H.S. = sin(cos-1 x)
= sin [ \(\frac { \pi }{ 2 } \) – sin -1 x],
[∵ sin-1 x + cos-1x = \(\frac { \pi }{ 2 } \) , cos-1x = \(\frac { \pi }{ 2 } \) – sin-1 x]
= cos (sin-1 x), [ ∵sin (90° – θ) = cos θ ]
= R.H.S. Proved.
Question 17.
(A) Prove that:
tan-1 ( \(\frac{b-c}{1+bc}\) ) + tan-1 \(\frac{b-c}{1+bc}\) + tan-1 c = tan-1 b?
Solution:
L.H.S = tan-1 ( \(\frac{b-c}{1+bc}\) ) + tan-1 \(\frac{c-a}{1+ca}\) + tan-1 a
= (tan-1 a – tan-1 b ) + (tan-1 b – tan-1 c) + tan-1 c
= tan-1 b – tan-1 c + tan-1 c – tan-1 a + tan-1 a
= tan-1 b = R.H.S. Proved.
(B) Prove that:
tan-1 ( \(\frac{a-b}{1+ab}\) ) + tan-1 \(\frac{b-c}{1+bc}\) + tan-1 c = tan-1 a?
Solution:
L.H.S = tan-1 ( \(\frac{a-b}{1+ab}\) ) + tan-1 \(\frac{b-c}{1+bc}\) + tan-1 c
= (tan-1 a – tan-1 b) + (tan-1 b – tan-1c) + tan-1 c
= tan-1 a = R.H.S. Proved.
(C) Prove that:
tan-1 \(\frac{1}{7}\) + tan-1 \(\frac{1}{13}\) = tan-1 \(\frac{2}{9}\)?
Solution:
tan-1 \(\frac{1}{7}\) + tan-1 \(\frac{1}{13}\) = tan-1 \(\frac{2}{9}\)
L.H.S = tan-1 \(\frac{1}{7}\) + tan-1 \(\frac{1}{13}\)
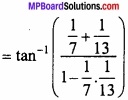
= tan-1 \(\frac{20}{91}\) × \(\frac{91}{90}\) = tan-1 \(\frac{20}{90}\) = tan-1 \(\frac{2}{9}\)
= R.H.S. Proved.
Question 18.
Solve the equation:
sin-1 \(\frac { 2a }{ 1+a^{ 2 } } \) + sin-1 \(\frac { 2b }{ 1+a^{ 2 } } \) = 2 tan-1x?
Solution:
sin-1 \(\frac { 2a }{ 1+a^{ 2 } } \) + sin-1 \(\frac { 2b }{ 1+a^{ 2 } } \) = 2 tan-1x, (given)
⇒ 2 tan-1 a + 2 tan-1 b = 2 tan-1 x [∵sin-1 \(\frac { 2x }{ 1+a^{ 2 } } \) = 2 tan-1 x]
⇒ tan-1 a + tan-1 b = tan-1 x
⇒ tan-1 \(\frac{a+b}{1-ab}\) = tan-1 x
∴ x = \(\frac{a+b}{1-ab}\).
![]()
Question 19.
solve the equation:
cos-1 ( \(\frac { 1-a^{ 2 } }{ 1+a^{ 2 } } \) ) – cos-1 ( \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) ) = 2 tan-1x?
Solution:
cos-1 ( \(\frac { 1-a^{ 2 } }{ 1+a^{ 2 } } \) ) – cos-1 ( \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) ) = 2 tan-1x, (given)
⇒ 2 tan-1 a – 2 tan-1 b = 2 tan-1 x
⇒ tan-1a – tan-1 b = tan-1 x
⇒ tan-1 \(\frac{a-b}{1+ab}\) = tan-1 x
∴ x = \(\frac{a-b}{1+ab}\).
Question 20.
(A) Prove the following:
2 tan-1 \(\frac{1}{4}\) = tan-1 \(\frac{8}{15}\)?
Solution:
∵ 2 tan-1 x = tan-1 ( \(\frac { 2x }{ 1-x^{ 2 } } \) )
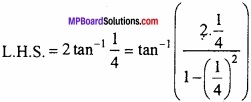
L.H.S = tan-1 \(\frac{16}{2.5}\)
= tan-1 \(\frac{8}{15}\) = R.H.S. Proved.
(B) Prove the following:
2 tan-1 \(\frac{1}{2}\) = tan-1 \(\frac{4}{3}\)?
Solution:
We know that 2 tan-1 x = tan-1 ( \(\frac { 2x }{ 1-x^{ 2 } } \) )

= tan-1 ( \(\frac{4}{3}\) )
= R.H.S. Proved.
Question 21.
Write in simplest form
tan-1 \(\sqrt { \frac { 1-cosx }{ 1+cosx } } \)?
Solution:

Question 22.
Write in simplest form:
cos-1 \(\sqrt { \frac { 1 }{ 2 } (1+cosx) } \)?
Solution:
cos-1 \(\sqrt { \frac { 1 }{ 2 } (1+cosx) } \) = cos-1 \(\sqrt { \frac { 1 }{ 2 } .2cos^{ 2 }\frac { x }{ 2 } } \)
= cos-1 (cos \(\frac{x}{2}\) ) = \(\frac{x}{2}\).
Question 23.
If tan-1 a + tan-1 b + tan-1 c = \(\frac { \pi }{ 2 } \) then prove that ab + bc + ca = 1?
Solution:
tan-1 a + tan-1 b + tan-1 c = \(\frac { \pi }{ 2 } \) , given
⇒ tan-1 a + tan-1 b + tan -1 c = tan-1 a + cot-1 a, [∵tan-1 a + cot -1 a = \(\frac { \pi }{ 2 } \) ]
⇒ tan-1 b + tan-1c = cot-1 a
⇒ tan-1 ( \(\frac{b+c}{1+bc}\) ) = \(\frac{1}{a}\)
⇒ ab + ca = 1 – bc
⇒ ab + bc + ca = 1. Proved.
![]()
Question 24.
Prove that:
tan-1 \(\frac{2}{11}\) + cot-1 \(\frac{24}{7}\) = tan-1 \(\frac{1}{2}\)?
Solution:
L.H.S. = tan-1 \(\frac{2}{11}\) + cot-1 \(\frac{7}{24}\)
= tan-1 \(\frac{2}{11}\) + tan-1 \(\frac{7}{24}\)

tan-1 = \(\frac{125}{250}\) = tan-1 \(\frac{1}{2}\) = R.H.S.
Question 25.
Prove that:
cos-1 x = 2 cos-1 \(\sqrt { \frac { 1+x }{ 2 } } \)?
Solution:
R.H.S. = 2 cos-1 \(\sqrt { \frac { 1+x }{ 2 } } \)
= 2 cos-1 \(\sqrt { \frac { 1+cos\theta }{ 2 } } \)
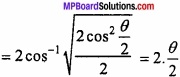
= cos-1 x
= L.H.S. Proved.
Question 26.
Prove that:
cos-1 x = 2 tan-1\(\sqrt { \frac { 1-x }{ 1+x } } \)?
Solution:
R.H.S. = 2 tan-1 \(\sqrt { \frac { 1-x }{ 1+x } } \)
= 2 tan-1 \(\sqrt { \frac { 1-cos\theta }{ 1+cos\theta } } \) (putting x = cos θ)

= 2. \(\frac { \theta }{ 2 } \) = θ = cos-1 x = L.H.S. Proved.
Question 27.
tan-1 ( \(\frac{a}{b}\) ) – tan-1 ( \(\frac{a-b}{a+b}\) ) = \(\frac { \pi }{ 4 } \)?
Solution:
tan-1 ( \(\frac{a}{b}\) ) – tan-1 ( \(\frac{a-b}{a+b}\) ) = \(\frac { \pi }{ 4 } \)

⇒ 1 = tan\(\frac { \pi }{ 4 } \)
or tan\(\frac { \pi }{ 4 } \) = 1. Proved.
Inverse Trigonometric Functions Long Answer Type Questions – I
Question 1.
(A) Prove that:
sin-1 \(\frac { 1 }{ \sqrt { 5 } } \) + sin-1 \(\frac { 1 }{ \sqrt { 10 } } \) = \(\frac { \pi }{ 4 } \)?
Solution:
Let sin-1 \(\frac { 1 }{ \sqrt { 5 } } \) = A, sin-1 \(\frac { 1 }{ \sqrt { 10 } } \) = B
∴ A + B = \(\frac { \pi }{ 4 } \)
⇒ sin (A + B) = sin\(\frac { \pi }{ 4 } \)
⇒ sin (A + B) = sin\(\frac { \pi }{ 4 } \)
⇒ sin A cos B + cos A sin B = \(\frac { 1 }{ \sqrt { 2 } } \)
L.H.S = sin A \(\sqrt { 1-sin^{ 2 }B } \) + \(\sqrt { 1-sin^{ 2 }A } \). sin B
= \(\frac { 1 }{ \sqrt { 5 } } \). \(\sqrt { 1-\frac { 1 }{ 10 } } \) + \(\sqrt { 1-\frac { 1 }{ 5 } } \). \(\frac { 1 }{ \sqrt { 10 } } \)
= \(\frac { 3 }{ \sqrt { 5.\sqrt { 10 } } } \) + \(\frac { 2 }{ \sqrt { 5.\sqrt { 10 } } } \)
= \(\frac { 5 }{ \sqrt { 5.\sqrt { 10 } } } \) = \(\sqrt { \frac { 5 }{ 10 } } \) = \(\frac { 1 }{ \sqrt { 2 } } \)
= R.H.S. Proved.
(B) Solve the following equation:
sin-1 x + sin-1 (1 – x) = sin-1 \(\sqrt { 1-x^{ 2 } } \)?
Solution:
Let sin-1 x = α ∴ x = sin α
Here α + sin-1 ( 1 – sin α) = sin-1 \(\sqrt { 1-sin^{ 2 }\alpha } \)
⇒ α + sin-1 ( 1 – sin α) = sin-1 cos α
⇒ α + sin-1 ( 1 – sin α) = sin-1. sin ( \(\frac { \pi }{ 2 } \) – α)
⇒ α + sin-1 ( 1 – sin α) = \(\frac { \pi }{ 2 } \) – α
⇒ sin-1 ( 1 – sin α) = \(\frac { \pi }{ 2 } \) – 2α
⇒ 1 – sin α = sin ( \(\frac { \pi }{ 2 } \) – 2α)
⇒ 1 – sin α = cos 2α
⇒ 1 – cos 2α = sin α
⇒ 2 sin2α = sin α
⇒ sin α = \(\frac{1}{2}\) ∴α = \(\frac { \pi }{ 6 } \)
or x = \(\frac { \pi }{ 6 } \)
![]()
Question 2.
- tan-1 \(\frac{x+1}{x}\) – tan-1 \(\frac{1}{2x+1}\) = \(\frac { \pi }{ 4 } \)?
- If tan-1 x + tan-1 y + tan-1 z = π then prove that x + y + z = xyz?
- If tan-1 x + tan-1 y + tan-1 z = \(\frac { \pi }{ 2 } \) then prove that xy + yz + zx = 1?
Solution:
1. tan-1 \(\frac{x+1}{x}\) – tan-1 \(\frac{1}{2x+1}\) = \(\frac { \pi }{ 4 } \)

= R.H.S.
2. tan-1 x + tan-1 y + tan-1 z = π
⇒ tan-1 \(\frac{x+y}{1-xy}\) + tan-1 z = π
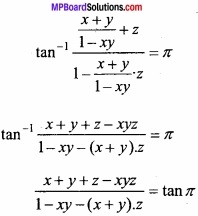
⇒ x + y + z – xyz = 0, [∵ tan π = 0]
∴ x + y + z = xyz. Proved.
3. Solve like Q.2(B), take tan \(\frac { \pi }{ 4 } \) = ∞ = \(\frac{1}{0}\)
Question 3.
Write in simplest form:
tan-1 [ \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) ]?
Solution:
tan-1 [ \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) ]
Let x = tan θ

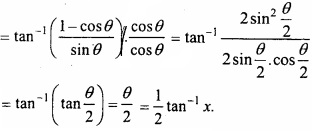
Question 4.
(A) Prove the following:
\(\frac{1}{2}\) sin-1 x = cot-1 [ \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) ]?
Solution:
R.H.S = cot-1 [ \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) ]
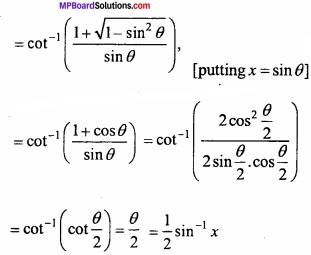
= L.H.S. Proved.
(B) Prove that:
\(\frac{1}{2}\) cot-1 x = cot-1 ( \(\sqrt { 1+x^{ 2 }+x } \) )?
Solution:
\(\frac{1}{2}\) cot-1 x = cot-1 ( \(\sqrt { 1+x^{ 2 }+x } \) )
R.H.S = cot-1 ( \(\sqrt { 1+x^{ 2 }+x } \) )
Let x = cos θ
R.H.S = cot-1 ( \(\sqrt { 1+cot^{ 2 }\theta } \) + cot θ )
= cot-1 ( \(\sqrt { cosec^{ 2 }\theta } \) + cot θ )
= cot-1 (cosec θ + cot θ)
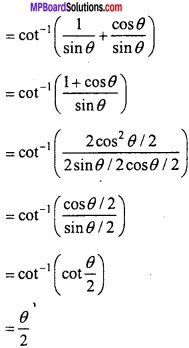
= \(\frac{1}{2}\) cot-1 x
= L.H.S. Proved.
Question 5.
Solve the following equation:
tan-1 (x + 1) + tan-1 (x – 1) = tan-1 ( \(\frac{6}{17}\) )?
Solution:
Given: tan-1 (x + 1) + tan-1 (x – 1) = tan-1 ( \(\frac{6}{17}\) )
⇒ tan-1 (x + 1) + tan-1 (x – 1) = tan-1 ( \(\frac{6}{17}\) )
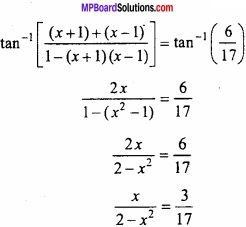
⇒ 17 x = 6 – 3x2
⇒ 3x2 + 17x – 6 = 0
⇒ 3x2 + 18x – x – 6 = 0
⇒ 3x (x + 6) – 1 (x + 6) = 0
⇒ (x+6) (3x – 1) = 0
∴ x = – 6, x = \(\frac{1}{3}\)
![]()
Question 6.
Prove that cos-1 \(\frac{3}{5}\) + cos-1 \(\frac{4}{5}\) = \(\frac { \pi }{ 2 } \)?
Solution:
L.H.S = cos-1 \(\frac{3}{5}\) + cos-1 \(\frac{4}{5}\),
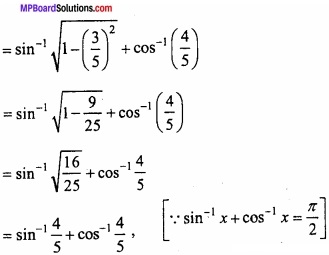
= \(\frac { \pi }{ 2 } \) = R.H.S Proved.
Question 7.
If cos-1 x + cos-1 y + cos-1 z = π then prove that:
x2 + y2 + z2 + 2xyz = 1?
Solution:
Given: cos-1 x + cos-1 z = π
⇒ cos-1 x + cos-1 y = π- cos-1 z

Squaring on both sides
x2y2 + z2 + 2xyz = (1 – x2) (1 – y2)
⇒ x2y2 + z2 + 2xyz = 1 – y2 – x2 + x2y2
⇒ z2 + 2xyz = 1 – y2 – x2
⇒ x2 + y2 + z2 + 2xyz = 1. Proved.
Question 8.
If sin-1 \(\frac { 2a }{ 1+a^{ 2 } } \) – cos-1 \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) = tan-1 \(\frac { 2x }{ 1-x^{ 2 } } \) then prove that:
x = \(\frac{a-b}{1+ab}\)?
Solution:
![]()
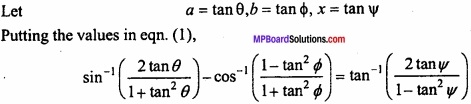
⇒ sin-1 (sin 2θ) – cos-1 (cos 2ϕ) = tan-1 (tan 2Ψ)
⇒ 2θ – 2ϕ = 2Ψ
⇒ θ – ϕ = Ψ
⇒ tan-1 a – tan-1 b = tan-1 x
⇒ tan-1 ( \(\frac{a-b}{1+ab}\) ) = tan-1 x
⇒ x = \(\frac{a-b}{1+ab}\). Proved.
Question 9.
Prove the following

Solution:
Let x = cos θ, then θ = cos-1 x.
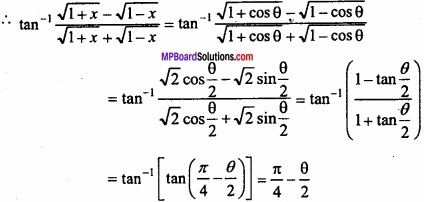
\(\frac { \pi }{ 4 } \) – \(\frac{1}{2}\) cos-1 x.
Question 10.
Write in simplest form:
tan-1 ( \(\frac { x }{ \sqrt { 1+x^{ 2 }-1 } } \) )?
Solution:
tan-1 ( \(\frac { x }{ \sqrt { 1+x^{ 2 }-1 } } \) )
Putting x = tan θ, we get
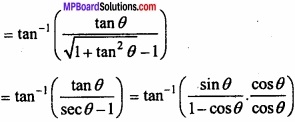
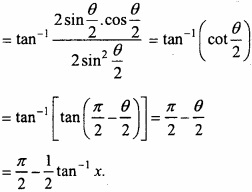
Question 11.
Prove that:
tan-1 \(\sqrt{x}\) = \(\frac{1}{2}\) cos-1 ( \(\frac{1-x}{1+x}\) )? (NCERT)
Solution:
tan-1 \(\sqrt{x}\) = \(\frac{1}{2}\) cos-1 ( \(\frac{1-x}{1+x}\) )
R.H.S = \(\frac{1}{2}\) cos-1 ( \(\frac{1-x}{1+x}\) )
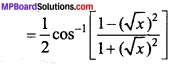
Let tan-1 \(\sqrt{x}\) = θ
\(\sqrt{x}\) = tan θ
R.H.S. = \(\frac{1}{2}\) cos-1(cos 2θ)
= \(\frac{1}{2}\). 2θ
= θ
= tan-1 \(\sqrt{x}\)
= L.H.S. Proved.
![]()
Question 12.
Prove that:
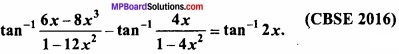
Solution:

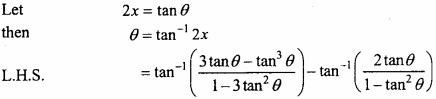
= tan-1 (tan 3θ) – tan-1 (tan 2θ)
= 3θ – 2θ
= θ
= tan-1 2x
= R.H.S. Proved.
Question 13.
Prove that:
cos-1 \(\frac{4}{5}\) + cos-1 \(\frac{12}{13}\) = cos-1 \(\frac{33}{65}\)?
Solution:
Let cos-1 \(\frac{4}{5}\) = A
∴ \(\frac{4}{5}\) = cos A
∴ sin A = \(\sqrt { 1-cos^{ 2 }A } \) = \(\sqrt { 1-\frac { 16 }{ 25 } } \) = \(\sqrt { \frac { 9 }{ 25 } } \)
⇒ sin A = \(\frac{3}{5}\)
Let cos-1 \(\frac{12}{13}\) = B
⇒ \(\frac{12}{13}\) = B
∴ sin B = \(\sqrt { 1-cos^{ 2 }B } \) = \(\sqrt { 1-\frac { 144 }{ 169 } } \) = \(\sqrt { \frac { 25 }{ 169 } } \)
⇒ sin B = \(\frac{5}{13}\)
A + B = cos-1 \(\frac{33}{65}\)
⇒ cos (A + B) = \(\frac{33}{65}\)
⇒ cos A.cos B – sin A.sin B = \(\frac{33}{65}\)
L.H.S. = \(\frac{4}{5}\). \(\frac{12}{13}\) – \(\frac{3}{5}\). \(\frac{5}{13}\)
= \(\frac{48}{65}\) – \(\frac{15}{65}\)
= \(\frac{33}{65}\)
= R.H.S. Proved.