MP Board Class 12th Maths Book Solutions Chapter 13 प्रायिकता विविध प्रश्नावली

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 13 प्रायिकता विविध प्रश्नावली Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 13 प्रायिकता विविध प्रश्नावली

प्रश्न 1.
A और B इस प्रकार घटनाएँ हैं कि P(A) ≠ 0.
p\(\left(\frac{\boldsymbol{B}}{\boldsymbol{A}}\right)\) ज्ञात कीजिए यदि
(i) A, समुच्चय B का उपसमुच्चय है।
(ii) A ∩ B = ϕ
हल:
(i) B का उपसमुच्चय A है।

प्रश्न 2.
एक दम्पति के दो बच्चे हैं–
(i) दोनों बच्चों के लड़का होने की प्रायिकता ज्ञात कीजिए यदि यह ज्ञात है कि दोनों बच्चों में से कम-से-कम एक बच्चा लड़का है।
(ii) दोनों बच्चों के लड़की होने की प्रायिकता ज्ञात कीजिए यदि यह ज्ञात है कि बड़ा बच्चा लड़की है।
हल:
(i) माना A = दोनों बच्चे लड़के हैं = {MM}
B = कम-से-कम एक बच्चा लड़का है
={MF, FM, MM }

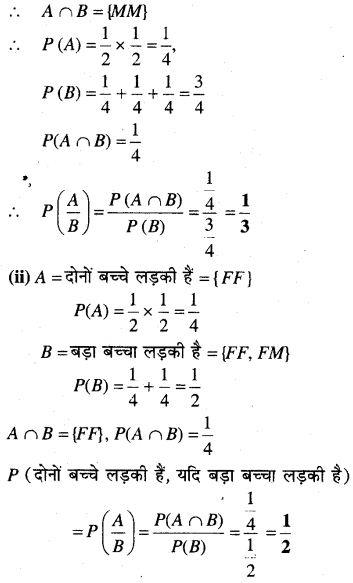
प्रश्न 3.
कल्पना कीजिए कि 5% पुरुषों और 0.25% महिलाओं के बाल सफेद हैं। एक सफेद बालों वाले व्यक्ति को यादृच्छिक चुना गया है। इस व्यक्ति के पुरुष होने की प्रायिकता क्या है? यह मान लें कि पुरुषों और महिलाओं की संख्या समान है।
हल:
माना घटना E₁ – पुरुष का होना तथा घटना
E₂ – महिला का होना
तथा घटना A – सफेद बाल का होना
∴ 1 पुरुष चुनने की प्रायिकता = P (E₁) = \(\frac{1}{2}\)
1 महिला चुनने की प्रायिकता = P (E₂) = \(\frac{1}{2}\)
5% पुरुषों के बाल सफेद हैं
∴ P\(\left(\frac{A}{E_{1}}\right)\) = 5% = 0.05
∵ 0.25% महिलाओं के बाल सफेद हैं
∴ P\(\left(\frac{A}{E_{2}}\right)\) = 0.25% = 0.0025
इसलिए सफेद बालों वाला पुरुष होने की प्रायिकता

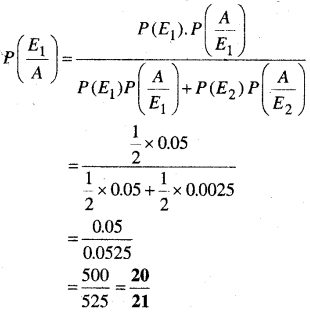
प्रश्न 4.
मान लीजिए कि 90% लोग दाहिने हाथ से काम करने वाले हैं। इसकी प्रायिकता क्या है कि 10 लोगों में से यादृच्छया चुने गए अधिक-से-अधिक 6 लोग दाहिने हाथ से काम करने वाले हों?
हल : 90% लोग दाहिने हाथ से काम करते हैं।
p = \(\frac{9}{10}\)
10% लोग बायें हाथ से काम करते हैं।
q = \(\frac{1}{10}\), n = 10
P (अधिक-से-अधिक 6 लोग दाहिने हाथ से काम करने वाले हों)
= p(O) + p (1) +…+ p (6)

प्रश्न 5.
एक कलश (पात्र) में 25 गेंदें हैं, जिनमें से 10 गेंदों पर चिन्ह ‘x’ अंकित है और शेष 15 पर चिन्ह ‘Y’ अंकित है। कलश में से एक गेंद यादृच्छया निकाली जाती है और उस पर अंकित चिन्ह को नोट (लिख) करके उसे कलश में तिस्थापित कर दिया जाता है। यदि इस प्रकार से 6 गेंदें नेकाली जाती हों तो निम्नलिखित प्रायिकताएँ ज्ञात कीजिए।
(i) सभी पर चिन्ह ‘X’ अंकित हो।
(ii) 2 से अधिक पर चिन्ह ‘Y’ नहीं अंकित हो।
(iii) कम-से-कम 1 गेंद पर चिन्ह ‘Y’ अंकित हो।
(iv) ‘x’ तथा ‘x’ चिन्हों से अंकित गेंदों की संख्याएँ नमान हों।
हल:
गेंदों की कुल संख्या = 25
X अंकित गेंदों की संख्या =10
माना X अंकित गेंदों की घटना X से व्यक्त करते हैं।
Y = Y गेंद की घटना
∴ P(X) = \(\frac{10}{25}=\frac{2}{5}\) = P
∴ P(Y) = \(1-\frac{2}{5}=\frac{3}{5}\) = q
अब 6 गेंद खींचते हैं।
(i) P (सभी पर चिन्ह X अंकित हो) = \(\left(\frac{2}{5}\right)^{6}\)
(ii) P (2 0से अधिक पर चिन्ह Y नहीं अंकित हो)
= P (6) + P (5) + P (4)

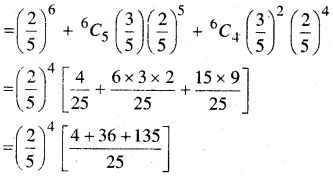
= \(\left(\frac{2}{5}\right)^{4}\left[\frac{175}{25}\right]=7\left(\frac{2}{5}\right)^{4}\)
(iii) P (कम-से-कम 1 गेंद पर चिन्ह Y अंकित हो)
= 1 – (चिन्ह Y अंकित न हो)
= 1 – P (सभी गेंदों पर x अंकित हो)
= 1 – \(\left(\frac{2}{5}\right)^{6}\)
(iv) P(X तथा Y चिन्हों से अंकित गेंदों की संख्याएँ समान हों)

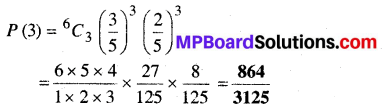
प्रश्न 6.
एक बाधा दौड़ में एक प्रतियोगी को 10 बाधाएँ पार करनी हैं। इसकी प्रायिकता कि वह प्रत्येक बाधा को पार कर \(\frac{5}{6}\) लेगा है। इसकी क्या प्रायिकता है कि वह 2 से कम बाधाओं को गिरा देगा (नहीं पार कर पाएगा)?
हल:
दौड़ प्रतियोगिता में कुल बाधाएँ = 10
∵ बाधा को पार करने की प्रायिकता = \(\frac{5}{6}\)
∴ बाधा को पार न करने की प्रायिकता = \(1-\frac{5}{6}=\frac{1}{6}\)
अतः 2 से कम बाधाओं को गिराने की प्रायिकता
= P (10) + P (2)

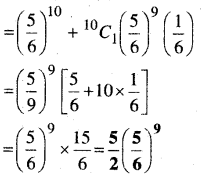
प्रश्न 7.
एक पासे को बार-बार तब तक उछाला जाता है जब तक कि उस पर 6 का अंक तीन बार प्राप्त नहीं हो जाता। इसकी प्रायिकता ज्ञात कीजिए कि पासे पर तीसरा 6 का अंक उसे छठी बार उछालने पर प्राप्त होता है।
हल:
एक पासे को बार-बार उछाला जाता है।
एक उछाल में 6 का अंक आने की प्रायिकता = \(\frac{1}{6}\)
एक उछाल में 6 का अंक न आने की प्रायिकता
= \(1-\frac{1}{6}=\frac{5}{6}\)
पासे पर 5 उछालों पर 2. बार 6 और 3 बार 6 न आने की प्रायिकता
= ⁵C₂
छठी बार उछालने में 6 आने की प्रायिकता = \(\frac{1}{6}\)
∴ पासे पर तीसरा 6 का अंक उसे छठी बार उछालने पर प्राप्त प्रायिकता

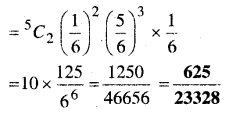
प्रश्न 8.
यदि एक लीप वर्ष को यादृच्छया चुना गया हो तो इसकी क्या प्रायिकता है कि उस वर्ष में 53 मंगलवार होंगे।
हल:
∵ एक लीप वर्ष में होते हैं = 366 दिन
अर्थात् 52 सप्ताह तथा 2 दिन (अलग से)
अतिरिक्त दो दिन हो सकते हैं
= (Mon, Tue), (Tue, Wed), (Wed, Thu), (Thu, Fri), (Fri, Sat), (Sat, Sun), (Sun, Mon)
सम्भावित परिणाम = 7
अनुकूल परिणाम = 2 (Mon, Tue) (Tue, Wed)
अतः 53 मंगलवार होने की प्रायिकता = \(\frac{2}{7}\)

प्रश्न 9.
एक प्रयोग के सफल होने का संयोग उसके असफल होने से दो गुना है। प्रायिकता ज्ञात कीजिए कि अगले छः परीक्षणों में कम-से-कम 4 सफल होंगे।
हल:
माना सफल होने की प्रायिकता p तथा असफल होने की प्रायिकता q है।
एक प्रयोग के सफल होने का संयोग उसके असफल होने से दो गुना है।
⇒ p = 2q = 2 (1 – p) = 2 – 2p
∴ 3p = 2 या p = \(\frac{2}{3}\)
∴ q = \(\frac{1}{3}\)
अगले छ: परीक्षणों में कम-से-कम 4 सफल होने की प्रायिकता
= P(4) + P(5) + P(6)

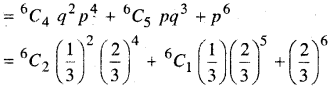
प्रश्न 10.
एक व्यक्ति एक न्याय्य सिक्के को कितनी बार उछाले कि कम-से-कम एक चित की प्रायिकता 90% से अधिक हो?
हल:
माना सिक्के को x बार उछाला गया है।
चित आने की प्रायिकता = \(\frac{1}{2}\)
तथा चित न आने की प्रायिकता = \(\left(\frac{1}{2}\right)^{n}\)
∴ कम-से-कम एक चित आने की प्रायिकता = \(1-\left(\frac{1}{2}\right)^{n}\)
इसलिए हम कम-से-कम एक चित की प्रायिकता ज्ञात करेंगे जो कि 90% (0.9) से अधिक हो।
अतः कम-से-कम एक चित आने की प्रायिकता > 0.9

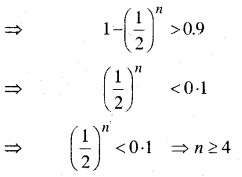
अतः एक न्याय्य सिक्के को कम-से-कम 4 बार उछालना पड़ेगा।

प्रश्न 11.
एक खेल में किसी व्यक्ति को एक न्याय्य पासे को उछालने के बाद छः प्रकट होने पर एक रुपया मिलता है और अन्य कोई संख्या प्रकट होने पर वह एक रुपया हार जाता है। एक व्यक्ति यह निर्णय लेता है कि वह पासे को तीन बार फेंकेगा लेकिन जब भी छः प्राप्त होगा वह खेलना छोड़ देगा। उसके द्वारा जीती/हारी गई राशि की प्रत्याशा ज्ञात कीजिए।
हल:
जब पासे को उछालते हैं, तब 6 प्रकट होने की प्रायिकता
= \(\frac{1}{6}\) = p (माना)
∴ q = \(1-\frac{1}{6}=\frac{5}{6}\)
(i) छ: प्रकट होने की प्रायिकता = \(\frac{1}{6}\)
(ii) पहली उछाल में 6 प्रकट न हो किन्तु दूसरी उछाल में 6 प्रकट होने की प्रायिकता
= \(\frac{5}{6} \times \frac{1}{6}=\frac{5}{36}\)
पहली दो उछाल में 6 न प्रकट होने की तथा तीसरी उछाल में 6 प्रकट होने की प्रायिकता
= \(\frac{5}{6} \times \frac{5}{6} \times \frac{1}{6}=\frac{25}{216}\)
तीनों उछालों में 6 न प्रकट होने की प्रायिकता
= \(\left(\frac{5}{6}\right)^{3}=\frac{125}{216}\)
पहली उछाल में 6 प्रकट होने पर एक रुपया मिलता है।
दूसरी उछाल में 6 प्रकट होने पर (1 – 1) रुपये = 0 रुपये मिलते हैं।
तीसरी उछाल में 6 प्रकट होने पर प्राप्त होता है
= ( – 1 – 1 + 1) रुपये
=( – 1) Rs. = 1 रुपया कम

प्रश्न 12.
मान लीजिए हमारे पास A, B, Cऔर D बक्से हैं जिसमें रखी संगमरमर की लाल, सफेद और काली टुकड़ियों का विवरण निम्न तरीके से है यादृच्छया एक बॉक्स चुना जाता है तथा इससे एक टुकड़ा निकाला जाता है। यदि टुकड़ा लाल हो तो इसे बॉक्स A; बॉक्स B, बॉक्स C से निकाले जाने की क्या प्रायिकता है?

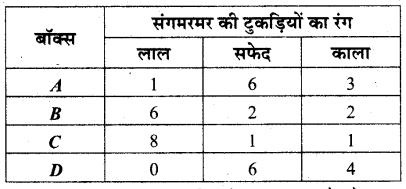
हल:
माना एक बॉक्स चुने जाने की घटना F है और लाल गेंद चुनने की घटना A है।

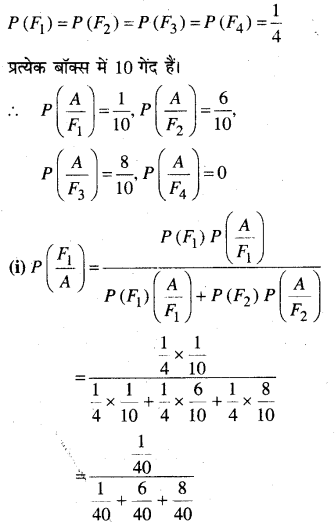
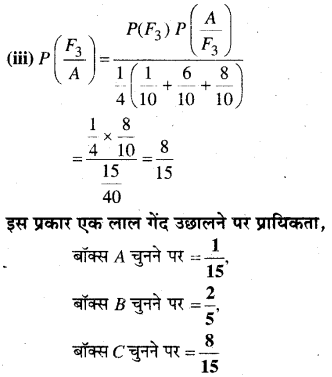
प्रश्न 13.
मान लीजिए किसी रोगी को दिल का दौरा पड़ने का संयोग 40% है। यह मान लिया जाता है कि ध्यान ओर योग विधि दिल का दौरा पड़ने के खतरे को 30% कम कर देता है और दवा द्वारा खतरे को 25% कम किया जा सकता है। किसी भी समय रोगी इन दोनों में से किसी एक विकल्प का चयन करता है। यह दिया गया है कि उपरोक्त विकल्पों से किसी एक का चुनाव करने वाले रोगियों से यादृच्छया चुना गया रोगी दिल के दौरे से ग्रसित हो जाता है। रोगी द्वारा ध्यान और योग विधि का उपयोग किए जाने की प्रायिकता ज्ञात कीजिए।
हल:
माना E₁ = ध्यान और योग विधि का इलाज
E₂ = दवा द्वारा खतरे को कम किए जाने का इलाज
A = दिल के दौरे से रोगी
P(E₁) =\(\frac{1}{2}\), P(E₂) = \(\frac{1}{2}\)
माना P(A) = 40% = 0.40
दवा द्वारा दिल का दौरा पड़ने का 25% खतरा कम हो जाता है।
⇒ दवा द्वारा दिल का दौरा पड़ने से खतरा 75% है।

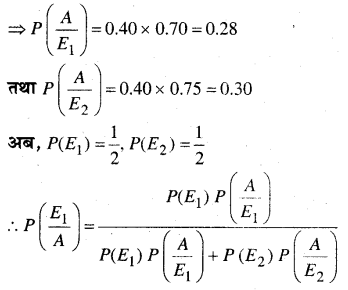
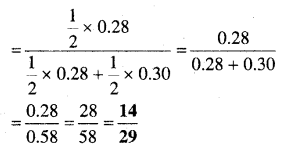
प्रश्न 14.
यदि 2 कोटि के एक सारणिक के सभी अवयव शून्य या एक हों तो सारणिक का धनात्मक मान होने की क्या प्रायिकता है। (मान लीजिए कि सारणिक के प्रत्येक अवयव स्वतन्त्र रूप से चुने जा सकते हैं तथा प्रत्येक की चुने जाने की प्रायिकता 1 है।)
हल:
यहाँ 2 कोटि के सारणिक में चार अवयव हैं।
∴ सारणिकों द्वारा बनाई गई संख्या = 2⁴ =16
सारणिक का मान धनात्मक है।

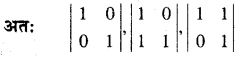
सारणिक का धनात्मक मान होने की प्रायिकता = \(\frac{3}{16}\)

प्रश्न 15.
एक इलेक्ट्रॉनिक एसेंबली के दो सहायक निकाय A और B हैं। पूर्ववर्ती निरीक्षण द्वारा निम्न प्रायिकताएँ ज्ञात हैं
P(A के असफल होने की) = 0.2
P(B के अकेले असफल होने की) = 0.15
P(A और B के असफल होने की) = 0.15
तो, निम्न प्रायिकताएँ ज्ञात कीजिए
(i) P(A असफल / B असफल हो चुकी हो)
(ii) P(A के अकेले असफल होने की)
हल:

= 0.20 – 0.15 = 0.05

प्रश्न 16.
थैला I में 3 लाल तथा 4 काली गेंदें हैं तथा थैला II में 4 लाल और 5 काली गेंदें हैं। एक गेंद को थैला 1 से थैला II में स्थानान्तरित किया जाता है और तब एक गेंद थैला II से निकाली जाती है। निकाली गई गेंद लाल रंग की है। स्थानान्तरित गेंद की काली होने की प्रायिकता ज्ञात कीजिए।
हल:
थैला I में 3 लाल तथा 4 काली गेंदें हैं।
थैला II में 4 लाल तथा 5 काली गेंदें हैं।
माना E₁ = थैला I में लाल गेंद निकालने की घटना।
E₂ = थैला I में काली गेंद निकालने की घटना
∴ P(E₁) = \(\frac{3}{7}\), P(E₂) = \(\frac{4}{7}\)
माना लाल गेंद निकालने की घटना A है।

निम्नलिखित प्रश्नों में सही उत्तर का चुनाव कीजिए-
प्रश्न 17.
यदि A और B दो ऐसी घटनाएँ हैं कि P(A) ≠ 0 और P\(\left(\frac{\boldsymbol{B}}{\boldsymbol{A}}\right)\) = 1, तब
(A) A ⊂ B
(B) B ⊂ A
(C) B = ϕ
(D) A = ϕ
हल:
P\(\left(\frac{\boldsymbol{B}}{\boldsymbol{A}}\right)\) = 1v

प्रश्न 18.
यदि P\(\left(\frac{\boldsymbol{A}}{\boldsymbol{B}}\right)\) > P(A), तब निम्न में से कौन सही है।
(A) P \(\left(\frac{\boldsymbol{B}}{\boldsymbol{A}}\right)\) < P(B)
(B) P(A ∩ B) < P (A). P (B) (C) P\(\left(\frac{\boldsymbol{B}}{\boldsymbol{A}}\right)\) > P(B)
(D) P\(\left(\frac{\boldsymbol{B}}{\boldsymbol{A}}\right)\) = P(B)
हल:

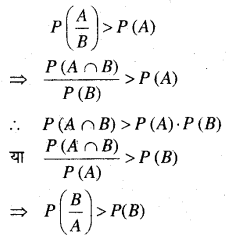
अतः विकल्प (C) सही है।

प्रश्न 19.
यदि A और B ऐसी दो घटनाएँ हैं कि P(A) + P (B) – P(A और B) = P(A), तब

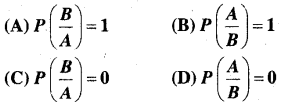
हल:
P (A) + P (B) – P(A ∩ B) = P (A)
⇒ P(B) – P (A ∩ B) = 0
या P(A ∩ B) = P (B)

अतः विकल्प (B) सही है।