MP Board Class 11th Physics Important Questions Chapter 3 सरल रेखा में गति

Students get through the MP Board Class 11th Physics Important Questions Chapter 3 सरल रेखा में गति which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 3 सरल रेखा में गति

अति लघु उत्तरीय प्रश्न

प्रश्न 1.
बिन्दु वस्तु से क्या तात्पर्य है ? उदाहरण सहित समझाइये।
उत्तर-
यदि वस्तु द्वारा चली गयी दूरी, उसके आकार की तुलना में बहुत अधिक हो तो वस्तु को बिन्दु वस्तु माना जाता है।

प्रश्न 2.
एकविमीय गति को उदाहरण सहित समझाइये।
उत्तर-
एकविमीय गति-जब कोई वस्तु सरल रेखा में गति करती है तो उसकी गति को एकविमीय गति कहते हैं। उदाहरण-सीधी सड़क पर कार की गति।

प्रश्न 3.
विस्थापन एवं दूरी को परिभाषित कीजिए।
उत्तर-
विस्थापन-किसी वस्तु की प्रारंभिक एवं अंतिम स्थिति के मध्य की न्यूनतम दूरी को विस्थापन कहते हैं।
दूरी-दिये गये समयान्तराल में किसी वस्तु द्वारा तय किये गये पथ की लंबाई को दूरी कहते हैं।

प्रश्न 4.
वस्तु की गति की दिशा वेग या त्वरण किससे निर्धारित होती है ?
उत्तर-वेग से।

प्रश्न 5.
वेग किसे कहते हैं ? इसका SI में मात्रक लिखिए।
उत्तर-
किसी गतिशील वस्तु के विस्थापन की दर (अर्थात् निश्चित दिशा में 1 सेकण्ड में चली गई दूरी) को उसका वेग कहते हैं।

इसका SI मात्रक मीटर/सेकण्ड है। यह एक सदिश राशि है।

प्रश्न 6.
चाल किसे कहते हैं ? इसका SI मात्रक लिखिए।
उत्तर-
किसी गतिशील वस्तु की स्थिति परिवर्तन की दर (अर्थात् 1 सेकण्ड में चली गई दूरी) को उसकी चाल कहते हैं।

इसका SI मात्रक मीटर/सेकण्ड है। यह एक अदिश राशि है।

प्रश्न 7.
आपेक्षिक वेग से आप क्या समझते हैं ?
अथवा
आपेक्षिक वेग का अर्थ स्पष्ट कीजिए।
उत्तर-
आपेक्षिक वेग-किसी वस्तु के सापेक्ष दूसरी वस्तु का आपेक्षिक वेग वह दर है जिससे कि पहली वस्तु के सापेक्ष दूसरी वस्तु की स्थिति बदलती है।
यदि वस्तु A और B के वेग क्रमशःv₁ और v₂ हों
तो A के सापेक्ष B का आपेक्षिक वेग = v₂– v₁
तथा B के सापेक्ष A का आपेक्षिक वेग = v₁– v₂.

प्रश्न 8.
त्वरण से आप क्या समझते है ? इसका SI मात्रक लिखिए।
उत्तर-
वेग परिवर्तन की दर को त्वरण कहते हैं। इसका SI मात्रक m/s² है।

प्रश्न 9.
एक पिण्ड का वेग नियत है तब इसमें त्वरण होगा?
उत्तर-
शून्य।

प्रश्न 10.
किसी बंदूक द्वारा ऊपर की ओर दागी गयी गोली कुछ समय बाद उसी स्थान पर लौट आती है, गोली का विस्थापन कितना है ?
उत्तर-
गोली का विस्थापन शून्य होगा।

प्रश्न 11.
कारण सहित बताइये कि क्या किसी पिण्ड की गति में त्वरण हो सकता है यदि
(i) वह एकसमान चाल से गतिमान हो? उत्तर-हाँ, क्योंकि चाल समान होते हुए भी गति की दिशा में परिवर्तन हो सकता है।
(ii) वह एकसमान वेग से गतिमान हो ?
उत्तर-
नहीं, क्योंकि वेग परिवर्तन की दर को त्वरण कहते हैं।

प्रश्न 12.
यदि किसी पिण्ड का विस्थापन, समय के वर्ग के समानुपाती है तो पिण्ड एकसमान वेग से चल रहा है या एकसमान त्वरण से ?
उत्तर-
यदि पिण्ड का विस्थापन, समय के वर्ग के अनुक्रमानुपाती होता है तो पिण्ड एकसमान त्वरण से चलता है।

प्रश्न 13.
एक गोली किसी मीनार की चोटी से u वेग से ऊपर की ओर फेंकी जाती है, उसके पश्चात् एक दूसरी गोली, उसी प्रारंभिक वेग से ठीक नीचे की ओर फेंकी जाती है। यदि वायु का प्रतिरोध नगण्य हो तो पृथ्वी से टकराते समय किस गोली का वेग अधिक होगा?
उत्तर-
पहली गोली जब ऊपर जाकर लौटती है तो मीनार की चोटी के तल में आने पर उसका वेग भी नीचे की दिशा में u हो जाता है, अत: दोनों गोलियाँ एकसमान वेग से जमीन पर टकरायेंगी।

प्रश्न 14.
क्या किसी वस्तु का औसत वेग शून्य परन्तु औसत चाल शून्य नहीं हो सकती है?
उत्तर-
यदि एक पिण्ड को ऊर्ध्वाधर ऊपर की ओर फेंका जाये तथा वह अपने प्रारंभिक स्थान पर लौट आये तो उसका औसत वेग शून्य होगा लेकिन औसंत चाल शून्य नहीं होगी, लेकिन इसका विपरीत संभव नहीं

प्रश्न 15.
क्या ऐसा संभव है कि किसी वस्तु की चाल स्थिर हो लेकिन वेग परिवर्तनशील हो?
उत्तर-
किसी कण की एकसमान वृत्तीय गति में ऐसा संभव है।

प्रश्न 16.
क्या किसी वस्तु का वेग स्थिर लैकिन चाल परिवर्तनशील हो सकती है?
उत्तर-
वस्तु का वेग स्थिर होने पर वेग का परिमाण अर्थात् वस्तु की चाल तथा दिशा दोनों नियत रहती हैं, अत: ऐसा संभव नहीं है।

प्रश्न 17.
समरूप गति के लिए वेग-समय ग्राफ खींचिए।
उत्तर:

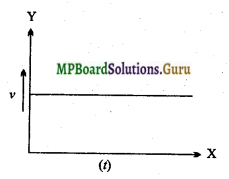
प्रश्न 18.
एकसमान त्वरित गति के लिए वेग-समय ग्राफ खींचिए। इसके ढाल से हमें क्या प्राप्त होता है ?
उत्तर-

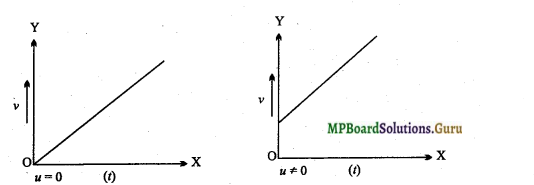
इसके ढाल से हमें त्वरण प्राप्त होता है।

प्रश्न 19.
स्थिति-समय ग्राफ का ढाल क्या प्रदर्शित करता है ?
उत्तर-
स्थिति-समय ग्राफ का ढाल वेग को प्रदर्शित करता है।

प्रश्न 20.
किन्हीं दो क्षणों के मध्य खींचे गये वेग-समय ग्राफ के अंतर्गत आने वाला क्षेत्रफल क्या प्रदर्शित करता है ?
उत्तर-
वस्तु के विस्थापन को प्रदर्शित करता है।

 

लघु उत्तरीय प्रश्न

प्रश्न 1.
विस्थापन और दूरी में अन्तर लिखिए।
उत्तर-
विस्थापन और दूरी में अन्तर

विस्थापन	दूरी
1. यह दिये गये समयान्तराल में वस्तु के स्थिति निर्देशांकों के अन्तर के तुल्य होता है। |	1. यह दिये गये समयान्तराल में वस्तु द्वारा तय किये गये पथ की लम्बाई के तुल्य होती है।
2. यह एक सदिश राशि है।	2. यह एक अदिश राशि है।
3. विस्थापन धनात्मक, ऋणात्मक या शून्य हो सकता है।	3. दूरी सदैव धनात्मक होती है।
4. विस्थापन वस्तु के पथ की प्रकृति पर निर्भर नहीं करता।	4. दूरी वस्तु के पथ की प्रकृति पर निर्भर करती है।

प्रश्न 2.
वेग और चाल में अन्तर लिखिए।
उत्तर-
वेग और चाल में अन्तर

वेग	चाल
1. किसी निश्चित दिशा में इकाई समय में गतिशील वस्तु द्वारा तय की गई दूरी को उस वस्तु का वेग कहते हैं।	1. इकाई समय में – गतिशील वस्तु द्वारा तय की गई दूरी को उस वस्तु की चाल कहते हैं।
2. वेग एक सदिश राशि है।	2. चाल एक अदिश राशि है।
3. वेग धनात्मक, ऋणात्मक या शून्य हो सकता है।	3. चाल सदैव धनात्मक होती है।

प्रश्न 3.
एकसमान वेग तथा एकसमान चाल में अन्तर लिखिए।
उत्तर-
जब समान समयान्तराल में किसी वस्तु का विस्थापन समान होता है, चाहे समयान्तराल कितना भी छोटा क्यों न हो, तो उसके वेग को एकसमान वेग कहते हैं।
जब कोई वस्तु समान समयान्तराल में समान दूरी तय करती है, चाहे समयान्तराल कितना भी छोटा क्यों न हो, तो उसकी चाल को एकसमान चाल कहते हैं।

प्रश्न 4.
नीचे दिये गये गति के कौन-से उदाहरणों में वस्तु को बिन्दु वस्तु माना जा सकता है
(a) दो स्टेशनों के मध्य बिना किसी झटके के चल रही कोई रेलगाडी।
(b) किसी वृत्तीय पथ पर साइकिल चला रहे किसी व्यक्ति के ऊपर बैठा कोई बन्दर।
(c) जमीन से टकरा कर तेजी से मुड़ने वाली क्रिकेट की कोई फिरकती गेंद।
(d) किसी मेज के किनारे से फिसलकर गिरा कोई बीकर।
उत्तर-
(a) एवं
(b) स्थितियों में वस्तु को बिन्दु आकार माना जा सकता है, क्योंकि रेलगाड़ी द्वारा तय की गई दूरी उसके आकार की तुलना में अधिक है। इसी प्रकार वृत्तीय पथ पर बंदर द्वारा चली गयी दूरी अधिक है अत: बंदर को एक बिन्दु वस्तु माना जा सकता है।

प्रश्न 5.
कोई खिलाड़ी एक गेंद को ऊपर की ओर आरंभिक चाल 29 मी/सेकण्ड से फेंकता है
(a) गेंद की ऊपर की ओर गति के दौरान त्वरण की दिशा क्या होगी?
(b) इसकी गति के उच्चतम बिन्दु पर गेंद के वेग व त्वरण क्या होंगे?
(c) गेंद के उच्चतम बिन्दु पर स्थान व समय को x = 0 व t= 0 चुनिये, ऊर्ध्वाधर नीचे की ओर की दिशा को X-अक्ष की धनात्मक दिशा मानिए। गेंद की ऊपर की व नीचे की ओर गति के दौरान स्थिति, वेग व त्वरण के चिन्ह बताइए।
उत्तर-
(a) गेंद गुरुत्व के आधीन गति कर रही है, गुरुत्वीय त्वरण की दिशा ऊर्ध्वाधर नीचे की ओर है।
(b) उच्चतम बिन्दु पर गेंद का वेग शून्य एवं त्वरण का मान 9.8 m/s² ऊर्ध्वाधर नीचे की ओर है।
(c)

• ऊपर की गति के लिए-स्थिति एवं वेग ऋणात्मक तथा त्वरण धनात्मक होगा।
• नीचे की ओर गति के लिए-स्थिति, वेग एवं त्वरण तीनों धनात्मक होंगे।

प्रश्न 6.
गति के प्रथम समीकरण का निगमन ग्राफीय विधि से कीजिए।
उत्तर-
गति का प्रथम समीकरण v = u + at ; एकसमान त्वरित गति के लिए (v – t) ग्राफ नीचे प्रदर्शित हैं

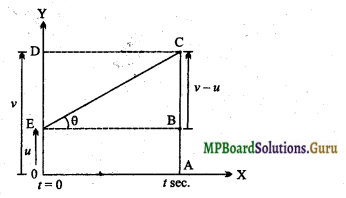
उपरोक्त ग्राफ से स्पष्ट है कि कण का प्रारंभिक वेग t= 0 पर u है तथा t सेकण्ड पश्चात् वेग v हो जाता है। ग्राफ की प्रकृति एक सरल रेखा है।
त्रिभुज EBC में, tanθ = \(\frac{\mathrm{BC}}{\mathrm{EB}}\)
या
tanθ =\(\frac{v-u}{t-0}\)
∵ सरल रेखा का ढाल = त्वरण
अतः a= \(\frac{v-u}{t}\)
या
v-u = at
⇒ v =u+at.

प्रश्न 7.
आपेक्षिक वेग से आप क्या समझते हैं ? इसके लिए व्यंजक ज्ञात कीजिए।
उत्तर-
किसी गतिशील या स्थिर वस्तु के सापेक्ष दूसरी वस्तु का आपेक्षिक वेग वह दर है जिससे कि पहली वस्तु के सापेक्ष दूसरी वस्तु की स्थिति बदलती है।
मानलो A और B दो वस्तुएँ एकविमीय गति कर रही हैं। उनके वेग क्रमशः v₁ और v₂, हैं। यदि समय t पर उनके स्थिति निर्देशांक x₁(t) व x₂(t) हों, तो
x₁(t) = x₁ (0)+v₁t ……………………… (1)
तथा x₂(t) = x₂ (0)+v₂t ……………………… (2)
जहाँ, x₁(0) और x₂ (0) समय t= 0 पर उनके स्थिति निर्देशांक हैं।
समी. (2) से समी. (1) को घटाने पर,
x₂(t) – x₁(t) = x₂ (0) – x₁ (0)+ (v₂ – v₁)t …………. (3)
समी. (3) में x₂(t) -x₁(t) समय t पर वस्तु A के सापेक्ष वस्तु B की आपेक्षिक स्थिति को प्रदर्शित करता है। x₂(0) – x₁(0) समय t=0 पर वस्तु A के सापेक्ष वस्तु B की आपेक्षिक स्थिति या आपेक्षिक दूरी को प्रदर्शित करता है।
समी. (3) में यदि t= 1 सेकण्ड रखें तो v₂ – v₁ एक सेकण्ड में उनका आपेक्षिक विस्थापन होगा।

अतः v₂ – v₁वस्तु A के सापेक्ष वस्तु B का आपेक्षिक वेग होगा।
अब समी. (3) से A के सापेक्ष B का आपेक्षिक वेग,
v₂ – v₁ = \(\frac{\left[x_{2}(t)-x_{1}(t)\right]-\left[x_{2}(0)-x_{1}(0)\right]}{t}\)
यही अभीष्ट व्यंजक है।

प्रश्न 8.
ग्राफीय विधि के द्वारा गति के द्वितीय समीकरण का निगमन कीजिए।
उत्तर-
एकसमान त्वरित गति में वेग-समय ग्राफ एवं समय अक्ष के बीच घिरा क्षेत्रफल वस्तु के विस्थापन के बराबर होता है।
वस्तु का विस्थापन = क्षेत्र OACE का क्षेत्रफल
= आयत OABE का क्षेत्रफल + Δ EBC का क्षेत्रफल
s=OA × AB+\(\frac{1}{2} \) EB × BC.
s=ut+\(\frac{1}{2} \)t(v – u)
∵ v – u = at

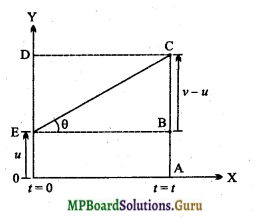
अतः s = ut +\(\frac{1}{2} \)t × at
∴ s = ut + \(\frac{1}{2} \)at².

प्रश्न 9.
ग्राफीय विधि से गति के तृतीय समीकरण का निगमन कीजिए।
उत्तर-
उपरोक्त (v-t) ग्राफ के अनुसार, वस्तु का विस्थापन s = समलम्ब चतुर्भुज OACE का क्षेत्रफल
s = \(\frac{1}{2} \) (AC+OE) EB
या s = \(\frac{1}{2} \)(v -u)t
∵ t = \(\frac{v-u}{a}\)
या v – u = at

अतः s = \(\frac{1}{2} \) (v+u) \(\frac{(v-u)}{a}\)
या s = \(\frac{v^{2}-u^{2}}{2 a} \)
या 2as = v² – u²
⇒ v² = u² + 2as.

 

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
समाकलन विधि से गति के द्वितीय एवं तृतीय समीकरणों का निगमन कीजिए।
उत्तर-
वेग के परिभाषा अनुसार,
v=\(\frac{d x}{d t}\) = विस्थापन परिवर्तन की दर
dx = vdt ⇒ dx = (u + at) dt
या dx = udt + at. dt

दोनों पक्षों का समाकलन करने पर,
\(\int_{0}^{x}\) dx= u \(\int_{0}^{t}\)dt+ a\(\int_{0}^{t}\).dt
या [x]^x₀ = u [t]^t₀ +a \(\left[\frac{t^{2}}{2}\right]_{0}^{t} \)
या [x -0] = u [t -0]+a\(\left[\frac{t^{2}}{2}-0\right]\)
या s = ut + \(\frac{1}{2}\)at² (द्वितीय समीकरण)

त्वरण के परिभाषा अनुसार,
a = \(\frac{d v}{d t}\) = \(\frac{d v}{dx}\) × \(\frac{dx}{dt}\) = v . \(\frac{dv}{dx}\) (∵ v = \(\frac{dv}{dx}\) )
या adx = vdv
उपरोक्त समीकरण के दोनों पक्षों का समाकलन करने पर,
a\(\int_{0}^{x}[latex] .dx= [latex]\int_{u}^{v}[latex] vdv
या a[x]₀^x = [latex]\left[\frac{v^{2}}{2}\right]_{u}^{v}\)
या a [x -0] = \(\left[\frac{v^{2}}{2}-\frac{u^{2}}{2}\right] \)
या as = \(\frac{v^{2}-u^{2}}{2}\)
⇒ v² – u² = 2as (गति का तृतीय समीकरण)।

प्रश्न 2.
ग्राफीय विधि से गति के द्वितीय एवं तृतीय समीकरण का निगमन कीजिए।
उत्तर-
उत्तर के लिए लघु उत्तरीय प्रश्न क्रमांक 8 एवं 9 देखिए।

आंकिक प्रश्न

प्रश्न 1.
एक कार एक शहर A से दूसरे शहर B तक 40 किमी/घंटा की चाल से जाती है तथा 60 किमी/घण्टा की चाल से वापस आती है। कार की औसत चाल तथा औसत वेग ज्ञात कीजिए।
हल-माना दोनों शहरों के बीच की दूरी x किमी है।
अतः

अतः कार को A से B तक जाने में लगा समय t₁ = \(\frac{x}{40}\) घण्टे
एवं कार को B से A तक वापस आने में लगा समय t₂ = \(\frac{x}{60}\) घण्टे
∴

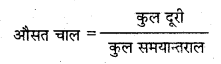
= \(\frac{x+x}{\frac{x}{40}+\frac{x}{60}}\) = \(\frac{2}{\frac{1}{40}+\frac{1}{60}}\) = \(=\frac{2 \times 2400}{60+40}\)
= \(\frac{2 \times 2400}{100}\) = 48 किमी/घण्टा।

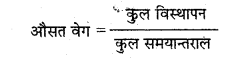
= \(\frac{0}{\frac{x}{40}+\frac{x}{60}}\) = 0

प्रश्न 2.
विराम से चलकर कोई पिण्ड 3 सेकण्ड में 10 मीटर प्रति सेकण्ड का वेग प्राप्त कर लेता है। त्वरण क्या होगा?
हल-
दिया गया है-प्रारंभिक वेग u = 0 (विरामावस्था), t = 3 सेकण्ड, अंतिम वेग v = 10 मीटर/सेकण्ड
अतः सूत्र v = u + at में मान रखने पर,
10 = 0+a × 3
a = \(\frac{10}{3}\) मीटर/सेकण्ड² = 3.33 मीटर/सेकण्ड²।

प्रश्न 3.
एक पिण्ड विराम से चलकर आठवें सेकण्ड में एकसमान त्वरण से चलकर 45 मीटर की दूरी चलता है तो पिण्ड का त्वरण ज्ञात कीजिये।
हल- दिया है-
u= 0, t = 8,s = 45 मीटर।
अत: सूत्र s = u+\(\frac{1}{2}\) a(2t-1) में मान रखने पर,
45 = 0 +\(\frac{1}{2}\) a(2 × 8-1)
= \(\frac{1}{2}\) a(15)
अतः a = \(\frac{45 \times 2}{15}\) = 6 मीटर/सेकण्ड²।

प्रश्न 4.
एक कार 30 किमी/घण्टा के वेग से चल रही है। ब्रेक लगाने पर वह 10 मीटर चलकर रुक जाती है, कार को रुकने में लगा समय ज्ञात कीजिए।
हल- कार का प्रारंभिक वेग u = 30 किमी/घण्टा
= \(\frac{30 \times 1000}{60 \times 60}\) मीटर/सेकण्ड।
u =\(=\frac{25}{3} \) मीटर/सेकण्ड
s = 10 मीटर, अंतिम वेग v= 0

अतः v² =u +2as में मान रखने पर,
0 = \(\left(\frac{25}{3}\right)^{2}\) +2a (10)
अतः –\(\frac{625}{9}\) = 20a
अतः a = \(=\frac{-625}{9 \times 20}\) = \(\frac{-125}{36}\) मीटर/सेकण्ड²
पुनः v = u +at से
0 = \(\frac{25}{3} \) – \(\frac{125}{36} \) × t
अतः t = \(\frac{25}{3} \) ×\(\frac{36}{125} \) = \(\frac{12}{5} \) = 2.4 सेकण्ड

प्रश्न 5.
एक पिण्ड 6 वें सेकण्ड में 15 मीटर तथा 10 वें सेकण्ड में 23 मीटर की दूरी तय करता है। पिण्ड का प्रारंभिक वेग तथा त्वरण ज्ञात कीजिए।
हल-सूत्र s = u+\(\frac{1}{2}\) a(2t-1) में मान रखने पर,
15=u+ \(\frac{1}{2}\)a( 2 × 6-1) = u+\(\frac{a}{2}\) (11)
∴ 2u+11a = 30 …………….. (1)
एंव 23 = u+\(\frac{1}{2}\) (2 × 10-1) = u+\(\frac{a}{2}\) (19)
∴ 2u+19a = 46 ………………… (2)
समी. (1) तथा (2) को हल करने पर, u = 4 मीटर/सेकण्ड, a = 2 मीटर/सेकण्ड² ।

प्रश्न 6.
दो रेलगाड़ियाँ समान्तर पटरियों पर एक ही दिशा में क्रमशः 10 मीटर/सेकण्ड तथा 15 मीटर/सेकण्ड के वेग से चल रही हैं। पहली रेलगाड़ी के सापेक्ष दूसरी रेलगाड़ी का वेग ज्ञात कीजिए।
हल-दिया है- v₁ = 10 मीटर/सेकण्ड, v₂ = 15 मीटर/सेकण्ड अतः पहली रेलगाड़ी के सापेक्ष दूसरी रेलगाड़ी का आपेक्षिक वेग
आपेक्षिक वेग = v₂ – v₁
=15-10 = 5 मीटर/सेकण्ड।

प्रश्न 7.
सीधे राजमार्ग पर कोई कार 126 किमी/घण्टा की चाल से चल रही है। इसे 200 मीटर की दूरी पर रोक दिया जाता है। कार के मंदन को एकसमान मानिए और इसका मान ज्ञात कीजिए। कार को रुकने में कितना समय लगा?
हल-कार का प्रारंभिक वेग u = 126 किमी/घण्टा = 126 × \(/frac{5}{18} \) मीटर/सेकण्ड
= 35 मीटर/सेकण्ड
कार का अंतिम वेग v= 0, s = 200 मीटर
गति के तृतीय समीकरण से,
v² = u² +2as
या a = \(\frac{v^{2}-u^{2}}{2 s}\) = \(\frac{(0)^{2}-(35)^{2}}{2 \times 200}\) = -3.06 मीटर/सेकण्ड²
मंदन = 3.06 मीटर/सेकण्ड²
कार के द्वारा लिया गया समय t = \(\frac{v-u}{q}\)
=\(\frac{0-35}{-3 \cdot 06}\) =11.44 सेकण्ड।

प्रश्न 8.
एक कार कुल दूरी का \(\frac{1}{3}\) भाग 10 किमी/घण्टा,\(\frac{1}{3}\) भाग 20 किमी/घण्टा तथा शेष ,\(\frac{1}{3}\) भाग 60 किमी/घण्टा की चाल से तय करती है। कार की औसत चाल ज्ञात कीजिए।
हल-माना कार द्वारा चली गई कुल दूरी = x किमी v₁ = 10 किमी/घण्टा, v₂ = 20 किमी/घण्टा, v₃ = 60 किमी/घण्टा
∴ कार की औसत चाल v= \(\frac{x}{t_{1}+t_{2}+t_{3}}\)
∴ v = \(\frac{x}{\frac{x}{3 v_{1}}+\frac{x}{3 v_{2}}+\frac{x}{3 v_{3}}}\) = \(\frac{x}{\frac{x}{3}\left(\frac{1}{v_{1}}+\frac{1}{v_{2}}+\frac{1}{v_{3}}\right)}\)
या v = \(\frac{3}{\frac{1}{10}+\frac{1}{20}+\frac{1}{60}}\) = \(\frac{3 \times 60}{6+3+1}\)
∴ v = \(\frac{180}{10}\) = 18 किमी/घण्टा।

प्रश्न 9.
एक गेंद जो ऊर्ध्वाधर ऊपर की ओर फेंकी गई है, 100 मीटर ऊँचे मकान की छत तक पहुँचती है। उसी क्षण दूसरी गेंद मकान की छत से ऊर्ध्वाधर नीचे की ओरशून्य प्रारंभिक वेग से गिराई जाती है। किस ऊँचाई पर ये गेंदें एक-दूसरे के पास से गुजरेंगी?
हल
h= 100 मीटर माना पृथ्वी से x मीटर की ऊँचाई पर दोनों गेंदें t समय के बाद एक-दूसरे के पास से गुजरती हैं।
ऊर्ध्वाधर ऊपर की ओर गति के लिए, u = ?, v = 0, a =-g तथा h = 100 मीटर।
सूत्र v² = u² +2as से,
0 = u – 2g × 100
या u² = 200g = 200 × 9.8 = 1960
∴ u = \(14 \sqrt{10}\) मीटर/सेकण्ड
ऊर्ध्वाधर नीचे की गति के लिए – u = 0, a =g, s = (100-x)

अत: सूत्र- s= ut + \(\frac{1}{2}\) at² से,
100 – x = 0+\(\frac{1}{2}\) × 9.8 × 12 = 4.9t² …………………… (1)
नीचे से ऊपर फेंकी जाने वाली गेंद के लिए दूरी
s = ut + \(\frac{1}{2}\) at²
∴ x = \(14 \sqrt{10} t-\frac{1}{2} g t^{2} \) = \(14 \sqrt{10} t\) – 4.9t² ………………. (2)
समी. (1) तथा (2) को जोड़ने पर,
100 – x + x = \(14 \sqrt{10} t\) -4.9t²+4.9t²
या \(14 \sqrt{10} t\) = 100
∴ t = \(\frac{100}{14 \sqrt{10}}\) = \(\frac{10 \sqrt{10}}{14}\) सेकण्ड

समी. (1) में t का मान रखने सर,
100-x= 4.9x \(\left(\frac{10 \sqrt{10}}{14}\right)^{2} \) = 4.9 x \(\frac{1000}{196}\) = 25
∴ x = 100-25 = 75 मीटर
अतः पृथ्वी से 75 मीटर ऊँचाई पर दोनों गेंदें एक-दूसरे के पास से गुजरेंगी।

प्रश्न 10.
एक मीनार की चोटी से चार गेंदें एक-एक सेकण्ड के अन्तर से स्वतन्त्रतापूर्वक गिरायी जाती हैं। पहली गेंद छोड़ने के 4 सेकण्ड के बाद पृथ्वी पर पहुँचती हैं। उस क्षण पहली व दूसरी, दूसरी व तीसरी, तीसरी व चौथी गेंद के बीच दूरी ज्ञात कीजिए। (g = 9.8 मीटर/सेकण्ड²
हल-गेंद को ऊपर से स्वतन्त्रतापूर्वक गिराने में चली गई दूरी
s = ut+\(\frac{1}{2}\) at² से, .
s = 0+ \(\frac{1}{2}\) gt² = \(\frac{1}{2}\) gt²
पहली गेंद द्वारा 4 सेकण्ड में चली गई दूरी
s₄ = \(\frac{1}{2}\) gt² × 9.8 × 16 = 4.9 × 16 मीटर
दूसरी गेंद द्वारा 3 सेकण्ड में चली गई दूरी
s₃ = 4.9t² = 4.9 × 9 ।

अत: पहली तथा दूसरी गेंद के बीच की दूरी
s₄ – s₃ = 4.9 × (16-9)= 4.9 × 7 = 34.3 मीटर।
इसी प्रकार, दूसरी व तीसरी गेंदों के बीच की दूरी
s₃ – s₂ = \(\frac{1}{2} g\left(t_{3}^{2}-t_{2}^{2}\right) \) = \(\frac{1}{2}\) × 9.8 × (9-4)
s₃ – s₂ = 4.9 × 5 = 24.5 मीटर।
तीसरी व चौथी गेंदों के बीच की दूरी
s₂ – s₁ =\(\frac{1}{2}\)g(t²₂ – t²₁) = \(\frac{1}{2}\) × 9.8 × (4-1) = 4.9 × 3 = 14.7 मीटर। उत्तर

प्रश्न 11.
एक हेलीकॉप्टर जो 2 मीटर/सेकण्ड के एकसमान वेग से ऊपर जा रही है, से खाने का पैकेट गिराया जाता है। 2 सेकण्ड बाद
(i) पैकेट का वेग क्या होगा ?
(ii) पैकेट हेलीकॉप्टर से कितना नीचे है ? (g = 9.8 मीटर/सेकण्ड²)
हल- (i) u = -2 मीटर/सेकण्ड, g = 9.8 मीटर/सेकण्ड², v = ?, t = 2 सेकण्ड
सूत्र v=u+at से,
v=-2+9.8 × 2 = 17.6 मीटर/सेकण्ड
अतः पैकेट का नीचे की ओर वेग 17.6 मीटर/सेकण्ड होगा।
(ii) माना 2 सेकण्ड बाद पैकेट हेलीकॉप्टर से h मीटर नीचे है।
सूत्र- s = ut+\(\frac{1}{2}\)gt² से,
h= 0+\(\frac{1}{2}\) ×9.8 × 2 = 19.6 मीटर।

प्रश्न 12.
एक जेट हवाई जहाज 500 किमी/घण्टा की चाल से गतिमान है और इसमें से गैसें जहाज के सापेक्ष 1500 किमी/घण्टा की चाल से निकलती है। गैसों की जमीन पर खड़े दर्शक के सापेक्ष चाल ज्ञात कीजिए।
हल-गैसों की जमीन पर खड़े दर्शक के सापेक्ष चाल
=vg-v_j = 1500-500 = 1000 किमी/घण्टा।

प्रश्न 13.
54 किमी/घण्टा की चाल से गतिमान ट्रेन की खिड़की के पास बैठा यात्री 36 किमी/घण्टाकी चाल से विपरीत दिशा में गतिमान ट्रेन को देखता है। यदि दूसरी ट्रेन की लंबाई 150 मीटर हो तो यात्री के सामने से यह ट्रेन कितने समय में गुजरेगी?
हल- ट्रेन A का वेग v_A = 54 किमी/घण्टा
ट्रेन B का वेग v_B = -36 किमी/घण्टा
अतः ट्रेन A का ट्रेन B के सापेक्ष वेग
v_R = v_A – v_B = 54-(-36)
= 54+36 = 90 किमी/घण्टा
v_R = \(=\frac{90 \times 1000}{60 \times 60}\) = 25 मीटर/सेकण्ड.

चूँकि ट्रेन B की लंबाई l = 150 मीटर
ट्रेन B को यात्री के सामने से गुजरने में लगा समय
t = \(\frac{l}{v_{\mathrm{R}}}\) = \(\frac{150}{25}\) =6 सकण्ड .

प्रश्न 14.
संलग्न चित्र में किसी कार यात्रा का समयविस्थापन ग्राफ दिया है, अतः ज्ञात कीजिए
(i)5 वें तथा 11वें मिनट में विस्थापन,
(ii) 11 मिनट में कार द्वारा चली दूरी,
(iii) कार कब से कब तक ठहरी रहती है ?
(iv) कार का पहले चार मिनटों में औसत वेग तथा पहले मिनटों में औसत वेग,
(v) कार सबसे धीमी कब चलती है ?
(vi) 14 वें मिनट पर कार कहाँ है?

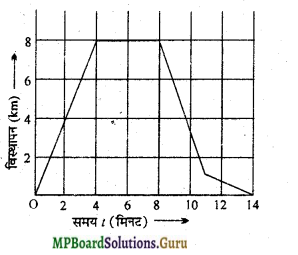
हल –
(i) 5वें मिनट पर कार का विस्थापन = 8 किमी 11वें मिनट में कार का विस्थापन = 2 किमी।
(ii) 11 मिनट में कार द्वारा चली गई दूरी = d₁+ d₂ + d₃
=8+0+ (8-2)= 8+6 = 14 किमी।
(iii) कार चौथे से आठवें मिनट तक ठहरी रहती है तथा फिर लौटने लगती है।
(iv) पहले 4 मिनट में कार का औसत वेग

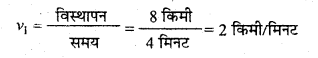
मिनट अगले चार मिनटों में कार का औसतं वेग
v₂ = 0
पहले 8 मिनट में कार का औसत वेग
v_a = \(\frac{v_{1}+v_{2}}{2}\) = \(\frac{2+0}{2}\) = 1किमी/ मिनट
(v) कार 11 से 14 मिनट के बीच सबसे धीमी चलती है।
(vi) कार चौदहवें मिनट में अपने प्रारंभिक स्थान पर पहुँच जाती है।

प्रश्न 15.
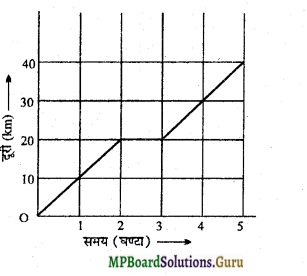
संलग्न चित्र में एक साइकिल सवार का दूरी-समय ग्राफ दिखाया गया है।ज्ञात कीजिए
(i) साइकिल सवार की अधिकतम चाल,
(ii) संपूर्ण यात्रा में औसत चाल। हल-साइकिल सवार की चाल 2 घंटे में शून्य से बढ़कर v हो जाती है। अतः

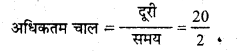
= 10 किमी/घण्टा।

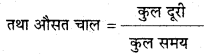
v_a = \(\frac{d_{1}+d_{2}+d_{3}}{5}\)
= \(\frac{20+0+15}{5}\) = \(\frac{35}{5}\) = 7 किमी/घण्टा।

प्रश्न 16.
एक महिला अपने घर से प्रातः 9:00 बजे 2-5 किमी दूर अपने कार्यालय के लिए सीधी सड़क पर 5 किमी/घण्टा की चाल से चलती है। वहाँ वह सायं 5.00 बजे तक रहती है और 25 किमी/ घण्टा की चाल से चल रही किसी आटो रिक्शा द्वारा अपने घर लौट आती है। उपर्युक्त पैमाना चुनिये तथा उसकी गति का (x-t) ग्राफ खींचिए।
हल-महिला द्वारा घर से कार्यालय तक जाने में लिया गया समय

 

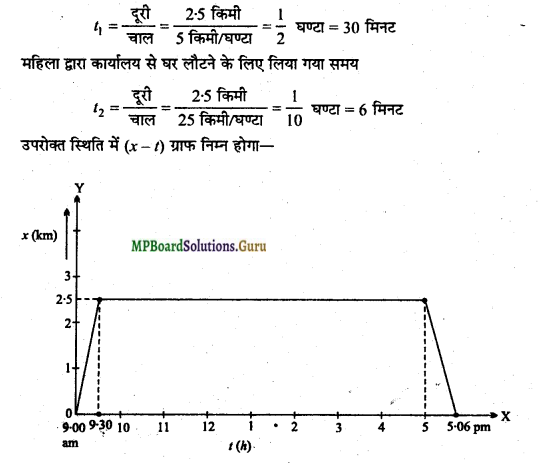
1. वस्तुनिष्ठ प्रश्न

प्रश्न 1.
किसी गतिशील पिण्ड का वेग दुगुना कर देने पर दुगुना हो जाता है
(a) त्वरण
(b) गतिज ऊर्जा
(c) संवेग
(d) भार ।
उत्तर:
(c) संवेग

प्रश्न 2.
एक मीनार के शिखर से छोड़ा गया पिण्ड 2 सेकण्ड में आधी ऊँचाई पार कर लेता है, तो उस मीनार की ऊँचाई क्या होगी यदि g = 9.8 मीटर/सेकण्ड² हो-
(a) 9.8 मी.
(b) 19.6 मी.
(c) 20 मी.
(d) 39.2 मी.।
उत्तर:
(d) 39.2 मी.।

प्रश्न 3.
तात्क्षणिक वेग और तात्क्षणिक चाल का अनुपात होता है
(a) 1 से कम
(b) 1 से ज्यादा
(c) 0
(d) 1 के बराबर।
उत्तर:
(d) 1 के बराबर।

प्रश्न 4.
किसी त्वरण व समय के बीच खींचे गए ग्राफ का क्षेत्रफल दर्शाता है
(a) विस्थापन
(b) वेग
(c) वेग में परिवर्तन
(d) तय की गई दूरी।
उत्तर:
(c) वेग में परिवर्तन

प्रश्न 5.
एक वस्तु गुरुत्वीय क्षेत्र में स्वतन्त्रतापूर्वक गिरना प्रारम्भ करती है। उसके द्वारा प्रथम, द्वितीय व तृतीय सेकण्ड में तय की गई दूरियों का अनुपात होगा
(a) 1: 3:5
(b) 1 : 2 : 3
(c) 1 : 4 :9
(d) 1: 5: 6.
उत्तर:
(a) 1: 3:5

प्रश्न 6.
गैस के अणुओं की गति होती है
(a) एकविमीय
(b) द्विविमीय
(c) त्रिविमीय
(d) केवल ऊपर नीचे।
उत्तर:
(c) त्रिविमीय

प्रश्न 7.
किसी गतिमान कण के लिये शून्य हो सकता है
(a) विस्थापन
(b) दूरी
(c) चाल
(d) इनमें से कोई नहीं।
उत्तर:
(a) विस्थापन

प्रश्न 8.
कोई खिलाड़ी एक गेंद को ऊपर की ओर आरंभिक चाल 29 m/s से फेंकता है तो इसके गति के उच्चतम बिन्दु पर वेग का मान होगा
(a) 29 m/s
(b)-29 m/s
(c) शून्य
(d) इनमें से कोई नहीं।
उत्तर:
(c) शून्य

प्रश्न 9.
एक कार दो स्थानों के मध्य की आधी दूरी 40 km/hr की चाल से तथा अगली आधी दूरी 60 km/hr की चाल से तय करती है, कार की औसत चाल होगी
(a) 40 km/hr
(b) 48 km/hr
(c) 50 km/hr
(d) 60 km/hr.
उत्तर:
(b) 48 km/hr

प्रश्न 10.
किसी कण की स्थिति सदिश समीकरण x = (3t³+ 7t² +14t+8)m से दी गयी है, कण का त्वरण t=1 sec. पर होगी
(a) 10 m/s²
(b) 32 m/s²
(c) 23 m/s²
(d) 16 m/s²
उत्तर:
(b) 32 m/s²

2. सही जोड़ियाँ बनाइए

खण्ड ‘अ’	खण्ड ‘ब’
1. गति का प्रथम समीकरण	(a) u+\(\frac{1}{2}\)a(2t-1)
2. गति का द्वितीय समीकरण	(b) चाल
3. मन्दन का मात्रक	(c) v2 =u2 + 2as
4. एकांक समय में चली गई दूरी	(d) मीटर/सेकण्ड
5. 1 वें सेकण्ड में चली गई दूरी	(e) s = ut+ \(\frac{1}{2}\)at2
	(f) v = u +at

उत्तर:
1. (f) v = u +at
2. (e) s = ut+ \(\frac{1}{2}\)at²
3. (d) मीटर/सेकण्ड²
4. (b) चाल
5. (a) u+\(\frac{1}{2}\)a(2t-1).

3. सत्य/असत्य बताइए

1. वेग-समय ग्राफ से वस्तु द्वारा चली गई दूरी ज्ञात कर सकते हैं।
उत्तर:
सत्य

2. विस्थापन शून्य, ऋणात्मक या धनात्मक हो सकता है।
उत्तर:
सत्य

3. एकसमान गति के लिए त्वरण शून्य होता है।
उत्तर:
सत्य

4. यह सम्भव है कि दूरी शून्य हो किन्तु विस्थापन शून्य न हो।
उत्तर:
सत्य

5. विस्थापन तभी शून्य होगा.जबकि दूरी शून्य हो।
उत्तर:
असत्य।

4. रिक्त स्थानों की पूर्ति कीजिये

1. वेग परिवर्तन की दर को ……………. कहते हैं।
उत्तर:
त्वरण

2. किसी गतिमान वस्तु की स्थिति परिवर्तन की दर को उस वस्तु की …………… कहते हैं।
उत्तर:
चाल

3. तात्क्षणिक चाल ज्ञात करने वाले यंत्र का नाम ……………….. है।
उत्तर:
चालमापी (Speedometer)

4. परिवर्ती गति में किसी क्षण पर वस्तु के वेग को उसका ……………. कहते हैं।
उत्तर:
तात्क्षणिक वेग

5. किसी निश्चित दिशा में वस्तु द्वारा तय की गई दूरी को उसका ……………. कहते हैं।
उत्तर:
विस्थापन

6. विलियर्ड बाल की गति …………… गति होती है।
उत्तर:
द्विविमीय।