MP Board Class 11th Maths Solutions Chapter 11 शंकु परिच्छेद Ex 11.2
निम्नलिखित प्रश्न 1 से 6 तक प्रत्येक में नाभि के निर्देशांक, परवलय का अक्ष, नियता का समीकरण और नाभिलंब जीवा की लंबाई ज्ञात कीजिए।
प्रश्न 1.
y2 = 12x.
हल:
परवलय का समीकरण, y2 = 12x
∴ y2 = 4ax से तुलना करने पर
4a= 12 या a= 3
(i) नाभि के निर्देशांक (a, 0) या (3, 0)
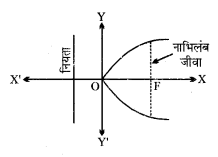
(ii) परवलय का अक्ष OX
इसका समीकरण y = 0
(iii) नियता का समीकरण : x = – a अर्थात् x = – 3
(iv) नाभिलंब जीवा की लंबाई = 4a = 12.
![]()
प्रश्न 2.
x2 = 6y.
हल:
परवलय का समीकरण x2 = 6y
∴ 4a = 6 या a = \(\frac{3}{2}\)
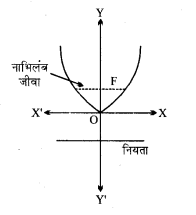
इसका अक्ष y-अक्ष है जिसका
(i) समीकरण x = 0 है।
(ii) नाभि F (0, a) के निर्देशांक \(\left(0, \frac{3}{2}\right)\) है।
(iii) नियता y = – a का समीकरण y = – \(\frac{3}{2}\)
(iv) नाभिलंब जीवा की लम्बाई 4a = 6.
प्रश्न 3.
y2 = – 8x.
हल:
परवलय का समीकरण y2 = – 8x
∴ 4a = 8, a = 2
(i) नाभि F(- a, 0) के निर्देशांक (- 2, 0)
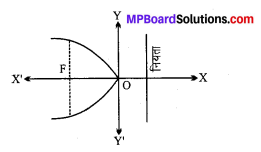
(ii) परवलय का अक्ष x-अक्ष
इसका समीकरण y = 0
(iii) नियता x = a का समीकरण x = 2.
(iv) नाभिलंब जीवा की लंबाई = 4a = 8.
प्रश्न 4.
x2 = – 16y.
हल:
परवलय का समीकरण x2 = – 16y
∴ 4a = 16 या a = 4
नियता
(i) नाभि F (0, – a) के निर्देशांक (0, – 4)
(ii) परवलय अक्ष का समीकरण x = 0.
(iii) नियता y = 0 का समीकरण y = 4.
(iv) नाभिलंब जीवा की लंबाई 4a = 16.
![]()
प्रश्न 5.
y2 = 10x.
हल:
परवलय का समीकरण y2 = 10x (आकृति प्रश्न 1 में देखें)
4a = 10 या a = \(\frac{5}{2}\)
(i) नाभि F (a, 0) के निर्देशांक \(\left(\frac{5}{2}, 0\right)\)
(ii) परवलय का अक्ष : x-अक्ष, समीकरण y = 0
(iii) नियता x = – a का समीकरण x = – \(\left(\frac{5}{2}, 0\right)\)
(iv) नाभिलंब जीवा की लंबाई 4a = 10.
प्रश्न 6.
x2 = – 9y.
हल:
परवलय का समीकरण x2 = – 9y (आकृति प्रश्न 4 में देखें)
4a = 9 या a = \(\frac{9}{4}\)
(i) नाभि (0, – a) के निर्देशांक \(\left(0,-\frac{9}{4}\right)\)
(ii) परवलय का अक्ष : y-अक्ष, समीकरण x = 0
(iii) नियता y = a का समीकरण y = \(\frac{9}{4}\)
(iv) नाभिलंब जीवा की लंबाई 4a = 9.
निम्नलिखित प्रश्न 7 से 12 तक प्रत्येक में परवलय का समीकरण ज्ञात कीजिए जो दिए प्रतिबंध को संतुष्ट करता है।
प्रश्न 7.
नाभि (6, 0), नियता x = – 6.
हल:
परवलय का अक्ष : x-अक्ष, y = 0
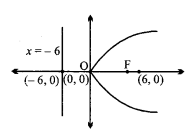
शीर्ष (0, 0) है, नाभि के निर्देशांक (6, 0)
परवलय का अक्ष, धन x-अक्ष के अनुदिश है।
परवलय का समीकरण y2 = 24x.
प्रश्न 8.
नाभि (0, – 3), नियता y = 3.
हल:
परवलय का अक्ष y-अक्ष है।
शीर्ष (0, – 3), (0, 3) का मध्य बिन्दु (0, 0) है। नाभि (0, – 3) से स्पष्ट होता है कि परवलय की अक्ष OY के अनुदिश है।
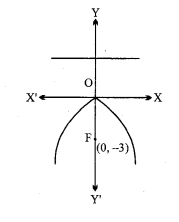
∴ परवलय के समीकरण का रूप x2 = – 4ay
यहाँ पर a = 3, ∴ 4a = 12
∴ परवलय का समीकरण x2 = – 12y.
![]()
प्रश्न 9.
शीर्ष (0, 0), नाभि (3, 0) (आकृति प्रश्न 7 की देखिए)
हल:
परवलय का अक्ष OX के अनुदिश हैं।
∴ परवलय के समीकरण का रूप y2 = 4ax
नाभि (3, 0) है। ∴ a = 3
4a = 4 x 3 = 12
∴ परवलय का समीकरण y2 = 12x.
प्रश्न 10.
शीर्ष (0, 0), नाभि (-2, 0).
हल:
परवलय का अक्ष OX’ के अनुदिश
नाभि (- 2, 0) है तो a= 2
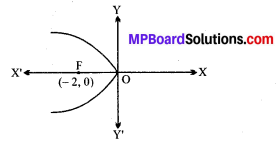
∴ 4a = 8
परवलय का रूप y2 = – 4ax
परवलय का समीकरण y2 = – 8x.
प्रश्न 11.
शीर्ष (0, 0), (2, 3) से जाता है और अक्ष, x-अक्ष के अनुदिश है।
हल:
परवलय का शीर्ष (0, 0) है और अक्ष : x-अक्ष है।
∴ परवलय के समीकरण का रूप y2 = 4ax
यह बिन्दु (2, 3) से होकर जाता है
∴ 9 = 4a.2 या 4a = \(\frac{9}{2}\)
अतः परवलय का समीकरण y2 = \(\frac{9}{2}\)x या 2y2 = 9x.
![]()
प्रश्न 12.
शीर्ष (0, 0), (5, 2) से जाता है और y-अक्ष के सापेक्ष सममित है।
हल:
शीर्ष (0, 0), परवलय y-अक्ष के सापेक्ष सममित है।
समीकरण का रूप x2 = 4ay है। यह बिन्दु (5, 2) से गुजरता है।
∴ 25 = 4a × 2
∴ 4a = \(\frac{25}{2}\)
∴ परवलय का समीकरण, x2 = \(\frac{25}{2}\)y या 2x2 = 25y