MP Board Class 11th Maths Important Questions Chapter 11 Conic Sections
Conic Sections Important Questions
Conic Sections Objective Type Questions
(A) Choose the correct option :
Question 1.
Coordinates of the focus of the parabola y = 2x2 + x are:
(a) (0, 0)
(b) (\(\frac { 1 }{ 2 }\), \(\frac { 1 }{ 4 }\))
(c) (- \(\frac { 1 }{ 4 }\), 0)
(d) ( – \(\frac { 1 }{ 4 }\), \(\frac { 1 }{ 8 }\))
Answer:
(c) (- \(\frac { 1 }{ 4 }\), 0)
Question 2.
In a ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 a > b, the relation between a, b an eccentricity e is:
(a) b2 = a2(1 – e2)
(b) b2 = a2(e2 – 1)
(c) a2 = b2(1 – e2)
(d) a2 = b2(e2 – 1)
Answer:
(a) b2 = a2(1 – e2)
Question 3.
The length of latus rectum of ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1, represent a circle then its eccentricity will be:
(a) \(\frac { { 2a }^{ 2 } }{ b }\)
(b) \(\frac { { 2b }^{ 2 } }{ a }\)
(c) \(\frac { { a }^{ 2 } }{ b }\)
(d) \(\frac { { b }^{ 2 } }{ a }\)
Answer:
(b) \(\frac { { 2b }^{ 2 } }{ a }\)
![]()
Question 4.
The eccentricity of the parabola is:
(a) Less than 1
(b) Greater than 1
(c) 0
(d) 1
Answer:
(d) 1
Question 5.
The eccentricity of the ellipse is:
(a) Less than 1
(b) Greater than 1
(c) 0
(d) 1
Answer:
(a) Less than 1
Question 6.
The eccentricity of the hyperbola is:
(a) Less than 1
(b) Greater than 1
(c) 0
(d) 1
Answer:
(b) Greater than 1
Question 7.
In a ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1, represent a circle then its eccentricity will be:
(a) Less than 1
(b) Greater than 1
(c) 0
(d) 1
Answer:
(c) 0
Question 8.
The sum of focal distances from any point on the ellipse is:
(a) Equal to major axis
(b) Equal to minor axis
(c) The distance between two foci
(d) Equal to latus rectum.
Answer:
(a) Equal to major axis
Question 9.
The differecne of the focal distances from any point on the hyperbola is:
(a) Equal to its conjugate axis
(b) Equal to its transverse axis
(c) The distance between two foci
(d) Equal to its latus rectum.
Answer:
(b) Equal to its transverse axis
Question 10.
The value of the eccentricity of ellipse 25x2 + 16y2 = 400 is:
(a) \(\frac { 3 }{ 5 }\)
(b) \(\frac { 1 }{ 3 }\)
(c) \(\frac { 2 }{ 5 }\)
(d) \(\frac { 1 }{ 5}\)
Answer:
(a) \(\frac { 3 }{ 5 }\)
Question 11.
Equation ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 represent a circle if:
(a) a = b, c = 0
(b) f = g, h = 0
(c) a = b, h = 0
(d) f = g, c = 0
Answer:
(a) a = b, c = 0
Question 12.
Area of triangle whose centre (1,2) and which is passes through the point (4,6) will be:
(a) 5π
(b) 10π
(c) 25π
(d) 25π2
Answer:
(c) 25π
![]()
Question 13.
The circle passing through (1, – 2) and touching the X – axis at (3,0), also passes through the point:
(a) (2, – 5)
(b) (5, – 2)
(c) (- 2, 5)
(d) (- 5, 2)
Answer:
(a) (2, – 5)
Question 14.
The length of the diameter of the circle which touches the X – axis at the point (1,0) and passes through the point (2,3) is:
(a) \(\frac { 10 }{ 3 }\)
(b) \(\frac { 3 }{ 5 }\)
(c) \(\frac { 6 }{ 5 }\)
(d) \(\frac { 5 }{ 3 }\)
Answer:
(a) \(\frac { 10 }{ 3 }\)
Question 15.
Eccentricity of the hyperbola 3x2 – y2 = 4 :
(a) 1
(b) 2
(c) – 2
(d) \(\sqrt {2}\)
Answer:
(b) 2
(B) Match the following :

Answer:
- (c)
- (e)
- (b)
- (a)
- (d)
- (i)
- (h)
- (f)
- (j)
- (g)
(C) Fill in the blanks :
- The length of the latus rectum of the parabola y2 = 4ax is ……………
- The centre of the ellipse \(\frac { { (x-1) }^{ 2 } }{ 9 } +\frac { { (y-2) }^{ 2 } }{ 4 }\) = 1 will be ……………
- The vertex of the parabola (y – 2)2 = 4a(x -1) is ……………
- The lines \(\frac { x }{ a }\) – \(\frac { y }{ b }\) = m and \(\frac { x }{ a }\) + \(\frac { y }{ b }\) = \(\frac { 1 }{ m }\) meets always at ……………
- If an ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1, a > b and its eccentricity is e, then the foci will be
- Standard form of equation of parabola is ……………
- Parametric equation of a circle x2 + y2 = 4 is ……………
- A line y = x + a\(\sqrt {2}\) touches the circle x2 + y2 = a2 point ……………
- A line y = mx + c touches the circle x2 + y2 = a2 if c = ……………
- Vertex of the parabola 3y2 + 6y – 4x + 11 = 0 is ……………
- Equation 2x2 + 2y2 – 12x – 16y + 4 = 0 represent a point circle if k = ……………
- Radius of circle 3x2 + 3y2 – 5x – 6y + 4 = 0 is ……………
Answer:
- 4a
- (1, 2)
- (1, 2)
- Hyperbola
- (± ae, 0)
- y2 = 4ax
- x = 2cosθ
- (- \(\frac { a }{ \sqrt { 2 } }\), \(\frac { a }{ \sqrt { 2 } }\) )
- ±a\(\sqrt { 1+{ m }^{ 2 } }\)
- (5, 1)
- 50, 12
- \(\sqrt {61}\)
(D) Write true / false :
- Conic section is a locus of the point whose the ratio between the distance from the fixed point and distance from the fixed line, this ratio is called eccentricity of the conic section.
- The ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 has two directrics, the equation of directrics are x = ± \(\frac { a }{ e }\); Where a > b and y = ± \(\frac { b }{ e }\) ; where b > a.
- The foci of the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 are (0, ± be) where a < b.
- A circle drawn by taking major axis of the ellipse as diameter is called auxiliary circle of the ellipse.
- The locus of intersection point of the lines bx + ay = abt and bx – ay = \(\frac { ab}{ t }\) will be a ellipse.
- The focus of a parabola x2 = – 16y will be (0, – 4).
- Equation x2 + y2 – 6x + 8y + 50 = 0 represent a circle.
- Circle x2 + y2 = 9 and x2 + y2 + 8y + c = 0 touches externally if c = 15 .
- Eccentricity of hyperbola is 1.
- Minimum distance between line y – x = 1 and curve x = y2 is \(\frac { 3\sqrt { 2 } }{ 8 }\)
Answer:
- True
- True
- True
- True
- False
- True
- False
- True
- False
- True
(E) Write answer in one word / sentence :
- If the circle x2 + y2 + 2ax + 8y +16 = 0, touches X – axis, then the value of α will be.
- Coordinate of focus of parabola x2 = – 10y will be.
- Write the equation of a circle whose centre is (2,2) and passes through the point (4, 5).
- The centre of a circle is (5, 7) and touches Y – axis, then its radius will be.
- If the radius of a circle x2 + y2 – 6x + ky – 25 = 0 is \(\sqrt {38}\) the value of k will be.
- Vertex of the parabola y = x2 – 2x + 3 will be.
- Equation of a parabola whose vertex (0, 0) and focus (0, 3) will be.
- Length of major axis of ellipse 9x2 + 16y2 = 144 will be.
- Eccentricity of an ellipse whose latus rectum in half of its minor axis will be.
- Equation of hyperbola whose one focus in (4, 0 ) and corresponding equation of directrix x = 1 will be.
Answer:
- ± 4
- (0, \(\frac { – 5 }{ 2 }\))
- x2 + y2 – 4x – 4y – 5 = 0
- 7, 5
- ± 4
- (1, 2)
- x2 = 12y
- 6
- \(\frac { \sqrt { 3 } }{ 2 }\)
- \(\frac { x^{ 2 } }{ 4 } -\frac { y^{ 2 } }{ 12 } \) = 1
Conic Sections Long Answer Type Questions
Question 1.
Find the equation of circle which touches the X – axis at a distance of 4 units in the negative direction and makes intercept of 6 units on positive direction of Y – axis.
Solution:
Here OA = CM = 4, BD = 6.
Length of perpendicular drawn from centre C on BD.
Then, BM = MD = 3
In right angled ∆ CMB,
CB2 = CM2 + BM2
= 42 + 32
= 16 + 9 =25
⇒ CB = 5
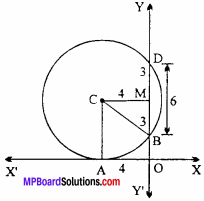
∴ CA = Radius of circle = CB = 5
∴ Centre of circle (- 4, 5) and radius = 5
Hence, equation of circle :
(x + 4)2 + (y – 5)2 = 52
⇒ x2 + 8x + 16 + y2 – 10y + 25 = 25
⇒ x2 + y2 + 8x – 10y + 16 = 0
Question 2.
Find the equation of circle which touches Y – axis at a distance of 4 units and makes intercept of 6 units on Y – axis?
Solution:
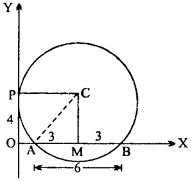
Given : OP = 4, AB = 6, PC = AC = radius.
CM ⊥ AB ∴ AM = BM = \(\frac { 6 }{ 2 }\) = 3
OP = CM = 4
In right angled ∆ AMC,
AC2 = AM2 + CM2
= (3)2 + (4)2 = 9 + 16 = 25
∴ AC = 5
From figure PC – OM= 5 = radius
Centre of circle is (5, 4) and radius = 5.
Hence, required equation of circle :
(x – 5)2 + (y – 4)2 = (5)2
x2 – 10x + 25 + y2 – 8y + 16 = 25
x2 + y2 – 10x – 8y + 16 = 0.
Question 3.
ABCD is a square. Supposing AB and AD as the coordinate axes. Find the equation of the circle circumscribing the square if each side of square is of length l.
Solution:
Taking AB and AD as X – axis and Y – axis respectively
Given : AB = BC = CD = DA = 1
M is mid point of AB.
N is mid point of AD.
AM = \(\frac { l }{ 2 }\), AN = \(\frac { l }{ 2 }\) = OM
In ∆OAM,
OA2 = AM2 + OM2
= \(\frac { l }{ 2 }\)2 + \(\frac { l }{ 2 }\)2
= \(\frac{l^{2}}{4}+\frac{l^{2}}{4} = \frac{l^{2}}{2}\)
∴ Radius = OA = \(\frac{l}{\sqrt{2}}\)
Centre of circle (AM, OM) = ( \(\frac { l }{ 2 }\), \(\frac { l }{ 2 }\) )
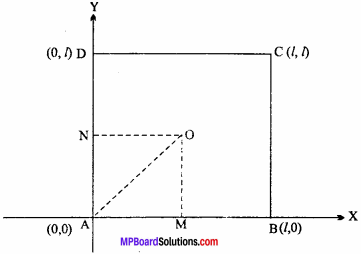
Required equation of circle is :
(x – \(\frac { l }{ 2 }\) )2 + (y – \(\frac { l }{ 2 }\) )2 = \(\frac{l^{2}}{2}\)
Centre of circle (AM, OM) = (\(\frac { l }{ 2 }\), \(\frac { l }{ 2 }\))
Required equation of circle is :
(x – \(\frac { l }{ 2 }\))2 + (y – \(\frac { l }{ 2 }\))2 = \(\frac{l^{2}}{2}\)
⇒ x2 – lx + \(\frac{l^{2}}{4}\) + y2 – ly + \(\frac{l^{2}}{4}\) = \(\frac{l^{2}}{2}\)
⇒ x2 + y2 – l(x + y) = 0
⇒ x2 + y2 = l(x + y)
![]()
Question 4.
Find the equation of the circle passing through the points (4, 1) and (6, 5). Whose centre lies on line 4x + y = 16. (NCERT)
Solution:
Let the equation of circle be
x2 + y2 + 2gx + 2 fy + c = 0 …. (1)
It passes through points (4, 1) and (6, 5).
∴ 8g + 2f + c + 17 = 0 …. (2)
and 12g + 10f + c + 61 = 0 …. (3)
Centre of circle (1) is (- g, – f) which lies on line 4x + y = 16.
∴ – 4g – f – 16 = 0
⇒ 4g + f + 16 – 0 …. (4)
Subtracting equation (2) from equation (3), we get
4g + 8f + 44 = 0
⇒ g + 2f + 11 = 0 …. (5)
On solving equation (4) and (5), g = – 3, f = – 4
Put g = – 3 and f = – 4 in equation (2),
– 24 – 8 + C + 17 = 0
⇒ c = 15
Put values of g, f and c in equation (1), then required equation of circle is :
x2 + y2 – 6x – 8y + 15 = 0.
Question 5.
Find the equation of the circle which passes through the points (2, 3) and (- 1, 1) whose centre lies on line x – 3y – 11 = 0. (NCERT)
Solution:
Let the equation of circle is :
x2 + y2 + 2gx + 2fy + c = 0 …. (1)
∵Points (2, 3) and (- 1, 1) lies on equation (1),
∴ (2)2 + (3)2 + 2g(2) + 2f(3) + c = 0
⇒ 4 + 9 + 4g + 6f + c + 13 = 0
4g + 6f + c + 13 = 0 …. (2)
and (-1)2 + (l)2 – 2g + 2f + c = 0
⇒ 1 + 1 – 2g + 2f + c = 0
⇒ – 2g + 2f + c + 2 = 0 …. (3)

Putting the value of g, f and c in equation (1), then required equation of circle will be :
x2 + y2 + 2(\(\frac { -7 }{ 2 }\))x + 2(\(\frac { 5 }{ 2 }\))y + c = 0 …. (1)
x2 + y2 – 7x + 5y -14 = 0.
Question 6.
Find the equation of circle whose radius is 5, centre is on Y – axis and which passes through point (2, 3).
Solution:
Centre of circle is on X – axis, so k = 0.
Let the equation of circle be :
(x – h)2 + (y – k)2 = a2
Here a = 5
(x – h)2 + (y – 0)2 = (5)2
(x – h)2 + y2 = 25
Circle (1) passes through point (2, 3),
∴ (2 – h)2 + (3)2 = 25
⇒ (2 – h)2 = 25 – 9 = 16 = (4)2
⇒ 2 – h = ± 4

Question 7.
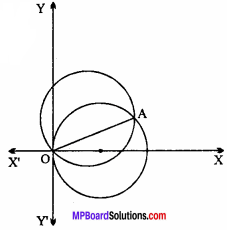
y = mx is a chord of the circle whose radius is ‘a’ and its diameter is X – axis. Origin is one of the limiting points of the chord. Show that the equation to a circle whose diameter is the given chord is given by the equation (1 + m2) (x2 + y2 ) – 2a (x + my) = 0. Solution:
Equation of circle whose radius is a and centre is (a, 0) will be
(x – a)2 + y2 = a2
⇒ x2 – 2ax + y2 + a2 = a2
⇒ x2 – 2ax + y2 = 0 …. (1)
Equation of given line is :
y = mx …. (2)
Now, equation of circle passing through the intersection of eqns. (1) and (2) will be :
x2 + y2 – 2ax + λ(y – mx) = 0 … (3)
Centre of co – ordinate of circle (3) are (\(\frac { λm + 2a }{ 2 }\), \(\frac { λ }{ 2 }\))
∵ Centre lies on line y = mx.
∴ – \(\frac { λ }{ 2 }\) = m\(\frac { λm + 2a }{ 2 }\)
⇒ λ = \(\frac{-2 a m}{1+m^{2}}\)
Put the value of λ in Equation (3),
x2 + y2 – 2ax + \(\frac{-2 a m}{1+m^{2}}\) (y – mx) = 0
⇒ (l + m2)(x2 + y2) = 2ax + 2am2x + 2amy – 2am2x
⇒ (l + m2)(x2 + y2) = 2a(x + my)
⇒ (l + m2)(x2 + y2) – 2a(x + my) = 0
Which is required equation of circle.
Question 8.
If the straight line x cos α + y sin α = p cuts a circle x2 + y2 = a2 in two points M and N, then show that the equation of the circle whose diameter is MN will be x2 + y2 – a2 = 2p(x cos α + y sin α – p).
Solution:
Given : Equation of line is :
x cos α + y sin α = p …. (1)
and Equation of circle is
x2 + y2 = a2 …. (2)
Now, equation of circle passing through the intersection of line (1) and circle (2) at points M and N is :
x2 + y2 – a2 + λ(x cos α + y sin α – p) = 0 …. (3)
If MN is diameter of above circle then centre is :
(- \(\frac { λ }{ 2 }\)cos α, – \(\frac { λ }{ 2 }\)sin α)
Which is lies on line x cos α + y sin α = p.
– ( \(\frac { λ }{ 2 }\)cos α )cos α + (- \(\frac { λ }{ 2 }\)sin α)sin α = p
⇒ – \(\frac { λ }{ 2 }\)[cos2 α + sin2 α] = p
⇒ λ = – 2p
Put the value of λ in equation (3), then required equation of circle is
x2 + y2 – a2 – 2p(x cos α + y sin α – p) = 0
⇒ x2 + y2 – a2 = 2p(x cos α + y sin α – p)
![]()
Question 9.
Find the following equation of parabola : (i) co – ordinates of focus, (ii) axis, (iii) equation of directrix, (iv) length of Iatus rectum. (NCERT)
(A) y2 = 12x
Solution:
Equation of parabola : y2 = 12x
Comparing with y2 = 4 ax,
4a = 12 ⇒ a = 3
∴Co – ordinates of focus (a, 0) = (3, 0).
Axis of parabola = X – axis.
Equation of directrix is x = – a ⇒ x = – 3.
Length of latus rectum = 4a = 4 x 3 = 12.
(B) x2 = 6y.
Solution:
Equation of parabola: x2 = 6y
Comparing with x2 = 4ay
4a = 6 a ⇒ 3/2
∴ Co – ordinate of focus (0, a) = (0, 3/2).
Axis of parabola = Y – axis.
Equation of directrix is y = – a ⇒ y = – 3/2.
(C) y2 = – 8x
Solution:
Equation of parabola : y2 = – 8x
Comparing with y2 = – 4ax
– 4a – = – 8 ⇒ a = 2
∴ Co – ordinates of focus (- a, 0) = (- 2, 0).
Axis of parabola = X – axis.
Equation of directrix is x = a ⇒ x = 2.
Length of latus rectum 4a = 4 x 2 = 8.
(D) x2 = – 16y
Solution:
Equation of parabola : x2 = – 16y
Comparing with x2 = – 4ay
– 4a = – 16 ⇒ a = 4
∴ Co – ordinate of focus (0, – a) = (0, – 4)
Axis of parabola = Y – axis
Equation of directrix is y = a ⇒ y = 4
Length of latus rectum = 4a = 16.
Question 10.
An equilateral triangle inscribed in the parabola y2 = 4ax, where one vertex is at the vertex of parabola. Find the length of the side of triangle. (NCERT)
Solution:
Let the equation of parabola is y2 = 4ax.
Let APQ be the equilateral triangle whose vertex A(0, 0), P(h, k) and Q(h, – k).
AP2 = (h – 0)2 + (k – 0)2
= h2 + k2
⇒ AP = \(\sqrt{h^{2}+k^{2}}\)
Similarly, AQ = \(\sqrt{h^{2}+k^{2}}\)
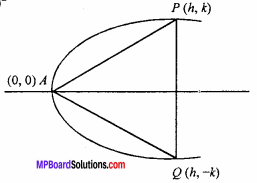
Again, PQ = \(\sqrt{(h-k)^{2}+(k+h)^{2}}\)
= \(\sqrt{(2k)^{2}}\) = 2k
∴ AP = PQ
⇒ \(\sqrt{h^{2}+k^{2}}\) = 2k
⇒ h2 + k2 = 4k2
⇒ h2 = 3k2
⇒ h = \(\sqrt {3}\).k
∵ Point P(h, k) lies on parabola y2 = 4ax.
k2 = 4ah = 4a.\(\sqrt {3}\)k
⇒ k = 4a\(\sqrt {3}\), [∵ k ≠ 0]
Hence, length of side PQ = 2k = 2.(4a\(\sqrt {3}\)) = 8a\(\sqrt {3}\).
Question 11.
If a parabola reflector is 20 cm in diameter and 5 cm deep. Find the focus. (NCERT)
Solution:
Taking vertex of parabola reflector at origin and X – axis along the axis of parabola.
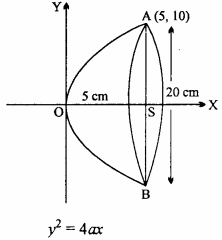
Equation of parabola y2 = 4ax …. (1)
Given : OS = 5 cm, AB = 20 cm, AS = 10 cm
∴ Co – ordinate of A will be (5, 10).
∴ (10)2 = 4a x 5
⇒ 100 = 20a
⇒ a = 5
∴ OS = 5 cm
Co – ordinates of focus S will be (5, 0).
Question 12.
An arch is in the form of a parabola with its vertical axis. The arch is 10 m high and 5 m wide at the base. How wide it is 2 m vertex of the parabola. (NCERT)
Solution:
Let the equation of parabola is :
x2 = 4 ay …. (1)
Given : AB = 5 metre
AF = BF = \(\frac { 5 }{ 2 }\) metre
OE = 2 metre
OF = 10 metre
Co – ordinate of A will be (\(\frac { 5 }{ 2 }\), 10)
This point lies on parabola, hence it will be satisfy equation (1),
∴ \(\frac { 5 }{ 2 }\)2 = 4a x 10
⇒ \(\frac { 25 }{ 4 }\) = 4 x a x 10
⇒ a = \(\frac { 25 }{ 4 × 4 × 10 }\)
⇒ a = \(\frac { 5 }{ 32 }\)
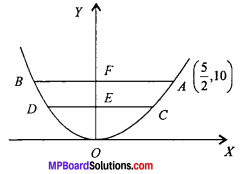
Put the value of a in Equation (1),
∴ x2 = 4 x \(\frac { 5 }{ 32 }\)y
⇒ x2 = \(\frac { 5 }{ 8 }\)y
Let EC = k
OE = 2
Co – ordinate of C will be (k, 2) and it will satisfy equation of parabola.
We get k2 =\(\frac { 5 }{ 8 }\) x 2
⇒ k2 = \(\frac { 5 }{ 4 }\)
⇒ k = \(\frac{\sqrt{5}}{2}\)
DE = 2EC
2 x \(\frac{\sqrt{5}}{2}\) = \(\sqrt {5}\)
= 2.23 metre (approx.)
Question 13.
In each of the following ellipse. Find the co – ordinates of the foci and vertices, the length of major axis and minor axis, the eccentricity and the length of latus rectum of the ellipse. (NCERT)
(A) = \(\frac{x^{2}}{36}+\frac{y^{2}}{16}\) = 1.
Solution:
Comparing with standard form of ellipse, \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
We get, a2 = 36 ⇒ a = 6, b2 = 16 ⇒ b = 4
Here a > b.
∴ b2 = a2(1 – e2)
⇒ 16 = 36(1 – e2)
⇒ 1 – e2 = \(\frac { 16 }{ 36 }\) = \(\frac { 4 }{ 9 }\)
⇒ e2 = 1 – \(\frac { 4}{9 }\) = \(\frac { 5 }{ 9 }\)
∴ Eccentricity e = \(\frac{\sqrt{5}}{3}\)
Foci (± ae, o) = (± 6 × \(\frac{\sqrt{5}}{3}\), o)
= (± 2\(\sqrt {5}\), 0)
Vertices (± a, 0) = (± 6, 0)
Length of major axis = 2a = 2 x 6 = 12.
Length of minor axis = 2b = 2 x 4 = 8.
Length of latus rectum = \(\frac{2 b^{2}}{a}\) = \(\frac { 2 × 16 }{ 6 }\) = \(\frac { 16 }{ 3 }\).
(B) \(\frac{x^{2}}{4}+\frac{y^{2}}{25}\) = 1.
Solution:
Comparing with standard form of ellipse, \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
We get, a2 = 36 ⇒ a = 6, b2 = 16 ⇒ b = 4
Here a < b.
∴ a2 = b2(1 – e2)
⇒ 4 = 25(1 – e2)
⇒ 1 – e2 = \(\frac { 4 }{ 25 }\)
⇒ e2 = 1 – \(\frac { 4}{25 }\) = \(\frac { 21 }{ 25 }\)
∴ Eccentricity e = \(\frac{\sqrt{21}}{5}\)
Foci (0, ± b) = (0, ± 5 × \(\frac{\sqrt{21}}{5}\))
= (0, ± \(\sqrt {21}\))
Vertices (0, ± b) = (0, ± 5)
Length of major axis = 2b = 2 x 5 = 12.
Length of minor axis = 2a = 2 x 2 = 8.
Length of latus rectum = \(\frac{2 a^{2}}{b}\) = \(\frac{2 \times 2^{2}}{5}\) = \(\frac { 2 × 4 }{ 5 }\) = \(\frac { 8 }{ 5 }\).
Question 14.
Find the equation of hyperbola whose foci is (± 4, 0) and length of latus rectum is 12. (NCERT)
Solution:
Foci of hyperbola (± 4, 0).
Hence equation of hyperbola will be :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1
Foci (±ae, 0) = (± 4, 0)
∴ ae = 4
Length of latus rectum = \(\frac{2 b^{2}}{a}\) = 12
⇒ b2 = 6a
We know, b2 = a2(e2 – 1)
⇒ 6a = a2e2 – a2
⇒ 6a = 42 – a2
⇒ 6a = 16 – a2
⇒ 6a = 16 – a2
⇒ a2 + 6a – 16 = 0
⇒ a2 + 8a – 2a – 16 = 0
⇒ a(a – 2)(a + 8) = 0
⇒ a = 2, a = – 8, (∵ a cannot be negative)
∴ a = 2
b2 = 6a = 6 x 2 = 12
⇒ b = \(\sqrt {12}\)
Putting values of a and b in equation (1), then required equation of hyperbola will be :
\(\frac{x^{2}}{2^{2}}-\frac{y^{2}}{(\sqrt{12})^{2}}\) = 1
⇒ \(\frac{x^{2}}{4}+\frac{y^{2}}{12}\) = 1
⇒ 3x2 – y2 = 12.
Question 15.
Find the axis, foci, directrix, eccentricity and the latus rectum of the ellipse 9x2 + 4y2 = 36.
Solution:
Given equation of ellipse
9x2 + 4y2 = 36
⇒ \(\frac{x^{2}}{4}+\frac{y^{2}}{9}\) = 1
Here, b2 > a2 or b > a
∴ Major axis = 2.3 = 6
Minor axis = 2.2 = 4
Now,
a2 = b2(1 – e2)
(2)2 = (3)2(1 – e2)
⇒ 4 = 9(1 – e2)
⇒ \(\frac { 4 }{ 9 }\) = 1 – e2
⇒ e2 = 1 – \(\frac { 4 }{ 9 }\) = \(\frac { 9 – 4 }{ 9 }\) = \(\frac { 5 }{ 9 }\)
∴ e = \(\frac{\sqrt{5}}{3}\)
Co – ordinate of foci = (0, ± be )
= (0, ± 3. \(\frac{\sqrt{5}}{3}\))
= (0, ± \(\sqrt {5}\)).
Co – ordinate of vertex = (0, ± b )
= (0 ± 3 ).
Length of latus rectum = \(\frac{2 a^{2}}{b}\)
= \(\frac { 2.4 }{ 3 }\) = \(\frac { 8 }{ 3 }\).
![]()
Question 16.
(A) Find the equation of ellipse whose vertices are (± 5, 0) and foci (± 4, 0).
Solution:
Given : Vertices are (± 5, 0) and foci are (± 4, 0)
∴ a = 5
and ae = 4
⇒ 5e = 4
⇒ e = \(\frac { 4 }{ 5 }\)
Let the equation of ellipse is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1, where a > b …. (1)
∴ From b2 = a2(1 – e2),
b2 = 52(1 – (\(\frac { 4 }{ 5 }\))2)
b2 = 25(1 – \(\frac { 16 }{ 25 }\))
b2 = 25 x \(\frac { 9 }{ 25 }\) = 9
Putting values of a and b in equation (1), the required equation of ellipse will be :
\(\frac{x^{2}}{25}+\frac{y^{2}}{9}\) = 1
⇒ 9x2 + 25y2 = 225
(B) Find the equation of ellipse whose vertices are (0, ± 13) and foci is (0, ± 5).
Solution:
Let the equation of ellipse is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1, where a < b …. (1)
Vertices of ellipse = (0, ± b) = (0, ± be)
∴ b = 13
Foci = (0, ± 5) = (0, ± be)
∴ be = 15
⇒ 13 x 3 = 5
⇒ e = \(\frac { 5 }{ 13 }\)
Now, a2 = b2(1 – e2)
⇒ a2 = 132[1 – ( \(\frac { 5 }{ 13 }\))2 ]
⇒ a2 = 169[1 – \(\frac { 25 }{ 169 }\) ]
⇒ a2 = 169\(\frac { 169 – 25 }{ 169 }\)
⇒ a2 = 144
⇒ a = 12.
Putting values of a and b in equation (1), then required equation of ellipse will be :
\(\frac{x^{2}}{(12)^{2}}-\frac{y^{2}}{(13)^{2}}\) = 1
⇒ \(\frac{x^{2}}{144}+\frac{y^{2}}{169}\) = 1
Question 17.
Find the equation of ellipse whose centre is at (0, 0), major axis on the Y – axis passing through the points (3, 2) and (1, 6).
Solution:
Let the equation of ellipse is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1, where a < b …. (1)
∵ Equation (1) passes through points(3, 2) and (1, 6)
∴ \(\frac{9}{a^{2}}+\frac{4}{b^{2}}\) = 1 …. (2)
and \(\frac{1}{a^{2}}+\frac{36}{b^{2}}\) = 1 …. (3)
Multiply equation (2) by 9, we get

Putting value of a2 in equation (2), we get
\(\frac { 9 }{ 10 }\) + \(\frac{4}{b^{2}}\) = 1
⇒ \(\frac{4}{b^{2}}\) 1 – \(\frac { 9 }{ 10 }\)
⇒ \(\frac{4}{b^{2}}\) = \(\frac { 1}{ 10 }\)
⇒ b2 = 40
Putting values of a2 and b2 in equation (1), then required equation of ellipse will be :
\(\frac{x^{2}}{10}+\frac{y^{2}}{40}\) = 1
Question 18.
Find the equation of ellipse whose major axis on the X – axis which passes through the points (4, 3) and (6, 2).
Solution:
Let the equation of ellipse is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 …. (1)
∵ It passes through points(4, 3) and (6, 2)
∴\(\frac{36}{a^{2}}+\frac{4}{b^{2}}\) = 1 …. (2)
and \(\frac{16}{a^{2}}+\frac{9}{b^{2}}\) = 1 …. (3)
Subtracting equation (3) from equation (2), we get
\(\frac{20}{a^{2}}-\frac{5}{b^{2}}\) = 1
⇒ \(\frac{4}{a^{2}}-\frac{1}{b^{2}}\) = 1
⇒ \(\frac{4}{a^{2}} = \frac{1}{b^{2}}\)
⇒ a2 = 4b2
Putting value of a2 in equation (2), we get
\(\frac{36}{4b^{2}}+\frac{4}{b^{2}}\) = 1
⇒ \(\frac{9}{b^{2}}+\frac{4}{b^{2}}\) = 1
⇒ 9 + 4 = b2
⇒ b2 = 13
Putting values of a2 and b2 in equation (1), hence
Required equation of ellipse \(\frac{x^{2}}{52}+\frac{y^{2}}{13}\) = 1
Question 19.
An arch is the form of a semi ellipse. It is 8 m wide and 2 m high of the centre. Find the height of the arch at a point 1-5 m from one end. (NCERT)
Solution:
Let the equation of ellipse is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 …. (1)
Here 2a = 8 ⇒ a = 4, b = 2
Putting the values of a and b, we get
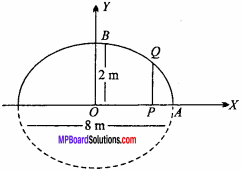
\(\frac{x^{2}}{4^{2}}-\frac{y^{2}}{2^{2}}\) = 1 …. (1)
\(\frac{x^{2}}{16}+\frac{y^{2}}{4}\) = 1
Given :
AP = 1.5m, OA = \(\frac { 8 }{ 2 }\) = 4m,
OP = OA – AP = 4 – 1.5 = 2.5m.
Let PQ = k
∴ Co – ordinate of Q will be (2.5, k), which will satisfy ellipse’s equation.
Hence,
\(\frac{(2.5)^{2}}{16}+\frac{k^{2}}{4}\) = 1
⇒ \(\frac { 6.25}{ 16 }\) + \(\frac{k^{2}}{4}\) = 1
⇒ \(\frac{k^{2}}{4}\) = 1 – \(\frac { 6.25 }{ 16 }\)
⇒ \(\frac{k^{2}}{4}\) = \(\frac { 16 – 6.25 }{ 16 }\)
⇒ k2 = \(\frac { 9.75 }{ 4 }\)
⇒ k2 = 2.437
⇒ k = 1.56metre (approx).
Question 20.
A rod of length 12 cm moves with its ends always touching the co – ordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with the X – axis. (NCERT)
Solution:
Let AB be the rod of length 12 cm which make an angle θ with X – axis.
∴ ∠BAO = θ
AB = 12 cm
AP = 3 cm, then PB = 9 cm
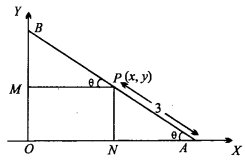
In ∆PNA,
sin θ = \(\frac {PN }{ PA }\) = \(\frac { y }{ 3 }\)
In ∆PMB,
cos θ = \(\frac { PM }{ PB }\) = \(\frac { x }{ 9 }\)
sin2θ + cos2θ = \(\frac { y }{ 3 }\)2 + \(\frac { x }{ 9 }\)2
⇒ 1 = \(\frac{y^{2}}{9}+\frac{x^{2}}{81}\)
Hence required equation is :
\(\frac{x^{2}}{81}+\frac{y^{2}}{9}\) = 1
Question 21.
Find the eccentricity, co – ordinate of foci, equation of directrix and length of Iatus rectum of ellipse 4x2 + y2 – 8x + 2y + 1 = 0.
Solution:
4x2 + y2 – 8x + 2y + 1 = 0
⇒ 4x2 – 8x + y2 + 2y +1 = 0
⇒ 4x2 – 8x + (y + 1)2 = 0
⇒ 4(x2 – 2x) + (y + 1)2 = 0
⇒ 4(x2 – 2x + 1) + (y + 1)2 = 4
⇒ 4(x2 – 2x + 1) + (y + 1)2 = 4
⇒ \(\frac{(x-1)^{2}}{1}+\frac{(y+1)^{2}}{4}\) or \(\frac{X^{2}}{1}+\frac{Y^{2}}{4}\) = 1
Here, b > a
a2 = b2(1 – e2)
⇒ 1 = (1 – e2)
⇒ \(\frac { 1 }{ 4}\) = 1 – e2
⇒ e2 = 1 – \(\frac { 1 }{ 4}\) = \(\frac { 3 }{ 4}\)
⇒ Eccentricity e = \(\frac{\sqrt{3}}{2}\)
Co – ordinate of foci (0, ± be)
= (0, ±2. \(\frac{\sqrt{3}}{2}\)
= (0, ± \(\sqrt {3}\) )
Here X = 0, Y = ± \(\sqrt {3}\)
∴ x – 1 = 0, y + 1 = ± \(\sqrt {3}\)
⇒ x = 1, y = – 1 ± \(\sqrt {3}\)
foci = (1 ± \(\sqrt {3}\) – 1)
Equation of directrix Y = ± \(\frac { b }{ e}\)
⇒ Y = ± \(\frac{2}{\sqrt{3}}\).2
⇒ Y = ± \(\frac{4}{\sqrt{3}}\)
Y + 1 = \(\frac{4}{\sqrt{3}}\), (∵ Y = y+1)
⇒ y = ± \(\frac{4}{\sqrt{3}}\) – 1
Length of latus rectum = \(\frac{2 a^{2}}{b}\)
= 2. \(\frac { 1 }{ 2 }\) = 1.
![]()
Question 22.
Find the vertices, co-ordinate of foci, eccentricity and length of latus rectum of hyperbola :
(A) 9y2 – 4x2 = 36.
Solution:
Given : 9y2 – 4x2 = 36
⇒ \(\frac{9 y^{2}}{36}-\frac{4 x^{2}}{36}\) = 1
⇒ \(\frac{y^{2}}{4}-\frac{x^{2}}{9}\) = 1
Comparing the above equation with the standard form of hyperbola
\(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}\) = 1 …. (1)
b2 = 4 ⇒ b = 2, a2 = 9 ⇒ a = 3
Let e is the eccentricity of hyperbola.
Then, a2 = b2(e2 – 1)
⇒ 9 = (e2 – 1)
⇒ \(\frac { 9 }{ 4 }\) = e2 – 1
⇒ e2 = \(\frac { 9 }{ 4 }\) + 1 = \(\frac { 13 }{ 4 }\)
∴ Eccentricity e = \(\frac{\sqrt{3}}{2}\)
Vertices = (0, ± b) = (0, ± 2)
Foci = (0, ± be) = (0, ± 2 x \(\frac{\sqrt{3}}{2}\)) = (0, ±\(\sqrt {3}\))
Length of latus rectum = \(\frac{2 a^{2}}{b}\) = \(\frac { 2 x 9 }{ 2 }\) = 9
(B) 16x2 – 9y2 = 576.
Solution:
Given : 16x2 – 9y2 = 576
⇒ \(\frac{16 x^{2}}{576}-\frac{9 y^{2}}{576}\) = 1
⇒ \(\frac{x^{2}}{36}-\frac{y^{2}}{64}\) = 1
Comparing the above equation with the standard form of hyperbola
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 …. (1)
Here, a2 = 36 ⇒ a = 6, b2 = 64 ⇒ b = 3
We Know that, b2 = a2(e2 – 1)
64 = 36(e2 – 1)
⇒ \(\frac { 64 }{ 36 }\) = e2 – 1
⇒ \(\frac { 16 }{ 9 }\) = e2 – 1
⇒ e2 = \(\frac { 16 }{ 9 }\) + 1 = \(\frac { 25 }{ 9 }\)
∴ Eccentricity e = \(\frac{5}{3}\)
Vertices = (± a, 0) = (± 6, 0)
Foci = (± ae, 0) = (± 6 x \(\frac { 5 }{ 3 }\)) = (± 10, 0)
Length of latus rectum = \(\frac{2 b^{2}}{a}\) = \(\frac { 2 x 64 }{ 6 }\) = \(\frac { 64 }{ 3 }\).
(c) 5y2 – 9x2 = 36.
Solution:
Given : 5y2 – 9x2 = 36
⇒ \(\frac{5 y^{2}}{36}-\frac{9 x^{2}}{36}\) = 1
\(\frac{y^{2}}{\frac{36}{5}}-\frac{x^{2}}{4}\) = 1
Comparing the above equation with the standard form of hyperbola
\(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}\) = 1 …. (1)
Here b2 = \(\frac { 36 }{ 5 }\) ⇒ b = \(\frac{\sqrt{6}}{5}\), a2 = 4 ⇒ a = 2
We know that, a2 = b2(e2 – 1)
⇒ 4 = \(\frac{\sqrt{36}}{5}\)(e2 – 1)
⇒ e2 – 1 = \(\frac { 20 }{ 36 }\) = \(\frac { 5 }{ 9 }\)
⇒ e2 = 1 + \(\frac { 5 }{ 9 }\) = \(\frac { 14 }{ 9 }\)

Question 23.
Find the equation of hyperbola whose foci are (0, ± \(\sqrt {10}\)) and which passes through point (2,3).
Solution:
Foci of hyperbola are (0, ±\(\sqrt {10}\)).
∴Form of hyperbola is :
\(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}\) = 1 …. (1)
Foci (0, ± be) = (0, ± \(\sqrt {10}\))
be = \(\sqrt {10}\)
Equation (1) passes through point (2, 3).
∴ \(\frac{9}{b^{2}}-\frac{4}{a^{2}}\)
⇒ 9a2 – 4b2 = a2b2
We know that, a2 = b2 (e2 – 1)
⇒ a2 = b2e2 – b2
a2 = ( \(\sqrt {10}\))2 – b2
⇒ a2 = 10 – b2
⇒ b2 = 10 – a2
Putting value of b2 in equation (2),
9a2 – 4(10 – a2) = a2 (10 – a2)
⇒ 9a2 – 40 + 4a2 = 10a2 – a4
⇒ 13a2 – 40 = 10a2 – a4
⇒ a4 + 13a2 – 10a2 – 40 = 0
⇒ a4 + 3a2 – 40 = 0
⇒ a4 + 8a2 – 5a2 – 40 = 0
⇒ a2(a2 + 8) – 5(a2 + 8) = 0
⇒ (a2 – 5)(a2 + 8) = 0
a2 = 5, a2 = – 8
∵ The value of a cannot be negative.
∴ a2 = 5
b2 = 10 – a2
⇒ b2 = 10 – 5
⇒ b2 = 5
Putting values of a2 and b2 in equation (1), then required equation of hyperbola will be :
\(\frac{y^{2}}{5}-\frac{x^{2}}{5}\) = 1
⇒ y2 – x2 = 5.
Question 24.
Find the equation of hyperbola in which the distance between foci is 8 and distance between directrix is 6.
Solution:
Let the equation of hyperbola is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) … (1)
and Eccentricity of hyperbola is e and foci are (ae, 0) and (- ae, 0) and latus rectum
are x = \(\frac { a }{ e }\) and x = – \(\frac { a }{ e }\)
Distance between foci = 2ae
Distance between latus rectum = \(\frac { 2a }{ e }\)
According to question, 2ae = 8
and \(\frac { 2a }{ e }\) = 6
Multiplying equation (2) and (3),
4a2 = 48 ⇒ a2 = 12
⇒ a = 2\(\sqrt {3}\)
Putting value of a in equation (2),
2.2\(\sqrt {3}\)e = 8 ⇒ e = \(\frac{2}{\sqrt{3}}\)
b2 = a2(e2 – 1)
= 12( \(\frac { 4 }{ 3 }\) – 1) = 4
Putting values of a2 and b2 in equation (1), the required equation of hyperbola is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\)
⇒ x2 – 3y2 = 12.
Question 25.
Find the centre, eccentricity, foci and length of latus rectum of hyperbola 9x2 – 16y2 + 18x + 32y – 151 = 0.
Solution:
Equation of hyperbola is :
9x2 – 16y2 + 18x + 32y – 151 = 0
⇒ 9x2 + 18x – 16y2 + 32y = 151
⇒ 9(x2 + 2x) – 16(y2 – 2y) = 151
⇒ 9(x + 1)2 – 16(y – 1)2 = 151 – 16 + 9
⇒ 9(x + 1)2 – 16(y – 1)2 = 144
⇒ \(\frac{9(x+1)^{2}}{144}-\frac{16(y-1)^{2}}{144}\)
⇒ \(\frac{(x+1)^{2}}{16}-\frac{(y-1)^{2}}{9}\) = 1
Let x + 1 = X and y – 1 = Y, then equation of hyperbola is
\(\frac{X^{2}}{16} – \frac{Y^{2}}{9}\) = 1
∴ a2 = 16 ⇒ a = 4 and b2 = 9 ⇒ b = 3.
∴ Centre is (- 1, 1).
For eccentricity = e
b2 = a2(e2 – 1)
⇒ 9 = 16(e2 – 1)
⇒ \(\frac { 9 }{ 16 }\) = e2 – 1
⇒ e2 = 1 + \(\frac { 9 }{ 16 }\) = \(\frac { 25 }{ 16 }\)
⇒ e = \(\frac { 5 }{ 4 }\)
For foci, X = ± ae, Y = 0
⇒ x +1 = ± 4 x \(\frac { 5 }{ 4 }\), y – 1 = 0
⇒ x + 1 = ± 5, y = 1
⇒ x = 4, – 6, y = 1
∴ Foci are (4, 1) and (6, 1).
Equation of directrix is X = ± \(\frac { a }{ e }\)
⇒ x +1 = ± \(\frac { 4 }{ 5/4 }\)
⇒ x = ± \(\frac { 16 }{ 5 }\) – 1
⇒ x = ± \(\frac { 11 }{ 5 }\) and x = – \(\frac { 21 }{ 5 }\)
⇒ 5x = 11 and 5x + 21 = 0.
![]()
Question 26.
If e and ex are the eccentricity of hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) and \(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}\) = 1, then prove that: \(\frac{1}{e^{2}}+\frac{1}{e_{1}^{2}}\) = 1.
Solution:
Equation of hyperbola is
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1
and
\(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}\) = 1
For eccentricity e of equation (1),
b2 = a2(e2 – 1)
⇒ \(\frac{b^{2}}{a^{2}}\) = (e2 – 1)
⇒ e 2 = 1 + \(\frac{b^{2}}{a^{2}}\) = \(\frac{a^{2}+b^{2}}{b^{2}}\)
⇒ \(\frac{1}{e_{1}^{2}}\) = \(\frac{a^{2}}{a^{2}+b^{2}}\)
Again for eccentricity e of equation (2),

Question 27.
On a level plain the crack of the rifle and the thud of the ball striking the target are heard at the same instant, prove that the locus of the hearer is a hyperbola.
Solution:
Let P be the situation of hearer and T be the situation of the rifle and S is target. Let the velocity of the ball be v1 and the velocity of sound be v2.
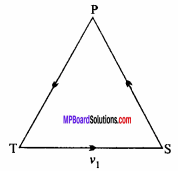
Then,
Time to reach the ball from T to S = \(\frac{T S}{v_{1}}\)
Time to reach the sound from S to P = \(\frac{S P}{v_{2}}\)
and Time to reach the sound from T to P = \(\frac{T P}{v_{2}}\)
∴ The crack of the rifle and the thud of the ball are heard at the same instant.
∴ \(\frac{T S}{v_{1}}\) + \(\frac{S P}{v_{2}}\) = \(\frac{T P}{v_{2}}\)
⇒ \(\frac{T P}{v_{2}}\) – \(\frac{S P}{v_{2}}\) = \(\frac{T S}{v_{1}}\)
⇒ TP – SP = \(\frac{v_{2}}{v_{1}}\)
⇒ PT – PS = A constant (∵ v2, v2, TS are constant)
Hence locus of point P is hyperbola whose foci is T and S.
MP Board Class 11th Maths Important Questions