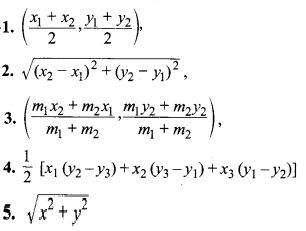MP Board Class 10th Maths Solutions Chapter 7 निर्देशांक ज्यामिति Additional Questions

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 7 निर्देशांक ज्यामिति Additional Questions Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 7 निर्देशांक ज्यामिति Additional Questions

MP Board Class 10th Maths Chapter 7 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 10th Maths Chapter 7 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
यदि बिन्दु A (k + 1, 2k), B (3k, 2k + 3) तथा C (5k – 1, 5k) सरेख हों तो k का मान ज्ञात कीजिए।
हल :
चूँकि A, B एवं C सरेख हैं
⇒ ar (ABC) = 0
⇒ \(\frac { 1 }{ 2 }\) [(k + 1) (2k + 3 – 5k)] + (3k) (5k – 2k) + (5k – 1) (2k – 2k – 3) = 0
⇒ (k + 1) (-3k + 3) + (3k) (3k) + (5k – 1) (-3) = 0
⇒ -3k² + 3k – 3k + 3 + 9k² – 15k + 3 = 0
⇒ 6k² – 15k + 6 = 0
⇒ 2k² – 5k + 2 = 0
⇒ 2k² – 4k – k + 2 = 0
⇒ 2k (k – 2) – 1 (k – 2) = 0
⇒ (k – 2) (2k – 1) = 0
या तो k – 2 = 0 ⇒ k = 2
अथवा 2k – 1 = 0 ⇒ k = \(\frac { 1 }{ 2 }\)
अत: k का अभीष्ट मान 2 या \(\frac { 1 }{ 2 }\) है।

प्रश्न 2.
k के मान ज्ञात कीजिए, जिससे (1, -1), (-4, 2k) तथा (-k, -5) शीर्षों वाले त्रिभुज का क्षेत्रफल 24 वर्ग इकाई है।
हल :
चूँकि त्रिभुज का क्षेत्रफल ∆ = 24 वर्ग इकाई (दिया है)
⇒ \(\frac { 1 }{ 2 }\) [1 (2k + 5) + (-4) (-5 + 1) + (-k)] (-1 – 2k)] = 24
⇒ [(2k + 5) + (-4) (-4) + (-k) (-2k – 1)] = 48
⇒ 2k + 5 + 16 + 2k² + k = 48
⇒ 2k² + 3k + 21 = 48
⇒ 2k² + 3k – 27 = 0
⇒ 2k² + 9k – 6k – 27 = 0
⇒ k(2k + 9) – 3(2k + 9) = 0
⇒ (2k + 9)(k – 3) = 0
या तो 2k + 9 = 0 ⇒ k = \(-\frac { 9 }{ 2 }\)
अथवा k – 3 = 0 ⇒ k = 3
अत: k के अभीष्ट मान = \(-\frac { 9 }{ 2 }\) अथवा 3 हैं।

प्रश्न 3.
संलग्न आकृति में एक त्रिभुज ABC के शीर्ष A (4, 6), B (1, 5) तथा C(7, 2) हैं। एक रेखाखण्ड DE भुजाओं AB तथा AC को क्रमशः बिन्दुओं D तथा E पर इस प्रकार काटता हुआ खींचा गया \(\frac{A D}{A B}=\frac{A E}{A C}=\frac{1}{3}\) है
∆ADE का क्षेत्रफल ज्ञात कीजिए तथा उसकी ∆ABC के क्षेत्रफल से तुलना कीजिए।
हल :

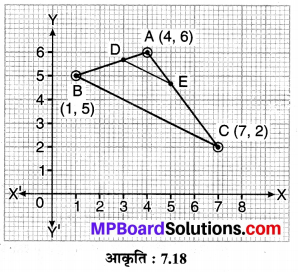
चूँकि \(\frac{A D}{A B}=\frac{A E}{A C}=\frac{1}{3}\) दिया है। अतः बिन्दु D एवं बिन्दु E रेखाखण्ड AB एवं AC को क्रमशः 1 : 2 के अनुपात में विभाजित करते हैं।

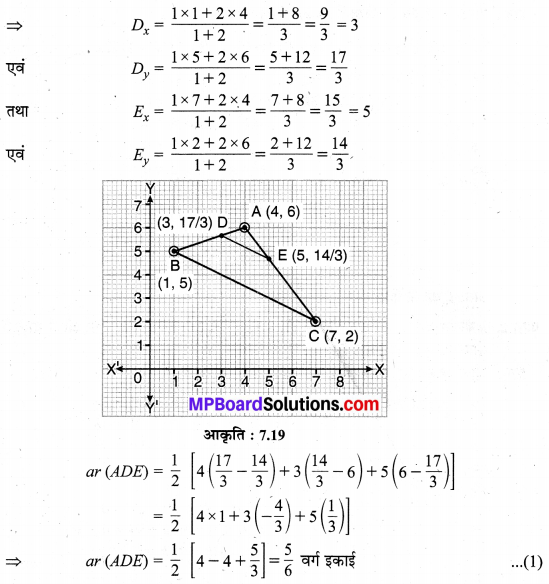
अत: त्रिभुज ADE का अभीष्ट क्षेत्रफल = \(\frac { 5 }{ 6 }\) वर्ग इकाई है।
अब ar (ABC) = \(\frac { 1 }{ 2 }\) [4 (5 – 2) + 1 (2 – 6) + 7 (6 – 5)]
= \(\frac { 1 }{ 2 }\) [4 (3) + 1 (-4) + 7 (1)]
⇒ ar (ABC) = \(\frac { 1 }{ 2 }\) [12 – 4 + 7]
= \(\frac { 15 }{ 2 }\) वर्ग इकाई …(2)
⇒ \(\frac { ar(ADE) }{ ar(ABC) } =\frac { \frac { 5 }{ 6 } }{ \frac { 15 }{ 2 } } =\frac { 1 }{ 9 } \)
अतः ∆ar (ADE) : ar (ABC) = 1:9 है।

प्रश्न 4.
बिन्दु (\(\frac { 24 }{ 11 }\), y), बिन्दुओं P (2, – 2), तथा Q (3, 7) को मिलाने वाले रेखाखण्ड को किस अनुपात में विभाजित करता है? y का मान भी ज्ञात कीजिए।
हल :
मान लीजिए बिन्दु (\(\frac { 24 }{ 11 }\), y) रेखाखण्ड PQ को m : 1 के अनुपात में विभाजित करता है, तो


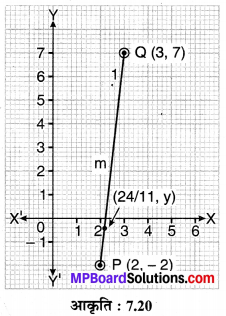
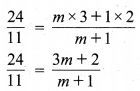
⇒ 33m + 22 = 24m + 24
⇒ 33m – 24m = 24 – 22
⇒ 9m = 2
⇒ m = \(\frac { 2 }{ 9 }\)
अतः अभीष्ट अनुपात = 2:9
अब

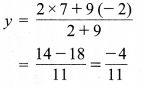
अतः y का अभीष्ट मान = \(\frac { -4 }{ 11 }\)

प्रश्न 5.
यदि बिन्दु P (x,y) बिन्दुओं A (a + b, b – a) तथा B (a – b, a + b) से समदूरस्थ है तो सिद्ध कीजिए bx = ay.
हल :

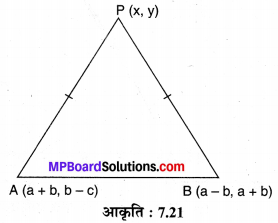
चूँकि PA = PB (दिया है)

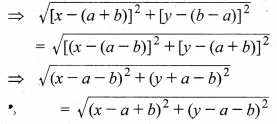
⇒ (x – a – b)² + (y + a – b)² = (x – a + b)² + (y – a – b)² दोनों ओर वर्ग करने पर।
⇒ x² + a + b² – 2xa + 2ab – 2xb + y² + a² + b² + 2ya – 2ab – 2yb
= x² + a² + b² – 2xa – 2ab + 2xb + y² + a² + b² – 2ya + 2ab – 2yb
⇒ x² + y² + 2a² + 2b² – 2ax – 2bx + 2ay – 2by
= x² + y² + 2a² + 2b² – 2ax + 2bx – 2ay – 2by
⇒ 4ay = 4bx
⇒ bx = ay
इति सिद्धम्

प्रश्न 6.
A (6, 1), B (8, 2) एवं C (9,4) समान्तर चतुर्भुज ABCD के तीन शीर्ष हैं, तथा E रेखाखण्ड DC का मध्य-बिन्दु है, तो ∆ADE का क्षेत्रफल ज्ञात कीजिए।
हल :
A (6, 1), B (8, 2) एवं C (9, 4) एक समान्तर चतुर्भुज के शीर्ष दिए हैं तथा E बिन्दु, रेखाखण्ड DC का मध्य-बिन्दु है।
ar (∆ADE) ज्ञात करना है।
चूँकि ABCD एक समान्तर चतुर्भुज है
ar (ABC) = ar (ACD) …(1) [विकर्ण समद्विभाजित करते हैं।
चूँकि AE, ∆ACD की माध्यिका है [E, DC का मध्य-बिन्दु है]
ar (ADE) = \(\frac { 1 }{ 2 }\) ar (ACD) ….(2)
ar (ADE) = \(\frac { 1 }{ 2 }\) ar (ABC) [समीकरण (1) व (2) से]
ar (ADE) = \(\frac{1}{2} \times \frac{1}{2}\) [6(2 – 4) + 8 (4 – 1) +9 (1 – 2)]
= \(\frac { 1 }{ 2 }\) [6 (-2) + 8 (3)] + 9 (-1)]
= \(\frac { 1 }{ 2 }\) [-12 + 24 – 9]

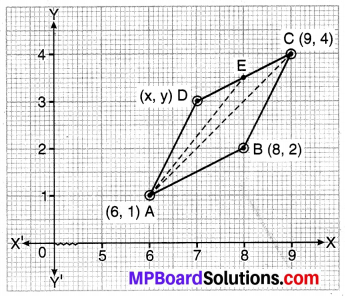
= \(\frac { 1 }{ 2 }\) [24 – 21]
= \(\frac { 3 }{ 4 }\) वर्ग इकाई
अत: ∆ADE का अभीष्ट क्षेत्रफल = \(\frac { 3 }{ 4 }\) वर्ग इकाई।

प्रश्न 7.
बिन्दु A (x₁, y₁), B (x₂, y₂) एवं C (x₃, y₃) ∆ABC के शीर्ष हैं, तो
(i) यदि A से खींची गयी माध्यिका BC से बिन्दु D पर मिलती है तो बिन्दु D के निर्देशांक ज्ञात कीजिए।
(ii) AD पर स्थित बिन्दु P के निर्देशांक ज्ञात कीजिए जबकि AP : PD = 2 : 1.
(iii) माध्यिका BE एवं CF पर बिन्दु Q एवं R इस प्रकार स्थित हैं कि BQ : QE = 2 : 1 तो Q एवं R के निर्देशांक ज्ञात कीजिए।
(iv) त्रिभुज ABC के केन्द्रक ज्ञात कीजिए।

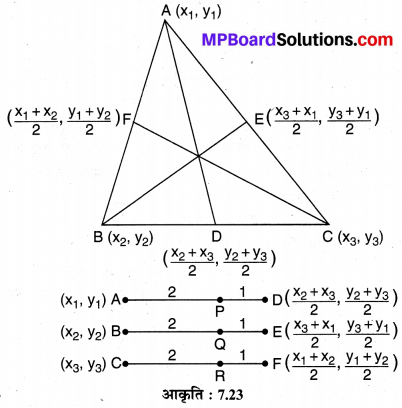
हल :
ज्ञात है ∆ABC की माध्यिकाएँ AD, BE एवं CF क्रमशः रेखाखण्ड BC, CA एवं AB के मध्य-बिन्दुओं क्रमश: D, E एवं F पर मिलती हैं। P, Q एवं R बिन्दु क्रमशः माध्यिकाओं AD, BE एवं CF को क्रमशः AP : PD = 2 : 1, BQ : QE = 2 : 1 एवं CR : RF = 2 : 1 के अनुपात में विभाजित करते हैं (देखिए आकृति 7.23)।
A (x₁, y₁), B (x₂, y₂) एवं C (x₃, y₃) निर्देशांक दिए हैं।
(i) चूँकि बिन्दु D रेखाखण्ड BC का मध्य-बिन्दु है।
D के निर्देशांक = \(\left(\frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2}\right)\)
अतः बिन्द D के अभीष्ट निर्देशांक = \(\left(\frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2}\right)\) हैं।

(ii) चूँकि बिन्दु P बिन्दु A (x₁, y₁) एवं D \(\left(\frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2}\right)\) को मिलाने वाले रेखाखण्ड को 2 : 1 के अनुपात में विभाजित करता है।

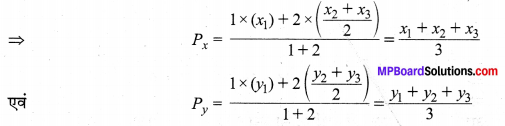
अत: P के अभीष्ट निर्देशांक = \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\) हैं।

(iii) बिन्दु E रेखाखण्ड CA का मध्य-बिन्दु है।
E के निर्देशांक = \(\left(\frac{x_{3}+x_{1}}{2}, \frac{y_{3}+y_{1}}{2}\right)\)
चूँकि बिन्दु F रेखाखण्ड AB का मध्य-बिन्दु है।
F के निर्देशांक = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
चूँकि बिन्दु , बिन्दु B (x₂, y₂) एवं E \(\left(\frac{x_{3}+x_{1}}{2}, \frac{y_{3}+y_{1}}{2}\right)\) को मिलाने वाली रेखा को 2 : 1 के अनुपात में विभाजित करता है।

अतः बिन्दु Q के अभीष्ट निर्देशांक = \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\) हैं।
चूँकि बिन्दु R बिन्दु C (x₃, y₃) एवं बिन्दु \(F\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\) को मिलाने वाली रेखा को 2 : 1 के अनुपात में विभाजित करता है।


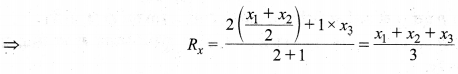
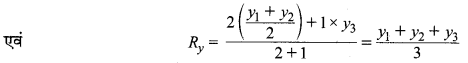
अतः बिन्दु R के अभीष्ट निर्देशांक = \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\) हैं।

(iv) ∆ABC के शीर्ष A (x₁, y₁), B (x₂, y₂) एवं C (x₃, y₃) हैं
∆ABC के केन्द्रक के निर्देशांक = \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\) (हम जानते हैं)
अत: ∆ABC के केन्द्रक के निर्देशांक = \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\) हैं।

MP Board Class 10th Maths Chapter 7 लघु उत्तरीय प्रश्न

प्रश्न 1.
यदि बिन्दु A (x, y), B (-5, 7) तथा C (-4, 5) सरेखीय हों, तो x तथा y में सम्बन्ध ज्ञात कीजिए।
हल :
चूँकि बिन्दु A, B तथा C सरेख हैं ⇒ ar (ABC) = 0
\(\frac { 1 }{ 2 }\) [x (7 – 5) + (-5) (5 – y) + (-4) (y – 7)] = 0
2x – 25 + 5y – 4y + 28 = 0
2x + y + 3 = 0
अतः x एवं y में अभीष्ट सम्बन्ध 2x + y + 3 = 0 है।

प्रश्न 2.
बिन्दु A (4, 7), B (p, 3) तथा C (7, 3) एक समकोण त्रिभुज के शीर्ष हैं, जिसमें B समकोण है। p का मान ज्ञात कीजिए।
हल :
चूँकि त्रिभुज ABC बिन्दु B पर समकोण है।
⇒ AB² + BC² = AC² [पाइथागोरस प्रमेय]
⇒ (p – 4)² + (3 – 7)² + (p – 7)² + (3 – 3)² = (4 – 7)² + (7 – 3)²
⇒ p² – 8p + 16 + 16 + p² – 14p + 49 + 0 = 9 + 16
⇒ 2p² – 22p + 56 = 0
⇒ p² – 11p + 28 = 0
⇒ p² – 4p – 7p + 28 = 0
⇒ p (p – 4) – 7 (p – 4) = 0
⇒ (p – 4) (p – 7) = 0
या तो p – 4 = 0 ⇒ p = 4
अथवा p – 7 = 0 ⇒ p = 7
अतः p का अभीष्ट मान या तो 4 है अथवा 7 है।

प्रश्न 3.
एक रेखा y-अक्ष तथा x-अक्ष को क्रमश: P तथा Q पर प्रतिच्छेद करती है। यदि (2, -5) PQ का मध्य-बिन्दु है, तो P तथा Q के निर्देशांक ज्ञात कीजिए।
हल :
चूँकि P, y-अक्ष का तथा Q, x-अक्ष का बिन्दु है तो मान लीजिए P(0, Y) तथा Q(x, 0) हैं।
चूँकि (2,-5) PQ का मध्य-बिन्दु हो, तो
\(\frac { x+0 }{ 2 }\) = 2
⇒ x = 4
⇒ Q (4,0)
एवं
\(\frac { y+0 }{ 2 }\) = -5
⇒ y = -10
⇒ P (0, -10)
अत: P एवं ए के अभीष्ट निर्देशांक क्रमशः P (0, – 10) एवं Q (4, 0) हैं।

प्रश्न 4.
यदि P (x, y) की A (5, 1) तथा B (-1, 5) से दूरियाँ समान हों तो सिद्ध कीजिए कि 3x = 2y.
हल :
चूँकि PA = PB दिया है
(PA)² = (PB)²
(x – 5)² + (y – 1)² = (x + 1)² + (y – 5)²
x² – 10x + 25 + y² – 2y + 1 = x² + 2x + 1 + y² – 10y + 25
-10x – 2x = – 10y + 2y
-12x = – 8y
3x = 2y.
इति सिद्धम्

प्रश्न 5.
सिद्ध कीजिए कि बिन्दु (3, 0), (6, 4) एवं (-1, 3) एक समकोण समद्विबाहु त्रिभुज के शीर्ष है|
हल :
मान लीजिए ∆PQR के शीर्ष P (3,0), Q (6, 4) एवं R (-1, 3) दिये हैं तो

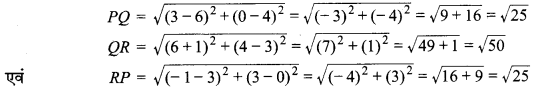
PQ = RP = √25
एवं PQ² + RP² = 25 + 25 = 50 = (√50)² = QR²
∆PQR समकोण समद्विबाहु त्रिभुज है।
अतः दिया हुआ ∆ समकोण समद्विबाहु त्रिभुज है।
इति सिद्धम्

प्रश्न 6.
बिन्दु A (-5, 6), B (-4,- 2) और C (7,5) से बने त्रिभुज का प्रकार (प्रकृति) बतलाइए।
हल :

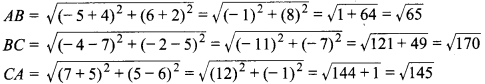
चैंकि AB ≠ BC ≠ CA
अतः दिया हुआ अभीष्ट ∆ABC विषमबाहु त्रिभुज है।

प्रश्न 7.
x-अक्ष पर वे बिन्दु ज्ञात कीजिए जो बिन्दु (7,-4) से 2√5 इकाई की दूरी पर हैं। इस प्रकार से कितने बिन्दु होंगे?
हल :
मान लीजिए अभीष्ट बिन्दु (x, 0) है (x-अक्ष पर y शून्य होता है) तो प्रश्नानुसार,
\(\sqrt{(x-7)^{2}+(0+4)^{2}}=2 \sqrt{5}\)
⇒ x² – 14x + 49 + 16 = 20 (दोनों ओर वर्ग करने पर)
⇒ x² – 14x + 45 = 0
⇒ x² – 5x – 9x + 45 = 0
⇒ x (x – 5) – 9 (x – 5) = 0
⇒ (x – 5) (x – 9) = 0
या तो x – 5 = 0 ⇒ x = 5
अथवा x – 9 = 0 ⇒ x = 9
अतः अभीष्ट दो बिन्दु क्रमशः (5,0) एवं (9,0) होंगे।

प्रश्न 8.
यदि बिन्दुओं A (-3, -14) एवं B (a, -5) के बीच की दूरी 9 इकाई है, तो a का मान ज्ञात कीजिए।
हल :
∵ AB = 9 (दिया है)
⇒ \(\sqrt{(a+3)^{2}+(-5+14)^{2}}=9\)
⇒ a² + 6a + 9 + 81 = 81 (दोनों ओर वर्ग करने पर)
⇒ a² + 6a + 9 = 0
⇒ (a + 3)² = 0
⇒ a + 3 = 0
⇒ a = -3
अतः a का अभीष्ट मान -3 है।

प्रश्न 9.
यदि बिन्दु (5, 1), (-2, -3) एवं (8, 2m) सरेखीय हों तो m का मान ज्ञात कीजिए।
हल :
चूँकि दिए हुए बिन्दु सरेखीय हैं अतः उससे बने क्षेत्र का क्षेत्रफल = 0 शून्य होगा।
⇒ \(\frac { 1 }{ 2 }\) [5 (-3 – 2m) + (-2) (2m – 1) + 8 (1 + 3)] = 0
⇒ – 15 – 10m – 4m + 2 + 32 = 0
⇒ – 14m + 19 = 0
⇒ 14m = +19
⇒ m = \(\frac { 19 }{ 14 }\)
अतः m का अभीष्ट मान = \(\frac { 19 }{ 14 }\) इकाई है।

प्रश्न 10.
यदि बिन्दु A (2, -4), बिन्दुओं P (3, 8) एवं Q (-10, v) से बराबर दूरी पर स्थित है, तो v का मान बताइए।
हल :
चूँकि AP = AQ दिया है
\(\sqrt{(2-3)^{2}+(-4-8)^{2}}=\sqrt{(2+10)^{2}+(-4-v)^{2}}\)
⇒ (-1)² + (- 12)² = (12)² + (-4 – v)² (दोनों ओर वर्ग करने पर)
⇒ 1 + 144 = 144 + 16 + v² + 8v
⇒ v² + 8v + 15 = 0
⇒ v² + 3v + 5v + 15 = 0
⇒ v(v + 3) + 5 (v + 3) = 0
⇒ (v + 3) (v+ 5) = 0
या तो v + 3 = 0 ⇒ v = -3
v + 5 = 0 ⇒ v = -5
अतः v के अभीष्ट मान = -3 अथवा -5 हैं।

प्रश्न 11.
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष (-8, 4), (-6, 6) एवं (-3, 9) हैं।
हल:
क्षेत्रफल = \(\frac { 1 }{ 2 }\) [-8 (6 – 9) + (-6) (9 – 4) + (-3) (4 – 6)]
= \(\frac { 1 }{ 2 }\) [-8 (-3) + (-6) (5) + (-3) (-2)]
= \(\frac { 1 }{ 2 }\) [24 – 30 + 6]
= \(\frac { 1 }{ 2 }\) [30 – 30]
= \(\frac { 1 }{ 2 }\) x 0
= 0
अतः त्रिभुज का अभीष्ट क्षेत्रफल = 0 है।

प्रश्न 12.
x-अक्ष, बिन्दुओं (-4,-6) एवं (-1, 7) को मिलाने वाले रेखाखण्ड को किस अनुपात में विभाजित करता है? उस छेदक बिन्दु के निर्देशांक भी ज्ञात कीजिए।
हल :
मान लीजिए x-अक्ष पर स्थित छेदक बिन्दु (x, 0) है तथा यह दी गयी रेखाखण्ड को m : 1 के अनुपात में विभाजित करता है तो
\(\frac{m(7)+1(-6)}{m+1}=0\)
7m – 6 = 0
m = \(\frac { 6 }{ 7 }\)
अत: x-अक्ष दिए रेखाखण्ड को 6 : 7 के अनुपात में विभाजित करता है।
अब

\(\frac { 1 }{ 2 }\)
अत: छेदक बिन्दु के अभीष्ट निर्देशांक (\(\frac { -34 }{ 13 }\), 0) हैं।

प्रश्न 13.
यदि P (9a – 2,- b) बिन्दुओं A (3a + 1, -3) एवं B (8a, 5) को मिलाने वाले रेखाखण्ड को 3 : 1 के अनुपात में अन्तः विभाजित करता है, तो a और b के मान ज्ञात कीजिए।
हल:

⇒ 36a – 8 = 27a + 1
⇒ 36a – 27a = 1 + 8
⇒ 9a = 9
⇒ a = \(\frac { 9 }{ 9 }\) = 1

⇒ b = -3
अतः a एवं b के अभीष्ट मान क्रमशः 1 एवं -3 हैं।

प्रश्न 14.
यदि (a, b), बिन्दुओं A (10, -6) एवं B (k, 4) को मिलाने वाले रेखाखण्ड का मध्य-बिन्दु है तथा a – 2b = 18 तोk का मान तथा AB दूरी ज्ञात कीजिए।
हल :
प्रश्नानुसार,

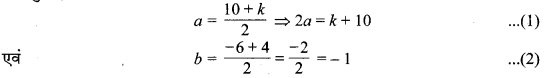
a – 2b = 18 (दिया है) …..(3)
a – 2 (-1) = 18
a = 16 ….(4) [समीकरण (2) एवं (3) से]
k + 10 = 2 x 16 = 32 [समीकरण (1) एवं (4) से]
k= 32 – 10 = 22
अतः k का अभीष्ट मान = 22 है।

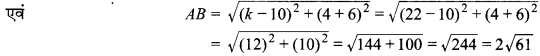
अत: AB का अभीष्ट मान = 2√61 इकाई है।

प्रश्न 15.
बिन्दुओं P (- 1, 3) एवं Q (2, 5) को मिलाने वाले रेखाखण्ड पर इस प्रकार स्थित बिन्दु R के निर्देशांक ज्ञात कीजिए कि PR = \(\frac { 3 }{ 5 }\) PQ.
हल :

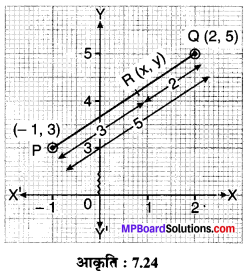
माना R के निर्देशांक (x, y) हैं और यह PQ को इस प्रकार विभाजित करता है कि PR : PQ = \(\frac { 3 }{ 5 }\)
PR : PQ = 3 : 5
PR : RQ = 3 : 2

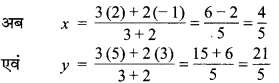
अतः बिन्दु R के अभीष्ट निर्देशांक \(\left(\frac{4}{5}, \frac{21}{5}\right)\) है।

MP Board Class 10th Maths Chapter 7 अति लघु उत्तरीय प्रश्न

[बताइए निम्न कथन सत्य हैं या असत्य अपने उत्तर का औचित्य भी दीजिए।

प्रश्न 1.
बिन्दु A (-1,0), B (3, 1), C (2, 2) एवं D (-2, 1) एक समान्तर चतुर्भुज के शीर्ष हैं।
हल :
कथन सत्य है, क्योंकि AC का मध्य-बिन्दु (\(\frac { 1 }{ 2 }\), 1) तथा BD का मध्य-बिन्दु भी (\(\frac { 1 }{ 2 }\), 1) है जो समान हैं तथा समान्तर चतुर्भुज के विकर्ण परस्पर समद्विभाजक होते हैं।

प्रश्न 2.
बिन्दु (4, 5), (7, 6) एवं (6, 3) संरेखीय हैं।
हल :
कथन असत्य है, क्योंकि बिन्दुओं से निर्मित त्रिभुजकार क्षेत्र का क्षेत्रफल
= \(\frac { 1 }{ 2 }\) [4 (6 – 3) + 7 (3 – 5) + 6 (5 – 6)]
= \(\frac { 1 }{ 2 }\) (12 – 14 – 6)
= – 4 ≠ 0.

प्रश्न 3.
बिन्दु P (0, – 7), y-अक्ष एवं बिन्दु A (-1, 0) तथा B (7, -6) को मिलाने वाले रेखाखण्ड के लम्ब अर्द्धक पर स्थित है।
हल :
कथन सत्य है, क्योंकि P (0, – 7) y-अक्ष पर है तथा

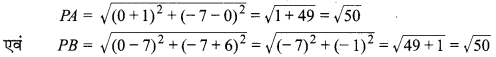
अर्थात् PA = PB जो AB के लम्ब समद्विभाजक पर स्थित है।

प्रश्न 4.
शीर्ष A (-2, 0), B (2, 0) एवं C (0, 2) वाला त्रिभुज ABC एवं शीर्ष D (-4,0), E (4,0) एवं F (0, 4) वाला त्रिभुज DEF समरूप हैं।
हल :
कथन सत्य है, क्योंकि तीनों संगत भुजाएँ समानुपाती हैं।

प्रश्न 5.
बिन्दु P(-4, 2), बिन्दुओं A (-4, 6) एवं B (-4, -6) को मिलाने वाले रेखाखण्ड पर स्थित हैं।
हल :
कथन सत्य है, क्योंकि तीनों बिन्दु x = – 4 रेखा पर स्थित हैं।

प्रश्न 6.
बिन्दु (0, 5), (0, – 9) एवं (3, 6) सरेखीय हैं।
हल :
कथन असत्य है, क्योंकि प्रथम दो बिन्दु }-अक्ष पर स्थित हैं जबकि तीसरा बिन्दु प्रथम चतुर्थांश में स्थित है।

प्रश्न 7.
बिन्दु P (0, 2), y-अक्ष एवं बिन्दु A (-1, 1) तथा B (3, 3) को मिलाने वाले रेखाखण्ड के लम्ब समद्विभाजक पर स्थित है।
हल :
कथन असत्य है, क्योंकि \(P A=\sqrt{(-1)^{2}+(-1)^{2}}=\sqrt{1+1}=\sqrt{2}\) एवं \(P B=\sqrt{(3)^{2}+(1)^{2}}\)
\(=\sqrt{9+1}=\sqrt{10}\) है अर्थात् PA ≠ PB.

प्रश्न 8.
बिन्दु A (3, 1), B (12, – 2) एवं C (0, 2) किसी त्रिभुज के शीर्ष नहीं हो सकते।
हल :
कथन सत्य है, क्योंकि ar (ABC) = \(\frac { 1 }{ 2 }\) [3 (-2 – 2) + 12 (2 – 1) + 0 (1 + 2)]
= \(\frac { 1 }{ 2 }\) [-12 + 12 + 0]
= 0.

प्रश्न 9.
बिन्दु A (4, 3), B (6, 4), C (5,-6) एवं D (-3, 5) किसी समान्तर चतुर्भुज के शीर्ष हैं।
हल :
कथन असत्य है, क्योंकि AC का मध्य-बिन्दु \(\left(\frac{9}{2},-\frac{3}{2}\right)\) तथा BD का मध्य-बिन्दु \(\left(\frac{3}{2}, \frac{9}{2}\right)\) है
अर्थात् विकर्ण परस्पर समद्विभाजित नहीं करते।

प्रश्न 10.
एक वृत्त का केन्द्र O मूलबिन्दु है। बिन्दु P (5, 0) इस पर स्थित है तथा बिन्दु Q(6, 8) वृत्त के बाहर स्थित है।
हल :
कथन सत्य है,क्योंकि OP = √(5)² = 5 एवं \(O Q=\sqrt{(6)^{2}+(8)^{2}}=\sqrt{36+64}=\sqrt{100}=10\) है
अर्थात् OQ > r (OP).

प्रश्न 11.
बिन्दु A (2, 7), बिन्दुओं P (6, 5) एवं Q (0, – 4) को मिलाने वाले रेखाखण्ड के लम्ब समद्विभाजक पर स्थित है।
हल :
कथन असत्य है क्योंकि \(A P=\sqrt{(4)^{2}+(-2)^{2}}=\sqrt{16+4}=\sqrt{20}\) एवं \(A Q=\sqrt{(2)^{2}+(11)^{2}}\) \(=\sqrt{4+121}=\sqrt{125}=5 \sqrt{5}\) अर्थात् AP ≠ AQ.

प्रश्न 12.
बिन्दु P (5, – 3), दो बिन्दुओं A (7, – 2) एवं B (1, – 5) को मिलाने वाले रेखाखण्ड को समत्रिभाजित करने वाले दो बिन्दुओं में से एक है।
हल :
कथन सत्य है, क्योंकि \(\frac{1(1)+2(7)}{1+2}=\frac{15}{3}=5\) एवं \(\frac{1(-5)+2(-2)}{1+2}=\frac{-5-4}{3}=\frac{-9}{3}\)
= – 3 अर्थात् बिन्दु P, AB को 1 : 2 के अनुपात में विभाजित करता है।

प्रश्न 13.
बिन्दु A (-6, 10), B (-4, 6) एवं C (3,-8) सरेखीय बिन्दु हैं इस प्रकार कि \(AB=\frac { 2 }{ 9 }AC\)
हल :
कथन सत्य है. क्योंकि

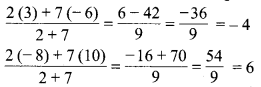
B, AC को 2 : 7 की अनुपात में विभाजित करता है। अर्थात् AB = \(\frac { 2 }{ 9 }\) AC.

प्रश्न 14.
बिन्दु P(-2, 4), त्रिज्या 6 एवं केन्द्र (3, 5) वाले वृत्त पर स्थित है।
हल :
कथन असत्य है, क्योंकि

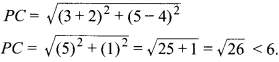
प्रश्न 15.
बिन्दु A (-1,- 2), B (4, 3), C (2, 5) एवं D (-3, 0) क्रम में एक आयत का निर्माण करते हैं।
हल :
कथन सत्य है, क्योंकि AC का मध्य-बिन्दु \(\left(\frac{1}{2}, \frac{3}{2}\right)\) एवं BD का मध्य-बिन्दु \(\left(\frac{1}{2}, \frac{3}{2}\right)\) है।

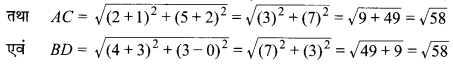
अर्थात् विकर्ण AC = BD = √58 एवं विकर्ण परस्पर बिन्दु \(\left(\frac{1}{2}, \frac{3}{2}\right)\) पर समद्विभाजित करते हैं।

MP Board Class 10th Maths Chapter 7 वस्तुनिष्ठ प्रश्न

MP Board Class 10th Maths Chapter 7 बहु-विकल्पीय प्रश्न

प्रश्न 1.
x-अक्ष से बिन्दु P (2, 3) की दूरी है :
(a) 2
(b) 3
(c) 1
(d) 5.
उत्तर:
(b) 3

प्रश्न 2.
बिन्दु A (0, 6) एवं B (0, – 2) के बीच दूरी है :
(a) 6
(b) 8
(c) 4
(d) 2.
उत्तर:
(b) 8

प्रश्न 3.
मूल बिन्दु से बिन्दु P(-6, 8) की दूरी है :
(a) 8
(b) 2√7
(c) 10
(d) 6.
उत्तर:
(c) 10

प्रश्न 4.
बिन्दु (0, 5) एवं (-5, 0) के बीच दूरी है :
(a) 5
(b) 5√2
(c) 2√5
(d) 10.
उत्तर:
(b) 5√2

प्रश्न 5.
AOBC एक आयत है जिसके तीन शीर्ष हैं A (0, 3), 0 (0, 0) एवं B (5,0); इसके विकर्ण की लम्बाई है:
(a) 5
(b) 3
(c) √34
(d) 4.
उत्तर:
(c) √34

प्रश्न 6.
त्रिभुज की परिमाप जिसके शीर्ष (0, 4), (0, 0) एवं (3, 0) हैं, है :
(a) 5
(b) 12
(c) 11
(d) 7 + √5.
उत्तर:
(b) 12

प्रश्न 7.
शीर्ष A (3,0), B (7,0) एवं C (8, 4) वाले त्रिभुज का क्षेत्रफल है :
(a) 14
(b) 28
(c) 8
(d) 6.
उत्तर:
(c) 8

प्रश्न 8.
बिन्दु (-4, 0), (4, 0) एवं (0, 3) शीर्ष हैं :
(a) समकोण त्रिभुज के
(b) सामद्विबाहु त्रिभुज के
(c) समबाहु त्रिभुज के
(d) विषमबाहु त्रिभुज के।
उत्तर:
(b) सामद्विबाहु त्रिभुज के

प्रश्न 9.
बिन्दु A (-2, -5) एवं B (2, 5) को मिलाने वाले रेखाखण्ड के लम्ब समद्विभाजक पर स्थित बिन्द
(a) (0,0)
(b) (0, 2)
(c) (2,0)
(d) (-2,0).
उत्तर:
(a) (0,0)

प्रश्न 10.
बिन्दुओं A (-2, 8) एवं B (-6,-4) को मिलाने वाले रेखाखण्ड का मध्य-बिन्दु है :
(a) (-4,-6)
(b) (2,6)
(c) (-4, 2)
(d) (4, 2).
उत्तर:
(c) (-4, 2)

रिक्त स्थानों की पूर्ति

1. किसी बिन्दु की y-अक्ष से दूरी ………. कहलाती है।
2. किसी बिन्दु की x-अक्ष से दूरी ……….. कहलाती है।
3. (0, y) एवं (x, 0) के मध्य दूरी ………… होती है।
4. (2a, 0) एवं (0, 2b) के मध्य-बिन्दु के निर्देशांक ……….. हैं।
5. तीन सरेखीय बिन्दुओं से बने त्रिभुज का क्षेत्रफल ………… है।
उत्तर-
1.x-निर्देशांक या भुज,
2. y-निर्देशांक या कोटि
3. \(\sqrt{x^{2}+y^{2}}\)
4. (a, b),
5. शून्य (0)।

जोड़ी मिलाइए

उत्तर-
1.→(c),
2.→(d),
3.→(e),
4.→(a),
5.→(b).

सत्य/असत्य कथन

1. (3, 0) एवं (0, 4) के बीच की दूरी 5 इकाई होती है।
2. (-4, 6) एवं (4,-6) के मध्य-बिन्दु के निर्देशांक (4, 6) हैं।
3. (4,0) एवं (0, 3) के बीच दूरी 5 इकाई है।
4. (0, 0), (3, 0), (0, 4) द्वारा बने त्रिभुज का क्षेत्रफल 12 इकाई है।
5. (x₁, y₁), (x₂, y₂), (x₃, y₃) शीर्ष वाले त्रिभुज के केन्द्रक के निर्देशांक \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\) है।
उत्तर-
1. सत्य,
2. असत्य,
3. सत्य,
4. असत्य,
5. सत्य।

एक शब्द/वाक्य में उत्तर

1. बिन्दु (x₁, y₁) एवं (x₂, y₂) के मध्य-बिन्दु के निर्देशांक लिखिए।
2. (x₁, y₁) एवं (x₂, y₂) के मध्य दूरी क्या होगी?
3. (x₁, y₁) एवं (x₂, y₂) को मिलाने वाली रेखा को m₁ : m₂ के अनुपात में अन्तः विभाजित करने वाले बिन्दु के निर्देशांक लिखिए।
4. बिन्दु (x₁, y₁), (x₂, y₂) एवं (x₃, y₃) से बने त्रिभुज का क्षेत्रफल लिखिए।
5. मूलबिन्दु से बिन्दु (x, y) के बीच दूरी क्या होगी?
उत्तर-